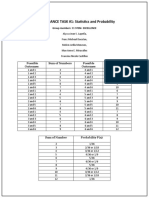
Chapter 3

Section 3.1 3.2 Pretest

Section 3.1-3.2 Pretest

1) A single six-sided die is rolled. Find the probability of rolling a seven.
A) 0.5
B) 0
C) 1
D) 0.1
B) 0
2) If one card is drawn from a standard deck of 52 playing cards, what is the
probability of drawing an ace?
A) 1/52
B) 1/13
C)
D) 1/2
B) 1/13
3) If an individual is selected at random, what is the probability that he or she
has a birthday in July? Ignore leap years.
A) 1/365
B) 31/365
C) 364/365
D) 12/365
B) 31/365

Section 3.1-3.2 Pretest

4) The distribution of blood types for 100 Americans is listed in the table. If one donor
is selected at random, find the probability of selecting a person with blood type A+.
Blood Type
Number
A) 0.68

O+
37

O6
B) 0.34

A+
34

A6

B+
10

B2

C) 0.4

AB+
4

AB1

D) 0.45

B) 0.34
5) Classify the statement as an example of classical probability, empirical probability,
or subjective probability. In California's Pick Three lottery, a person selects a 3-digit
number. The probability of winning California's Pick Three lottery is 1/1000.
A) subjective probability
B) classical probability

B) classical probability

C) empirical probability

Section 3.1-3.2 Pretest

6) Classify the statement as an example of classical probability, empirical probability,
or subjective probability. The probability that it will rain tomorrow is 24%.
A) classical probability

B) empirical probability

C) subjective probability

C) subjective probability
7) The P(A) = 3/5. Find the odds of winning an A.
A) 3:5

B) 5:2

C) 2:3

D) 3:2

D) 3:2
8) At the local racetrack, the favorite in a race has odds 3:2 of winning. What is the
probability that the favorite wins the race?
A) 0.2
B) 0.6

B) 0.6

C) 0.4

D) 1.5

Section 3.1-3.2 Pretest

9) Classify the events as dependent or independent. Events A and B where
P(A) = 0.7, P(B) = 0.8, and P(A and B) = 0.56
A) independent

B) dependent

B) dependent
10) Classify the events as dependent or independent. Event A: A red candy is
selected from a package with 30 colored candies and eaten. Event B: A blue candy
is selected from the same package and eaten.
A) dependent
A) dependent

B) independent

Section 3.1-3.2 Pretest

11) A group of students were asked if they carry a credit card. The responses are listed
in the table.
Class
Freshman
Sophomore
Total

Credit Card Carrier

46
32
78

Not a Credit Card

14
8
22

Carrier Total
60
40
100

If a student is selected at random, find the probability that he or she is a freshman

given that the student owns a credit card. Round your answers to three decimal
places.
A) 0.767

D) 0.590

B) 0.460

C) 0.410

D) 0.590

Section 3.1-3.2 Pretest

12) A group of students were asked if they carry a credit card. The responses are listed
in the table.
Class
Freshman
Sophomore
Total

Credit Card Carrier

14
17
31

Not a Credit Card

46
23
69

Carrier Total
60
40
100

If a student is selected at random, find the probability that he or she is a sophomore and
owns a credit card. Round your answers to three decimal places.
A) 0.452
C) 0.170

B) 0.548

C) 0.170

D) 0.775

Section 3.1-3.2 Pretest

13) You are dealt two cards successively without replacement from a standard deck
of 52 playing cards. Find the probability that the first card is a two and the second
card is a ten. Round your answer to three decimal places.
A) 0.994

B) 0.006

C) 0.500

D) 0.250

4 4
16

0.006
52 51 2652

B) 0.006
14) Find the probability that of 25 randomly selected students, no two share the same
birthday.
A) 0.431
B) 0.068
C) 0.569
D) 0.995
A) 0.431
P(different birthdays for all 25 students)

365 364 363 362 341

...
0.431
365 365 365 365 365

Section 3.1-3.2 Pretest

15) Use Bayes' theorem to solve this problem. A storeowner purchases stereos
from two companies. From Company A, 250 stereos are purchased and 1% are
found to be defective. From Company B, 950 stereos are purchased and 10% are
found to be defective. Given that a stereo is defective, find the probability that it
came from Company A.
A) 1/39

B) 10/39

C) 38/39

A) 1/39

P( A \ B)

250
250
1

; P( B \ A)
250 950 1200
100
950
950
10
P( A ')

; P ( B \ A ')
250 950 1200
100
P( A)

250
1

250
1
1200 100
P( A \ B)

250
1
950 10 9750 39

1200 100 1200 100

D) 19/195

P ( A) P (B\ A)
P( A) P ( B \ A) P(A') P(B\ A')

Section 3.1-3.2 Pretest

16) Use the following graph, which shows the types of incidents encountered with
drivers using cell phones, to find the probability that a randomly chosen incident
involves cutting off a car. Round your answer to three decimal places.
0.163

Section 3.1-3.2 Pretest

17) Identify the sample space of the probability experiment: recording the number
of days it snowed in Cleveland in the month of January.
0, 1, 2, 3, 4, 5, 31
18) Identify the sample space of the probability experiment: determining the
children's gender for a family of three children (Use B for boy and G for girl.)
(BBB), (BBG), (BGB), (GBB), (BGG), (GBG), (GGB), (GGG)
19) Identify the sample space of the probability experiment: recording the day of the
week and whether or not it rains.
MR, TUR, WEDR, THR, FRR, SATR, SUNR, MN, TUN, WEDN, THN, FRN, SATN,
SUNN

Section 3.1-3.2 Pretest

20) Find the probability of selecting two consecutive threes when two cards are
drawn without replacement from a standard deck of 52 playing cards. Round your
answer to four decimal places.
P(2-threes) = (4/52)(3/51)= 0.0045
21) A multiple-choice test has five questions, each with five choices for the answer.
Only one of the choices is correct. You randomly guess the answer to each question.
What is the probability that you answer at least one of the questions correctly?
P(at least one correct) = 1 P(all five answers incorrect)
= 1 (4/5)(4/5)(4/5)(4/5)(4/5)
= 1 0.32768 = 0.67232