Professional Documents
Culture Documents
ME 3230 Chapter 9 Spatial Modeling
Uploaded by
Jackie YipCopyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
ME 3230 Chapter 9 Spatial Modeling
Uploaded by
Jackie YipCopyright:
Available Formats
1
Lecture Slides
ME 3230 Kinematics and Mechatronics
Chapter 9
Spatial Modeling some fundamentals
for Robot Kinematics
By Dr. Debao Zhou
2
Scope and Covered Materials
Scope
Rotation and homogenous transformation in 3D space
Properties of rotation and homogenous transformation
matrix
Forward kinematics
Denavit - Hartenberg Method (D-H Method)
Inverse kinematics
Reading materials:
Corresponding materials in Spong and Vidyasagars book,
Chapters 2, 3 and 4.
Sciavicco and Siciliano : Sections 2.1-2.4, 2.7-2.9 and 2.12
Corresponding materials in our Text book
3
3D Robot Manipulator
Robot Hand Position and Orientation Expression
4
P(x, y, z, o, |, )
Rigid body - frame/vector
Frame position, orientation
- relative to difference frames
Vector position, orientation
- relative to difference frames
5
3D Vector Expressed in Different Frames
Vector r
P/O
is expressed as p
0
in frame
ox
0
y
0
z
0
and p
1
in frame ox
1
y
1
z
1
. The i, j, k
are the corresponding unit vectors
1 frame to 0 frame from matrix rotation the is
1
0
R
6
3D Vector Expressed in Different Frames
7
Example #1:
Rotation u around z
1
/z
0
(positive u from frame 0
to frame 1)
Next page: Several examples: i, j, k expressed in 1 to expressed in 0
8
Example #1:
Rotation u around z
1
/z
0
(positive u from 0 to 1)
Meaning? Transform a vector
expression in Frame 1 to frame 0
0
0
1
1 0 0
0 cos sin
0 sin cos
0
sin
cos
1
1
0 0
p R p =
(
(
(
(
(
(
=
(
(
(
u u
u u
u
u
0
1
0
1 0 0
0 cos sin
0 sin cos
0
cos
sin
1
1
0 0
p R p =
(
(
(
(
(
(
=
(
(
(
u u
u u
u
u
Explain u = 90, 180, 270
9
Three Simple rotations
Similarly, rotation u around x
0
, y
0
or z
0
axis
(
(
(
u u
u u
=
u
1 0 0
0 cos sin
0 sin cos
R
, z
Physical Meaning R
0
1
Frames #0 and #1 share the same origin;
R
0
1
means the transformation of a vector
expressed in frame #1 to the expression in
frame #0 by using the rotation angle from
frame #0 to #1;
R
m
n
means the transformation of a vector
expressed in frame #n to the expression in
frame #m by using the rotation angle from
frame #m to #n.
10
Multiple Rotations
p
0
= R
0
1
p
1
p
1
= R
1
2
p
2
So
p
0
= R
0
1
R
1
2
p
2
And
p
0
= R
0
2
p
2
Thus
R
0
2
= R
0
1
R
1
2
and R
0
2
(R
0
2
)
T
= 1
11
1
2
3
12
Properties of Rotation Matrix
Transposition:
Inversion:
Multiple multiplications
Any rotation matrix is Orthogonal Matrices
( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) | |
( )
I
R R
R R R R R R R R
R R R R R R R
R R R R R R R R
n
n
T
n
n
n
n
T T T T
n
n
n
n
T T T T
n
n
n
n
T n
n
=
=
=
=
1 1
1
3
2
2
1
1
0
1
0
2
1
3
2 1
1
3
2
2
1
1
0
2
1
3
2 1
1
3
2
2
1
1
0 1
3
2
2
1
1
0
) (
) (
) ( ) (
( ) ( )
1
0 0
0
1
3
2
2
1
1
0 0
is There
Set
= =
=
n
T
n
n
n
n
n
R R R
R R R R R
13
Composition of Rotation Matrices
Matrix product is not commutative
Two rotations in general do not commute and its
composition depends on the order of the single rotations.
Mathematically, AB = BA
Or R
0
1
R
1
2
= R
1
2
R
0
1
.
( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) | |
( )
I
R R
R R R R R R R R
R R R R R R R
R R R R R R R R
n
n
T
n
n
n
n
T T T T
n
n
n
n
T T T T
n
n
n
n
T n
n
=
=
=
=
1 1
1
3
2
2
1
1
0
1
0
2
1
3
2 1
1
3
2
2
1
1
0
2
1
3
2 1
1
3
2
2
1
1
0 1
3
2
2
1
1
0
) (
) (
) ( ) (
Continues Rotation
Continues rotation
around the current
frame
Body-fixed frame
rotation
Continues rotation
around a fixed
frame
World-fixed frame
rotation
14
Continues Rotation: Euler Angle
Body Fixed Rotation
Leonhard Euler to describe the orientation of a rigid body
in 3D space
Any orientation can be described by three consequence
rotations
15
16
Continues Rotation - Euler Angles - YXZ
Rot(Y,
1
) Rot(X,
2
) Rot(Z,
3
)
Table of Rotation Matrix Euler Anlges
17
Homogeneous Transformation
Frames do not share the same origin!
18
| |
(
=
(
=
(
+
=
(
=
(
=
(
=
(
=
(
=
(
1 1
1 1 0
1 1 1 0 1
1 1 1 0 1
1 1
2
2 2
0
2
2 2
1
1
0
2
2
0
0 / 1
1
1 / 2
0
1
1
2
0
1
1
1 1
0
1
1
0
0 / 1
1
0
0
0
2
2 2
1
2
2
1
1 / 2
2
1
1
1
2 2 2
2
2
p p
p r r R R R
p p r R p
p p r R p
z y x p
T
H H H
H
H
19
Homogeneous Transformation
| |
T
z y x p
2 2 2
2
2
=
=
=
(
=
(
1
1
1
3 3
1
1 3 1
3 1
0
H
H
0
H
0
H
d R R
d
R
d R
T T
T
T
T
2
2
p
1
1
p
0
0
p
0
0 / 1
r
1
1 / 2
r
P
1
1 / 2
2
2
2
1
1
1 / 2
2
2
1
1
r p R r p p
+ = + =
0
0 / 1
1
1
1
0
0
0 / 1
1
1
0
0
r p R r p p
+ = + =
( )
0
0 / 1
1
1 / 2
2
2
1
2
1
0
r r p R R
+ + =
0
0 / 1
1
1 / 2
1
0
2
2
2
1
1
0
r r R p R R
+ + =
2
2
p
1
1
p
0
0
p
0
0 / 1
r
1
1 / 2
r
P
20
What is the benefit to us?
Robot manipulator express the end-effector
vector to the base frame. Fundamentally
different from those in Chapter 5
2
2
p
1
1
p
0
0
p
0
0 / 1
r
1
1 / 2
r
21
Basic Homogeneous Transformation
Translation
Simple Rotation
22
Defining the Homogeneous Transformation Matrix
It is a 4x4 Matrix that describes 3-Space with
information that relates Orientation and Position (pose) of
a remote space to a local space
n
x
o
x
a
x
d
x
n
y
o
y
a
y
d
y
n
z
o
z
a
z
d
z
0 0 0 1
n vector
projects the
X
rem
Axis to the
Local
Coordinate
System
o vector
projects
the Y
rem
Axis to the
Local
Coordinate
System
a vector
projects the
Z
rem
Axis to
the Local
Coordinate
System
d vector is
the position
of the origin
of the
remote
space in
Local
Coordinate
dimensions
This 3x3 Sub-Matrix is
the information that
relates orientation of
Frame
rem
to Frame
Local
(This is called R the
rotational Submatrix)
(
=
(
=
(
=
(
=
(
1 1 1 0 1
1 1 1 0 1
1
1 1
0
1
1
0
0 / 1
1
0
0
0
2
2 2
1
2
2
1
1 / 2
2
1
1
1
p p r R p
p p r R p
H
H
2
2
p
1
1
p
0
0
p
0
0 / 1
r
1
1 / 2
r
P
23
Defining the Homogeneous Transformation Matrix
n
x
o
x
a
x
d
x
n
y
o
y
a
y
d
y
n
z
o
z
a
z
d
z
0 0 0 1
Perspective
or Projection
Vector
Scaling
Factor
This matrix is a transformation
tool for space motion!
24
HTM A Physical Interpretation
1. A representation of a coordinate transformation
relating the coordinates of a point P between 2
different coordinate systems
2. A representation of the position and orientation
(pose) of a transformed coordinate frame in the
space defined by a fixed coordinate frame
3. An operation that takes a
vector P and rotates
and/or translates it to a
new vector P
t
in the same
coordinate frame
2
2
p
1
1
p
0
0
p
0
0 / 1
r
1
1 / 2
r
P
(
=
(
=
(
1 1 1 0 1
1
1 1
0
1
1
0
0 / 1
1
0
0
0
p p r R p
H
(
=
1 0
0
0 / 1
1
0 1
0
r R
H
25
Looking Closely at the T
0
n
Matrix
T
0
n
matrix related the
end of the arm frame
(n) to its base (0)
Thus it must contain
information related to
the several joints of the
robot
It is a 4x4 matrix
populated by complex
equations for both
position and orientation
(POSE)
26
Looking Closely at the T
0
n
Matrix
To get at the equation set, we
will choose to add a series of
coordinate frames to each of
the joint positions
There are n+1 frames
n+1 rigid bodies = number of
frames Why?
n joints
The frame attached to the 1
st
joint
is labeled 0 the base frame!
while joint two has Frame 1, etc.
The last Frame is the end or n
Frame
27
Looking Closely at the T
0
n
Matrix
As we have seen earlier, we
can define a HTM (T
(i-1)
i
) to the
transformation between any
two consecutive frames
Thus we will find that the T
0
n
is
given by a product formed by:
n
n
n
T T T T
1
2
1
1
0 0
=
28
Looking Closely at the T
0
n
Matrix
For simplicity, we will redefine
each of the of these transforms
(T
(i-1)
i
) as A
i
Then, for a typical 3 DOF robot
Arm,
T
0
3
= A
1
*A
2
*A
3
While for a full functioned 6 DOF
robot (arm and wrist) would be:
T
0
n
= A
1
*A
2
*A
3
*A
4
*A
5
*A
6
A
1
to A
3
explain the arm joint
effect while A
4
to A
6
explain the
wrist joint effects
29
Frame To Frame Arrangements in 3D Space
When we move from one frame to another,
we will encounter:
Two translations (in a controlled sense)
Two rotations (also in a controlled sense)
A rotation and translation WRT the Z
i-1
These are called the Joint Parameters
A rotation and translation WRT the X
i
These are called the Link Parameters
30
Relationship between Two Frames
Rotate u around z
i-1
, translate d along z
i-1
, translate a
along x
i
axis, and rotate o around x
i
axis.
Frame (i-1) on link (i-1)
Frame i on link i
31
Talking Specifics Joint Parameters
u
i
is an angle measured about the Z
i-1
axis
from X
i-1
to X
i
and is a variable for a
revolute joint its fixed for a Prismatic Joint
d
i
is a distance measured from the origin of
Frame
(i-1)
to the intersection of Z
i-1
and X
i
and is a variable for a prismatic joint its
fixed for a Revolute Joint
32
Talking Specifics Link Parameters
a
i
is the Link length and measures the distance
from the intersection of Z
i-1
to the origin of Frame
i
measured along X
i
o
i
is the Twist angle which measures the angle
from Z
i-1
to Z
i
as measured about X
i
Both of these parameters are fixed in value
regardless of the joint type.
A Further note: Fixed does not mean zero degrees or
zero length just that they dont change
33
34
Returning to the 4 Frame-Pair Operators:
1
st
is u which is an
operation of pure
rotation about Z or:
2
nd
is d which is a
translation along Z or:
os 0 0
0 0
0 0 1 0
0 0 0 1
C Sin
Sin Cos
u u
u u
(
(
(
(
(
1 0 0 0
0 1 0 0
0 0 1
0 0 0 1
d
(
(
(
(
(
35
Returning to the 4 Frame Operators:
3
rd
is a Translation
Along X or:
4
th
is o which is a
pure Rotation
about X or:
1 0 0
0 1 0 0
0 0 1 0
0 0 0 1
a
(
(
(
(
(
1 0 0 0
0 0
0 0
0 0 0 1
Cos Sin
Sin Cos
o o
o o
(
(
(
(
(
36
The Overall Effect is:
os 0 0 1 0 0 0 1 0 0 1 0 0 0
0 0 0 1 0 0 0 1 0 0 0 0
0 0 1 0 0 0 1 0 0 1 0 0 0
0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1
C Sin a
Sin Cos Cos Sin
d Sin Cos
u u
u u o o
o o
( ( ( (
( ( ( (
( ( ( (
- - -
( ( ( (
( ( ( (
o u , , , , 1 x a x d z z i
i
i
Rot Tran Tran Rot A T = =
37
Simplifying this Matrix Product:
0
0 0 0 1
i i i i i i i
i i i i i i i
i i i
C S C S S a C
S C C C S a S
S C d
u u o u o u
u u o u o u
o o
- - -
(
(
- - -
(
(
(
This matrix is the general transformation relating each
and every of the frame pairs along a robot structure
o u , , , , 1 x a x d z z i
i
i
Rot Tran Tran Rot A T = =
38
Mathematica Code
39
Mathematica Code
40
Robot Kinematics
Foreword Kinematics
Definition: Given the joint variable of the robot ,
to determine the position and orientation of the
end-effector.
Inverse Kinematics
Definition: Given a desired position and
orientation of the end-effector of a robot,
determine a set of joint variables that achieve
the desired position and orientation.
41
Denavit-Hartenberg Method
or D-H Convention
A Step-by-Step approach for modeling each of the
frames from the initial (or 0) frame all the way to the n
(or end) frame
This modeling technique
makes each joint axis
(either rotation or translation)
the Z-axis of the appropriate
frame (Z
0
to Z
n-1
).
The Joint motion, thus, is taken
W.R.T. the Z
i-1
axis of the frame
pair making up the specific transformation matrix
under design
42
Foreword Kinematics Direct Kinematics
43
Applying D-H to a General Case:
Link i:
Connect frame i-1 and frame i
Connect joint i and joint i+1
Think: Link i -1 as the
ground link (or link 0):
- Joint 1 and frame 0
Denavit-Hartenberg Reference Frame Layout
http://www.youtube.com/watch?v=rA9tm0g
Tln8
44
45
The D-H Modeling Rules:
1) Locate and mark the
motion ( using u
i
and d
i
)
and label the joint axes:
Z
0
to Z
n-1
2) Establish the Base
Frame. Set Base Origin
anywhere on the Z
0
axis. Choose X
0
and Y
0
conveniently and to
form a right hand frame.
0) Identify links and joints (motions)
n+1 links from 0 to n, n joints for n+1 links;
46
The D-H Modeling Rules:
3) Locate the origin O
i
where the common
normal to Z
i-1
and Z
i
intersects Z
i
. If Z
i
intersects Z
i-1
locate O
i
at
this intersection. If Z
i-1
and Z
i
are parallel, locate
O
i
at Joint i+1
Or X
i
has to be perpendicular
with Z
i
and Z
i-1
and
connect with Z
i
and Z
i-1
The intersection points forms
the origin of the frames
n+1 links from 0 to n, n joint from 0 to n-1;
47
The D-H Modeling Rules:
4) Establish X
i
along the common normal
between Z
i-1
and Z
i
through O
i
, or in the
direction Normal to the plane Z
i-1
Z
i
if
these axes intersect
5) Establish Y
i
to form a right hand system
Set i = i+1, if i<n loop back to step 3
(Repeat Steps 3 to 5 for i = 1 to i = n-1)
48
The D-H Modeling Rules:
6) Establish the End-Effector (n) frame:
O
n
X
n
Y
n
Z
n
. Assuming the n
th
joint is
revolute, set k
n
= a along the direction Z
n-1
.
Establish the origin O
n
conveniently along
Z
n
, typically mounting point of gripper or
tool. Set j
n
= o in the direction of gripper
closure (opening) and set i
n
= n such that n
= oxa. Note if tool is not a simple gripper,
set X
n
and Y
n
conveniently to form a right
hand frame.
49
The D-H Modeling Rules:
7) Create a table of Link parameters:
1) u
i
as angle about Z
i-1
between Xs
2) d
i
as distance along Z
i-1
3) o
i
as angle about X
i
between Zs
4) a
i
as distance along X
i
8) Form HTM matrices A
1
, A
2
, A
n
by
substituting u, d, o and a into the general
model
9) Form T
0
n
= A
1
*A
2
**A
n
50
Some Issues to remember:
X
i
is perpendicular with Z
i-1
and intersect with Z
i-1
.
X axis
If you have parallel Z axes, the X axis of the second
frame runs perpendicularly between them
Kinematic Home
When working on a revolute joint, the model will be
simpler if the two X directions are in alignment at
Kinematic Home i.e. Our models starting point (u =
0)
To achieve this kinematic home, rotate the model about
moveable axes (Z
i-1
s) to align Xs or set u = 0
Kinematic Home is not particularly critical for prismatic
joints
51
Some Issues to remember:
An ideal model will have n+1 frames
However, additional frames may be
necessary these are considered Dummy
frames since they wont contain joint axes
52
Three-link Planar Arm
53
Three-link Planar Arm
Individual Homogenous Transformation
Matrix
Homogenous Transformation Matrix from 0
to 3
T
0
3
= A
1
A
2
A
3
=
2-DOFs (Motions)
54
x
0
y
0
x
1
z
1
z
2
x
2
u
d
u
55
Example 1: 6-dofs Articulating Arm
56
D-H Table
Frames Link Var u d a o So Co Su Cu
0 to1 1 R u
1
0 0 90 -1 0 S1 C1
1 to2 2 R u
2
0 a
2
0 0 1 S2 C2
2 to 3 3 R u
3
0 a
3
0 0 1 S3 C3
3 to 4 4 R u
4
0 a
4
-90 -1 0 S4 C4
4 to 5 5 R u
5
0 0 90 1 0 S5 C5
5 to 6 6 R u
6
*
d
6
0 0 0 1 S6 C6
* With End Frame in Better Kinematic Home. Here,
as shown, it would be (o
6
- 90), which is a problem!
57
A Matrices
1
1 0 1 0
1 0 1 0
0 1 0 0
0 0 0 1
C S
S C
A
(
(
(
=
(
(
2
2
2
2 2 0 2
2 2 0 2
0 0 1 0
0 0 0 1
C S a C
S C a S
A
-
(
(
-
(
=
(
(
3
3
3
3 3 0 3
3 3 0 3
0 0 1 0
0 0 0 1
C S a C
S C a S
A
-
(
(
-
(
=
(
(
4
4
4
4 0 4 4
4 0 4 4
0 1 0 0
0 0 0 1
C S a C
S C a S
A
-
(
(
-
(
=
(
(
58
A Matrices, cont.
5
5 0 5 0
5 0 5 0
0 1 0 0
0 0 0 1
C S
S C
A
(
(
(
=
(
(
6
6
6 6 0 0
6 6 0 0
0 0 1
0 0 0 1
C S
S C
A
d
(
(
(
=
(
(
At Better Kinematic Home!
59
Leads To:
Forward Kinematics is
After Preprocessing A2-A3-A4,
with (Full) Simplify function, the
FKS must be reordered as A1-
A
234
-A5-A6 and Simplified
6
5
2
1
1
0
6
0
T T T T =
60
Solving for FKS
Pre-process {A
2
*A
3
*A
4
} with Full Simplify
They are the planer arm issue as in the
previous robot model
Then Form: A
1
* {A
2
*A
3
*A
4
}*A
5
*A
6
Simplify for FKS!
61
Simplifies to (in the expected Tabular Form):
nx = C1(C5C6C234 - S6S234) - S1S5C6
ny = C1S5C6 + S1(C5C6C234 - S6S234)
nz = S6C234 + C5C6S234
ox = S1S5S6 - C1(C5S6C234 + C6S234)
oy = - C1S5S6 - S1(C5S6C234 + C6S234)
oz = C6C234 - C5S6S234
ax = C1S5C234 + S1C5
ay = S1S5C234 - C1C5
az = S5S234
dx = C1(C234(d6S5 + a4) + a3C23 + a2C2) + d6S1C5
dy = S1(C234(d6S5 + a4) + a3C23 + a2C2) - d6C1C5
dz = S234(d6S5 + a4) + a3S23 + a2S2
62
Verify the Model
Again, substitute knowns (typically 0 or 0
units) for the variable kinematic variables
Check each individual A matrix against
your robot frame skeleton sketch for
physical agreement
Check the simplified FKS against the
Frame skeleton for appropriateness
63
After Substitution:
nx = C1(C5C6C234 - S6S234) - S1S5C6 = 1(1-0) 0 = 1
ny = C1S5C6 + S1(C5C6C234 - S6S234) = 0+ 0(1 0) = 0
nz = S6C234 + C5C6S234 = 0 + 0 = 0
ox = S1S5S6 - C1(C5S6C234 + C6S234) = 0 1(0 + 0) = 0
oy = - C1S5S6 - S1(C5S6C234 + C6S234) = -0 0(0 + 0) = 0
oz = C6C234 - C5S6S234 = 1 0 = 1
ax = C1S5C234 + S1C5 = 0 + 0 = 0
ay = S1S5C234 - C1C5 = 0 1 = -1
az = S5S234 = 0
dx = C1(C234(d6S5 + a4) + a3C23 + a2C2) + d6S1C5
= 1*(1(0 + a4) + a3 + a2) + 0 = a4 + a3 + a2
dy = S1(C234(d6S5 + a4) + a3C23 + a2C2) - d6C1C5
= 0(1(0 + a4) + a3 + a2) d6 = -d6
dz = S234(d6S5 + a4) + a3S23 + a2S2
= 0(0 + a4) + 0 + 0 = 0
64
Inverse Kinematics
Based on the direct (forward) kinematics
and the special properties of HTM
properties to calculate the joint parameters
(angle for revolute joint and moving
distance for prismatic joint)
You might also like
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeFrom EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeRating: 4 out of 5 stars4/5 (5794)
- The Little Book of Hygge: Danish Secrets to Happy LivingFrom EverandThe Little Book of Hygge: Danish Secrets to Happy LivingRating: 3.5 out of 5 stars3.5/5 (399)
- Hello This Is A Message Regarding The Use of The Instantaneous VelocityDocument1 pageHello This Is A Message Regarding The Use of The Instantaneous VelocityJackie YipNo ratings yet
- Hello This Is A Message Regarding The Use of The Integration SystemDocument1 pageHello This Is A Message Regarding The Use of The Integration SystemJackie YipNo ratings yet
- Hello This Is A Message Regarding The Use of The IphoneDocument1 pageHello This Is A Message Regarding The Use of The IphoneJackie YipNo ratings yet
- Hello This Is A Message Regarding The Use of The Dell PCDocument1 pageHello This Is A Message Regarding The Use of The Dell PCJackie YipNo ratings yet
- Flappy BirdDocument1 pageFlappy BirdJackie YipNo ratings yet
- Hello This Is A Message Regarding The Use of The LG Optimus GDocument1 pageHello This Is A Message Regarding The Use of The LG Optimus GJackie YipNo ratings yet
- Hello This Is A Message Regarding The Use of The Formula SAE CarDocument1 pageHello This Is A Message Regarding The Use of The Formula SAE CarJackie YipNo ratings yet
- Hello This Is A Message Regarding The Use of The PID Control SystemDocument1 pageHello This Is A Message Regarding The Use of The PID Control SystemJackie YipNo ratings yet
- Hello This Is A Message Regarding The Use of The League of Legends GameDocument1 pageHello This Is A Message Regarding The Use of The League of Legends GameJackie YipNo ratings yet
- Hello This Is A Message Regarding The Use of The Country ChinaDocument1 pageHello This Is A Message Regarding The Use of The Country ChinaJackie YipNo ratings yet
- Hello This Is A Message Regarding The Use of The ANSYS FluentDocument1 pageHello This Is A Message Regarding The Use of The ANSYS FluentJackie YipNo ratings yet
- Hello This Is A Message Regarding The Use of The Xbox 360Document1 pageHello This Is A Message Regarding The Use of The Xbox 360Jackie YipNo ratings yet
- Art Today - Visit TwoDocument1 pageArt Today - Visit TwoJackie YipNo ratings yet
- Hello This Is A Message Regarding The Use of The LG Optimus GDocument1 pageHello This Is A Message Regarding The Use of The LG Optimus GJackie YipNo ratings yet
- EMGT 4110 Week1 Thursday Lecture1Document21 pagesEMGT 4110 Week1 Thursday Lecture1Jackie YipNo ratings yet
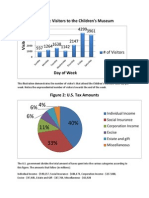
- Children's Museum Visitor Numbers and US Tax Amounts by CategoryDocument2 pagesChildren's Museum Visitor Numbers and US Tax Amounts by CategoryJackie YipNo ratings yet
- MasterCAM For SolidWorksDocument62 pagesMasterCAM For SolidWorksJackie YipNo ratings yet
- Children's Museum Visitor Numbers and US Tax Amounts by CategoryDocument2 pagesChildren's Museum Visitor Numbers and US Tax Amounts by CategoryJackie YipNo ratings yet
- Sand Cast HREDocument1 pageSand Cast HREJackie YipNo ratings yet
- Jackie Yip - Fluid Mechanics CalculationsDocument5 pagesJackie Yip - Fluid Mechanics CalculationsJackie YipNo ratings yet
- Series VSC (Obsolete)Document48 pagesSeries VSC (Obsolete)Jackie YipNo ratings yet
- ME3230 Syllabus DzhouDocument4 pagesME3230 Syllabus DzhouJackie YipNo ratings yet
- US6755258B1Document21 pagesUS6755258B1Jackie YipNo ratings yet
- ME 3230 Chapter 6 Plannar Linkage Design - 1Document59 pagesME 3230 Chapter 6 Plannar Linkage Design - 1Jackie YipNo ratings yet
- Engineering drawing dimensions chartDocument1 pageEngineering drawing dimensions chartAmra Talić-ČikmišNo ratings yet
- Final SolutionsDocument6 pagesFinal SolutionsJackie YipNo ratings yet
- ME 4145 Lab3 AsignmentDocument3 pagesME 4145 Lab3 AsignmentJackie YipNo ratings yet
- Samp 2Document1 pageSamp 2Jackie YipNo ratings yet
- Samp 2Document1 pageSamp 2Jackie YipNo ratings yet
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryFrom EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryRating: 3.5 out of 5 stars3.5/5 (231)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceFrom EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceRating: 4 out of 5 stars4/5 (894)
- The Yellow House: A Memoir (2019 National Book Award Winner)From EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Rating: 4 out of 5 stars4/5 (98)
- Shoe Dog: A Memoir by the Creator of NikeFrom EverandShoe Dog: A Memoir by the Creator of NikeRating: 4.5 out of 5 stars4.5/5 (537)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureFrom EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureRating: 4.5 out of 5 stars4.5/5 (474)
- Never Split the Difference: Negotiating As If Your Life Depended On ItFrom EverandNever Split the Difference: Negotiating As If Your Life Depended On ItRating: 4.5 out of 5 stars4.5/5 (838)
- Grit: The Power of Passion and PerseveranceFrom EverandGrit: The Power of Passion and PerseveranceRating: 4 out of 5 stars4/5 (587)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaFrom EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaRating: 4.5 out of 5 stars4.5/5 (265)
- The Emperor of All Maladies: A Biography of CancerFrom EverandThe Emperor of All Maladies: A Biography of CancerRating: 4.5 out of 5 stars4.5/5 (271)
- On Fire: The (Burning) Case for a Green New DealFrom EverandOn Fire: The (Burning) Case for a Green New DealRating: 4 out of 5 stars4/5 (73)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersFrom EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersRating: 4.5 out of 5 stars4.5/5 (344)
- Team of Rivals: The Political Genius of Abraham LincolnFrom EverandTeam of Rivals: The Political Genius of Abraham LincolnRating: 4.5 out of 5 stars4.5/5 (234)
- The Unwinding: An Inner History of the New AmericaFrom EverandThe Unwinding: An Inner History of the New AmericaRating: 4 out of 5 stars4/5 (45)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyFrom EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyRating: 3.5 out of 5 stars3.5/5 (2219)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreFrom EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreRating: 4 out of 5 stars4/5 (1090)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)From EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Rating: 4.5 out of 5 stars4.5/5 (119)
- Her Body and Other Parties: StoriesFrom EverandHer Body and Other Parties: StoriesRating: 4 out of 5 stars4/5 (821)
- Arapura, Introduction To Differential FormsDocument30 pagesArapura, Introduction To Differential FormsΣωτήρης ΝτελήςNo ratings yet
- Polar Coordinates NotesDocument15 pagesPolar Coordinates NotesEnzo OoiNo ratings yet
- Calculus II Course Notes (Traces of Surfaces)Document6 pagesCalculus II Course Notes (Traces of Surfaces)Emil James LadoresNo ratings yet
- Circle CompositesDocument89 pagesCircle Compositesshashikesh kumarNo ratings yet
- Moment of Inertia and Radius of Gyration ExplainedDocument12 pagesMoment of Inertia and Radius of Gyration ExplainedVivo 1906No ratings yet
- CDI 63: Advanced Surfacing in Solidworks: Documentation Package ForDocument17 pagesCDI 63: Advanced Surfacing in Solidworks: Documentation Package ForGaurav GuptaNo ratings yet
- Chari PressleyDocument31 pagesChari Pressleylandvermesser110No ratings yet
- Core and Cavity ExtractionDocument129 pagesCore and Cavity ExtractionSaggam Narasimharaju100% (1)
- Gauge TheoryDocument7 pagesGauge TheoryEli GerberNo ratings yet
- Introduction and Vector AlgebraDocument166 pagesIntroduction and Vector Algebra357911No ratings yet
- Solved Problems From Hibbelers Book Engineering Mechanics - SECTIONS 12-9 AND 12-10Document21 pagesSolved Problems From Hibbelers Book Engineering Mechanics - SECTIONS 12-9 AND 12-10Sai PavanNo ratings yet
- Maths EM Glance Me Once 2022Document49 pagesMaths EM Glance Me Once 2022manjulla raju0% (1)
- Handout1 - Laplacian OperatorDocument5 pagesHandout1 - Laplacian OperatorAkkapanthula Sai HaranadhNo ratings yet
- Kikoin, Kikoin - Senior Physics 1Document254 pagesKikoin, Kikoin - Senior Physics 1Sashank VarmaNo ratings yet
- Class 7 Cbse Maths Sample Paper Term 2 Model 1Document4 pagesClass 7 Cbse Maths Sample Paper Term 2 Model 1Sunaina RawatNo ratings yet
- Melted Ice Cream Cone Ratio PuzzleDocument3 pagesMelted Ice Cream Cone Ratio PuzzleJm CerrudoNo ratings yet
- C3 Modulus Functions PDFDocument5 pagesC3 Modulus Functions PDFatul kumarNo ratings yet
- 3ds Max 2016 Help - About The Edit Normals ModifierDocument4 pages3ds Max 2016 Help - About The Edit Normals Modifierpulkit sharmaNo ratings yet
- Solve Quadratic EquationsDocument4 pagesSolve Quadratic EquationsVan Gile EcleoNo ratings yet
- Maths CHP 6Document25 pagesMaths CHP 6shishir jhaNo ratings yet
- SohcahtoaDocument18 pagesSohcahtoaASHWANI Raj100% (1)
- Fifi and Christian Buy Some Land InvestigationDocument10 pagesFifi and Christian Buy Some Land InvestigationJIAYI XU0% (1)
- Lesson 19: Related Rates Worksheet SolutionsDocument3 pagesLesson 19: Related Rates Worksheet SolutionsMatthew Leingang100% (5)
- Wisegot: Federal Physics 11Th Solved Excercises McqsDocument11 pagesWisegot: Federal Physics 11Th Solved Excercises McqsFakhar DinNo ratings yet
- UT (A) - CoE (XI) - Test-05 - Paper-2 - (Code-B) - (2022-24) - Compile (13-10-2022) - (2020-P-2) - (Only Que.)Document13 pagesUT (A) - CoE (XI) - Test-05 - Paper-2 - (Code-B) - (2022-24) - Compile (13-10-2022) - (2020-P-2) - (Only Que.)darling deanNo ratings yet
- Volume and surface area of prisms homeworkDocument3 pagesVolume and surface area of prisms homeworkroch ajionoNo ratings yet
- Statics, Lecture Notes, Chapter 4Document114 pagesStatics, Lecture Notes, Chapter 4RayanNo ratings yet
- 2-D Cylindrical Roller ContactDocument51 pages2-D Cylindrical Roller ContactDan Wolf100% (1)
- ACI code requirements for structural concrete parametersDocument5 pagesACI code requirements for structural concrete parametersOscarCVNo ratings yet
- Maxima and AtesDocument16 pagesMaxima and AtesJay ZamoraNo ratings yet