Professional Documents
Culture Documents
An Ode Approach To Decision Making Involving Pairwise Comparison of Choices Part 1
Uploaded by
Jomar RabajanteOriginal Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
An Ode Approach To Decision Making Involving Pairwise Comparison of Choices Part 1
Uploaded by
Jomar RabajanteCopyright:
Available Formats
AN ODE APPROACH TO DECISION MAKING INVOLVING PAIRWISE COMPARISON OF CHOICES
YUICHI T. OTSUKA
A Special Problem Presented to the Faculty of the Mathematics Division Institute of Mathematical Sciences and Physics College of Arts and Sciences University of the Philippines Los Baos
In Partial Fulfilment of the Requirements for the Degree of
Bachelor of Science in Applied Mathematics
October 2011
The Faculty of the Mathematics Division Institute of Mathematical Sciences and Physics College of Arts and Sciences University of the Philippines Los Baos Hereby accepts the Special Problem entitled
AN ODE APPROACH TO DECISION MAKING INVOLVING PAIRWISE COMPARISON OF CHOICES
by YUICHI T. OTSUKA
In Partial Fulfilment of the Requirements for the Degree of Bachelor of Science in Applied Mathematics
_____________________________________ MR. JOMAR F. RABAJANTE Special Problem Adviser ___________________ Date _______________________________________ PROF. ARIEL L. BABIERRA Head, Mathematics Division ___________________ Date
_______________________________________ DR. VIRGILIO P. SISON Director, Institute of Mathematical Sciences and Physics ___________________ Date
ii
ABSTRACT
AN ODE APPROACH TO DECISION MAKING INVOLVING PAIRWISE COMPARISON OF CHOICES
Yuichi T. Otsuka UP Los Baos, October 2011
Adviser: Jomar F. Rabajante
In this study, an alternative approach to Analytic Hierarchy Process (AHP) for Multi-Criteria Decision Making (MCDM) was established. With the aid of pairwise comparisons among choices, three models using systems of ordinary differential equations were formulated. The models were used to observe the dynamics of decision making, as well as the qualitative behavior of the interaction that exists among the choices. Numerical and analytic methods were applied to solve the given systems of ordinary differential equations. Though the solutions to the three models differ in nature, the qualitative interpretations were similar. Further analyses were also done on some models, such as finding the period and the absolute extrema for bounded solutions.
iii
ACKNOWLEDGEMENTS
No one else but the Lord witnessed all of what I had gone through in finishing this Special Problem. Nonetheless, I have shared many parts of this journey to a lot of people, to whom I am very much grateful: To my adviser, Sir Jomar Rabajante, for guiding me every step of the way. I have been a hard-to-handle student. Thank you for the patience and understanding. I have bothered you beyond what is necessary. You have taught me far more than what is required of you as an adviser. Youre a blessing sir. To my ODE Professor and brother in Christ, Prof. Vernel Lawas, for the strong background and source of spiritual strength. Little did I know that I have frequented my lecture notes for my exams and for my Special Problem. You are not aware that you have been a father to students like me. Thank you and God bless sir. To all my other educators, you have imbued in me a sense of responsibility through all the years of learning inside and beyond the four walls of the classroom. For my educators this first semester, many times I have not been in my best, thank you for understanding me. To my parents, Kenji and Leticia, I havent gone home frequently due to pressing matters. This is one of them. Your pieces of advice, though not Mathematical in nature, have reached a long way. To my brother, Kenneth, I have usually gone home with a weary heart. We arent in best terms, but I know you have absorbed most of my shortcomings. Thank you. To Ninong Romel and Lolo MJ, for being there. Your presence during the times I have lost the logic and sanity I needed was enough. Nong, I cannot even recall the number of times you have read my drafts and had given me revisions. Lo, thank you for the endless arguments over the phone.
iv
To Ate Aja, Ninang Eloi, Ate Andria, and Maricar, for inspiring me. To my inaanaks Pearl, Jerna, Nowie and Kathleen, my angels. I havent understood girls, and I dont think I ever will. But one things for sure, I learned that no matter how busy you are, you should always have time for them, my Special Problem included. To the Society of Math Majors, one of the families I have, thank you for taking me in. I have been blessed with such a family that made me strong in college. I entered as an innocent child, and came out as a not-so-innocent man anymore, in a good way. I have been and always will be an SMM member. To my co-officers in the organization, and to my SMM batchmates Point of Tangency, thank you for understanding me as I went through this hurdle. Thank you for being there when I wasnt able to perform my duties well as a member and as an officer. I wasnt afraid to fall because I know you were eager to see me rise again. I am in deep gratitude. To Ana Carandang, Merryl Canlas and Robert Capati, for many things that need not be said. Thank you for not pressing me to finish this Special Problem; the reverse psychology worked anyway. All these times you have made me realize that life is hard to handle, time is hard to manage, true friends are hard to find, and that I am such a lucky guy. To Him, for this Special Problem. I believe he doesnt give challenges that we cannot accomplish. Thank you Lord.
Yuichi T. Otsuka
TABLE OF CONTENTS
Abstract . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . iii List of Tables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . viii List of Figures . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ix
1 Introduction 1.1 Objectives . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 1.2 Significance of the Study . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 1.3 Scope and Limitations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 1.4 Time and Place of Study . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 2 Review of Related Literature . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 3 Analytic Hierarchy Process 3.1 Determining the Ranking of Decision Alternatives . . . . . . . . . . . . . . . . . . . . . 9 3.2 Illustrations on AHP . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 4 Model 1 4.1 Model Formulation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18 4.2 Illustration of Model 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20 5 Model 2 5.1 Model Formulation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22 5.2 Illustration of Model 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
vi
6 Model 3 6.1 Model Formulation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26 6.2 Illustration of Model 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32 7 Analytic Solutions for Model 2 7.1 Case 1: One Alternative . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35 7.2 Case 2: Two Alternatives . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36 7.3. Case 3: Three Alternatives . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39 7.4 Periodicity of the Analytic Solutions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42 7.5 Absolute Extrema of the Analytic Solutions . . . . . . . . . . . . . . . . . . . . . . . . . 44 7.6 Relative Extrema of the Analytic Solutions on the Interval 8 More Illustrations 8.1 Rock-Paper-Scissor Interaction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46 8.2 An Extension to the Rock-Paper-Scissor Interaction . . . . . . . . . . . . . . . . . . . 49 8.3 Four Ordered Decision Alternatives . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49 9 Conclusions and Recommendations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52 . . . . . . . . 45
References . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
vii
LIST OF TABLES
TABLE 3.2.1 A Summary of the Relative and Composite Weights in the Illustration
PAGE 16
viii
LIST OF FIGURES
FIGURE 3.1.1 3.1.2 3.2.1 4.2.1 Flow of AHP Calculations with 1 Decision Criterion Flow of AHP Computations with Decision Criteria
PAGE 11 11 13 21
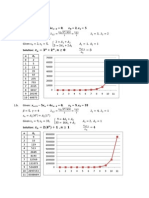
Flow of Calculations for the Illustration Numerical Solution for Model 1 Illustration Using Berkeley Madonna
5.2.1
Numerical Solution for Model 2 Illustration Using Berkeley Madonna
25
6.1.1 6.1.2
Network Diagram: Directed Complete Graph with Network Diagram: Directed Complete Graph with Weights
Nodes Nodes, with
27 27
6.1.3 6.1.4 6.1.5 6.1.6 6.1.7 6.2.1
Network Diagram with Primary Reference Node Network Diagram with Secondary Reference Node Network Diagram with Secondary Reference Node Network Diagram with Secondary Reference Node Network Diagram with Secondary Reference Node Numerical Solution for Model 3 Illustration Using Berkeley Madonna
28 29 30 30 30 33
8.1.1 8.1.2 8.1.3
Numerical Solution to Rock-Paper-Scissor Interaction, Model 1 Numerical Solution to Rock-Paper-Scissor Interaction, Model 2 Numerical Solution to Rock-Paper-Scissor Interaction, Model 3
48 48 48
ix
8.3.1 8.3.2 8.3.3
Numerical Solution with Four Decision Alternatives, Model 1 Numerical Solution with Four Decision Alternatives, Model 2 Numerical Solution with Four Decision Alternatives, Model 3
51 51 51
You might also like
- Introduction To Probability For Data ScienceDocument70 pagesIntroduction To Probability For Data Sciencelacoste--lacosteNo ratings yet
- Random Differential Equations in Science and EngineeringFrom EverandRandom Differential Equations in Science and EngineeringNo ratings yet
- A First Course in Experimental DesignDocument193 pagesA First Course in Experimental DesignHaneen WaleedNo ratings yet
- George Parker Lamptey PDFDocument101 pagesGeorge Parker Lamptey PDFcentkiloNo ratings yet
- Making Math Learning Fun for Inner City School StudentsFrom EverandMaking Math Learning Fun for Inner City School StudentsGlendolyn Duhon-JeanlouisNo ratings yet
- bfm:978 0 387 74995 2/1 PDFDocument13 pagesbfm:978 0 387 74995 2/1 PDFAbdoulaye NiangNo ratings yet
- Theory of Preliminary Test and Stein-Type Estimation with ApplicationsFrom EverandTheory of Preliminary Test and Stein-Type Estimation with ApplicationsNo ratings yet
- Texts in Applied Mathematics Editors-In-Chief Introduction To Uncertainty QuantificationDocument351 pagesTexts in Applied Mathematics Editors-In-Chief Introduction To Uncertainty QuantificationŞıhmehmet YıldızNo ratings yet
- Introduction To Uncertainty QuantificationDocument351 pagesIntroduction To Uncertainty QuantificationSadiq Sarfaraz100% (3)
- Chihara Et Al-Mathematical Statistics With Re Sampling and R-2011-ToC - 201Document8 pagesChihara Et Al-Mathematical Statistics With Re Sampling and R-2011-ToC - 201uri20No ratings yet
- BookDocument443 pagesBookShakeel Ahmad KasuriNo ratings yet
- Statistical Tolerance Regions: Theory, Applications, and ComputationFrom EverandStatistical Tolerance Regions: Theory, Applications, and ComputationNo ratings yet
- Asquith DissertationDocument461 pagesAsquith Dissertation115319No ratings yet
- Peterson's MCAT SuccessDocument840 pagesPeterson's MCAT SuccessMing WanNo ratings yet
- Course PackDocument129 pagesCourse Packham.karimNo ratings yet
- PDFDocument291 pagesPDFNA Med100% (3)
- The Ring Theory and The Representation Theory of Quantum SchubertDocument109 pagesThe Ring Theory and The Representation Theory of Quantum SchubertCherry GalvezNo ratings yet
- Abstract Algebra For Beginners - BeachyDocument177 pagesAbstract Algebra For Beginners - Beachycantor2000100% (1)
- Learning From Data - A Short CourseDocument215 pagesLearning From Data - A Short Coursem_sifalakis91% (11)
- Lebl - Basic AnalysisDocument252 pagesLebl - Basic AnalysispastafarianboyNo ratings yet
- V Foreword VI Preface VII Authors' Profiles VIII Convention Ix Abbreviations X List of Tables Xi List of Figures Xii 1 1Document152 pagesV Foreword VI Preface VII Authors' Profiles VIII Convention Ix Abbreviations X List of Tables Xi List of Figures Xii 1 1July Rodriguez100% (3)
- Econometric SDocument348 pagesEconometric Sbizjim20067960No ratings yet
- Bielajew, A. F. - Introduction To Computers and Programming Using C++ and MATLAB - 2002Document440 pagesBielajew, A. F. - Introduction To Computers and Programming Using C++ and MATLAB - 2002Natrix2No ratings yet
- Differential Equations A Linear Algebra Approach (Anindya Dey)Document626 pagesDifferential Equations A Linear Algebra Approach (Anindya Dey)Meliza Souza100% (2)
- Applied Bayesian Modeling and Causal Inference from Incomplete-Data PerspectivesFrom EverandApplied Bayesian Modeling and Causal Inference from Incomplete-Data PerspectivesNo ratings yet
- C&Matlab PrimerDocument412 pagesC&Matlab Primerapi-3734979No ratings yet
- SCIE1000 Theory and Practice in Science NotesDocument442 pagesSCIE1000 Theory and Practice in Science NotesTerry GaoNo ratings yet
- Introduction To Computers and ProgrammingDocument441 pagesIntroduction To Computers and ProgrammingShan ShahNo ratings yet
- Abstract Mathematics Mt2116 Ch1-3Document50 pagesAbstract Mathematics Mt2116 Ch1-3diamond3187No ratings yet
- Anoka - Hennepin - Probability - and - Statistics-4 2013 NEW - 4 PDFDocument357 pagesAnoka - Hennepin - Probability - and - Statistics-4 2013 NEW - 4 PDFSoniyaKanwalG100% (2)
- Doan Uccs 0892D 10279Document147 pagesDoan Uccs 0892D 10279asma khanNo ratings yet
- Berth and Quay Crane Scheduling: Problems, Models and Solution MethodsDocument185 pagesBerth and Quay Crane Scheduling: Problems, Models and Solution MethodsMrManagerNo ratings yet
- Parameter Estimation and Inverse ProblemsDocument9 pagesParameter Estimation and Inverse Problemsdebora sNo ratings yet
- Nano Mechanics and Materials: Theory, Multiscale Methods and ApplicationsFrom EverandNano Mechanics and Materials: Theory, Multiscale Methods and ApplicationsNo ratings yet
- Boltzmann Transformation Approach To Simulate A Two Phase Radial Diffusivity Model For Tight Oil ReservoirsDocument86 pagesBoltzmann Transformation Approach To Simulate A Two Phase Radial Diffusivity Model For Tight Oil ReservoirsheliaNo ratings yet
- Math Phonics Fractions: Quick Tips and Alternative Techniques for Math MasteryFrom EverandMath Phonics Fractions: Quick Tips and Alternative Techniques for Math MasteryNo ratings yet
- ResearchDocument160 pagesResearchclifford henryNo ratings yet
- Testes de Qualidade de AjusteDocument113 pagesTestes de Qualidade de AjustePedro Humberto Almeida GonzagaNo ratings yet
- Prob & StatDocument226 pagesProb & StatdeepakaniNo ratings yet
- mt1173 Vle PDFDocument287 pagesmt1173 Vle PDFKhushal JhajahriaNo ratings yet
- Yaser S. Abu-Mostafa, Malik Magdon-Ismail, Hsuan-Tien Lin-Learning From Data - A Short course-AMLBook - Com (2012) PDFDocument215 pagesYaser S. Abu-Mostafa, Malik Magdon-Ismail, Hsuan-Tien Lin-Learning From Data - A Short course-AMLBook - Com (2012) PDFPrateek Agrawal86% (7)
- Collaborative Statistics Teacher's GuideDocument59 pagesCollaborative Statistics Teacher's GuidejojojNo ratings yet
- LSE Abstract MathematicsDocument251 pagesLSE Abstract Mathematicsgattling100% (1)
- bfm-978-3-540-70989-3-1 BookDocument8 pagesbfm-978-3-540-70989-3-1 BookTavamani MuniandyNo ratings yet
- Engineering MathematicsDocument313 pagesEngineering Mathematicsk4p98zshvhNo ratings yet
- For The Love of ACT ScienceDocument125 pagesFor The Love of ACT ScienceTung Hoang100% (7)
- Notes BiomathDocument283 pagesNotes BiomathAndrea Espinosa67% (3)
- Lecture Notes in Mathematical Biology-E.D.sontagDocument126 pagesLecture Notes in Mathematical Biology-E.D.sontagAarón Castillo JiménezNo ratings yet
- Algorithmic Mathematics (Hougardy, Stefan, Vygen, Jens)Document167 pagesAlgorithmic Mathematics (Hougardy, Stefan, Vygen, Jens)onesimus75% (4)
- Academic Writing for Military Personnel, revised edition: Revised EditionFrom EverandAcademic Writing for Military Personnel, revised edition: Revised EditionNo ratings yet
- An Ode Approach To Decision Making Involving Pairwise Comparison of Choices Part 3Document55 pagesAn Ode Approach To Decision Making Involving Pairwise Comparison of Choices Part 3Jomar RabajanteNo ratings yet
- Escaneritem Item 2, 3 and 6Document4 pagesEscaneritem Item 2, 3 and 6Jomar RabajanteNo ratings yet
- JFRabajante MS Applied Math ThesisDocument179 pagesJFRabajante MS Applied Math ThesisJomar Rabajante100% (2)
- UPLB Biomath GroupDocument13 pagesUPLB Biomath GroupJomar RabajanteNo ratings yet
- Item 3 Part 2Document1 pageItem 3 Part 2Jomar RabajanteNo ratings yet
- Optimal Migration Strategy of Species Foraging On Patchily Distributed Food SourcesDocument27 pagesOptimal Migration Strategy of Species Foraging On Patchily Distributed Food SourcesJomar RabajanteNo ratings yet
- Digitized SignaturesDocument11 pagesDigitized SignaturesJomar RabajanteNo ratings yet
- An Ode Approach To Decision Making Involving Pairwise Comparison of Choices Part 2Document1 pageAn Ode Approach To Decision Making Involving Pairwise Comparison of Choices Part 2Jomar RabajanteNo ratings yet
- Beamer TemplateDocument51 pagesBeamer TemplateJomar RabajanteNo ratings yet
- Directions Going To UPLBDocument3 pagesDirections Going To UPLBJomar RabajanteNo ratings yet
- Item 3 Part 1Document2 pagesItem 3 Part 1Jomar RabajanteNo ratings yet
- Zarraga P-Noy-mial InterpolationDocument1 pageZarraga P-Noy-mial InterpolationJomar RabajanteNo ratings yet
- A World of Bizarre Things: AppliedDocument38 pagesA World of Bizarre Things: AppliedJomar RabajanteNo ratings yet
- Accommodations in and Near UPLBDocument23 pagesAccommodations in and Near UPLBJomar Rabajante70% (10)
- A Denial of The Universality of LogicDocument1 pageA Denial of The Universality of LogicJomar RabajanteNo ratings yet
- Escaner Item 1, 4 and 5Document2 pagesEscaner Item 1, 4 and 5Jomar RabajanteNo ratings yet
- Jomar Fajardo Rabajante MATH 235 2002-96301 Problem SetDocument8 pagesJomar Fajardo Rabajante MATH 235 2002-96301 Problem SetJomar RabajanteNo ratings yet
- Item 4Document2 pagesItem 4Jomar RabajanteNo ratings yet
- Item 5Document2 pagesItem 5Jomar RabajanteNo ratings yet
- Poly SyDocument7 pagesPoly SyJomar RabajanteNo ratings yet
- DX DT V V DX DT V V DX DT V V V X, X Constants: Jomar Fajardo Rabajante MATH 235 2002-96301 Problem SetDocument4 pagesDX DT V V DX DT V V DX DT V V V X, X Constants: Jomar Fajardo Rabajante MATH 235 2002-96301 Problem SetJomar RabajanteNo ratings yet
- Determining The Optimal Distribution of Bee Colony Locations To Avoid Overpopulation Using Mixed Integer ProgrammingDocument9 pagesDetermining The Optimal Distribution of Bee Colony Locations To Avoid Overpopulation Using Mixed Integer ProgrammingJomar RabajanteNo ratings yet
- Biomath FinalDocument25 pagesBiomath FinalJomar RabajanteNo ratings yet
- Fractals in The 2006 Philippines Family Annual Income Distribution DataDocument1 pageFractals in The 2006 Philippines Family Annual Income Distribution DataJomar RabajanteNo ratings yet
- When The Customer Writes His Own Story ManilaDocument9 pagesWhen The Customer Writes His Own Story ManilaJomar RabajanteNo ratings yet
- Determining The Optimal Distribution of Bee Colony LocationsDocument30 pagesDetermining The Optimal Distribution of Bee Colony LocationsJomar RabajanteNo ratings yet
- The Passing Rate SimulatorDocument13 pagesThe Passing Rate SimulatorJomar RabajanteNo ratings yet
- Area Restrict BiroiDocument23 pagesArea Restrict BiroiJomar RabajanteNo ratings yet
- Assignment # 4 MomentsDocument9 pagesAssignment # 4 MomentsKalidNo ratings yet
- Civil Engineering: Reinforced Cement Concrete & Pre-Stressed ConcreteDocument33 pagesCivil Engineering: Reinforced Cement Concrete & Pre-Stressed ConcreteDebendra Dev KhanalNo ratings yet
- Answer KeyDocument22 pagesAnswer Keyjohnbenedictviernes308No ratings yet
- Maximum Moisture Content MethodDocument9 pagesMaximum Moisture Content MethodGuilherme PrataNo ratings yet
- Physics Duty Chapter SevenDocument23 pagesPhysics Duty Chapter SevenScribdTranslationsNo ratings yet
- Metals 10 01121Document14 pagesMetals 10 01121dietersimaNo ratings yet
- Arc VoltageDocument3 pagesArc Voltagedbharanidharan_in6351No ratings yet
- SM04 Poster 82Document6 pagesSM04 Poster 82lkamalNo ratings yet
- E 881511 Om GSCTP C P RC GBR 6-A4Document72 pagesE 881511 Om GSCTP C P RC GBR 6-A4winarnobNo ratings yet
- Application of The Giroud - Han Design Method For Geosynthetic Reinforced Unpaved Roads With Tencate Mirafi GeosyntheticsDocument7 pagesApplication of The Giroud - Han Design Method For Geosynthetic Reinforced Unpaved Roads With Tencate Mirafi GeosyntheticsFaten Abou ShakraNo ratings yet
- CTV PRC001 E4 - 09012004 PDFDocument24 pagesCTV PRC001 E4 - 09012004 PDFsuperpuma86No ratings yet
- Genetic Algorithms in OptimizationDocument38 pagesGenetic Algorithms in OptimizationssbhonsaleNo ratings yet
- Ed081p36 1Document1 pageEd081p36 1IHN SisNo ratings yet
- Lesson 1.3: General Properties of Indefinite IntegralsDocument6 pagesLesson 1.3: General Properties of Indefinite IntegralsMarkNo ratings yet
- Chapter Thirteen Solutions Chapter Thirteen SolutionsDocument13 pagesChapter Thirteen Solutions Chapter Thirteen Solutionsdavid bustilloNo ratings yet
- Fishers LDADocument47 pagesFishers LDABinduNo ratings yet
- 7th Semester UET TaxilaDocument4 pages7th Semester UET TaxilaRameez AnwarNo ratings yet
- Numerical Solutions of The Integral Equations of The First KindDocument8 pagesNumerical Solutions of The Integral Equations of The First KindRashed2010100% (1)
- Lecture 3Document10 pagesLecture 3Abhishek SinhaNo ratings yet
- PETREL 1 Structural Modeling PDFDocument42 pagesPETREL 1 Structural Modeling PDFKuala Tambora100% (1)
- Mechanical EngineeringDocument19 pagesMechanical EngineeringhenoksolNo ratings yet
- USP 905 - Uniformity of Dosage UnitsDocument4 pagesUSP 905 - Uniformity of Dosage UnitsLisa DebrowskiNo ratings yet
- Design and testing of an oil-based pressure-compensated underwater hydraulic systemDocument12 pagesDesign and testing of an oil-based pressure-compensated underwater hydraulic systemGanesh ChodisettiNo ratings yet
- GPS100 Data SheetDocument2 pagesGPS100 Data SheetCaptainNo ratings yet
- Diffusion Equations: Separation of Variables and EigenvaluesDocument22 pagesDiffusion Equations: Separation of Variables and EigenvaluesTaterRayGumfriesNo ratings yet
- PGZ Schwenken EnglDocument36 pagesPGZ Schwenken EngljonNo ratings yet
- Structures: Muhammad Zain, Muhammad Usman, Syed Hassan FarooqDocument11 pagesStructures: Muhammad Zain, Muhammad Usman, Syed Hassan FarooqDilum VRNo ratings yet
- Osmosis and Diffusion Lab VocabularyDocument3 pagesOsmosis and Diffusion Lab Vocabularydannyf09No ratings yet
- CFD Application Tutorials 2Document35 pagesCFD Application Tutorials 2Jubril AkinwandeNo ratings yet