Professional Documents
Culture Documents
Greedy Programming
Uploaded by
akg299Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Greedy Programming
Uploaded by
akg299Copyright:
Available Formats
Greedy Programming
Deliverables
Greedy Paradigm
Coin Change Problem
Interval Scheduling
Optimal Merge Sort
Huffman compression
0/1 and partial knapsack
Minimizing Lateness
6/7/2012 8:57 PM Copyright @ gdeepak.Com 2
Greedy paradigm
Primarily used in Optimization problems to find
the maximum or minimum value satisfying
given constraints.
It helps in constructing solution for a problem by
a sequence of steps (piecewise) where each step
is considered a partial solution, which is
extended progressively to get complete solution.
6/7/2012 8:57 PM Copyright @ gdeepak.Com 3
Choice of steps
Choice of each step in greedy is based on following
It must be feasible
It must be locally optimal
It must be irrevocable
Locally optimal choice is considered globally optimal.
6/7/2012 8:57 PM Copyright @ gdeepak.Com 4
5 Pillars of Greedy Technique
Proof of correctness is necessary and important.
1. A candidate set, from which a solution is created
2. A selection function, which chooses the best candidate to be
added to the solution
3. A feasibility function that is used to determine if a candidate
can be used to contribute to a solution
4. An objective function, which assigns a value to a solution, or
a partial solution, and
5. A solution function, which will indicate when we have
discovered a complete solution
6/7/2012 8:57 PM Copyright @ gdeepak.Com 5
General Greedy Algorithm
a[1:n]; sol ;
for i 1 to n do
x SELECT(a); //as per some optimization criteria
if FEASIBLE(sol, x) then solution UNION(sol, x);
return sol
Feasibility checks whether the selected element meets the
feasibility criteria and Union integrates the element x in the
solution
6/7/2012 8:57 PM Copyright @ gdeepak.Com 6
Coin Change Problem
An amount and collection of coins to reach to that amount Objective is to
minimize the number of coins
Greedy theory says always return the largest coin
if coins are of denomination 32, 8, 1 it has the greedy choice property because
no amount over 32 can be made without omitting 32.
if coins are of denomination 30,20,5,1 then it doesnt have greedy choice
property because 40 can be made with two 20 coins but it returns 30,5,5 coins
Similarly if denominations are 1, 10, 21, 34, 70, 100, 350 140 Greedy: 100, 34,
1, 1, 1, 1, 1, 1 Optimal: 70, 70
6/7/2012 8:57 PM Copyright @ gdeepak.Com 7
Interval Scheduling Problem
Given set S = {a1, , an} of activities and activity start and
finish times, e.g.
i 1 2 3 4 5 6 7 8 9 10 11
si 1 3 0 5 3 5 6 8 8 2 12
fi 4 5 6 7 8 9 10 11 12 13 14
Activities are compatible if their time intervals do not
overlap, i.e., ai is compatible with aj is si fj or sj fi.
To find Subset of non overlapping intervals so that number
of intervals are maximum.
6/7/2012 8:57 PM Copyright @ gdeepak.Com 8
Earliest Start Time
6/7/2012 8:57 PM Copyright @ gdeepak.Com 9
Shortest interval First
6/7/2012 8:57 PM Copyright @ gdeepak.Com 10
Fewest Conflicts First
6/7/2012 8:57 PM Copyright @ gdeepak.Com 11
Interval Scheduling Algorithm
Interval that ends first and remove the intervals that
overlap with these and recurse.
Sort jobs by finish times so that f1 f2 ... fn.
A
for j = 1 to n
{
if (job j compatible with A)
A A {j}
}
return A
6/7/2012 8:57 PM Copyright @ gdeepak.Com 12
Efficient greedy algorithm
Once youve identified a reasonable greedy heuristic:
Prove that it always gives the correct answer
Develop an efficient solution
6/7/2012 8:57 PM Copyright @ gdeepak.Com 13
Is our greedy approach correct?
Stays ahead argument: show that no matter what other
solution someone provides you, the solution provided by
your algorithm always stays ahead, in that no other
choice could do better
6/7/2012 8:57 PM Copyright @ gdeepak.Com 14
Is our greedy approach correct?
Stays ahead argument
Let r1, r2, r3, , rk be the solution found by our approach
r1 r2 r3
rk
Let o1, o2, o3, , ok of another optimal solution
o1 o2 o3
ok
Show our approach stays ahead of any other solution
6/7/2012 8:57 PM Copyright @ gdeepak.Com 15
Stays ahead
r1 r2 r3
rk
o1 o2 o3
ok
Compare first activities of each solution
6/7/2012 8:57 PM Copyright @ gdeepak.Com 16
Stays ahead
r1 r2 r3
rk
o1 o2 o3
ok
finish(r1) finish(o1)
6/7/2012 8:57 PM Copyright @ gdeepak.Com 17
Stays ahead
r2 r3
rk
o2 o3
ok
We have at least as much time as any other solution to schedule
remaining 2k tasks
6/7/2012 8:57 PM Copyright @ gdeepak.Com 18
Optimal Merge Sort
Suppose there are 3 sorted lists L1, L2, and L3, of sizes 30, 20, and 10,
respectively, which need to be merged into a combined sorted list but
we can merge only two at a time.
We intend to find an optimal merge pattern which minimizes the total
number of comparisons.
Merge L1 & L2,: 30 + 20 = 50 comparisons , then merge the list & L3:
50 + 10 = 60 comparisons total number of comparisons: 50 + 60 = 110.
Alternatively, merge L2 & L3: 20 + 10 = 30 comparisons, the resulting
list (size 30) then merge the list with L1: 30 + 30 = 60 total number of
comparisons: 30 + 60 = 90.
6/7/2012 8:57 PM Copyright @ gdeepak.Com 19
Merge sort example
6/7/2012 8:57 PM Copyright @ gdeepak.Com 20
Huffman Compression
File f has one million characters. If only a, b, c, d, e, f chars come in the file then the
total size of the file is 8 million bits
If we represent these with 000 001 010 011 101 111 then only 3 million bits
0 1 00 11 10 11 will give us less then 2 million bits
Assume frequency of occurrence of a, b, c, d, e, f is 45%,13%,12%,16%,9%,5%
leaves of the binary tree will represent the bit strings
It will give us the prefix free code. use greedy for making the binary tree and then
assign 0 to every left node and 1 to every right node. The nodes with larger frequency
will be nearer to the root and with lesser frequency will be towards the leaves.
6/7/2012 8:57 PM Copyright @ gdeepak.Com 21
Huffman Example
6/7/2012 8:57 PM Copyright @ gdeepak.Com 22
Knapsack
Given n objects and a knapsack. Object i has weight wi and the
knapsack has a capacity M.
if a fraction xi, 0<= xi <= 1 of object i is placed into the knapsack
then a profit of pixi is earned. The objective is to obtain a filling of
the knapsack that maximizes the total profit earned.
Since knapsack capacity is M, total weight of all chosen objects
should be M. The profits and weights are positive
6/7/2012 8:57 PM Copyright @ gdeepak.Com 23
Partial Knapsack-Greedy
6/7/2012 8:57 PM Copyright @ gdeepak.Com 24
0/1 knapsack
1st is optimal but greedy will give 2nd solution
6/7/2012 8:57 PM Copyright @ gdeepak.Com 25
Algorithm for partial knapsack
Input Set S of items with weight wi , benefit bi and total weight W
Output amount xi of each item i to maximize benefit with weight
W for each item i in S
xi=0
vi=bi/wi
w=0
while w<W
remove item i with highest vi
xi=min(wi, W-w)
w=w+min(wi, W-w)
6/7/2012 8:57 PM Copyright @ gdeepak.Com 26
Job deadlines
Single resource processes one job at a time.
Job j requires tj units of processing time and is due at time dj.
If j starts at time sj, it finishes at time fj = sj + tj.
Lateness: lj = max { 0, fj - dj }.
Goal: Schedule all jobs to minimize maximum lateness
L=max lj.
1 2 3 4 5 6
tj 3 2 1 4 3 2
dj 6 8 9 9 14 15
6/7/2012 8:57 PM Copyright @ gdeepak.Com 27
Minimizing lateness
Consider jobs in ascending order of processing time tj
1 2
tj 1 10
dj 100 10
Consider jobs in ascending order of slack dj - tj
1 2
tj 1 10
dj 2 10
6/7/2012 8:57 PM Copyright @ gdeepak.Com 28
Minimizing Lateness
Consider Jobs in the sequence of earliest deadline first
T 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
J 1 1 1 2 2 3 4 4 4 4 5 5 5 6 6
D 6 6 6 8 8 9 9 9 9 9L 14 14 14 15 15
6/7/2012 8:57 PM Copyright @ gdeepak.Com 29
Single Job-Single resource
There is no preemption and these have to be allocated
processor. Only one processor is available. Objective is to
minimize the sum of the finishing times
f1=t1
f2=t1+t2
fi=t1+t2++ti
:
fn=nt1+(n-1)t2++tn
So t1 should be smallest and so on
6/7/2012 8:57 PM Copyright @ gdeepak.Com 30
Questions, Suggestions and Comments
6/7/2012 8:57 PM Copyright @ gdeepak.Com 31
Question 1
Considering the following graph as a multi stage graph and using
Greedy Approach the shortest path is
A) 9
B) 23
C) 5
D) 17
6/7/2012 8:57 PM Copyright @ gdeepak.Com 32
Question 2
Greedy Technique is related to the theory of
A) Calculus
B) Probability
C) Matroid
D) Algebra
6/7/2012 8:57 PM Copyright @ gdeepak.Com 33
Question 3
For those problems where Greedy gives the optimal
solution, the complexity is better as compared to the
implementation of the same problem with Dynamic
Programming.
A) True
B) False
6/7/2012 8:57 PM Copyright @ gdeepak.Com 34
??
Given a question, Can you find whether greedy strategy
work in general is NP-Complete.
6/7/2012 8:57 PM Copyright @ gdeepak.Com 35
You might also like
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeFrom EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeRating: 4 out of 5 stars4/5 (5794)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreFrom EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreRating: 4 out of 5 stars4/5 (1090)
- Never Split the Difference: Negotiating As If Your Life Depended On ItFrom EverandNever Split the Difference: Negotiating As If Your Life Depended On ItRating: 4.5 out of 5 stars4.5/5 (838)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceFrom EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceRating: 4 out of 5 stars4/5 (895)
- Grit: The Power of Passion and PerseveranceFrom EverandGrit: The Power of Passion and PerseveranceRating: 4 out of 5 stars4/5 (588)
- Shoe Dog: A Memoir by the Creator of NikeFrom EverandShoe Dog: A Memoir by the Creator of NikeRating: 4.5 out of 5 stars4.5/5 (537)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersFrom EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersRating: 4.5 out of 5 stars4.5/5 (345)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureFrom EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureRating: 4.5 out of 5 stars4.5/5 (474)
- Her Body and Other Parties: StoriesFrom EverandHer Body and Other Parties: StoriesRating: 4 out of 5 stars4/5 (821)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)From EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Rating: 4.5 out of 5 stars4.5/5 (121)
- The Emperor of All Maladies: A Biography of CancerFrom EverandThe Emperor of All Maladies: A Biography of CancerRating: 4.5 out of 5 stars4.5/5 (271)
- The Little Book of Hygge: Danish Secrets to Happy LivingFrom EverandThe Little Book of Hygge: Danish Secrets to Happy LivingRating: 3.5 out of 5 stars3.5/5 (400)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyFrom EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyRating: 3.5 out of 5 stars3.5/5 (2259)
- The Yellow House: A Memoir (2019 National Book Award Winner)From EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Rating: 4 out of 5 stars4/5 (98)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaFrom EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaRating: 4.5 out of 5 stars4.5/5 (266)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryFrom EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryRating: 3.5 out of 5 stars3.5/5 (231)
- Team of Rivals: The Political Genius of Abraham LincolnFrom EverandTeam of Rivals: The Political Genius of Abraham LincolnRating: 4.5 out of 5 stars4.5/5 (234)
- On Fire: The (Burning) Case for a Green New DealFrom EverandOn Fire: The (Burning) Case for a Green New DealRating: 4 out of 5 stars4/5 (74)
- The Unwinding: An Inner History of the New AmericaFrom EverandThe Unwinding: An Inner History of the New AmericaRating: 4 out of 5 stars4/5 (45)
- Image Caption Technical ReportDocument28 pagesImage Caption Technical Reportakg29950% (2)
- Operations Research - 2013Document106 pagesOperations Research - 2013vinit557% (7)
- Product Teardown: By: Eesha VermaDocument20 pagesProduct Teardown: By: Eesha Vermaakg299No ratings yet
- Bossy PantsDocument1 pageBossy Pantsakg2990% (1)
- Product Teardown: Made By: Eesha VermaDocument19 pagesProduct Teardown: Made By: Eesha Vermaakg299No ratings yet
- Book Review Designing Data-Intensive Applications: The Big Ideas Behind ReliableDocument4 pagesBook Review Designing Data-Intensive Applications: The Big Ideas Behind Reliableakg299No ratings yet
- Ucs742 AssignmentDocument1 pageUcs742 Assignmentakg299No ratings yet
- Multichannel Variable-Size Convolution For Sentence ClassificationDocument13 pagesMultichannel Variable-Size Convolution For Sentence Classificationakg299No ratings yet
- Image Captioning TRDocument5 pagesImage Captioning TRakg299No ratings yet
- Technical Report: Image Captioning With Semantically Similar ImagesDocument3 pagesTechnical Report: Image Captioning With Semantically Similar Imagesakg299No ratings yet
- GFG Array Questions ImportantDocument6 pagesGFG Array Questions Importantakg299No ratings yet
- ZS Campus Name 2018 Student DataDocument2 pagesZS Campus Name 2018 Student Dataakg299No ratings yet
- Tu6 PDFDocument34 pagesTu6 PDFakg299No ratings yet
- Business Operations Associate PDFDocument2 pagesBusiness Operations Associate PDFakg299No ratings yet
- PNP ProblemsDocument11 pagesPNP Problemsakg299No ratings yet
- Linked ListDocument7 pagesLinked Listakg299No ratings yet
- TAES-2023-0939.R1 Proof HiDocument99 pagesTAES-2023-0939.R1 Proof HiZhongyuan ChenNo ratings yet
- Ie Unit 2Document14 pagesIe Unit 2Devesh DhumalNo ratings yet
- Indian Institute of Technology, Bombay Chemical Engineering Cl603, Optimization Endsem, 27 April 2018Document3 pagesIndian Institute of Technology, Bombay Chemical Engineering Cl603, Optimization Endsem, 27 April 2018Lakshay ChhajerNo ratings yet
- Efficient Plant Layout Design of A Small Scale Textile Industry-A Case StudyDocument3 pagesEfficient Plant Layout Design of A Small Scale Textile Industry-A Case StudyTibebu TameneNo ratings yet
- ME F344 HandoutDocument3 pagesME F344 Handoutrushil guptaNo ratings yet
- User Association in 5G Networks A Survey PDFDocument27 pagesUser Association in 5G Networks A Survey PDFWaleed AlmarshediNo ratings yet
- Saep 349 PDFDocument41 pagesSaep 349 PDFRami ElloumiNo ratings yet
- Linear Programming-Wolfram Mathematica 9 ..Document15 pagesLinear Programming-Wolfram Mathematica 9 ..zhushazangNo ratings yet
- Master Thesis Electrical Power Engineering PDFDocument5 pagesMaster Thesis Electrical Power Engineering PDFtishanoelfrisco100% (1)
- Lesson Plan + Blue PrintDocument6 pagesLesson Plan + Blue PrintDini P. RahmadaniNo ratings yet
- E. LPV System and Gain SchedulingDocument33 pagesE. LPV System and Gain SchedulingJose Ivan CuetoNo ratings yet
- CV George PapazafeiropoulosDocument13 pagesCV George PapazafeiropoulosGeorge PapazafeiropoulosNo ratings yet
- Facility Location Decisions: Alexander Hamilton, 1791Document40 pagesFacility Location Decisions: Alexander Hamilton, 1791TitiNo ratings yet
- A Practical System For Hydrodynamic Optimization of Ship Hull FormsDocument7 pagesA Practical System For Hydrodynamic Optimization of Ship Hull FormsSalma SherbazNo ratings yet
- 2010 Solving Assembly Line Balancing ModelsDocument6 pages2010 Solving Assembly Line Balancing ModelsFrancesc HDNo ratings yet
- Understanding Machine Learning Theory AlgorithmsDocument449 pagesUnderstanding Machine Learning Theory AlgorithmsHigor EduardoNo ratings yet
- TP 03: Technique D'optimisation PSODocument3 pagesTP 03: Technique D'optimisation PSOCEM Yelle N centreNo ratings yet
- Part A: Texas A&M University MEEN 683 Multidisciplinary System Design Optimization (MSADO) Spring 2021 Assignment 2Document5 pagesPart A: Texas A&M University MEEN 683 Multidisciplinary System Design Optimization (MSADO) Spring 2021 Assignment 2BobaNo ratings yet
- Workflow Management SystemDocument16 pagesWorkflow Management SystemBharath GrNo ratings yet
- Paper # 068 - Sag & Ball Mill Control by Model Predictive Controllers On 3 Lines at CollahuasiDocument23 pagesPaper # 068 - Sag & Ball Mill Control by Model Predictive Controllers On 3 Lines at CollahuasicarloscjunoNo ratings yet
- Genetic Algorithm Tools For Control Systems Engineering: Enesys EnitorDocument6 pagesGenetic Algorithm Tools For Control Systems Engineering: Enesys EnitorRamazan SelçukNo ratings yet
- The Assignment Problem: Basic ConceptsDocument51 pagesThe Assignment Problem: Basic Conceptsshouvik palNo ratings yet
- Optimal Placement of Electric Vehicle Charging Station For Unbalanced Radial Distribution SystemsDocument17 pagesOptimal Placement of Electric Vehicle Charging Station For Unbalanced Radial Distribution SystemsArdhito PrimatamaNo ratings yet
- Statistics 580 Maximum Likelihood Estimation: 1 2 N 0 N 1 P 0 PDocument25 pagesStatistics 580 Maximum Likelihood Estimation: 1 2 N 0 N 1 P 0 PTawsif HasanNo ratings yet
- Ethanol Amine ProductionDocument8 pagesEthanol Amine ProductionFatih FıratNo ratings yet
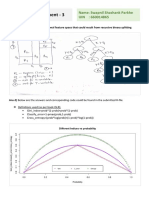
- IDS 575 Assignment - 3: Name: Swapnil Shashank Parkhe UIN: 660014865Document7 pagesIDS 575 Assignment - 3: Name: Swapnil Shashank Parkhe UIN: 660014865Swapnil ParkheNo ratings yet
- Simpro - Task 2-1 - : Guide Rail Optimization by IsightDocument24 pagesSimpro - Task 2-1 - : Guide Rail Optimization by Isightkikokiko KarimNo ratings yet
- ADMAT-Automatic Differentiation Toolbox For Use With MATLABDocument103 pagesADMAT-Automatic Differentiation Toolbox For Use With MATLABalawi747594No ratings yet