UNIT 4 AC CIRCUITS

AC Circuits

Structure
4.1

Introduction
Objectives

4.2

Introduction to Alternating Quantity

4.3

RMS and Average Value

4.3.1

RMS Value of Complex Wave

4.3.2

Average Value

4.3.3

RMS Value of Sinusoidal Wave

4.3.4

Average Value of Sinusoidal

4.3.5

Form Factor

4.3.6

Peak, Crest or Amplitude Factor

4.4

Complex Representation of Alternating Quantities

4.5

Resistive, Inductive and Capacitive Circuits

4.6

4.5.1

Series RLC Circuit

4.5.2

Parallel RLC Circuit

Concept of Power
4.6.1

Power in AC Circuit

4.6.2

Power Triangle

4.7

Power Factor

4.8

Quality Factor (Q-Factor)

4.9

Series and Parallel Resonance

4.9.1

Series Resonance

4.9.2

Parallel Resonance

4.10 Three Phase Circuit

4.10.1 Connections in Three Phase System
4.10.2 Voltage, Current and Power Relation
4.10.3 Conversion from Star Connection to Delta Connection

4.11 Maximum Power Transfer Theorem

4.12 Summary
4.13 Answers to SAQs

4.1 INTRODUCTION
This unit deals with the concept of AC circuit analysis. Unit starts with the basic
definitions about the alternating quantity and then covers the concept of RMS and
average value, form factor and peak factor.
At the latter stage of unit, we give the idea of resistance, inductive and capacitive circuits,
calculation for their voltage, current, power and power factor. We also introduce three
types of powers active, reactive and apparent power. Detail discussions about the series
and parallel RLC circuits is also given in this unit.
The unit also covers the concept of series and parallel resonance with sufficient
description and examples.
Analysis of balanced three phase circuit, star-delta conversion and maximum power
transfer theorem are also the part of this unit.
81

Electrical

Objectives
After studying this unit, you should be able to

explain the concept of alternating quantity,

define the RMS and average values with form and peak factor,

determine the voltage, current and power for pure resistive, inductive,
capacitive circuits and circuit having their combinations,

define the power factor and quality factor,

distinguish between apparent, active and reactive powers,

explain the concept of series and parallel resonance,

distinguish between different three phase connection,

determine the current, voltage and power in star and delta connected three
phase balanced circuits,

convert the star connection to delta and vice-versa, and

apply the maximum power transfer theorem and Thevenin theorem in ac and
dc circuits.

4.2 INTRODUCTION TO ALTERNATING

QUANTITY
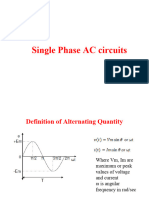
Quantity which varies periodically with time is known as the alternating quantity. It may
be voltage or current. Some waveform of alternating quantities are shown in Figure 4.1.

/2

(a) Sine Wave

f (t)

T/ 2

(b) Triangular Wave

f (t)

T/2

(c) Square Wave

82

Figure 4.1 : Alternating Waveforms

AC Circuits

4.2.1 Basic Definitions about the Alternating Quantity

Here we take the example of sinusoidal form of alternating current.
i = IM sin t

IM
0

/2

Figure 4.2 : Sinusoidal Waveform

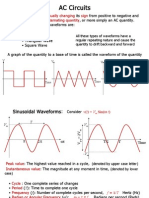
Cycle
It is the one complete set of positive and negative half of any alternating quantity.
Time Period
It is the time required in second to complete one cycle of any alternating quantity.
Frequency
Number of cycles per second is known as the frequency of alternating quantity. It
is the reciprocal of the time period and its unit is cycle per second or Hertz.
f = 1/T (in Hertz)
In India, the frequency of alternating supply is 50 Hertz, while in America and
Japan it is 60 Hertz.
Amplitude
It is the peak or maximum value of the alternating quantity. In Figure 4.2, Im
denotes the amplitude of the current wave.
Equation of Sinusoidal Alternating Quantity
The sinusoidal alternating current is written as
i = I m sin t

. . . (4.1)

Similarly, we can write for voltage

v = Vm sin t

where

. . . (4.2)

i, = Instantaneous value of current and voltage

Im, Vm = Maximum values
= 2f [f = frequency in Hz]
=

2
[T = Time period in sec]
T

. . . (4.3)

Phase
Phase of any alternating quantity shows the position of wave at any time after it
has passed through the zero position of reference.
Phase Angle
It is the angle of alternating quantity with respect to the reference position.
Phase Difference
When the maxima and minima of two sinusoidal alternating quantities (of same
frequency) do not occur at the same instant of time, then these two quantities are
said to have phase difference.
83

Electrical

(a) Reference Waveform

(b) Lagging Waveform by Angle

(a) Leading Waveform by Angle

Figure 4.3

Lagging Current by Angle

If the current waveform of Figure 4.3(a) is assumed to be reference wave, then
Figure 4.4(a) shows the lagging current.
i

Im
t

Figure 4.4(a) : Reference Current Waveform

i = I m sin (t )

. . . (4.4)

This equation shows that current is lagging (or running behind) the reference wave
by an angle .
Leading Current by an Angle
Figure 4.4(b) shows the leading current by an angle by the reference wave of
Figure 4.4(a).
i = I m sin (t + )

84

. . . (4.5)

AC Circuits

Im
t

Figure 4.4(b) : Leading Current Waveform

4.3 RMS AND AVERAGE VALUE

These two values represent the direct value (steady values) of any alternating quantity
and defined as :
RMS Value (Root Mean Square Value
The root mean square current is given by that equivalent steady (dc) current which
will produce the same amount of heat in a given circuit as could be produced by
the alternating current when flowing through the same circuit for the same time
period.
Consider the circuit shown in Figure 4.5. First we connect the Direct Source (DC)
to the resistor for the particular time t and find the heat i2 Rt joules. Then for the
same time t, we apply the alternating current from AC source v and again calculate
the heat transferred to the resistor. Now, the RMS value of current i is given by,
1
T

I rms =

[i (t )]2 dt

. . . (4.6)

T = Time period of current wave.

RMS value is also known as the effective or virtual value.

Figure 4.5 : A Typical Circuit

4.3.1 RMS Value of Complex Wave

Let the complex current is given by,

i = I 0 + I m1 cos t + im 2 cos 2t + I m3 sin t

2

Then the RMS value is given by

2

I rms =

I I
I
I 02 + m1 + m 2 + m3
2 2
2

. . . (4.7)
85

Electrical

4.3.2 Average Value

The average value of alternating current is defined by that steady value of current which
transfers the same amount of charge across any given circuit as could be transferred by
the alternating current for the same time.
I av =

1
T

. . . (4.8)

i (t ) dt

Note : Waveforms with half wave symmetry, i.e.

f (t ) = f t + T
2

where

T = time period.

Then the average value of such waves for the complete time period is zero (because
positive and negative halves are equal in one time period). For such waves, the average
value is computed over the positive half of the period. This is sometimes called the half
cycle average. (All the waveforms of Figure 4.1, have such symmetry).

4.3.3. RMS Value of Sinusoidal Wave

Consider the waveform of Figure 4.2. The time period is 2 radian, i.e. T = 2.
From Eq. (4.6) the RMS value is given by
T

1
I rms =
T

[i (t )]2 dt

Here, we integrate with respect to t or angle.

So,

I rms =

1
2
1
2
2
Im
2

2
Im
2

[i (t )]2 d (t )

2
Im
sin 2 t d (t )

1 cos 2t

d ( t )
2

1 cos 2t

2
sin t =

I
sin 2t

= m = 0.707 I m
t

2 0
2

. . . (4.9)

4.3.4 Average Value of Sinusoidal Wave

Since the waveform has the half wave symmetry the average value for time period
T = 2 will be zero. So the average value will be calculated for half time period.
From Eq. (4.8), the average value is given by
I av =

86

1
T

i (t ) dt =

I m sin t d (t )

I
2I
I
= m [ cos t ]0 = m = m = 0.637 I m

. . . (4.10)

AC Circuits

4.3.5 Form Factor

The form factor is defined as

Kf =

RMS value
Average value

. . . (4.11)

For sinusoidal wave,

Kf =

0.707
0.637

Im
= 1.1
Im

4.3.6 Peak, Crest or Amplitude Factor

Kf =

Maximum value
RMS value

. . . (4.12)

For sinusoidal wave,

I
K f = m = 2 = 1.414
Im
2

4.4 COMPLEX REPRESENTATION OF

ALTERNATING QUANTITIES
Alternating quantities are represented by complex number.
Rectangular or Cartesian Representation

Any alternating quantity can be represented in complex form with real and
imaginary part : Like
i = a + jb

= c + jd

. . . (4.13)

where j = 1 , which gives the rotation through 90o in anticlockwise direction,

a = real part, and
b = imaginary part.
Representation of Alternating Quantity on Complex Plane

In complex plane, x-axis represents the real axis (reference axis) and y-axis
represents the imaginary axis ( j-axis). Figure 4.6 shows the representation of
complex quantity on complex plane.
Im

a + jb
b
0

Figure 4.6 : Complex Plane

Re

87

Electrical

Polar Representation

Any alternating quantity can be represented in polar form (magnitude angle

form) as under

i = r1 1

= r2 2

. . . (4.14)

Rectangular to Polar Conversion

r1 = a 2 + b2
b
a

and

1 = tan 1

Also

r2 = c 2 + d 2

and

2 = tan 1

. . . (4.15)

d
c

. . . (4.16)

In this way, rectangular quantities a + jb and c + jd can be converted into

corresponding polar form, i.e.
r1 1

and

r2 2

In Figure 4.7

r1 = OA = a 2 + b 2
and 1 is the angle made of line OA from the horizontal axis are show,
A
r1
1

Figure 4.7

Polar to Rectangular Conversion

r1 1 can be written as :

r1 e j 1 ,

Then by Eulers theorem :

r1 e j 1 = r1 [ cos 1 + j sin 1 ]
= r1 cos 1 + j r1 sin 1

So,

a = r1 cos 1

and

b = r1 sin 1

. . . (4.17)

Example 4.1

Find RMS and average value of the output of half wave rectifier.
Solution

The waveform of current, output of the half wave rectifier is shown in Figure 4.8.

Figure 4.8

88

AC Circuits

Time period of wave = 2

RMS value of current

1 2
i d ( t ) + 0 d ( t )
2

0
0

I rms =

1
I m sin (t ) 2 d (t )
2

Im
(1 cos 2t ) d (t )
4

I
I rms = m = 0.5 I m
2
Average value of current
I av =

1
2

i d ( t ) =

1
2

I
I m sin t d (t ) = m

Example 4.2

Find the form factor and peak factor for the above half rectified wave.
Solution

From the above example,

I rms = 0.5 I m

I
I av = m

Form factor

and peak factor

I
0.5 I m
= rms =
= 1.57
Im
I av

Im
Im
=
=2
I rms 0.5 I m

Example 4.3

For the output of full wave rectifier, determine

(a)

RMS value,

(b)

Average value,

(c)

Form factor, and

(d)

Peak factor.

Solution

The output current of full wave rectifier is shown in Figure 4.9.

Figure 4.9

89

Electrical

Time period =
(a)

I rms =

I av =

i d ( t ) =

2
Im
2

I rms =

(b)

2
Im
sin 2 t d (t )

I
(1 cos 2 t ) d (t ) = m = 0.707 I m
2
0

I
2I

I m sin t d (t ) = m [1 cos t ]0 = m = 0.637 I m

(c)

I
0.707 I m
= 1.1
Form factor K f = rms =
I av
0.637 I m

(d)

Peak factor K p =

Im
Im
=
= 1.414
I rms 0.707 I m

Example 4.4

For the saw tooth wave shown in Figure 4.10, determine the form factor.

Figure 4.10 : Saw Tooth Wave

Solution

Time period of given wave is 2 sec. Expression of function f (t) for first time
period.

f (t ) =

10
t =5t
2

for 0 t 2

RMS Value
Frms =

Frms =

1
T

f 2 (t ) dt =

25 t 3
2 2

1
2

(5 t ) 2 dt =

25
2

t 2 dt

= 5.77
0

Average Value

1
Fav =
T

1
f (t ) dt =
2

5 r2
5t dt =
2 2

Form Factor

90

F
5.77
K f = rms =
= 1.154 .
5
Fav

=
0

5
(4) = 5
4

AC Circuits

SAQ 1
(a)

Find the rms and average value of the waveform shown in Figure 4.11,
where in the first interval f (t ) = 10 e 200 t . Also find the form factor.

Figure 4.11

(b)

Find the effective (or RMS) value for the average function.

v (t ) = 20 + 30 sin t + 60 sin 2 t
2

4.5 RESISTIVE, INDUCTIVE AND CAPACITIVE

CIRCUITS
AC through Pure Resistive Circuit

Applied voltage,

v = Vm sin t

. . . (4.18)

The resultant current, i

i=

V Vm
=
sin t = I m sin t
R
R

. . . (4.19)

Current, i is in phase with applied voltage, v. The waveforms and phasor diagram
are shown in Figures 4.12 and 4.13, respectively.

Figure 4.12 : Resistive Circuit

Figure 4.13 : Current and Voltage Waveforms

AC through Pure Inductive Circuit

The circuit is shown in Figure 4.14. Again the applied voltage is given by
v = Vm sin t

v=L

di
dt

91

Electrical

Now,

v = Vm sin t

Vm sin t = L

V
di = m sin t dt
L

di
dt

Figure 4.14 : Inductive Circuit

Integrating both sides, we get

V
i= m
L

sin t dt

V
V
= m ( cos t ) = m cos t
L
L
V

= m sin t
L
2

= m sin t
XL
2

. . . (4.20)

where XL = inductive reactance = L in ohm, if we put

Vm
= I m , then
XL

i = I m sin t
2

. . . (4.21)

Here, we can see that current lags the applied voltage by angle

. The waveform
2

and phasor diagram are shown in Figure 4.15.

(a) Waveform

(b) Phasor Diagram

Figure 4.15

AC through Pure Capacitor

The current passing through capacitor is given by

i=C
=C
92

dv
dt
dv
(Vm sin t )
dt

= C Vm cos t

. . . (4.22)

Vm

sin t +
XC
2

Xc =

where

AC Circuits

Vm

sin t +
1
2

C
. . . (4.23)

1
= Capacitive reactance in ohm.
C

Figure 4.16 : Pure Capacitive Circuit

If we put I m =

Vm
, then
XC

i = I m sin t +
2

. . . (4.24)

Here, we can see that current i leads the applied voltage by

.
2

The waveform and phasor diagram are shown in Figure 4.17.

(a) Waveform

(b) Phasor Diagram

Figure 4.17

4.5.1 Series RLC Circuit

The applied voltage is

v = Vm sin t

Inductive reactance

X L = L

Capacitive reactance

XC =

1
C

Figure 4.18 : Series RLC Circuit

93

Electrical

Here, we define the impedance of the circuit which is given by

Z = R + j ( X L X C ) in ohm

. . . (4.25)

The magnitude of the impedance is

| Z | = R 2 + ( X L X C )2
= tan 1

and angle

X L XC
R

This is the angle between the applied voltage v and the current i. is also known as the
power factor angle of the circuit.
The current i is given by
i=

=
Z

Vm sin t
R 2 + X 2 tan 1

X
R

where X = XL XC
or

V
X

i = m sin t tan 1
|Z|
R

. . . (4.26)

If the circuit in inductive (XL > XC) then current i lags the v by angle tan 1
circuit is capacitive then i leads the v by angle tan 1

X
. But if the
R

X
.
R

The voltage drop across each passive elements

VR = i R,
Also

VL = XL i,

VC = XC i

v = vR + vL + vC

(Kirchhoffs Voltage Law)

. . . (4.27)

In general, if we apply Kirchhoffs voltage law in series RLC circuit then KVL equation
is given by

v=Ri+L

di 1
+
dt C

i dt

. . . (4.28)

4.5.2 Parallel RLC Circuit

Now we connect passive elements R, L, C in parallel along with one current source.

Figure 4.19 : Parallel RLC Circuit

Since the circuit is parallel the voltage v across all the elements remain same. The source
current i is distributed along the three elements by Kirchhoffs current law.
i = iR + iL + iC

94

in general,

i=

v 1
+
R L

v dt + C

dv
dt

. . . (4.29)

AC Circuits

Here, we define conductance, susceptance and admittance.

Conductance G = Reciprocal of resistance

1
in mho ( )
R

Inductive susceptance

BL =

1
( )
XL

Capacitive susceptance

BC =

1
( )
XC

Admittance Y = Reciprocal of impedance

1
Z

. . . (4.30)

4.6 CONCEPT OF POWER

We know that power is defined as the time rate of doing work and is given by P.

P=

dw
dt

. . . (4.31)

dw dq

=vi
dq dt
Energy (Total work done) is given by
w=

P dt joules

or Watt-sec

. . . (4.32)

4.6.1 Power in AC Circuit

Power in AC circuit is classified as apparent power, active power and reactive power :
Apparent Power

Product of voltage and current. Its unit is volt-amp.

S = VI Volt-Amp
2

=I Z

. . . (4.33)

Apparent power is an important parameter in the specification of electrical

equipment, as the size and cost of many electrical machines depends on their
Volt-Amp rating rather than voltage rating.
Active Power or True Power

It is given by

P = VI cos Watt

. . . (4.34)

It is the power, which is actually consumed in any circuit. Its unit is Watt. The
above formula indicates that the power received by a load is not merely the
product of its rms values of its terminal voltage and current but includes an
additional multiplicative factor cos , called power factor of the load.
Reactive Power

It is the power taken by the reactance and its unit is volt-amp reactive (VAr).
It is given by
Q = VI sin VAr

. . . (4.35)

Q is called reactive power as it is associated with the reactive elements (LC)

and does not contribute to the net transfer of energy from the source to the
load.
95

Electrical

4.6.2 Power Triangle

All the three power S, P and Q can be represented in a triangle, called the power triangle
as shown in Figure 4.20.
P=V I cos

S=VI

S=VI

Q=V I sin

Q=V I sin

S=VI

P=V I cos
(a) For Lagging or Inductive Load

(b) For Leading or Capacitive Load

Figure 4.20 : Power Triangle

Power can also be represented in complex form.

S = P + jQ

. . . (4.36)

Magnitude S = P 2 + Q 2

4.7 POWER FACTOR

In the expression for power P = VI cos , the term cos is known as power factor, its
value lies between 0 to 1.
It may be defined as

Cosine of the angle of lead or lag between current phasor and voltage
phasor,

The ratio

True Power
Watts
=
Apparent Power Volt amperes

. . . (4.37)

The ratio

R Resistance
=
Z Impedance

. . . (4.38)

For a constant load power P and system voltage V, current and VI requirement vary
inversely as the load power factor. A lower value of p.f leads not only to enhanced cost
of power supply equipment but also to increased voltage drop and power losses in supply
lines due to the increased line current. High value of p.f is a desired operating condition
in power supply system.

4.8 QUALITY FACTOR (Q-FACTOR)

Q-factor is the reciprocal of the power factor of coil. It is the figure of merit, i.e. it should
be as large as possible for any coil (combination of resistance and inductance).

Q = 2
or

Q=

Maximum energy stored

Energy dissipated per cycle

1
Z
=
cos R

L=

. . . (4.39)
. . . (4.40)

R 2 + X L2
R

If R is very less as compared to XL, then

Q=
96

X L L
=
.
R
R

. . . (4.41)

AC Circuits

Example 4.5

In the given circuit, find the active, reactive and apparent power.
15

0.2H

i
o

2200 ;60Hz
Figure 4.21

Solution

The inductive reactance, XL = 2 fL

= 2 60 0.2
= 75.408
Impedance, Z = 15 + j 75.408
In polar form = 76.885 78.749o
Current in the Circuit

i=

v
220 0o
=
Z 76.885 78.749o

= 2.861 78.749o Amp (lagging)

Power factor cos = cos 78.749o
= 0.195 (lag)
sin = sin 78.749o

and

= 0.98
Active Power

P = VI cos
= 220 2.861 0.195
= 122.7 Watts
or

P=I R
= 122.7 Watts

Reactive Power

Q = VI sin
= 220 2.861 0.98
= 616.83 volt-Amp reactive
or

Q=I X
= 617.1 VA

Apparent Power

S = VI
= 220 2.861
= 629.42 Volt-amp
or

S = P2 + Q2
= 629.2 Volt-amp.

Example 4.6

97

Electrical

In series R-L circuit, shown in Figure 4.22, find

(a)

Impedance,

(b)

Resultant current,

(c)

Power factor and its nature, and

(d)

Quality factor.
R = 10

L = 0.1H

i
o

220 0 ; 50Hz
Figure 4.22

Solution

The inductive reactance XL is given by

XL = L
= 2 fL
= 2 50 0.1
= 31.42
The impedance in rectangular form is given by
Z = R + j X L = 10 + j 31.42

In polar form

Z = 32.97 72.345o

The resultant current is given by

i=

220 0o

=
Z 32.97 72.345o

= 6.672 72.345o Amp.

The current is lagging (since the circuit is inductive).

The power factor angle, , is the angle between voltage current
= 72.345o (lagging)

p.f. cos = cos (72.345o)

= 0.303 (lag)

Alternatively, the power factor can be determined by

cos =
=

R
Z

10
32.97

= 0.303 (lag)

Quality factor is given by Q =

98

Example 4.7

1
= 3.3 .
cos

An inductive coil of resistance 32 and reactance 15.7 is connected in series

with a capacitor of reactance 79.5 . The circuit is connected across 500 V AC
supply, determine
(a)

Current,

(b)

Phase difference between voltage and current,

(c)

Magnitude of voltage across the inductive coil, and

(d)

Total power absorbed.

AC Circuits

Solution
x2=15.7

R=32

xc=79.5

v = 500V

Figure for Example 4.23

R = 32 ,

X = XL XC

= 63.8 (circuit in capacitive)

Z = R jX = 32 63.8 j

Impedance
(a)

Current i =

v
500 0o
=
Z 32 63.8 j

= 7 63.36o Amp
(b)

Angle between V and i

= 63.36 (leading)

(c)

Impedance of coil, ZL = R + j XL = 32 + j 15.7

| Z L | = 35.6439

Voltage across coil = I ZL = 7 35.6439

= 249.5075 Volt
(d)

Power absorbed = I R = 7 32 = 1568 watts

Example 4.8

In the capacitive circuit of Figure 4.24, find

(a)

Impedance,

(b)

Resultant current,

(c)

Power factor,

(d)

Power absorbed by the circuit, and

(e)

Phasor relation between different voltages and currents.

VR

VC

R=120

C=1F

100V
50Hz
Figure 4.24

Solution

99

Electrical

(a)

The capacitive reactance is given by

1
1
=
C 2 fC

XC =

2 50 1 10 6

= 3182.68
So the impedance, Z = R j X C
= 120 j 3182.68
Z = 3184.94 87.84o

In polar form,
(b)

Resultant current
i=

v
100 0o
=
Z 3184.94 87.84o

= 0.03139 87.84o Amp (leading)

(c)

Power factor, cos = cos 87.84o

= 0.0376 (lead)

(d)

Power is absorbed by resistor only and that is also known as the active
power in the circuit
2

P=I R
= (0.03139)2 120
= 0.1182 Watts
(e)

Voltage drop across resistor :

VR = iR
= 0.03139 87.84o 120
= 3.7668 87.84o Volt (in phase with current i)
Voltage drop across capacitor
Vc = i ( j X c )

= 0.03139 87.84 3182.68 90o

= 99.9 2.16o (lagging)
The phasor diagram is shown in Figure 4.25 and applied Voltage of
100 0o is taken as reference.
VR

I
87.84

V=100V
V=VR+VC

2.16

VC

Figure 4.25 : Phasor Diagram

100

AC Circuits

SAQ 2
(a)

(b)

The current in a circuit is given by (4.25 + j 12) Amp, when applied voltage
is (100 + j 50) volt, determine
(i)

the complete expression for the impedance,

(ii)

power consumed,

(iii)

apparent power, and

(iv)

phase angle between the current and voltage.

A sinusoidal source of e (t) = 170 sin 377 t is applied to an R-L circuit. It is

found that the circuit absorbs 720 watts, when an effective current of
12 Amp flows.
(i)

find the power factor of the circuit,

(ii)

calculate the inductance in henry, and

(iii)

compute the value of impedance.

4.9 SERIES AND PARALLEL RESONANCE

Resonance is that condition in any AC circuit at a particular frequency, when the applied
voltage and resultant current are in same phase. So, at resonance the power factor of the
AC circuit is unity and it behaves like a pure resistive circuit.

4..91 Series Resonance

In series RLC circuit at a particular frequency when inductive reactance (XL = L)
1

becomes equal to the capacitive reactance X C =

, then the circuit is said to be at

resonance
XL = XC

. . . (4.42)

In the series RLC circuit of Figure 4.26, the circuit current I is given by
VR

VL

VC

I
V volts, f Hz

Figure 4.26 : Series Resonance Circuit

I =

V
A
Z

where Z represents the equivalent impedance of the circuit.

Z = R + j L +

1
j C

= R + j L

1
j
C

101

Electrical

Z = R + j (X L XC )

or

1
C

X L = L and X C =

where

= R + jX
where (XL XC) = X (Net Reactance)

I=

Thus

V
V
=
Amp
R + j ( X L X C ) R + jX
VL
o

90

VR

I
(across R)

(across L)
I

90
VC

(across C)

Figure 4.27 : Voltage and Current Phasor

And voltage drop across resistance, R is VR = IR (in phase with I)

Voltage drop across inductance, L is VL = I XL (leading I by 90o)
Voltage drop across capacitance, C is VC = I XC (leading I by 90o)
The phasor diagram of the variables of the entire circuit is shown in Figure 4.28.
VL

V
(VL Vc)

VR
VC

Figure 4.28 : Voltage Vector Diagram of RLC Series Circuit

Resonance condition is obtained when XL = XC in the series circuit (this is obtained by

either decreasing the supply frequency when XL would decrease and XC would increase or
by increasing the supply frequency making XL to increase and XC to decrease).
When

XL = XC, Z = R + jO = R

Also,

I0 =

V V
=
Amp
Z R

[I0 = Current at resonance]

The p.f. (power factor) of the circuit becomes

cos =

R R
= =1
Z R

The expression of frequency of resonance can be obtained as follows :

Let 0 or f0 be the frequency at which XL = XC.
i.e.
102

0 L =

1
0 C

. . . (4.43)

or

02 =

i.e.

f0 =

1
i.e. 0 =
LC

AC Circuits

1
rad/ sec
LC

. . . (4.44)

Hz

2 LC

Voltage vector diagram at resonance is shown in Figure 4.29.

VL
I

VC
Figure 4.29 : Voltage Vector Diagram at Resonance (VL = Vc)

Impedance Curve

Impedance

Figure 4.30 shows variation of impedance Z, inductive reactance XL and capacitive

reactance XC with frequency. At resonance XL = XC and Z = R.
X

XL = L

Xc = I/L

Figure 4.30 : Impedance Curve

Angle Curve
Angle (between voltage and current) is given by

= tan 1

(X L Xc )
R

. . . (4.45)

Here, is known as the power factor angle. Figure 4.31 shows the variation of
with frequency.
At frequencies below 0 the capacitive reactance is greater than the inductive
reactace and the angle of the impedance is negative. If the resistance is low, the
angle changes more rapidly with frequency as shown in Figure 4.31. As
approaches zero the angle of Z approaches 90.

+90

Low R
High R
0

-90

Figure 4.31 : Angle Curve

103

Electrical

Admittance Curve
Admittance Y is reciprocal of impedance. Its variation with frequency is shown in
Figure 4.32.

1
Z

. . . (4.46)

Admittance

Y =

Low R

High R
w0
Figure 4.32 : Admittance Curve

Resonance Curve

Figure 4.33 shows the variation of current with frequency. Current is maximum at
I
resonance frequency 0. At rms value of current 0 , power becomes half of its
2
I
maximum value. So the points, corresponding to 0 on the resonance curve, are
2
known as the half power points. Frequency 1 and 2 corresponding to these two
points are known as the lower and upper half power frequency.
I
I0
I0 /

(rad/sec)

Figure 4.33 : Resonance Curve

Band Width

The distance between upper and lower half power frequencies, measured in hertz
or in rad/sec, is called the banwidth BW.

or

BW = 2 1 in rad/sec.

. . . (4.47)

BW = f2 f1 in Hz

. . . (4.48)

The resonant frequency 0 is geometric mean of 1 and 2.

0 = 1 2 and f 0 =

f1 f 2

. . . (4.49)

4.9.2 Parallel Resonance

104

Figure 4.34 represents a parallel resonating circuit where a coil is connected in parallel
with a capacitor C and the combination is connected across an AC voltage source of
variable frequency. Figure 4.35 represents the vector diagram of the given circuit.

IC

AC Circuits

Coil
IL
R
I

V
AC .f Hz

Figure 4.34 : A Typical Parallel Resonating Circuit

IC

ILsin

ILcos

IL
Figure 4.35 : Vector Diagram of the Parallel AC Circuit

Let

IC = The current through the capacitor,

IL = The current through the coil,
I = Vector sum of IL and IC, i.e. the source current,
V = Supply voltage,
VR = Drop across R,
VL = Drop across L,
VC = Drop across C,
= p.f. angle of the coil (i.e. the angle of lag of IL with respect to V),
ZL = Coil impedance, and
XC = Capacitor impedance (or simple capacitor reactance).

Here

IC =

V
XC

And

IL =

V
=
ZL

cos =

. . . (4.50)
V
R 2 + X L2

V
R 2 + ( L ) 2

R
Z

At resonance the capacitive current must be equal to the inductive part of the coil current,
i.e. the imaginary components of IL and IC must cancel each other at resonance.
i.e.

I C = I L sin

or

X
V
V
=
L
XC ZL ZL

where
or

sin =

XL
,
ZL

Z L2 = X C X L

105

Electrical

Z L2 =

Also

1
0 C

L
, i.e. Z L =
C

0 . L =

L
C

. . . (4.51)

[0 represents resonance frequency]

R 2 + 02 L2 =

or
or

02 L2 =

i.e.

02 =

0 =

i.e.

f0 =

L
R2
C

1
R2

LC L2

1
R2 1

=
LC L2
L
1
2 L

L
C

L
R2
C

. . . (4.52)

L
R2
C

. . . (4.53)

If the resistance of the coil be neglected,

f0 =

1
2 L

L
1
=
C 2 LC

. . . (4.54)

Again, at resonance, since the reactive components of IL and LC balance each other, the
only remaining part of the current is IL cos (= I)
I = I L cos

or,

V
V
R
=
.
Z Z L Z L

or,

L
Z L2 C
L
=
=
Z =
R
R CR

[Z = equivalent impedance of parallel circuit.]

Z L =

. . . (4.55)

Then, the equivalent impedance of the parallel resonating circuit is L/CR at resonance.
This impedance is called dynamic resistance of the parallel circuit. Normally R being
loss, this impedance is very high at resonance and then the current is much lower in the
parallel circuit. Then, this circuit is also called rejector circuit.
Different Curves at Parallel Resonance

Figure 4.36 shows admittance (Y), impedance (Z) and power factor angle ()
curves, which show the variation of Y, Z and () with frequency.
(Y)

(Z)
o

+90

Admittance

Y Bc = C

Impedance

High R

Low R

BL = I/L

(a)

Low R

High R

(b)

-90

(c)

Figure 4.36

106

BC = C and BL =1/L are the capacitive and inductive susceptance.

B

Net susceptance

AC Circuits

B = BC BL
B

= C 1/L

. . . (4.56)

at resonance B = 0.
Resonance Curve

Since admittance is minimum or impedance is maximum at resonance frequency

C, so current I is also minimum at parallel resonance.
I, Z

Impedance Z =

L
CR

Leading p.f.

Lagging p.f.

Figure 4.37 : Resonance Curve for Parallel Resonance

Properties of Resonance of parallel RLC circuit

(a)

Power factor is unity.

(b)

Current at resonance is [V / (L / CR)] and is in phase with the applied

voltage. The value of current at resonance is minimum.

(c)

Net impedance at resonance of the parallel circuit is maximum and

equal to (L / CR) .

(d)

The admittance is minimum and the net susceptance is zero at

resonance.

(e)

The resonance frequency of this circuit is given by

f0 =

1
2

1
R2

LC L2

Example 4.9

Find the resonant frequency 0 (or f0) for the given series RLC circuit
10

2 Henry

20F

v = Vm sin t = 50 sin t
Figure 4.38

Also find the expression for resonant current.

107

Electrical

Solution

R = 10 , L = 2 Henry, C = 20 F
Under resonance :
XL = XC

1
C

L =

1
LC

0 =

and

f0 =

Current i is given by i =

2 20 10

1
2 LC

= 0.158 103

= 25.16 Hz

V
Z

But at resonance Z = R or 10
So

V sin t 50 sin t
i= m
=
= 5 sin t Amp
R
10

Example 4.10

Find the value of R, so that the condition for resonance is fulfilled

5j

-3j

Figure 4.39

Solution

Admittance of first branch

Y1 =

1
R 5j
mho ( )
=
R + 5 j R 2 + 25

Admittance of second branch

Y2 =

1
4 + 3j
=
mho ( )
4 3j
25

Total admittance of the circuit :

Y = Y1 + Y2 =

R 5j
2

R + 25

4 + 3j
25

According to condition of resonance the imaginary part of the admittance must be

zero
i.e.
108

5
2

R + 25

3
=0
25

R 2 + 25

AC Circuits

3
25

R = 4.082

Example 4.11
A circuit shown in Figure 4.40 having a resistance of 5 , an inductance of 0.4 H
and a variable capacitance in series is connected across a 110 V, 50 Hz supply.
Calculate :
(a)

The value of capacitance to give resonance

(b)

Current

(c)

Voltage across the inductance

(d)

Voltage across the capacitance

(e)

Q-factor of the circuit.

Solution
Applied Voltage, V = 110 V
Resistance, R = 5
Inductance, L = 0.4 Henry
Resonant frequency, f0 = 50 Hz
1

As Resonant frequency f 0 =

2 LC

0.4 H

110 V, 50 Hz
Figure 4.40

(a)

At resonant frequency capacitance

C=

1
4

f 02

=
L

1
2

4 (50)2 0.4

= 2.53303 10 5
= 25.3303 F
(c)

At resonant condition I =

V 110
=
.
R
5
= 22 A

(c)

Voltage across inductance = I XL = 22 2 50 0.4

= 2764.60 V.

(d)

Voltage across capacitance = Voltage across inductance

= 2764.60 V
109

Electrical

(e)

Q-factor =

0 L 2 f0 L
=
R
R
2 50 0.4
5

= 25.1327
Example 4.12
A 20 resistor is connected in series with a coil, a capacitor and an ammeter
across a 25 V variable frequency supply. When the frequency is 400 Hz, the
current is at its maximum value of 0.5 A and potential difference across the
capacitor is 150 V. Calculate :
(a)

Capacitance of capacitor, and

(b)

Resistance and inductance of coil.

R=20

RL

IM=0.5A A

VC=150V

25 V, 400 Hz
Figure 4.41

Solution
(a)

Let capacitance = C farad

Resonant frequency, f0 = 400 Hz
Capacitive reactance, X C =

1
1
1
=
=

C 2 400 C 800 C

Voltage across capacity = Im XC = 150 V

Im = 0.5 A

0.5
= 150
800 C
C=

or
(b)

0.5
= 1.3263 10 6 F
800 150

C = 1.3263 F

Let, RL and L be the resistance and inductance of coil respectively

Current, I m =

0.5 =

V
R + RL

25
( Applied voltage V = 25 V)
20 + RL

RL = 30
110

AC Circuits

SAQ 3
(a)

A series RLC circuit has a resonant frequency of 220.6 Hz and is fed from
125 V source. At resonance the voltage across inductance and capacitance is
4151 Volt. The resistance of circuit is 1.06 . Find QLC of the circuit.

(b)

A coil of inductance 0.75 H and resistance 40 is a part of a series resonant

circuit having a resonant frequency of 55 Hz. If the supply is
250 V, 50 Hz. Find

(c)

(i)

current,

(ii)

power factor, and

(iii)

voltage across the coil.

Determine R1 and R2 which cause the circuit shown in Figure 4.42 to be

resonant at all frequencies.

Figure 4.42

4.10 THREE PHASE AC CIRCUIT

Alternating circuits so far discussed have single phase supply system and its satisfactory
for domestic application like light, fan and heating, etc. But for industrial applications
and large size electrical devices, etc. 1-phase system has many limitations. Hence,
polyphase system (2-phase, 3-phase and 6-phase systems) are used in electrical
engineering. But for generation, transmission and distribution and utilisation of electrical
power a 3-phase system has been universally adopted. 2 and 6-phase are derived from the
3-phase system, if required.
A set of three single phase sinusoidal voltage currents of same frequency and magnitude
2
radians electrical constitutes
but have a progressive phase difference of 120o or
3
balanced 3-phase voltage/current.

Figure 4.43(a) : Phasor Diagram

111

Electrical

(b) Wave Diagram of 3-Phase Voltage

Figure 4.43 : Three-phase Voltage System

Figure 4.43 shows that 3-phase voltage and their instantaneous values are given by,
Vaa = Vm sin

Vbb = Vm sin ( 120o )

= Vm sin t

Vcc = Vm sin ( 240o )

= Vm sin t

Wave diagram is shown in Figure 4.43(b).

For a general n-phase system displacement between phases is given by
so for 2-phase system it is 90o electrical.

360o (electrical)
,
n

General Notations used in 3-phase

In three phase circuits, the phases are normally identified by the colours of
insulation on wires used, i.e. R for red, Y for yellow and B for blue. Often the
phases are also marked as A, B, C or 1, 2, 3. These nomenclatures, i.e. R-Y-B,
A-B-C or 1-2-3 are universally accepted.
The voltage in circuit VRY is positive from R to Y. the order of the subscripts
denoting the direction of the voltage. So
VRY = VYR

Similarly,

I RY = IYR

This form of double subscript notation makes the calculations in 3-phase circuits
simple and less ambiguous.
Phase Sequence
Phase sequence is the sequence or order in which the three current/voltages attain
their maximum values one after the other.
Let the three phases, Vaa , Vbb , and Vcc shown in Figure 4.44 refers phase A, B and
C, respectively. Then for the waveform shown A-B-C is the phase sequence. Since
only two directions, i.e. anticlockwise and clockwise of rotations are possible, only
two types of phase sequence are possible. By convention phase sequence ABC or
RYB is taken as positive and ACB or RBY as negative.
112

AC Circuits

(a) Positive Sequence

(b) Negative Sequence

Figure 4.44

Correct phase sequence is required when the machines are to be operated in

parallel, otherwise large circulating currents will flow.

4.10.1 Connection in Three-Phase System

The three elements, i.e. three phases of 3-phase source or three impedances of 3-phase
load can be inter-connected in two different ways called
(a)

Star connection, and

(b)

Delta connection.

In star connection similar ends the 3-phases are jointed together to form the neutral as
shown in Figure 4.45(a), star connection is denoted by Y and the common or neutral
point is denoted by n, it is also called star point.

(a) Star Connection

(b) Delta Connection

Figure 4.45

In delta connection three-phases are connected in series, end-to-end to form a closed

mesh as shown in Figure 4.45(b). Two dissimilar ends are joined together. Delta
connection is denoted by .
It can be shown that for 3-phase balanced system, the sum of instantaneous values of
currents or voltages is always zero. Let instantaneous 3-phase voltages of a balance
system are represented by :
Va = Vm sin t

Vb = Vm sin ( 120o )

. . . (4.57)

Vc = Vm sin ( 240o )

then, at any instant,

va + vb + vc = Vm sin t Vm sin (t 120o ) + Vm sin (t 240o )

113

Electrical

= Vm [sin t + sin (t 120o ) + sin (t 240o )]

= Vm [sin t + 2 sin (t 180o ) cos 60o ]
= Vm [sin t 2 sin t cos 60o ]

=0

. . . (4.58)

Similarly, for 3-phase currents of a balance system, we can show that

ia + ib + ic = 0

. . . (4.59)

This is the important property of 3-phase balanced system which has made possible the
star and delta connection of three phases, without any circulating currents.

4.10.2 Voltage, Current and Power Relations

In Star Connection
Vph = Phase voltage
VL = Line voltage
Iph = Phase current
IL = Line current

Figure 4.46

In star connection

VL = 3 V ph

. . . (4.60)

I L = I ph

. . . (4.61)

P3 = 3 VL I L cos Watts
= 3 V ph I ph cos

. . . (4.62)

where cos = Power factor.

In Delta Connection
VL = V ph

I L = 3 I ph
P3 = 3 VL I L cos Watts
= 3 V ph I ph cos
114

. . . (4.63)

AC Circuits

Figure 4.47

Star-Delta Connection

Figure 4.48

4.10.3 Conversion from Star Connection to Delta Connection

From the Star Connection
Resistance between terminals 1 and 2 when 3 is open circuited :

R12 = R1 + R2

. . . (4.64)

Figure 4.49

Similarly, resistance between terminals 2 and 3 when terminal one is open

circuited.

R23 = R2 + R3

. . . (4.65)

In the same way resistance between terminals, 1 and 3 is

R13 = R1 + R3

. . . (4.66)
115

Electrical

Figure 4.50

From the Delta Connection

Resistance between terminals 1 and 2 when 3 is open circuited.
Rc and Rb are in series. This combination is in parallel to Ra.

R12 =

Ra ( Rb + Rc )
Ra + Rb + Rc

. . . (4.67)

Figure 4.51

Similarly, the resistances between terminals 2 and 3 and 1 and 3 are given by :

R23 =

( Ra + Rc ) Rb
Ra + Rb + Rc

. . . (4.68)

R13 =

( Ra + Rb ) Rc
Ra + Rb + Rc

. . . (4.69)

Now compare the results of star and delta connections :

R1 + R2 =

Ra ( Rb + Rc )
Ra + Rb + Rc

. . . (4.70)

R2 + R3 =

Rb ( Ra + Rc )
Ra + Rb + Rc

. . . (4.71)

R1 + R3 =

Rc ( Ra + Rb )
Ra + Rb + Rc

. . . (4.72)

After solving the Eqs. (4.70), (4.71) and (4.72) we can determine three unknown
resistances Ra, Rb and Rc in terms of R1, R2 and R3.

R R + R2 R3 + R3 R1
Ra = 1 2
R3

. . . (4.73)

R R + R2 R3 + R3 R1
Rb = 1 2
R1

. . . (4.74)

R R + R2 R3 + R3 R1
Rc = 1 2
R2

. . . (4.75)

Eqs. (4.73), (4.74) and (4.75) are the desired results.

116

AC Circuits

4.10.4 Conversion from Delta Connection to Star Connection

Now we have to find R1, R2 and R3 in terms of Ra, Rb and Rc.
Ra, Rb, Rc Known resistances.
R1, R2, R3 Unknown resistances.
Again solving the Eqs. (4.70). (4.71) and (4.72) we can determine the resistances of star
connection, i.e. R1, R2, and R3.

R1 =

Ra Rc
Ra + Rb + Rc

. . . (4.76)

R2 =

Ra Rb
Ra + Rb + Rc

. . . (4.77)

R3 =

Rb Rc
Ra + Rb + Rc

. . . (4.78)

Table 4.1 : Comparison between Star and Delta Connected Systems

Sl. No.
1.

2.

3.

Star (Y) Connected System

In star connected system there is
common point known as neutral n or
star point. It can be earthed.
In star connected system we get 3-phase,
three wire system and also 3-phase, 4
wire system is taken out.

Delta () Connected System

There is no neutral point in delta
connected system

Line voltage VL = 3 V ph

Line voltage = Phase voltage

or,
4.

Only 3-phase, 3 wire system is possible

in delta connected system

VL = V ph

1
V ph =
VL
3

Line current = Phase current

Line current I L =

I L = I ph

I ph =

5.

Three phase power =

3 VL I ph cos

= 3 V ph I ph cos

3 I ph

1
3

Three phase power =

IL

3 VL I L cos

= 3 V ph I ph cos

Example 4.13
Obtain the equivalent inductance at terminal AB in circuit shown in Figure 4.52.

Figure 4.52

Solution
Inductances also follow the same rule as the resistances for series, parallel and stardelta connections. First we convert the star connection a b c n to corresponding
delta connection.

117

Electrical

Figure 4.53

For delta connection,

L L + Lbn Lcn + Lcn Lan

Lab = an bn
Lcn
=

1+1+1
= 3H
1

Similarly, Lbc = 3 H and Lac = 3 H

Figure 4.54

So, the circuit of Figure 4.52 is redrawn as shown in Figures 4.54 and 4.55.

Figure 4.55

So,

Leq =

3
H is in parallel with 3 Henry.
2

Leq =

1.5 3
= 1 Henry
1.5 + 3

Example 4.14
A balanced star connected load is supplied from a symmetrical 3-phase 440 Volt
system. The current in each phase is 40 Amp and lags 30o behind the phase
voltage. Find

118

(a)

phase voltage,

(b)

power,

(c)

reactive power drawn by a the load, and

(d)

phase impedance.

AC Circuits

Solution
For three phase star connected load voltage applied VL = 440 Volt
(a)

V ph =

440
= 254.03 Volt
3

Power current = I ph = 40 30o Amp = I L

(b)

Power P3 = 3 VL I L cos
= 3 440 40 cos 30o

= 26400 Watt = 26.4 kW

(c)

Reactive power drawn by the load :

Q3 = 3 VL I L sin
= 3 440 40 sin 30o

= 15242.047 Var = 15.24 kVAr

(e)

Phase impedance Z ph =

V ph
I ph

254.03 0o
40 30o

= 6.35 30o

Example 4.15
A delta connected balanced 3-phase load is supplied from a 3-phase 400 V supply.
The line current is 30 Amp and the power taken by the load is 10 kW. Find
(a)

impedance in each branch,

(b)

the phase current,

(c)

power factor, and

(d)

power consumed if the same load is connected in star.

Solution
Delta Connection Load
Line current IL = 30 Amp
Phase current I ph =
(a)

30
= 17.32 Amp
3

Phase impedance Z ph =

V ph
I ph

400 V
17.32 Amp

= 23.095
(b)

Phase current Iph = 30 Amp (already calculated)

(c)

Total 3-phase power = 10 kW

But 3-phase power = 3 VL I L cos

cos =

P
=
3 VL I L

10 1000
3 400 30

= 0.4811
(d)

The same power will be consumed if load is delta connected, i.e.

10 kW.
119

Electrical

SAQ 4
(a)

(b)

A balanced star connected load of (8 + 6j) ohms per phase is connected to a

3-phase, 230 V supply. Find the
(i)

line current,

(ii)

power, and

(iii)

power factor.

Three inductive coils each with a resistance of 15 and an inductance of

0.03 Henry are connected in star to a 3-phase, 400 V, 50 Hz supply.
Calculate
(i)

phase current and line current, and

(ii)

total power absorbed.

4.11 MAXIMUM POWER TRANSFER THEOREM

This theorem is used to determine the value of load, for which source will transfer the
maximum power. Before applying the maximum power transfer theorem, we apply
Thevenin theorem across load terminals. Now there are following three cases for load to
receive the maximum power.
Case I : Load is Pure Resistive
Now we have to find load resistance RL so that maximum power is transferred to it.

Figure 4.56 : Pure Resistive Load

Load current iL :

iL =

VTH
( RTH + RL ) + j X TH

| iL | =

VTH
2
( RTH + RL ) 2 + X TH

Power delivered to load RL.

PL = | iL |2 RL =

Condition for maximum power

dPL
=0
dRL
120

2
VTH

2
( RTH + RL )2 + X TH

RL

AC Circuits

( R + R )2 + X 2 R 2 ( R + R )
TH
L
TH
L
TH
L
2
VTh =
=0

2
2
(
R
R
)
X
+
+
TH
L
TH

2
( RTH + RL ) 2 + X TH
= 2 RL ( RTH + RL )

2
RL2 = RTH
+ X T2H

or,

2
2
RL = RTH
+ X TH

= | ZTH |

. . . (4.79)

So load resistance RL should be equal to the magnitude of the internal impedance

of circuit.
Case II : Load is Complex (Impedance)
Load current

VTH
( RTH + R) + j ( X TH + X )

iL =

. . . (4.80)

Figure 4.57 : Complex Load

Magnitude of load current

| iL | =

Load power

VTH

( RTH + R ) 2 + ( X TH + X ) 2

PL = | iL |2 R

2
VTh

( RTH + R)2 + ( X TH + X ) 2

For getting the maximum power of PL, denominator of equation should be small.
For that select X = Xth.
2
VTh

Then

PL =

dPL
= 0 R = RTH
dl

( RTH + R)2

So, for maximum power factor

Z = RTH j X TH = ZTH (Complex conjugate of ZTH)

. . . (4.81)

Maximum Power Transfer in Case of DC Network

Figure 4.58, shows the DC network for maximum power transfer. The load current
is given by

iL =

VTH
RTH + RL

121

Electrical

Power delivered to load

PL = iL2 RL =

2
VTH

( RTH + RL )2

RL

Figure 4.58 : DC Network

Condition for maximum power

dPL
=0
dRL

. . . (4.82)

RL = RTH

. . . (4.83)

So load resistance should be equal to the internal resistance of circuit for receiving
the maximum power.
The maximum power from equation
2
VTh

Pmax =

V2
RL = TH
4 RL
( RL + RL )2

Pmax =

2
VTH
4 RTH

. . . (4.84)

Maximum power transfer theorem is useful in communication network and

electronic circuits where demand of maximum power is important rather than the
efficiency. The overall efficiency of a network supplying maximum power to any
branch is only 50%. So use of maximum power transfer theorem is limited in
electrical and distribution networks where aim is high efficiency not the maximum
power.
As stated earlier, before applying the maximum power transfer theorem, we assure
that circuit should be in Thevenins equivalent form. So, here we define the
Thevenin theorem and then draw the Thevenins equivalent circuit.
Thevenin theorem states that any linear bilateral network across its load terminal
can be replaced by simple network having one voltage source (VTH) and one series
impedance (ZTH).
Thevenins Equivalent Circuit

Figure 4.59 : Thevenins Equivalent Circuit

122

where

VTH = Thevenins equivalent voltage

AC Circuits

= VOC = Open circuit voltage across the load terminals.

ZTH = Thevenins equivalent impedance
= Drive point impedance across the load terminals when
all the sources replaced by their internal resistances.
Example 4.16
Find the value of load resistance, RL for which the source will transfer the
maximum power. Also find the value of maximum power.

Figure 4.60

Solution
First we apply the Thevenin theorem and draw the Thevenins equivalent circuit.
Remove the load resistance RL.

Figure 4.61

Calculation for VTH :

VTH = Open circuit voltage across load terminals AB, and
= VAB

Figure 4.62

V AB = VTH

= 5 + 4i
123

Electrical

10
=5+4
6
= 1.66 Volt
Calculation for RTH :
Replace all the sources by internal resistance. (Internal resistance of ideal
voltage source is zero)

Figure 4.63

RTH = R AB

= 2 // 4 + 6

24
+6
2+4

= 7.33
Thevenins Equivalent Circuit
According to maximum power transfer theorem
RL = RTH = 7.33

iL =

1.66
= 0.1132 Amp
7.33 + 7.33

Figure 4.64

Maximum power

Pmax = iL2 RL

= 0.09398 Watts
= 93.98 m Watts
Example 4.17
Find the load for which the source will transfer the maximum power if load is
connected across the terminal A and B, under the following conditions :

124

(a)

load is resistive, and

(b)

load is complex

AC Circuits

Figure 4.65

Solution
Calculation for VTH

i=

20 0o
= 1.692 + 0.461 j Amp
11 3j

VTH = V AB = i (6 3 j ) = 11.53 2.3 j Volt

Figure 4.66

Calculation for ZTH

ZTH =

5 (6 3 j )
= 2.88 0.576 j
11 3 j

Figure 4.67

Thevenins Equivalent Circuit

Case I
Load is resistive, then value of load resistance will be equal to
magnitude of ZTH.
RL = | ZTH |

= (2.88)2 + (0.576)2 = 2.93

Case II
Load is complex :
Z L = ZT*H

(Complex conjugate of ZTH)

= 2.88 + 0.576 j
125

Electrical

Figure 4.68

SAQ 5
Determine the value of load ZL such that the maximum power is transferred for the
network shown in Figure 4.69. Also find the value of maximum power in watts.

Figure 4.69

4.12 SUMMARY
This unit describes the basic concepts of single and three-phase ac system. Unit provides
the detailed analysis and derivations as needed by topics. Here we determine the voltage
current power and power factor for resistive, inductive and capacitive circuits. Also we
apply Kirchhoffs voltage and current laws in series and parallel RLC circuit. Complete
analysis of balanced three-phase circuit along with the star-delta conversion is given in
the unit. Also the proper comparison is done between star connection and delta
connection.
A very detailed description of series and parallel resonance is given in the unit with all
important characteristics. Different curves like impedance curve, angle curve, admittance
curve, and resonance curve are drawn for both types of resonance.
At the end of the unit maximum power transfer theorem is stated for both ac and dc
circuit. Since the concept of Thevenin theorem is required for applying the maximum
power transfer theorem so same is also defined in the unit.

4.13 ANSWERS TO SAQs

SAQ 1
(a)

RMS value Frms =

=
126

1
T

[ f (t )]2 dt

1
0.005

0.05

[10e 200 t ]2 dt = 5 = 2.24

Average value Fav

1
=
T

1
f (t ) dt =
0.05

0.05

10e

200 t

AC Circuits

dt

Fav = 1

Form factor =
(b)

Frms
= 2.24
Fav

The effective or RMS value of v (t) can be determined by equation.

Vrms

30
60
= (20) +
+

2
2
2

= 400 + 450 + 1800 = 51.478 Volt

SAQ 2
(a)

Z
i

Figure for Answer to SAQ 2(a)

Here = 100 + j 50 Volt

i = 4.25 + j 12 Amp
Impedance, Z =

v
= 6.3247 j 6.0933
i

Impedance is capacitive as reactive component is negative.

Power

S = VI * = (P + jQ)
= (100 + j 50) (4.25 j 12)
= 425 + j 212.5 j 1200 + 600
= 1025 j 987.5
= 1423.299 43.9325o

Active power, P = 1025 Watts = Power consumed

Reactive power, Q = 987.5 Var (Capacitive)
Apparent power = 1423.299 VA
Angle between current and voltage = 43.93o.
(b)

Applied voltage = 170 sin 377 t

= 170 0o Volts
Current, I = 12 Amp,
Power, P = 720 Watts
Current resistance = R
2

P=I R
R=
But

P
I

720
(12) 2

=5

P = VI cos
127

Electrical

P
720
=
= 0.35294
VI 170 12

cos =

P.f.

= 69.33275o

V 170
=
= 14.1667
I
12

Impedance =

Reactance = XL

tan =

XL
Z

XL = 37.556
=L

L=

XL
= 99.61 mH

SAQ 3
(a)

R=1.06

125V, 220.6 Hz
Figure for Answer to SAQ 3(a)

At resonance, I =
given that

125 125
=
= 117.92 Amp
R
1.06

I XL = I 2 fL = 4151 volt

4151
4151
=
= 0.0254 H
I 2 f 117.92 2 220.6

L=

f =

2 LC

f2 =

1
2

4 LC

C=

C = 20.5 10 6 F

Quality factor, Q =
(b)

R=40

WL 2 f L
=
= 33.2
R
R
L=0.75 H

250V, 50 Hz
Figure for Answer to SAQ 3(b)

128

Resonance frequency, f0 = 55 Hz

1
2

4 L f 2

AC Circuits

Let capacitance = C Farad

f0 =

1
2 LC

C =

1
2

(2) f 02 L

C = 11.165 F

Applied voltage = 250 V, 50 HZ

XL = 2 fL
= 2 50 0.75 = 235.6194
Reactance of capacitance, X C =
XC =

1
2 fC

1
2 50 11.165 10 6

= 285.096

Total Impedance = (40) 2 + (235.6194 285.96) 2 = 63.6234

250
V
=
= 3.9294 Amp
63.6234
Z

(i)

Line current, I =

(ii)

Power factor =

(iii)

Voltage across coil I XL = 3.9294 235.6194

R
40
=
= 0.6287 (leading)
Z
63.6234

= 925.8429 Volt.
(c)

For the given parallel circuit, the resonant frequency is given by

0 =

L CR12

2
L CR2

1
LC

Now 0 can assume any value provided R12 = R22 =

In present case,

L
C

L
2 10 3
=
= 25
C 80 10 6
R1 = R2 = 5 .

SAQ 4
(a)

Line voltage = 230 Volt

In star connection phase voltage
V ph =

230
3

= 132.79 Volt

Per phase impedance of load

Z ph = (8 + 6 j ) = 10 36.87o
Phase current
I ph =

V ph
Z ph

132.79
10 36.87o

= 13.279 36.87o Amp

129

Electrical

(i)

In star connection I ph = I L = 13.279 36.87o Amp

(ii)

Three-phase power = 3 VL I L cos

= 3 230 13.279 cos ( 36.87)
= 4232 Watt

(iii)
(b)

Power factor = cos = 0.8.

Pre-phase load
Resistance R = 15 , inductance L = 0.03 H
Reactance of coil
X L = L = 2 50 0.03 = 9.42

Per phase impedance of load

Z ph = R + j X L = 15 + j 9.42 = 17.71 32.12o
Power factor = cos 0.847
Supply voltage = 400 V (3-phase)
(i)

Phase voltage V ph =

400
3

= 230.94 Volt

Phase current = Line current =

(ii)

V ph
Z ph

230.94
= 13.04 Amp
17.71

Total power absorbed

P = 3 VL I L cos
= 3 400 13.04 0.847
= 7652.12 Watts

SAQ 5
(a)

Calculation for VTH :

Figure for Answer to SAQ 5 (a)

VTH = V AB = 4 i

30 20o
=4
3j+4

= 22.96 6.96 j = 24 16.86o Volt

130

(b)

AC Circuits

Calculation for ZTH :

Figure for Answer to SAQ 5(b)

ZTH =

4 (3 j )
5 j = 1.44 3.08 j
4+3j

Thevenins Equivalent Circuit

For maximum power transfer, the load impedance ZL is complex
conjugate of ZTH.

Figure for Answers to SAQ 5(c)

*
Z L = ZTH

= 1.44 + 3.08 j
Power will be dissipated in resistive part only.
iL =

VTH
24 16.86o
=
Z L + ZTH
1.44 + 1.44

= 8.33 16.86 Amp

Pmax = | iL |2 1.44

= 99.92 Watts

131