1

MAE 3113
MEASUREMENTS AND INSTRUMENTATIONS
Fall 2014
Sampling, FFT, and Filtering Review Questions
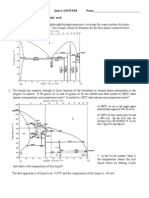
Given: A pressure transducer is used to measure the periodicity of a fluid flow.
The transducer output ranges from -5 to 5 volts, and the maximum frequency of
interest is 10 Hz. Superimposed on the signal is some pesky electronic noise at 60
Hz with an amplitude of 0.1 volts (the noise ranges from -0.1 to + 0.1 V). The
noise must be reduced by at least a factor of 10 (a gain of 0.1 or less). The cutoff
frequency to be used by the filter is 10 Hz.
(a) To do: Assuming that the only filters available are first, second, and fourthorder (n = 1, 2, or 4) Butterworth filters, select the lowest order filter that will
do the job
(b) To do: For the filter selected in Part (a), calculate the gain in dB right at the
cutoff frequency.
(c) To do: Notice from the problem statement that the cutoff frequency of the filter
is equal to the frequency of the signal. As calculated in Part (b), the amplitude
of the signal itself is therefore attenuated somewhat. To correct this problem,
you decide to use a second-order low-pass Butterworth filter, but with a higher
cutoff frequency. Calculate the highest cutoff frequency that can be used such
that it still provides the desired attenuation of the high frequency noise.
(d) To do: What is the minimum sampling frequency that should be used to avoid
aliasing (of the desired signal, not the noise)?
(e) To do: If we sample at 25 Hz, at what frequency will a small peak appear in the
spectrum due to the electronic noise?
Solution:

Given: A voltage contains a strong component at 1000 Hz (the desired signal),

along with some undesired noise at 12,000 Hz. Samantha puts in a first-order, lowpass, anti-aliasing filter with a design cutoff frequency of 2000 Hz, and then
digitally samples the voltage at a sampling frequency of 10,000 Hz.
(a) To do: Assuming Calculate the gain and decibel gain of the filter at both the
signal frequency and the noise frequency.
(b) To do: In order to meet specifications, the noise must be attenuated by at least
45 dB. What is the lowest-order filter that Samantha could buy to satisfy the
requirements: second-order, fourth-order, sixth-order, or eighth-order?

Given: A voltage signal ranges from -1.1 to 1.2 volts. A digital data acquisition
system is to be chosen four choices are available:
(a) 12 / = 10 10
(b) 8 / = 2 2
(c) 10 / = 5 5
(d) 14 / = 1 1
To do: Determine which system is the best choice for this application, assuming
that cost is irrelevant (all four are available in the lab).
Solution:

Given: A voltage signal contains frequency components at 150, 350, and 700 Hz.
It also contains some electronic noise at 60 Hz. We sample the data digitally at a
sampling frequency of 400 Hz.
To do: Is there any aliasing? If so, what frequencies will we see (perceive)?
Solution:

Given: Andy collects data with a digital data acquisition system that is 14-bit and
has a range of -5 to 5 V. He samples at a sampling frequency of 200 Hz.
(a) To do: Calculate the quantization error in millivolts.
(b) To do: For each case, will Andys signal be clipped? Is there any aliasing? If
so, what frequencies will he see (perceive)?
(a) Signal has a frequency of 40 Hz with a range of 3 to 3 V.
(b) Signal has a frequency of 120 Hz with DC offset = 4.5 V and amplitude =
1.0 V.
(c) Signal is () = 3.5(700 ) + 1.0 Volts.

Given: Voltage data are acquired with a digital data acquisition system. A FFT is
performed, and a frequency spectrum plot is generated.
To do: Which of the following has the better frequency resolution?
Case a: Data are sampled at fs = 100 Hz, and 512 data points are taken.
Case b: Data are sampled at fs = 200 Hz, and 256 data points are taken.

Given: Voltage data are acquired with a digital data acquisition system at =
1000 2048 data points are taken, a FFT is performed, and a frequency
spectrum plot is generated.
(a) To do: Calculate the total sampling time
(b) To do: Calculate the folding frequency of the resulting frequency spectrum
(c) To do: Calculate the frequency resolution of the resulting frequency
spectrum

Given: A voltage signal has a 1.50 V DC component and two periodic

components:
Frequency f1 = 115 Hz, amplitude A1 = 2.00 V
Frequency f2 = 540 Hz, amplitude A2 = 0.500 V
There is also some noise.
The signal is sampled at 1000 Hz, taking 256 data points.
(a) To do: Sketch the ideal frequency spectrum assuming sampling rate is not an
issue.
(b) To do: Is there any aliasing? If so, calculate fa.
(c) To do: Calculate the frequency resolution and sketch the frequency spectrum.
Solution:

Given: A voltage signal contains useful data up to about 1000 Hz. There is also
some unwanted noise at frequencies greater than 3000 Hz. We want to use a lowpass filter so that the noise is attenuated by at least 95%. We plan to use a cutoff
frequency of 2000 Hz so that there is minimal attenuation of the 1000 Hz
component of the signal.
To do: Calculate the required order of the low-pass filter.
Solution:

10

Given: Vibrations around 90 Hz with an amplitude of about 5 V are measured with

a DAQ. Data is sampled at fs = 500 Hz. Unfortunately, there is also some electronic
interference noise at 3600 Hz, with an amplitude of about 1 V.
(a) To do: Sketch the frequency spectrum that you would expect to see if there is no
filtering.
(b) To do: Sketch the frequency spectrum that you would expect to see after the
signal is filtered with a 4 -order low-pass anti-aliasing filter set to a cutoff
frequency of 200 Hz
Solution: