QG Course Manual January 2008 Version 5.1

A p p l i e d
Geost at i st i c s

f or Geol ogi st s & Mi ni ng Engi neer s
J ohn Vann

QG
Quantitative Group
Our Skills On Your Team
www.qroup.net.au
II
III
IV
I
Estimated
Block Z*V
True
Block ZV
Y=X
Y=X
Regression
of Y|X
Regressi on
of Y|X
m
e
a
n
Cut off
ZC
mean
C
u
t o
ff
Z
C
II
III
IV
I
Estimated
Block Z*V
True
Block ZV
II
III
IV
I
Estimated
Block Z*V
True
Block ZV
Y=X
Y=X
Regression
of Y|X
Regressi on
of Y|X
m
e
a
n
Cut off
ZC
mean
C
u
t o
ff
Z
C
Quantitative Group Short Course Manual
i

Copyright
2001, 2003, 2004, 2005, 2007, 2008
This document is copyright. All rights are reserved. No part of this document
may be reproduced, stored in a retrieval system, or transmitted in any form or by
any means, electronic, mechanical, photocopying, recording or otherwise, without
the prior written permission of Quantitative Geoscience Pty Ltd (trading as
Quantitative Group and QG).
Preliminary Edition September 2001
Second Edition January 2003
Third Edition January 2004
Third Edition with Minor revisions June 2005, December 2005
Fourth edition February 2007
Fourth Edition with minor revisions January 2008

Additional, inexpensive, bound copies of this manual can be obtained by contacting QG.
PO Box 1304, Fremantle
Western Australia 6959
info@qgroup.net.au
tel +61 (0) 8 9433 3511
fax +61 (0) 8 9433 3611

QG
Quantitative Group
ABN 30095494947
Our Skills On Your Team
www.qgroup.net.au

1

Cont ent s
COPYRIGHT I
CONTENTS 1
1: INTRODUCTION 7
ACKNOWLEDGEMENTS 8
PREREQUISITES 8
2: RESOURCE ESTIMATION CONCEPTS 9
DECISION MAKING AND RESOURCE ESTIMATION 9
SAMPLE QUALITY 10
GEOLOGY 11
OTHER FACTORS 11
ESTIMATION AT DIFFERENT STAGES OF A PROJ ECT 11
First Evaluation (Reconnaissance) 11
FIRST SYSTEMATIC SAMPLING 12
Precision and Accuracy 12
Sample Type 13
Resource Classification 14
Recoverable Resources at the Early Stage 14
INFILL SAMPLING 15
LOCAL ESTIMATION OF IN SITU RESOURCES 15
ESTIMATION OF RECOVERABLE RESOURCES 17
"Support" of the Selection Units 18
LEVEL OF INFORMATION 21
ESTIMATION OF RESERVES 23
SOME CLASSICAL RESOURCE ESTIMATION TECHNIQUES 23
Polygonal Methods 23
'Sectional' Methods 24
Triangular Methods 26
Inverse Distance Weighting (IDW) Methods 26
KRIGING 28
SYSTEMATIC RESOURCE ESTIMATION PRACTICE 28
FORMALISE ESTIMATION PROCEDURES 28
ALLOCATE RESPONSIBILITIES 29
DOCUMENT DECISION MAKING STEPS CAREFULLY 29
GEOLOGICAL MODELS 30
UPDATE AND REVISE ESTIMATION MODELS 30
BLACK BOX APPROACHES 31
A FINAL WARNING 31
3: STATISTICS 33
GEOSTATISTICS AND STATISTICS 33
SOME PRELIMINARY DEFINITIONS 34
UNIVERSE 34
POPULATION 34
SAMPLING UNIT 34
SUPPORT 34
2

NOTIONS OF PROBABILITY 35
EVENTS 35
PROBABILITY 35
MULTIPLICATION RULE AND INDEPENDENCE 35
CONDITIONAL PROBABILITY 36
RANDOM VARIABLES AND DISTRIBUTIONS 37
RANDOM VARIABLES 37
THE CUMULATIVE DISTRIBUTION FUNCTION 37
THE HISTOGRAM 39
How many Classes? 39
MOMENTS AND EXPECTED VALUE 40
EXPECTED VALUE 40
MOMENTS 40
The Mean (and the Median) 41
The Variance 42
Properties of the Variance 43
Measuring Dispersion 43
Standard Deviation 43
Coefficient of Variation 44
Other Moments 44
Skewness 44
Kurtosis 45
THE BOX PLOT 46
COVARIANCE AND CORRELATION 46
LINEAR REGRESSION 47
STATISTICAL TESTS 49
T-TESTS 51
MANN-WHITNEY TEST 51
WILCOXON MATCHED PAIRS TEST 51
COMMON DISTRIBUTIONS 51
GAUSSIAN (NORMAL) DISTRIBUTION 51
LOGNORMAL DISTRIBUTION 52
DEFINITION 52
Testing for Lognormality/Normality 53
probability plotting 53
Q-Q Plot 53
Chi-square goodness of fit test 54
Three Parameter Lognormal Distribution 54
Sichel's t-estimator 55
4: SAMPLING 56
WHAT IS THE OBJECTIVE OF SAMPLING? 56
EQUIPROBABLE SAMPLING 57
A SIMPLE STATEMENT OF THE PROBLEM 57
TYPES OF SAMPLING IN OPEN PIT GRADE CONTROL 58
TESTING DIFFERENT APPROACHES TO SAMPLING 59
BLAST HOLES (BH) 59
General Characteristics of BH Samples 60
Approaches to BH Sampling 61
Other Considerations 62
REVERSE CIRCULATION DRILLING 62
General Characteristics of RC Samples 63
Approaches to Sampling RC 64
Automation of Sampling 64
Rules of a Good Riffle Splitter 65
DITCH WITCH SAMPLING 66
CHANNEL SAMPLING FOR OPEN PIT MINING 66
UNDERGROUND GRADE CONTROL SAMPLING 67
FACE SAMPLING 68
DRILLING METHODS 68
OTHER CONSIDERATIONS 68
The Role of Geostatistics 69
PRACTICAL INTRODUCTION TO SAMPLING THEORY 70
COMPONENTS OF THE TOTAL SAMPLING ERROR 70
GYS THEORY OF FUNDAMENTAL SAMPLING ERROR 71
A Simplification 73
MORE ABOUT THE LIBERATION FACTOR 73
FRANOIS-BONGARONS MODIFIED SAMPLING THEORY 74
EXPERIMENTAL CALIBRATION 76
3

PRACTICAL IMPLEMENTATION 77
Sample Nomograms 77
EXAMPLE CALCULATIONS FOR A SAMPLING PROTOCOL 79
SAMPLING PRACTICE FOR GRADE CONTROL 81
5: SPATIAL VARIATION 83
RANDOMNESS AND OREBODIES 83
DETERMINISTIC APPROACHES 83
Trend Surfaces 84
PROBABILISTIC MODELS 85
RANDOMNESS 86
Coins and Dice 87
THE GEOSTATISTICAL APPROACH 87
THE DUAL ASPECTS OF REGIONALISED VARIABLES 88
REGIONALISED VARIABLES: CONCEPTUAL BACKGROUND 88
RANDOM FUNCTIONS 88
STATIONARITY 90
STRICT STATIONARITY 90
WEAK OR 2ND ORDER STATIONARITY 90
THE INTRINSIC HYPOTHESIS 90
THE STATIONARITY DECISION 91
THE VARIOGRAM 92
DEFINITION OF THE VARIOGRAM 92
MAIN FEATURES OF THE VARIOGRAM 93
Range and Zone of Influence 93
Behaviour Near the Origin 95
Highly Continuous Behaviour (Extreme continuity) 96
Moderately Continuous Behaviour 96
Discontinuous Behaviour 96
RandomBehaviour 97
ANISOTROPY 97
Geometric Anisotropy 97
Zonal Anisotropy 98
PRESENCE OF A DRIFT 99
PROPORTIONAL EFFECT 101
NESTED STRUCTURES 101
HOLE EFFECT 102
PERIODICITY 103
6: VARIOGRAPHY 104
THE SCIENCE AND ART OF VARIOGRAPHY 104
THE AIMS OF STRUCTURAL ANALYSIS 104
PRACTICAL ASPECTS OF A STRUCTURAL ANALYSIS 105
Preliminary Steps 105
Data Validation 105
Getting a Feel for the Data 105
Classical Statistics 107
HOW TO COMPUTE A VARIOGRAM 109
1-D: ALONG A LINE 109
2-D: IN A PLANE 110
3-D 111
ADDITIVITY 112
AN EXAMPLE 112
MODELS FOR VARIOGRAMS 114
NOT ANY MODEL WILL DO! 114
Admissible Linear Combinations 114
FROM A PRACTICAL VIEWPOINT 115
SOME COMMON MODELS 115
THE SPHERICAL MODEL 116
POWER MODEL 117
EXPONENTIAL MODEL 118
GAUSSIAN MODEL 118
CUBIC MODEL 119
MODELS FOR NUGGET EFFECT 120
APPARENT VS. REAL NUGGET EFFECT 121
Integration of Microstructures 121
4

Isotropy and the Nugget Effect 122
Sampling Error and the Nugget Effect 123
Locational Error 123
COMBINING MODELS 123
ANISOTROPIC MODELS 124
GEOMETRIC ANISOTROPY 125
An Example 126
ZONAL ANISOTROPY 127
WHY NOT AUTOMATED FITTING? 128
SYSTEMATIC VARIOGRAM INTERPRETATION 128
TEN KEY STEPS WHEN LOOKING AT A VARIOGRAM 128
1. The number of pairs for each lag in the experimental variogram. 129
2. Smoothness of the experimental variogram 129
3. Shape near the origin 131
4. Discontinuity at the originnugget effect 131
5. Is there a sill?transitional phenomena 131
6. Assess the range 132
7. Can we see a drift? 132
8. Hole effect 133
9. Nested models 133
10. Anisotropy 133
UNCOOPERATIVE OR TROUBLESOME VARIOGRAMS 134
CALCULATION OF THE EXPERIMENTAL VARIOGRAM 134
Theoretical Reasons 134
Definition of Stationary 134
Geographically Distinct Populations 134
Intermixed Populations 135
HOW TO DETERMINE APPROPRIATE VARIOGRAM CALCULATION PARAMETERS 135
Lag Selection. 135
Tolerances 135
Missing Values 135
EXTREME VALUES 136
OTHER APPROACHES TO CALCULATING VARIOGRAMS 136
ALTERNATIVE ESTIMATORS OF THE VARIOGRAM 136
ROBUST ESTIMATORS 136
RELATIVE VARIOGRAMS 137
Local Relative Variogram 137
General Relative Variogram 138
Pair-wise Relative Variogram 138
Sigma
2
i-j Relative Variogram 138
Some General Comments About Relative Variograms 139
VARIOGRAPHY OF TRANSFORMS 139
Logarithmic Transformation 140
Gaussian Transform 141
Indicator Transforms 142
A CASE STUDY OF VARIOGRAPHY 142
THE DATA 143
Advantages of Consistent Spacing 143
Histogram 144
Proportional Effect 145
VARIOGRAMS 146
Possible Non-Stationarity? 147
RELATIVE VARIOGRAMS 147
Pair-Wise Relative Variogram 147
Variograms of the Logarithmic Transform 148
EXTREME VALUES & VARIOGRAPHY 149
The Implications of the Transform 149
THE MODEL FITTED 150
Log Variograms and Relative Variograms 150
The Relative Nugget Effect and Non-Linear Transformations 151
Ranges 151
ANISOTROPY 151
Again: Possible Non-Stationarity? 152
VARIOGRAMS OF THE INDICATOR TRANSFORM 152
Why Use Indicators? 152
Selecting the Cut Off 153
Short Range Structures 154
SUMMARY OF VARIOGRAPHY 155
Variograms 155
Relative Variograms 155
Log Variograms 155
5

Indicator Variograms 155
CHARACTERISATION OF SPATIAL GRADE DISTRIBUTION 155
GEOLOGICAL FACTORS 156
Comparison of Geology and Variography 156
SUPPORT 157
WHAT IS SUPPORT? 157
"DISPERSION" AS A FUNCTION OF SUPPORT 158
SUPPORT EFFECT 158
An Example 158
HOW GEOSTATISTICS CAN HELP 163
THE IMPACT FOR MINING APPLICATIONS 163
VARIANCES OF DISPERSION WITHIN A VOLUME V 164
VARIANCE OF A POINT WITHIN V 164
VARIANCE OF V WITHIN V 164
KRIGE'S RELATIONSHIP 165
CHANGE OF SUPPORTREGULARISATION 166
REGULARISATION OF THE VARIOGRAM 166
RETURNING TO OUR EXAMPLE 167
8: ESTIMATION ERROR 170
WHAT IS EXTENSION VARIANCE? 170
EXTENSION VARIANCE AND ESTIMATION VARIANCE 171
THE FORMULA FOR EXTENSION VARIANCE 171
Factors Affecting the Extension Variance 173
OTHER PROPERTIES OF EXTENSION VARIANCE 174
EXTENSION VARIANCE & DISPERSION VARIANCE 174
PRACTICALITIES 176
Combination of Elementary Extension Variances 176
An Important Assumption 176
Geometry of Mineralisation 177
SAMPLING PATTERNS 178
RANDOM PATTERN 178
RANDOM STRATIFIED GRID (RSG) 179
REGULAR GRID 179
9: KRIGING 182
THE PROBLEM OF RESOURCE ESTIMATION 182
WHAT DO WE WANT FROM AN ESTIMATOR? 183
WHY KRIGING? 184
BLUEBEST LINEAR UNBIASED ESTIMATOR 184
HOW KRIGING WORKS 185
KRIGING MADE SIMPLE? 186
THE ADVANTAGES OF A PROBABILISTIC FRAMEWORK 187
KRIGING EQUATIONS 188
Choosing the Best Weights 188
The Unbiased Condition 189
Minimising The Error Variance 190
TERMS IN THE KRIGING EQUATIONS 190
The Lagrange Parameter 191
PROPERTIES OF KRIGING 194
EXACT INTERPOLATION 194
UNIQUE SOLUTION 195
KRIGING SYSTEMS DO NOT DEPEND ON THE DATA VALUES 195
COMBINING KRIGING ESTIMATES 195
INFLUENCE OF THE NUGGET EFFECT ON KRIGING WEIGHTS 195
Screen Effect 195
The Case of Low Nugget Effect, High Continuity 196
The Case of High Nugget Effect, Low Continuity 196
SIMPLE KRIGING 196
KRIGING PRACTICE 196
KRIGING NEIGHBOURHOOD ANALYSIS 197
HOW TO LOOK AT THE RESULTS OF A KRIGING 198
6

Make maps of the estimates 198
Check the location of very high and very low estimates 199
Look carefully at estimates near the margins of the deposit. 199
Examine the estimates in the context of geology. 199
Look at the kriging variance in relation to sampling spacing. 199
Look at the regression slope in relation to sampling spacing. 199
Examine the estimates for poorly sampled or unsampled areas. 199
THE PRACTICE OF KRIGING IN OPERATING MINES 199
GRADE CONTROL 199
Why Kriging? 199
Geology First! 200
Sampling 200
The Variogramas a Tool 200
Block Estimation 200
KRIGING TECHNIQUE 201
UPPER CUTS 201
10: NON-LINEAR ESTIMATION 202
SOMETIMES, LINEAR ESTIMATION ISNT ENOUGH 202
WHAT IS A LINEAR INTERPOLATOR ? 203
THE GENERAL IDEA 203
THE EXAMPLE OF IDW 204
ORDINARY KRIGING 204
NON-LINEAR 204
NON-LINEAR INTERPOLATORS 205
LIMITATIONS OF LINEAR INTERPOLATORS 205
AVAILABLE METHODS 206
SUPPORT EFFECT 207
DEFINITION 207
THE NECESSITY FOR CHANGE OF SUPPORT 207
RECOVERABLE RESOURCES 208
A SUMMARY OF MAIN NON-LINEAR METHODS 208
INDICATORS 208
INDICATOR KRIGING 209
MULTIPLE INDICATOR KRIGING 209
MEDIAN INDICATOR KRIGING 210
PROBABILITY KRIGING 210
INDICATOR COKRIGING AND DISJ UNCTIVE KRIGING 211
RESIDUAL INDICATOR KRIGING 211
ISOFACTORIAL DISJ UNCTIVE KRIGING 212
UNIFORM CONDITIONING 213
LOGNORMAL KRIGING 213
MULTIGAUSSIAN KRIGING 213
CONCLUSIONS & RECOMMENDATIONS 214

7

1: Int roduct ion
Real knowledge is to know the extent of one's ignorance.
Confucius
I arrived at geostatistics like most practitioners through necessity. As an
exploration geologist, I had the task of estimating a resource on a newly discovered
gold deposit. I had a gut feeling that there were significant uncertainties involved,
but no matter how many variations of polygonal shapes I tried to construct it was
clear to me that I was grossly over-simplifying things. Worse still I could not make
a connection between the methods I was using and the geological character of the
grade distribution I was faced with.
Recognition of incompleteness of our knowledge of a deposit (thus recognition of
the uncertainly in the problem) is the primary motivation for geostatistics. With
geostatistical tools, we can incorporate uncertainty into our modelling approaches.
Although geostatistical tools are now available within many computer packages and
used widely in the mining industry, in my experience few practitioners feel truly
comfortable with these methods. The range of text books available are either overly
mathematical (fine for geostatisticians, but not so user-friendly for people at the
mine) or too simplified. Unfortunately, some of the best texts now available do not
deal extensively with geological and mining problems.
This manual evolved from a set of notes prepared for a short course in Applied
Mining Geostatistics, which has now been presented on about 150 occasions in 9
countries about 1,500 participants since 1994. These participants were mainly mine
geologists, exploration geologists and mining engineers who were interested in
gaining a sound conceptual background to enable application of geostatistical tools
to real problems in the mining industry. A sprinkling of surveyors, managers,
chemists, metallurgists, computer scientists and mathematicians has also attended.
But this course was always, from inception, specifically targeted at professional
geologists and mining engineers faced with the practicalities of resource estimation.
Because the course has been run many times there has been gradual change in the
manner and order of presentation. This needed to be reflected in the
accompanying course manual. In particular, materials on stationarity and estimation
Chapter
1
8

were revised and some topics (kriging neighbourhood analysis, introductory non-
linear materials) were added or greatly expanded.
Acknowledgement s
I'm very much indebted to all those who have attended this course to date.
Teaching always benefits from a critical audience.
This manual, in various incarnations, benefited from discussions with our
professional colleagues: Daniel Guibal, Henri Sanguinetti, Michael Humphreys,
Olivier Bertoli and Tony Wesson. Dominique Franois-Bongaron kindly reviewed
sections of the previous manual and his constructive comments have been put to
good use during this revision. Although modified, some sections and specific
examples still owe debts to previous courses authored by Daniel Guibal, Margaret
Armstrong and Pierre Delfiner.
Colleagues and teachers originally shaped my own understanding of geostatistics: in
particular, Peter Dowd, Alan Royle, Henri Sans, Pedro Carrasco, Olivier Bertoli
and most importantly, Daniel Guibal.
Finally, the many clients (geologists and engineers) who have worked together with
us to try and solve real problems, and thus motivated development of clear
explanations of geostatistical concepts.
Prerequisit es
Beyond basic numeracy and some mining and geological vocabulary, there were no
prerequisites for the short course. Concepts and skills are stressed.
I believe it is a fallacy that good application geostatistics requires the user to
memorise and understand reams of impenetrable formulae. However, it is
dangerous to estimate resources and reserves using any methodology without
understanding the underlying assumptions and mechanics of the technique.
Consequently, some mathematics is unavoidable, but there is nothing that should
unduly panic a science or engineering graduate.
A reference list is included at the end of these notes so that you can take your
interest in geostatistics further, if you wish.
John Vann
Fremantle, February 2007
C H 2 R E S O U R C E E S T I M A T I O N
9

2: Resource Est imat ion
Concept s
The difficulties raised by the estimation problem are not of a
mathematical nature. We encounter them at two extreme levels:
at the initial stage of conceptualisation, i.e. of model choice,
and at the final stage of practical application.
Georges Matheron Estimating and Choosing 1989
Decision Making and Resource Est imat ion
Estimating mineral resources from drill hole data is an activity that is fraught with
difficulty. Most classical statisticians would regard the data for any ore reserve
estimate as dangerously inadequate. This would often apply even in cases where the
geologist felt that the deposit had been over-drilled.
The data for resource estimation are always fragmentary in nature. We have
samples separated by distances that are very large in comparison to the sample
dimensions.
However, the information we have increases with time, as more samples are
collected and geological knowledge improves. During the life of a project, there are
generally several stages, each of which corresponds to a different level of
knowledge of the mineralisation. At the conclusion of each drilling campaign, three
decisions are possible:
1. Stop everything, if we consider that the mineralisation cannot be
mined economically under current conditions.
2. Mine the deposit immediately if we assess that this will be
profitable.
3. Begin a new phase of exploration if the deposit is still poorly known
after the previous phase, or if we consider the economics to be
marginal.
Chapter
2
10

Because mining investments are generally large, the economic consequences of
making this choice are very important. Therefore, it is crucial that we evaluate the
mineralisation and its potential very carefully. In particular, it is critical that we
make the most of all the existing information at any decision step.
Resource evaluation is therefore a process, not an event. Resources will
always be estimated sequentially, and in general with more information as
the project progresses.
Geostatistics provides a consistent conceptual framework for resource
evaluation that makes maximal use of available information.
It has already been mentioned that the amount of information available
increases with time. Even so, the amount of data employed for the final
resource estimation prior to commencement of mining still constitutes
extremely scarce information.
For example: a large base metal deposit is drilled on 100m x 100m centres by 38
mm (BQ) cores of which half is crushed for analysis. This is not an uncommon
spacing for a huge porphyry copper deposit, for example. The density of sampling,
expressed as a proportion of the total volume of the deposit, is around 1.5 x 10
-8
.
Even with 10m x 10m drilling, which constitutes a very close pattern and would be
rarely achieved prior to the grade control stage, the density would still be very low:
around1.5 x 10
-6
. This is less than one ton of sampling per million tones of the
deposit, and by any statistical standards is a very small sample (in fact a sample
representing only 0.0000015% of the deposit)!
The performance of this calculation (tonnes of sample vs. tonnes of mineralisation)
is recommended for any geologist of engineer dealing with a resource estimate!
Sampl e Qual i t y
The statistical problem of very small (volumetric) sampling is not the only one we
facewhat is the quality of our sampling?
The recovery might be poor in some places. Different drilling techniques deliver
samples of different quality. Handling of samples may affect data reliability.
Samples below the water table will be less reliable when using any percussion
drilling technique (including RC). Biases may occur in both sample splitting and
analyses. The aliquot for assay in invariably very much smaller than the core or
RC split, so the correct reduction of samples in the lab is a critical problem. All
these factors will degrade the representivity of a sample. The degree of degradation
can be dramatic.
For further details of sampling, refer to Dominique Franois-Bongarons papers
or to Pitard (1990).

An Ex ampl e
Just how much data did we
collect?
11

Geol ogy
It hardly needs to be said that quality geological information is vital. More than this,
it is essential that the model used in the resource assessment stage is based on the
best possible interpretation of the available data, both assays and qualitative
observation. The geological model needs to be geometrically consistent and to
adequately capture the key geometric factors that influence the distribution of
potentially economic grades.
In general, the more complex the geology is, the more important its role in
resource assessment will be. The geometry of the mineralisation is often the main
determining factor when estimating tonnage. Clear distinction needs to be made
between those factors of interest in developing genetic and exploration models and
those affecting the distribution of ore at a scale of interest to the mining engineer
or mine geologist.
Ot her Fact ors
The most important remaining factor is the mining method. There are a number of
aspects to the consideration of mining factors when estimating a mineral resource
or reserve. These have a critical impact upon estimation and they are considered
later in some detail.
Est imat i on at Different St ages of a Project
Figure 1.1 Clustering

Fi rst Eval uat i on (Reconnai ssance)
This is the initial stage of a potential mining project:
Information is essentially qualitative and geological.
Few or sometimes no samples.
Model s
A scientific model is judged
by how well it works as a
predictive tool, not by
aesthetics
Clustered
Un-Clustered
12

Any samples existing tend to be preferentially located, and therefore
clustered.
The issue of clustering deserves some discussion. Clustering of values in our data
set is an almost universal source of bias in resource data sets. Figure 1.1 illustrates
the contrast between a clustered and un-clustered pattern, in 2D. Note that the
clustering of samples in high grade areas of mineralisation is common. The impact
of clustering in most resource data sets is therefore to bias the mean grade high (i.e.
overstate the average grade).
Any evaluation of mineral resources at this stage will be necessarily unreliable. The
main objective is to see, on a comparative basis, whether further work is warranted.
Decisions will be made on geological and other specific technical qualitative
grounds. Local block estimation will be of very little help: this is essentially a first
geological appraisal. However, the variogram (which we will become very familiar
with during this course) can be an excellent diagnostic tool even at the earliest
stage.
Fi rst Syst emat i c Sampl i ng
Once we have located mineralisation, a systematic sampling of the zone of interest
is generally undertaken.
The aim is to get a first quantitative estimation of global in situ resources. This includes:
The best possible definition of the limits of the mineralisation (geometry).
Estimation of the global mean grade.
Estimation of the global in situ tonnage.
Both qualitative (geological) and quantitative (assay) data are employed. At this
global level, there is no problem of choosing an estimator: provided that the sampling is
truly systematic, there is no risk of estimation bias
1
.
Preci si on and Accuracy
Precision is a measure employed in traditional statistics to quantify the reproducibility
of an estimate (or observation). Precision is proportional to the variance of errors
(or, equivalently, to the standard deviation of the errors). As such, the conceptual
equivalent in resource estimation is the estimation variance which is discussed at
length in Chapter 8. It is possible to have a precise estimate that has a poor
accuracy: in such a case, the measurements are closely reproduced, but biased.
Accuracy measures how close, on average, an estimate is to reality. Accuracy can
thus be defined as a relative absence of bias.

1
This is not true, of course, if the data we employ are biased because of drilling, sampling or assaying
problems!
Ear l y est i mat i on
At very early stages block
modelling may be an
inappropriate tool
13

No estimation methodology can adequately counter biased sampling or assaying:
Garbage in Garbage out
Note that the precision of the estimate is an important consideration. It depends
upon:
The number & type of samples (i.e. the sampling grid geometry).
The regularity and continuity of the mineralisation (i.e. the variability of the in
situ grades).
It can be easily established from geostatistical theory that a geologist or engineer
who feels that a regular grid results in a more precise estimate is quite right, and we
will tackle this subject in more detail later on.
At the stage of estimation of resources with the first systematic data, there are thus
several important factors to consider.
Figure 1.2 Schematic recall of precision and accuracy concepts.
Sampl e Type
The type of sample is defined by the physical means used to obtain it - drilling vs.
channelling or drill core vs. percussion chips for example. The representivity of the
sample type is critically important. It is essential to consider the volume of the
samples, their geometry and orientation: in short what geostatisticians call the
support of the samples.
Precise &
Accurate
Imprecise & inaccurate
Precise & inaccurate
Imprecise &
Accurate
14

The concept of sample support is central to geostatistics. In fact, it represents one
of the most important contributions of geostatistical theory to practical resource
estimation. We will consider this topic in detail in Chapter 5.
Resource Cl assi fi cat i on
Resources are generally classified, and any classification system is in part
establishing a nomenclature relating to their precision. Categorisation nomenclature
varies between countries, although in the past few there has been some measure of
convergence between North American, British and Australasian systems. The
JORC
2
Code is widely regarded as a model. A classical distinction employed, for
example, is the familiar one between Measured, Indicated and Inferred resources.
The JORC definitions do not give guidance on several important factors that
influence mineral deposit estimation. The JORC definitions are very much framed
in terms of the amount of exploratory samplings and openings and a qualitative
assessment of continuity, rather than in terms of quantifiable continuity of
mineralisation grade. The subject of geostatistics addresses the problem of quantifying
grade continuity.
The continuity of mineralisation may be quite distinct from continuity of its
geometry (geological continuity). This is an important distinction: a quartz reef
may be clearly continuous from hole to hole at a drill spacing of 100m x 50m,
but the associated gold grades may be totally uncorrelatable. This distinction is
recognised in the 1999 edition of the JORC Code.
Recoverabl e Resources at t he Earl y St age
The selective mining unit (SMU) is the smallest mineable unit upon which ore-waste
selection can be made. The size of the SMU defines the selectivity of the mining
operation. Because ore recovery in an operational mine is a function of the size and
geometry of the SMU, it is important that estimation of recoverable resource takes
the intended SMU characteristics into account.
Geostatistics provides techniques that make it possible to make global estimation
of recoverable resources even at this early stage, for example, by the Discrete Gaussian
Model (see Vann and Sans, 1995). This is a technique to estimate the global
recoverable resource, and it can be applied as soon as we can reasonably define the
variogram, histogram and geometry of the mineralisation. However, at this early
stage, local recoverable resources, i.e. determining the proportion of SMU's selected as
oreat a specified cut off gradefor local panels
3
, is generally not feasible.
Because of this, more closely spaced infill drilling is generally required.

2
Joint Ore Reserves Committee of the AusIMM, AIG and MCA.
3
When discussing local versus global resources we are using terms that are in general use by
geostatisticians. Local resources estimate the grade of individual blocks or "panels" in the deposit. Global
resources, on the other hand, are estimated for the entire deposit, or quite large zones, even though, at
early stages, we may not always be able to locate them in space. For example we may estimate a single
grade/tonnageor make several estimates of grade and tonnage at different cut off gradesfor the
whole deposit.
The J ORC Code
The JORC code is not
designed to give guidance on
how to estimate rather it deals
with how to report.
15

Infi l l Sampl i ng
This is the stage where we have drilled the deposit more closely and therefore:
1. We have more samples so we have a better definition of the grade
histogram.
2. We can thus better define the spatial distribution of grade.
3. We usually have improved geological models and thus better definition
of global tonnage.
This stage of estimation is usually critical. It may be repeated several times, each
time obtaining more sampling, if required. We will use the output to make mine
designs and run technical and financial feasibility calculations. It is difficult to
estimate resources at this stage and the consequences of mistakes are high.
It is rare for a mineral deposit to be completely extracted as ore during a mining
operation for two main reasons:
1. Technical: these relate to accessibility of ore grade material.
2. Economic: we must generally define some material as ore and the
remainder to be waste. In other words, we make a selection of
material to be processed as ore and material to be directed to the waste
dumps.
Because we will only generally recover as ore a proportion of the in situ
mineralisation, we must define two corresponding types of estimation of resources:
In Situ resources: Characterisation of the rich and poor zones of the
deposit with no account of the selective mining method to be employed.
Recoverable resources: Characterisation of the resources as a function of
the selectivity of the mining method and economic criteria.
Local Est i mat i on of
In Si t u Resources
Unlike global estimation of in situ resources, for local estimation of in situ resources
determination of the particular type of estimator to be used is an important
decision.
Many different local estimators can be used, each providing estimates of blocks or
panels of ore that are built from the local sample information. We examine a few of
these in the next section.
An important characteristic of an estimate is that it should be unbiased. An
unbiased estimator does not cause systematic over or under estimation of
resources. We also want our estimator to make the "best" use of existing
16

information, and in this sense, we are seeking the "best" estimate. Of course, we
will have to give a precise meaning to "best" in such a context.
We use estimates of a mineral resource for economic assessments, so it seems
natural that we would require some characterisation of the quality of estimation.
Are some areas better estimated than others? Which zones need more drilling?
On which factors does the quality (or precision) of our estimate depend? Here are
some of the more important factors:
Firstly, it is intuitive that the regularity of the mineralisation is a critical
factor in the reliability or quality of our local resource estimates. Given the
same amount of sample information, a more continuous mineralisation will
allow better local estimation results than an erratic mineralisation.
Secondly, the sampling pattern used is an important factor.
If we consider the two sampling geometries shown in figures 1.3 and 1.4 it seems
sensible that the first case (figure 1.3) should allow a better (more precise) estimate
of the block than the second case. The sampling pattern (sometimes referred to as
the "sampling geometry") has a strong influence on the quality of local estimation.
17

We will better estimate a block by a single sample if that sample is within the block.
More particularly, the optimal position for a sample would logically be in the centre
of the block to be estimated (and this is borne out by geostatistical theory, as we
will see later). Furthermore, it is intuitive that an even spread of samples around
the block will lead to better estimation than a situation where all available data is
clustered (see figure 1.4).

Figure 1.3 Two possible sampling geometries

Figure 1.4 Two more possible sampling geometries
Finally, the geometry of the block or panel to be estimated plays a role in
the estimation quality. This includes the relative dimensions of the block
with respect to the sample spacing.
If we take into account the above factors it is possible to assess the quality of any
estimator and thus select the one that will best meet our quality criteria.
Est imat i on of Recoverabl e Resources
To follow the JORC guidelines, here we use the term recoverable resources in
preference to the more usual geostatistical usage recoverable reserves because the
former term has no implication of economic or technical feasibility. To date, the
18

JORC code does not explicitly deal with the concept of recoverability (in the sense
used by geostatisticians).
The recoverable resources are, as stated earlier, a function of the selective mining
unit (SMU) we employ. Recoverable resources are also affected by the cut off grade
we assume and other technical parameters (e.g. minimum mining width). In an
open pit situation there are clear technical constraints in the sense that before we
can extract a given block as ore, we must mine all the blocks above it. There are
many factors involved in determining the recoverability of resources, but the most
important two, as far as resource estimation are concerned, are introduced below:
1. The support of the selection units.
2. The level of information.
" Support " of t he Sel ect i on Uni t s
Support is a term used by geostatisticians to describe the size, geometry and
orientation of the selection unit. The smaller the selection unit, the better able we
are to discriminate ore from waste, but the higher our mining costs will be. Figure
1.5 shows the influence of the selection support on the histogram of grades. Note
that V represents a larger support than v. For example, V could be a 10m x 10m x
10m SMU and v could be a smaller block, say 5m x 5m x 5m.
Figure 1.5 The influence of Support
There are several important things to note about the two histograms shown in
figure 1.5
The global mean m for both distributions is the same. The mean grade of
large blocks and small blocks are identical.
The histogram of the smaller support is more dispersed, i.e. it is more spread
out along the X-axis (which measures grade). This means there are more
Suppor t Ef f ec t
Support effect is a term
used by geostatisticians to
describe influence of support
on the statistics of samples
or other volumes.
19

high grades and more low grades measured on smaller supports in
comparison to large supports. The dispersion is measured by variance,
denoted
2
in the illustration. This is hardly surprising, because larger
supports represent groups of smaller supports, and thus averaging of smaller
supports. Extreme grades therefore tend to be smoothed out when we
consider larger supports. We expect a higher proportion of the samples to
have intermediate grades, when considering larger support.
If we apply the same cut off grade (zc) to both histograms, and if this cut
off is above the mean, then there is more metal above cut off for the
smaller support. Note that the proportion is the area under the curve.
Again, this makes intuitive sense, because using smaller support allows us
to avoid diluting the higher grade material with unavoidable lower grade
material. This is directly related to the concept of "selectivity"selecting
smaller mining units (SMU's) results in us extracting a higher proportion of
the in situ metal.
However, if we apply a cut off (zc) that is less than the mean to both
histograms, the situation is reversed: on samples we define more waste
than exists on block support.
The physical significance of support is completely familiar to any geologist who has
composited drill hole data, for example taking a file of 1m samples and producing a
file of 2m composites. The following example shows the impact of such a
compositing (often referred to as regularisation by geostatisticians) on statistics.
20

Table 1.1 1m sample set and corresponding 2m composites

Figure 1.6 Smoothing impact of compositing
AU (1M) AU (2M)
3.40 2.75
2.10
2.00 1.50
1.00
1.30 1.60
1.90
12.20 7.95
3.70
5.10 3.70
2.30
3.20 2.65
2.10
3.00 2.50
2.00
6.00 3.55
1.10
mean 3.28 3.28
variance 7.56 4.19
std dev 2.75 2.05
min 1.00 1.50
max 12.20 7.95
range 11.20 6.45
0 5 10 15
1
3
5
7
9
11
13
15
AU (1M)
AU (2M)
21

Level of Informat ion
Most mines employ sampling information from production blast holesor other
specific close-spaced grade control drilling/samplingto allow ore-waste
classification. The intention of selective mining is to truck to the mill only those
blocks that have average grade greater than a cut off (ore) and regard the remaining
blocks as waste. However, because the grades upon which we base this selection
are estimates, they are subject to smoothing and errorit is unavoidable that some
misclassification will occur, i.e.
we will send some waste blocks to the mill (because their estimated grades
indicate that they are ore), and
we will send some ore blocks to the waste dumps (because their estimated
grades indicate that they are waste).
Both of these misclassifications decrease the mean grade of the recovered ore and
thus reduce the profit of the operation. No matter how closely we grade control
sample, our information level cannot be perfect and thus misclassification is
unavoidable. Sending ore to waste and waste to the mill is unavoidable because we
make allocation decisions on the basis of estimates not reality.
It is therefore important that any strategy for selective mining aims at optimal ore
recovery, in the sense that it should minimise the amount of misclassification of ore
and waste.
The information effect refers to the relationship between the amount and spacing of
sampling available at the time of ore-waste classification and the number and
magnitude of misclassification errors when making ore-waste allocation.
The information effect concerns our lack of information at the time when we must
discriminate between ore and waste blocks. We will only have estimates for the block
grades instead of the real or "true" grades. It should be clearly understood that
estimates are always smoothed relative to reality. If we could select on the basis of true
grades we would make no allocation errors: we would correctly classify each block.
In essence, the problem is that we select on the basis of smoothed estimates, but
we feed the mill with the true (unsmoothed) grades.
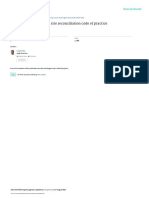
We can illustrate the information effect using a scatter diagram of true grades (Y-
axis) and estimated grades (X-axis) as shown in figure 1.7. Ideally, each block
estimate will be equal to the corresponding true grade, and all the points will plot
on the line Y=X. Because of the information effect, in practice, this is never the
case, and the points will plot as a "cloud", represented here as an ellipse. The area
of the plot can be divided into four quadrants depending upon the classification (or
misclassification) of blocks as ore or waste:
I nf or mat i on Ef f ec t
The information effect
concerns our lack of
information at the time when
we must discriminate
between ore and waste
blocks.
22

(I). The true grade of the block is above cut off, but we estimate the grade to
be below cut off. We therefore send ore to the waste dump.
(II). The true grade is above cut off, and we estimate the grade to be above cut
off. In this case we correctly classify the block and send profitable ore to
the mill.
(III). The true grade is below cut off, but we estimate the grade to be above cut
off. We therefore send unpayable waste to our mill.
(IV). The true grade is below cut off, and we estimate the grade to be below cut
off. We thus correctly allocate these blocks to the waste dump.
Figure 1.7 Information effect (see discussion intext)
Clearly we wish to minimise I and III and maximise II and IV. It also follows that
we wish to have an estimator that results in a scatter plot with the long-axis of the
ellipse at approximately 45 This is because any deviation from this will result in
increasing conditional bias. We also want to make this ellipse as "thin" as possible to
reduce the number of allocation errors. However, it is important to understand that
this ellipse cannot ever thin-out to a line (i.e. Y=X) because for this to happen we
would need to know the exact true grade of every location in the mineralisation!
The issue of conditional bias is also seen in figure 1.7. This figure shows a case
where the estimate is globally unbiased (i.e. the mean of the estimates is equal to
the mean of the true grades). The expected true grade of blocks that have a given
estimated grade can be plotted for a range of estimated grades. If we draw a curve
through the resulting points, we obtain the conditional expectation shown on figure
1.7.
Condi t i onal Bi as
Lack of perfect or
exhaustive information
implies that correlation
between estimates and true
block grades will be
imperfect. This in turn
implies overstatement of
high grade and
understatement of low
grades, on average.
23

In reality, we never know the true grades of blocks: the ultimate information we
have are our smoothed estimates. Therefore, we want our estimates to be as
conditionally unbiased as possible, in other words, we wish the conditional
expectation curve in figure 1.7 to deviate as little as possible from the 45 bisector.
However, the regression line Z
v
|Z
*
v
will never be 45 if there is any degree of
scatter in the plot.
We will note below that polygonal estimators are always highly conditionally biased.
Est imat ion of Reserves
Resources that are estimated with a "sufficient" degree of confidence (and the
JORC code loosely defines this in terms of sampling density and types of sampling)
may be classified as reserves if, and only if:
A study of technical and economic feasibility (including mine planning and
processing feasibility) has been completed, and
The reserve is stated in terms of mineable tonnage and grade.
Clearly the second factor (and, in part, the technical requirement of the first factor)
imply that a recoverable resource be estimated as the basis for an ore reserve.
Recoverable reserves account for the support effect in addition to other technical
factors (dilution, mining methods, constraints) and any economic considerations.
Some Cl assi cal Resource Est imat i on Techni ques
A common characteristic of all the methods considered below is that these
estimators are all linear combinations of the data.
Pol ygonal Met hods
Polygonal methods have the longest history of usage for mining estimation
problems. Each sample is located at the centre of a polygon defined by the
bisectors of segments determined by sample pairs (see figure 1.8). The mean grade
of each polygon is estimated by the grade of the central sample.
This estimator has the advantage of being quite simple to build manually. In
addition, given a sampling pattern that is not clustered, the polygonal method will
result in an unbiased estimate of the global resources.
However, as far as local estimation is concerned, the polygonal method is very
poor, because:
1. It does not take into account the spatial correlation of the mineralisation.
24

2. It does not use any data other than the centrally located sample.
3. It generally results in severe conditional bias.
Figure 1.8 The idea of polygonal estimation
In particular, it should be noted that polygonal estimators are heavily conditionally
biased when used to estimate recoverable resources, as a matter of fact the
histogram of the estimates is identical to that of the samples. The support effect may
have quite a marked impact on the grade above a given cut off, but it is not
accounted for at all. This is one of the reasons that most polygonal estimates
(especially for gold) often require heavy cutting of sample grades.
' Sect i onal ' Met hods
This type of estimator should only be used for global resources, although they are
sometimes (inadvisably) reported section by section. Figure 1.9 illustrates the basic
methodology. Sectional methods represent a variation on the idea of polygonal
estimation.
Pol ygonal Met hod
This method is inadvisable
for most practical mining
situations because it
effectively maximises
conditional bias.
25

Figure 1.9 Sectional method

The mean grade g
i
of the drill samples in intersections of mineralisation are
weighted by their intersection thickness t
i
and assigned to an area defined on
section. This area A is measured (traditionally with a planimeter, these days by a
computer program).
The grade of the section is calculated by the weighted average:
z
g t
t
i
i
N
i
i
i
N
*
=

=
=
1
1

The area of the mineralisation on this section is then projected half way to the next
section to obtain a mineralisation volume. Using a manual technique this volume
may be derived by simple orthogonal projection. Using computerised methods,
some more sophisticated means (wireframing) may define the volume.
This method suffers from most of the problems inherent in the polygonal method
described above and is only applicable for global estimation of in situ resources for
the same reasons. Local estimation is not really possible, even at the level of
sections. In particular, no account of support or spatial correlation can be made in
a local sense.
Sec t i onal Met hod
Each section is treated
independently in this
method. Would you do that
when interpreting the
geology?
26

Tri angul ar Met hods
These methods, rarely if ever used today, were the ancestors of inverse distance
weighting. There are (or were) two variants:
1. The mean grade of a triangle defined by the three corner samples is
estimated by the average of these three grades. When used for
estimation of local in situ resources, this method has the same
drawbacks as the previous one.
2. A second approach is to estimate small blocks. Any block within the
triangle is estimated by a linear combination of the corner holes. The
weights used are often inversely proportional to the distance of the
sample to the block. Again, this method (although easily computerised)
does not take into account important factors influencing the
estimation.
Inverse Di st ance Wei ght i ng (IDW) Met hods
Inverse distance weighting methods are more modern than the preceding
techniques, and became quite widespread with the introduction of computers. The
mineralisation to be estimated is divided into blocks, generally of equal size. The
mean grade of a block is estimated by a weighted linear combination of nearby
samples (see figure 1.10).

Figure 1.10 The idea of interpolation

The weighting factors give greater weight to closer samples, using the formula:
27

i
i
i
i
N
d
d
=
=
1
1
2
2
1

where d
i
represents the distance of sample i to the centre of the block being
estimated. Only samples within a given "zone of influence" are utilised in the
estimation. The method can take into account the spatial correlation of grades,
albeit in a rough manner, if it is implemented using powers other than two, i.e.
i
i
i
i
N
d
d
=
=
1
1
1

where is any chosen power. For example, to reduce the weight given to more
distant samples we may choose = 3 or more.
The IDW method is a generalisation of the triangular method (the 2nd variant we
discussed) and is easily computerised. Most mine planning software can implement
IDW. Although it is a decided improvement upon polygonal methods, it still does
not account for the known correlations between grades. The method relies on an
arbitrary model for the spatial structure of mineralisation. In particular, the reasons
for choosing any particular power are not clear. The choice may be:
Intuitive often a very poor choice, especially if the stated aim is to
reduce the influence of grades in a situation of poor grade continuity.
Against production data.
By cross-validation, or
By comparing results to a better estimator (e.g. kriging).
The "classical" methods do not rely upon the spatial structure of the data: this is
their main drawback.
Implementations of IDW can be made that incorporate anisotropy. Calculation of
variograms is often made to determine the ratios of anisotropy. In such a case most
of the work has been done towards a geostatistical estimate, however the IDW
estimator (even with anisotropy accounted for) does not correctly model the
distribution of grade. We will discuss this in more detail during the course.
A further problem with IDW is that samples at the centroid of a block have a
distance of zero, leading to mathematical failure of the method unless some ad hoc
translation of data is used. In any case, samples near the centroid tend to get most
of the weight (regardless of the power used).
I DW Met hod
A big step forward from
polygonal approaches, but
not without pit-falls.
28

Note that classical or traditional methods may be "fine tuned" once we are mining.
However, there is no way to get "optimal" estimates from these techniques prior to
exploitation.
Kriging
In the early 1960's, Georges Matheron of the Paris School of Mines (Matheron,
1962, 1963a, 1963b) developed a general solution to the problem of local
estimation that built upon an empirical solution developed by the South African
mining engineer D.G. Krige. To honour Krige's pioneering contribution in this
field (Krige, 1951) , Matheron named the new technique he developed kriging.
Kriging is a way of assigning the weights
i
such that they reflect the spatial
variability of the grades themselves. This estimator will also weight a sample
according to its position relative to the block we are estimating. Furthermore,
kriging assigns the weights in a way that can be shown to be mathematically
optimal. Finally, kriging allows us to state the average error incurred in estimating a
panel of defined geometry in a given deposit, using a particular arrangements of
samples.
Kriging is a statistical method, i.e. it is built upon the ideas of probability theory. In
fact, kriging is a type of distance-weighted estimator where the distance employed
is a measure spatial correlation (variogram distance) rather than conventional
(Euclidean) distance.
We will now quickly recall some basic statistics and probability, followed by an
introduction to the idea of regionalised variables. Then we will tackle the problem of
calculating and modelling variograms. After considering a few very practical (non-
estimation) uses of variograms, we will finally return to the technique of kriging.
Syst emat ic Resource Est imat ion Pract ice
Our aims in resource estimation do not end at "getting the best estimate" from a
statistical or numerical point of view, important though that aim is.
It is critical that we also formalise the estimation process, allocate responsibilities
clearly, document the estimation adequately and take the geology into proper
account.
Formal i se Est i mat i on Procedures
Making an estimate is a process, not an event. Estimation is a dynamic series of
steps and we may wish to repeat certain steps, or incorporate new observations. To
make the process of "revisiting" our estimates easier, formalisation is required. A
good resource estimate needs to be thoroughly documented so that it can be
repeated. Of course, a well-documented procedure also facilitates efficient resource
audit and easier transitions if project staff change.
Kr i gi ng
Kriging is mechanically
much like IDW. What
differs is the way that the
weights are derived. The kriging
weights are not arbitrary:
they are based on data
correlations.
Doc ument at i on
Quite apart from the
professionalism of
documenting the job, there
are other good practical and
legal reasons for competent
documentation.
29

The resource evaluation procedure starts with data collection, geological
interpretation and validation. From this early stage, the procedure used should be
documented and formalised:
Step Test/Control
Step 1 Collect samples Check representivity...
Step 2 Sample preparation Quality Control
Step 3 Assay Quality Control
Step 4 Hole survey Quality Control
etc...
For major resource delineation programs, standards, control procedures etc. should
be implemented and documented from the earliest stages of the project. A review
of quality control in geochemical sampling programs is given by Thompson (1984).
The best starting point for assessing sampling practices are Dominique Franois-
Bongarons papers.
Formalisation and documentation should be implemented for each step of the data
acquisition and resource estimation process.
Al l ocat e Responsi bi li t i es
At each step, responsibilities need to be clear: who sites holes? who monitors assay
quality control? etc.
Estimation begins with data collection, data validation and critical examination of
the geological model. If there are important mining constraints to be accounted for
early in this process, then a mining engineer must be brought on board early on.
Experience shows that team approaches are generally superior to lone efforts.
Several people, in particular if their specialisations are different, tend to create a
constructively critical environment that results in more objective decision making.
Document Deci si on Maki ng St eps Careful l y
Estimation of mineral resources involves many decision making steps. A geologist
or mining engineer revisiting the estimate should be easily able to answer such
questions as:
Which holes were used in the estimate?
If some holes were not used, why?
What are the justifications of the key features in the geological
interpretation? Why was this particular model used? Are there rational
alternatives?
30

If populations were split (e.g. oxide versus primary or northern end versus
southern end), why? If different lithologies were combined in the
estimate, why?
If different sampling techniques (e.g. RC and DDH) were treated in the
same way, how is this justified? If not, how were the differences quantified
and accounted for?
If repeat assays were available were these used, and if so, how?
If grades were cut, how and why?
If a particular estimation methodology was selected, why?, etc.
For each deposit the specifics will be different, but the general scheme will still
apply.
Geol ogi cal Model s
Note that all geological interpretations constitute models, whether this is explicit or
not. The type of model used in estimation will be most reliant, in general, on the
larger scale features that impact upon the spatial distribution of mineralisation.
Genetic geological models and exploration models will often be a superset of the
model required for resource estimation.
The critical features of the geological model used for resource estimation generally
relate to geometry: stratigraphic contacts, folding, location of faults and
discontinuities, identification of vein orientations etc. Knowledge of a genetic link
between assayed elements (Au and As for example, or Pb and Ag) may be a useful
part of the model.
We will see later that one of the most important (if not the most important)
decisions made in the estimation process is that of stationarity. We will rigorously
define stationarity in subsequent chapters, but for the moment we can summarise
the concept by: stationarity decisions involve sub-setting (or re-grouping) data such
that the resultant data sets may be legitimately employed for statistical analysis and
estimation. The geological model is a primary input to stationarity decision-
making, and may be also influenced by that decision-making.
The practical consequence is that we must build geological models for the purposes
of grade estimation by paying attention not only to the geology, but also to the
grade distribution.
Updat e and Revi se Est i mat i on Model s
As more sampling or geological information becomes available it is often necessary
to update and revise our estimation. At these times, it may be possible to improve
the estimation algorithm or the way in which we incorporate geological features
into our model. The potential financial advantages (i.e. increased profits) that may
result from optimal estimation can be significant. Staying with an estimation
procedure that is not performing well, or simply applying "mine-call" factors as a
Geol ogy
Lack of good geological
modelling is a detriment to
any estimate. However, good
geology is not enough, we
must also estimate sensibly
within geological
boundaries.
31

band-aid solution will probably cost the mine, i.e. result in lost profits. During the
life of a mine several estimation procedures are often used with the aim of constant
improvement.
Black Box Approaches
The whole point of formalisation, objectification and revisiting is to avoid so-called
"black box" approaches. A black box approach is one in which the assays are
shoved into a computerised (or for that matter, manual) effectively fully automatic
resource estimation procedure that no-one involved really understands. Classic
answers to the question why are you estimating this (or that) way? from people
using black box approaches include:
This is the way it was done for the feasibility study and we're locked in.
We have a policy from head office that this procedure be followed on all
deposits.
This is the only technique our software is set up to do.
The ore reserves system was set up by (insert name of long-departed
geologist/engineer) and we are unsure of how to go about changing
anything.
If assumptions are challenged and decisions understood all the way through the
process, a "black box" approach is not possible.
A Final Warning
The three biggest single causes of serious error in resource estimation, in our
experience, are:
Unchecked data. Monstrous errors can lurk in databases for years and they may
not be obvious. Frequently the authors have dealt with data that we assured is
checked, only to locate trivial and serious problems. Simple keying errors or
coordinate shifts can result in seriously erroneous estimations. The number one
priority when setting up a resource estimation procedure is to instigate rigorous
data checking and database quality systems. Different versions of the same
database also coexist at some mines. Database integrity policy is easily followed
once instituted.
Poor geological understanding or control. A poor geological model (i.e. one
which does not allow adequate characterisation of geometry) is an obvious example
of potential disaster. Again, it should be emphasised that the detail of the model
needs to be aimed at characterising the distribution of mineralisation at scales with
mining engineering significance. It is also clear that failing to utilise such a model
intelligently can cause serious trouble: we all know stories of ore blocks being
interpolated well beyond inferred mineralisation limits (or into mid air...).
Bl ac k -Box
Input data; have little or no
understanding of process;
get dubious or
uninterpretable results.
32

Critical errors in interpolation. For example, use of an interpolation that assumes
a high degree of spatial correlation when the data do not confirm this, or other
misspecification of the model for grade variability.

C H 3 S T A T I S T I C S
33

3: St at ist ics
Three statisticians go deer hunting with bows and arrows.
They spot a big buck and take aim. One shoots and his arrow
flies off ten feet to the left. The second shoots and his arrow goes
ten feet to the right. The third statistician jumps up and down
yelling, "We got him! We got him!
Bill Butz, quoted by Diana McLellan in Readers Digest, June 1995
Geost at ist ics and St at ist ics
Geostatistics is a branch of applied statistics
4
dealing with phenomena that fluctuate
in space (Olea, 1991). As such it is built upon a foundation of probability theory
and statistics. Consequently there is some unavoidable material that needs to be
appreciated before we get going on geostatistics per se.
One aim of this chapter is to provide a vocabulary of terms and an understanding
of some basic concepts of probability and statistics that are required later. This
chapter is also intended to refresh any statistics you have (which may be rusty) and
provide you with some useful tools to look at our data. The material is presented in
enough detail that this chapter will provide reminders of the basics of probability
and statistics for later revisions.

4
Noteyou may still see American authors defining geostatistics as "the application of statistical
methods to geological data", however, this definition is obsolete and the specific definition given here is
now universally accepted.
Chapter
3
C H 3 S T A T I S T I C S
34

Some Preliminary Definit ions
Universe
The universe is the entire mass or volume of material that we are interested in as a
source for our data (and all possible data). In mining geostatistics this is generally
the mineral deposit at hand, although it could be a zone (or some other subset) of a
mineral deposit or even a group of deposits. It could also be a stratigraphic
horizon, an exploration lease, etc. As such it may have clear, sharply defined
boundaries or be imprecise (the margins of a poorly known body of mineralisation,
for example).
Popul at i on
The population is the set of all possible elements we can obtain from a defined
universe. As such, the definition of a given population is closely linked to the
specification of the sampling unit. For example, if our universe is a particular gold
deposit, then the following populations might be of interest:
The set: all the possible 1m RC samples in the deposit.
The set all the possible 25m x 10m x 5m resource panels in the deposit.
The set all the possible 5m x 5m x 5m selective mining units in the
deposit.
So, we can define many populations from a given universe. It is important to
clearly define both the universe and the population we are considering in any
statistical or geostatistical study. Although this may seem quite obvious, it is not
uncommon to see reports in which vague references to the samples are made,
without such a definition.
Sampl i ng Uni t
Each individual measurement or observation of a given population is a sampling
unit. For example: 1/2 core samples, 1/4 core samples, RC grab samples, RC split
samples, blast hole samples, etc. Again, it is essential to carefully define and
document this. Especially as the precision with which the resulting sample
represents the sampled material is directly linked to this definition (see next
section).
Support
A fundamental concept in geostatistics, introduced in the previous chapter, is that
of support. The support of a sample is defined by its size, shape and orientation.
Unlike classical statistics, where there is a natural sampling unit (a person, a tree, a
light bulb...) there are many possible sample supports in problems involving
sampling for chemical assay, etc. The support is thus very important, because some
statistics (especially the variance) are closely linked to the support selected.
Examples of support definition are:
Suppor t
Unlike classical statistics,
where there is a natural
sampling unit there are
many possible sample
supports in geostatistical
(spatial) problems.
35

A vertical 1.5 m long 1/2 HQ triple tube core sample.
A vertical 2 m long 1/2 HQ triple tube core sample.
A 2 m long, 5 kg horizontal channel sample across a face.
An 8-pipe 10kg sample taken from blast hole (BH) cuttings.
A 5m x 5m x 3m grade control-scale mining block.
A 25m x 25m x 10m resource estimation-scale block.
Not ions of Probabilit y
While there is a voluminous literature on the probability theory, only a small
portion of which is necessary to practical geostatistics. A good introduction to
statistical and probabilistic concepts might be gained from Davis (1986).
A few basic notions are required for this course, and probably useful in mining
applications generally, and we summarise them here.
Event s
An event is a collection of sample points that defines an outcome to which we
might assign a probability. Events may be transformed or combined, and can be
viewed as sets. The notation and algebra of sets is thus commonly employed in
probability theory.
Probabil i t y
To every event A we may assign some number Pr(A) called the probability of the
event A. Probabilities are measures of the likelihood of propositions or events. For
example, the event may be the average grade of the material in a given stockpile is
greater than 1.5 g/t Au. The scale for probabilities ranges from 0 (the event is
impossible) to 1 (the event is a certainty), i.e.
0 1 Pr( ) A
Because Pr( ) = 1 and Pr( ) = 0 it follows that the probability of the
compliment of an event, i.e. that the event does not occur, is:
Pr( ) Pr( ) A A = 1
Mul t i pl i cat i on Rul e and Independence
A fundamental notion in probability is that of independence. Two events A and B are
independent if the probability that both A and B occur is the product of their
respective probabilities, i.e.
36

Pr( ) Pr( ) Pr( ) , A B A B A B = independent

The event both A and B occur is called a compound event and is also denoted:
Pr( ) Pr( ) Pr( ) Pr( ) AB A B A B = =
The way in which we calculate probabilities of compound events is defined by
whether or not the events can be considered as independent or dependent.
The classic example is the successive tossing of a coin: we flip a fair coin twice and
the probability of the outcome Heads, Heads is:
Pr( ) Pr( ) Heads Heads
= =
1
2
1
2
1
4

The intuitive idea of independence of two events A and B is that knowing A has
occurred conveys no information about the event B. It is often assumed in
statistics, for example, that the measurement of errors is independent.
Condi t i onal Probabi l i t y
If A and B are two events, the probability that B occurs given that A has already
occurred is denoted:
( ) Pr | B A
and is called the conditional probability of B given A. The notion of conditional
probability is closely linked to that of independence. If the occurrence or non
occurrence of A does not help us to make statements about B then, as we have
already said, we can state that A and B are independent events. In this case we can
evaluate the conditional probability very easily:
( )
( ) Pr | Pr , B A B A B = for independent
If the occurrence or non occurrence of A does help us to make statements about B
then we say that A and B are dependent events. In this case we may still be able to
assign a numerical value to the conditional probability. Conditional probability has
an important role in resource estimation statistics and geostatistics.
Examples of conditional probability in mining applications might relate to cut off
grades. For example:
The probability that the estimation error for a mining block is 1% (B)
given that we consider a block that has an estimated grade greater than 2.5%
Cu (A).
37

The probability that we select a block that has a true grade below 1.2 g/t
Au as ore (B) given that we select a block that has an estimated grade
greater than or equal to 1.2 g/t Au (A).
As we have just said, the way in which we calculate probabilities of compound
events is defined by whether or not the events can be considered as independent or
dependent. In particular:
Pr( ) Pr( )
Pr( ) Pr( ) ,
A B AB
A B A B
=
= for independent

and
Pr( ) Pr( )
Pr( ) Pr( | ) ,
A B AB
A B A A B
=
= for dependent

Random Variables and Dist ribut ions
The idea of a random variable is central to both statistics and geostatistics.
Random Vari abl es
A random variable (RV), which we usually denote by a capital letter X (etc.), is a
variable that takes on numerical values, usually denoted by lower case letters:
{ } x x x x
n 1 2 3
, , ,..., , , according to the outcome of an experiment to which we have
assigned relevant probabilities. More strictly, a random variable is a function whose
domain is a sample space and whose range is some set of real numbers.
For example, if the experiment is a toss of a coin we might assign the score 1 to the
outcome Heads and 0 to the outcome Tails. We then have a random variable X
that can assume the following values:
X =

1
0
with probability 1/ 2
with probability 1/ 2

So, a random variable is just a function that takes on certain numerical values with
given probabilities.
The RV X may take on values (also referred to as realisations) that are members of a
possible set of values { } x x x x
n 1 2 3
, , ,..., , . The word random in this usage does not
suggest that the numeric values that the RV takes on are distributed randomly. It is
implied that the RV assumes particular numeric values with a certain probability
and that this probability can be estimated from a frequency distribution
constructed from a sufficiently large random sample of outcomes.
The Cumul at i ve Dist ri but i on Funct i on
Any random variable X is defined by its cumulative distribution function:
Random Var i abl e
A random variable is a
function whose domain is a
sample space and whose
range is some set of real
numbers. Grades in a
deposit can be easily
conceived of as a random
variable.
38

( ) [ ] F x X x x = < < Pr
This is the probability that X is less than or equal to some value x. By construction,
the function F(x) is monotonically increasing from 0 to 1 (see figure 2.1a).

Figure 2.1 a: cumulative probability function and b: probability density function.

If we are interested in the probability that X lies in a given interval (a,b), we have:
Pr ( ) ( ) a X b F b F a < =
If the interval (a,b) is very small, lets say:
b a dx =
then the probability that X lies in the interval:
x
dx
x
dx
+
2 2
,
can be written as:
( ) Pr x
dx
X x
dx
F x
dx
F x
dx
F x dx < +
= +

2 2 2 2

Provided that X is a continuous function. You may recall from calculus that ( ) F x
is the derivative or slope of F(x) at x and we denote it f(x) (see figure 2.1b).
39

f(x) is the derivative of the cumulative distribution function and is referred to as the
density of probability at the point x. The function f(x) is called the probability density
function.
The area under the curve f(x) is the probability and it should be understood that the
value f(x) itself is not a probability (for instance, the value of f(x) may be greater
than 1). The relationship between f(x) and F(x) is shown in figures 2.1a and 2.1b.
F(x) is the area under the curve f(x) up to a certain point x, i.e.
( ) ( ) F x f x
x
=

The Hi st ogram
Figure 2.2 Histogram
The way to estimate f(x) from the data is to construct a histogram.
A histogram is built by dividing the range of values (i.e. the interval between the
largest and smallest observed data) into a number of classes. We then count the
number of observations in each class. The resulting value in each class is an integer
but these may be divided by the total number of data to produce a relative frequency
histogram.
How many Cl asses?
The next obvious question is: how many classes to use for our histogram? This is
an important consideration, because if the classes are too wide, information about
the density function we are estimating is lost due to smoothing of the histogram.
Alternatively, if we define classes that are too narrow, we may get very few (or no)
observations falling into each of them. This will result in an estimate of the
Hi st ogr am
A histogram is a
visualisation of a random
variable.

f
r
e
q
u
e
n
c
y

Grade (%)
40

histogram that is quite sensitive to the exact position of class boundaries and so the
variability of our density estimate will be too high.
A rule of thumb is not to define classes in such a way that fewer than five
observations fall within each. Some practitioners also use the rule of thumb that the
minimum number of classes is:
NClass N = 10
10
log ( )
If we have a large number of observations, we should not have difficulty in
defining the shape of the histogram fairly well. More than 20 classes are rarely
required for this unless the distribution is highly skewed, i.e. there are a few values
falling a long way from the majority of the data.
Moment s and Expect ed Value
This section is important, because the theoretical basis of geostatistics requires an
understanding of the following ideas.
Expect ed Val ue
The expected value or mathematical expectation E(X) of a random variable X is obtained
by finding the average value of the function over all possible values of the variable.
The symbol E denotes the operation of computing an expected value.
The expected value is thus an ideal or theoretical average. In fact it is the limit of the
sample average when the sample size increases indefinitely. As such the terms
expected value and mean are equivalent. Note that we do not necessarily expect
samples taken from a distribution to have an average value equal to the expected
value unless our sample is large.
Note that, in some cases the value of a given outcome of X (i.e. x) cannot possibly
take on the value of the expectation. For example, if we define Heads as 1 and
Tails as 0, for a fair coin the expected value is 0.5.
The operation of computing the expected value is linear, namely:
E c c
E cX cE X
E X Y E X E Y
=
=
+ =

+

where c is a constant and X and Y are random variables.
Moment s
The concept of the moment of a distribution is the basis of many summary
statistics used in geostatistical and other applications of probability theory. To
determine, or specify, the form of a particular probability distribution from
Ex pec t ed val ue
An ideal or theoretical
average.
41

experimental data requires the estimation of its parameter(s). Moments are useful as
summaries for such specification.
The concept of a moment will be familiar to you if you have studied physics, in
particular, mechanics. In this usage, the moment of a force can be defined as its
magnitude multiplied by the distance between its line of application and the axis of
rotation. So, forces applied at increasing distances from the axis of rotation have
greater rotational effectgreater moment.
In statistics, we are interested in the distribution of random variables, which are
numeric scores. We can define (statistical) moments about any selected axis i.e.
about any desired value of X. The kth moment of X is usually denoted
k
and is
defined as:
[ ]
=
=
k
k
k
E X
x f x dx ( )

The first moment is thus:
= =
= =
k
k
E X k
m E X
1
1

i.e. the first moment of a distribution is the mean m (or expectation).
The Mean (and t he Medi an)
Now, this makes sense intuitively, because the mean can be considered as the centre
of a distribution. More precisely, the expectation (the first moment) is the centre of
gravity of the distribution. For this reason, the mean is sometimes referred to as a
location parameter of the distribution.
Other measures of location or central tendency may be used rather than the mean. For
example, the median M, which is the value such that half the observations are
greater than M and half are less. The median, also sometimes denoted
~
m, is highly
robust (i.e. not strongly affected by extreme values). However, the mean has a
strong intuitive appeal when we are dealing with additive qualities, because
multiplication of the mean grade, for example, by the tonnage yields the metal. This
is not a property of the median.
More importantly, the mean is a measure of central tendency that minimises the
quadratic errors (i.e. error variance).
Another property of the expectation worth noting is that, if X and Y are
independent RV's:
E X Y E X E Y =
Moment s
Moments, including the
mean, variance, skewness
etc., are convenient
summaries of a distribution.
Conc ept
The mean is the centre of
gravity of a distribution.
Thats why it is easily
affected by extreme values in
the tail.
42

Now, we may also calculate moments about any given centre (or origin), but of
most interest to us in statistics are moments calculated about the arithmetic mean.
[ ] ( ) E X x f x dx
k
=

1 1
( )
In this manner, we may calculate the kth moment about the mean.
The Vari ance
Measures of central tendencies such as the mean and median are important in
summarising data and characterising distributions. We are also usually interested in
a measure of the spread or dispersion of the values. Again, there are a variety of
statistics we can employ, for example, the range (maximum value - minimum
value). However, a measure that is centred on the mean makes intuitive sense in
most cases.
We might calculate the mean deviation about the arithmetic mean, but there is a
difficulty. By definition, the mean is the first moment of the distribution (its centre of
gravity) and as such the sum of positive deviations is equal to the sum of negative
deviations, i.e. the average of all deviation from the mean is equal to zero. Not very
useful. So we might employ absolute values to overcome this:
X m
N
i
i
N
1

This measure (the mean absolute deviation or MAD) is not often used in statistics,
in part because absolute values present difficulties in calculus, but also because
there is a better theoretical measure of average deviation from the mean: the
variance.
The variance occupies a key position in both statistics and geostatistics. It is the
second moment about the mean, i.e.
[ ]
( )
[ ] [ ]
Var X E X m
x m f x dx
x f x dx m
E X E X
( )
( )
( )
= =
=
=
=
2
2
2
2 2
2
2

The annotation Var(X) and
2
are equivalent and they relate to the parameter
variance which is estimated by the statistic s
2
:
Var i anc e
A measure of dispersion (or
spread of values) about the
mean. This is the most
common measure of
dispersion used in
geostatistics.
43

( ) s
N
x m
N
x m
i
i
N
i
i
N
2
1
2
2
1
2
1
1
=
=

=
=

where m (the arithmetic mean) is estimated by the sample mean x .
You may also see the formulation of s
2
divided by (N-1) rather than N. This
compensates for bias when N is small, and has no importance for cases where N is
large.
Note that in mining geostatistics the notation D
2
is often used for variance (D for
dispersion).
Propert i es of t he Vari ance
The main properties of the variance are:
0

+ ar
Var c
Var X c Var X
Var cX c Var X
Var X Y Var X V Y Cov XY
=
+ =
=
+ = +
2
2

where c is a constant, X and Y are random variables and Cov is the covariance,
introduced below.
That the variance of a constant is equal to zero makes sense if we view the variance
as a measure of dispersion (or spread) about the mean. In the case where all the
values are the same, there is no dispersion. Likewise, that adding a constant to the
RV X doesn't change the variance is unsurprisingwe are simply shifting the
values of all data by the same quantity and making no change to the dispersion of
values. Multiplying each value by a constant c changes the variance by c
2
because
the variance has the dimensions of squared units.
Measuri ng Di spersi on
The variance is a statistic that measures dispersion. If most of the values lie near the
mean, the variance will be small. If the values are spread out over a wide range, the
variance will be large.
St andard Devi at i on
If we wish to measure dispersion in the same units as the values themselves, we use
the square root of variance, or standard deviation:
= Var X
44

Because the variance and standard deviation are expressed relative to the mean, a
variance is impossible to interpret unless we also know the mean. In particular, we
cannot compare the variance or standard deviation of one distribution to another
without taking into account the means of the distributions we are considering.
Coeffi ci ent of Vari at i on
A convenient statistic to calculate when comparing positive distributions is the
coefficient of variation (CV). This is also known as the relative standard deviation:
CV
m
=

The CV may be expressed in percentage units. If we compare two distributions, we
say that the one with the higher CV is more dispersed than the distribution with the
lower CV.
In mining applications the value of the CV is interesting to calculate early in our
assessment because it gives us a forewarning of potential difficulties. Values for CV
that are significantly greater than 1.0 are typical for sample grades from many
uranium, gold, tin mines. Some base metal deposits have CV's greater than 1.0.
Gold deposits can have CV's in excess of 2.0. The higher the CV is, the more
difficult subsequent geostatistical analysis and estimation will generally be.
The CV is sometimes expressed in percentage units (with CV = 100% being
equivalent to 1.0). This mode of expression relates to normal distributions, and
does not have a clear meaning for most mining (grade) variables.
Note that the relative variance
2 2
/ m is also used as a measure of relative dispersion.
It has a specific meaning when interpreting relative variograms, which we will
encounter later.
Non symmetric distributions present a problem, in the sense that the variance is
very sensitive to extreme values. Again, more robust parameters exist for
measuring dispersion: in addition to the range, there is also the interquartile range
(IQR) measuring the difference between the third and first quartiles.
The robust equivalent of the coefficient of variation is the interquartile coefficient
of dispersion which is equal to the ratio
IQR
Median

Ot her Moment s
The other two moments about the mean that you may encounter are:
S KEWNES S
The third moment about the mean is:
St andar d
Devi at i on
Variance has squared units.
The standard deviation has
the same units as the mean,
e.g. grade.
CV
A unitless measure of
relative dispersion that is
useful when comparing
distributions.
45

[ ]
( )
=
=
=
3
3
3
1
1
E X m
N
x m
i
i
N

For a symmetrical distribution, the third moment is equal to zero. An asymmetric
distribution with the tail of values at the large end of the range has a positive value
of
3
and is said to be positively skewed. Conversely, if the tail is at the small end of
the range,
3
will have a negative value, and the distribution is said to be negatively
skewed.
Geological variables often have skewed distributions. In particular, geochemical
variables that are measured in trace quantities, like precious metals and trace
elements, are frequently positively skewed.
Skewness is usually measured by a dimensionless quantity called the coefficient of
skewness:

1 1
3
2
3
2
= =

i.e. the third moment is standardised using the square root of the variance cubed.
KUR T OS I S
The fourth moment about the mean is:
[ ]
( )
=
=
=
4
4
4
1
1
E X m
N
x m
i
i
N

This moment measures kurtosis or peakedness. It has particular significance for
normal (Gaussian) distributions (we will discuss these in more detail later in this
chapter). In particular, for a Gaussian distribution the ratio:
2
4
2
2
3 =

=
The coefficient of kurtosis is defined as:

2 2
3 =
Consequently, the coefficient of kurtosis is equal to 0 (zero) for a Gaussian
distribution. Distributions that are more peaked than a Gaussian distribution have
positive values of
2
and are referred to as leptokurtic; conversely, distributions that
are less peaked than a Gaussian distribution have negative values of
2
and are
referred to as platykurtic. Kurtosis, although reported by many statistical programs,
is not particularly meaningful for skewed distributions.
Sk ew ness
A indication measure of
skewness can be gained
from examining the
histogram! The coefficient
of skewness is very non-
robust (cubed terms).
Another good measure is to
see if the median exceeds
the mean (positive skew) or
vice-versa (negative skew).
Kur t osi s
Highly non-robust and not
very meaningful for most
grade distributions.
46

The Box Pl ot
A useful graphical tool summarising the major statistical characteristics of a dataset
and allowing easy comparisons between data sets is the Box Plot. In general, it
shows the smallest and highest values, the first and third quartiles and the median
(see figure 2.3)

Min-Max
25%-75%
Median value
Box & Whisker Plot
-2
0
2
4
6
8
10
12
14
CU1 CU2

Figure 2.3. Box and whisker plots are a useful way of comparing duplicate assays, or different data sets.

Covari ance and Correl at ion
Another (very important) property of the variance can be stated:
+ ar Var X Y Var X V Y Cov XY + = + 2
where Cov[XY] is the covariance between X and Y. The covariance is defined:
[ ] ( )( ) [ ]
Y X
m Y m X E XY Cov =
where m m
X Y
, represent the means of the RV's X and Y respectively. The
covariance is also sometimes denoted
XY
.
Note that a property of the covariance is:
Cov XY Var X Var Y
This means that the ratio:
47

Cov XY
Var X Var Y
XY
X Y

usually known as the correlation coefficient is always between -1.0 and 1.0. The
covariance is thus easily understood as a non-standardised correlation coefficient.
The correlation coefficient measures the mutual relationship between two variables.
In particular:
1. A positive value of indicates a tendency for X and Y to increase
together (sympathetically).
2. A negative value of indicates a tendency for large values of X to be
associated with small values of Y (i.e. X and Y vary antipathetically).
3. When equals 1.0, there is a perfect linear relationship between X and
Y. The relationship has the form:
Y X = +
1. When X and Y are independent, their correlation coefficient is equal
to 0 (zero).
2. Note! The converse in generally not true, i.e. the correlation coefficient
can be 0 for X and Y not independent.
The covariance is equal to zero in the case of independence. The covariance can be
written:
Cov XY E XY E X E Y =
Linear Regression
In many geological and mining applications, it is interesting to consider the mean
value of one variable Y when the other variable X is fixed. This mean represents
the best possible prediction of Y by a function of X. The most traditional way of
establishing such a function of X is to use a least-squares procedure to establish the
line:
Y b aX = +
such that the sum of squared deviations about this line are minimised. Since we are
using a linear function of X, this regression is called linear regression. A couple of
useful formulae for linear regression are for the slope a:
Covar i anc e
The units of covariance are
squared. To easily grasp the
meaning of this statistics it is
best to standardise it by the
standard deviations of the
two variables of interest.
This standardised version is
the correlation coefficient.
48

a
Cov
y
x
yx
x
= =

2

and y-intercept b:
b m a m
y x
=

Figure 2.4: Regression lines for a bivariate Gaussian distribution

Note that E Y X x ( | ) = reads expected value of Y given X. It is a straight line
passing through the centre of gravity (m
x
, m
y
), which cuts all vertical secants to the
ellipses at their mid-points. It can be drawn easily by drawing one ellipse and
joining the two points where it admits a tangent parallel to the coordinate axis 0y.
Similarly the regression of X on Y is:
E X Y y m y m
x
x
y
y
( | ) ( ) = = +

Note that the two regression lines are different.
49

The fact that the regression is linear is really a property of the normal distribution.
In order to confirm this, let us consider the case (useful in practice as an
approximation for grade distributions) of two variables X and Y jointly lognormal.
This means that (lnX, lnY) is bivariate Gaussian.
For complex bivariate distributions (not lognormal), it is often impossible to
express the true regression or conditional expectation. Such bivariate distributions
are the usual case in geological and mining applications, especially for grades. As a
simplification, we might want to look for a linear relationship between the two
variables. The most traditional way for doing this is to use a least-squares
procedure:
E Y a bX ( ) = +
such that the sum of squared deviations about this line are minimised. Since we are
using a linear function of X, this regression is called linear regression. The model
underlying the linear regression is the following:
Y a bX
i i i
= + +
where X
i
is the value of the independant variable X in the ith case (the ith sample),
Y
i
is the response for the same case, the
i
are independant gaussian variables with
mean 0. and variance
2
.
The parameters a and b are estimated through the least square procedure. An
indicator of the quality of the linear regression is the coefficient R
2
which expresses
the percentage of the total variability explained by the regression. The closer this
coefficient is to 1., the more significant the linear regression is.
St at ist ical Tests
In sampling problems and other geological situations we may be faced with two or
more sets of values corresponding to differing sampling/assaying techniques. An
important question is whether the differences between replicated data sets (that
always exist to some degree) are significant. There exist statistical tests precisely
designed to answer this.
The first step in conducting a statistical test is to specify the possible alternative
conclusions we want to test; for instance, we might have the following alternatives:
H
0
: The difference between the two means is 0.
H
1
: The difference between the two means is not 0.
Note that these represents what is known as two-sided alternatives. We could also
define one-sided alternatives with H
1
being for instance: the difference between
means is positive. H
0
is called the null hypothesis of the test.
Li near Regr essi on
The linear regression is
equivalent to the conditional
expectation for a bivariate
Gaussian distribution (i.e.
both variables are normally
distributed).
50

We then need a statistical decision rule specifying, for each possible sample
outcome, which alternative should be chosen. This rule is in general based on a
number calculated from the sample and called test-statistic. The range of values for
which the alternative H
0
is accepted is called the acceptance region. The range of
values for which the alternative H
1
is accepted is called the rejection region.
Note the vocabulary used: a statistical test is never able to prove an hypothesis, because it
deals with a limited number of samples. There is always the risk of making the
wrong decision.
The risk of of rejecting the null hypothesis when it is actually true ( Type I error )
is called the level of significance.
A Type II error ( risk) consists in accepting H
0
when it is actually false. In general,
the risk is the more serious. In fact, the alternatives are often defined in such a
way that the type I error is the more serious.
The choice of the test statistic depends on what is tested and the sample available.
In general, we distinguish two broad categories of tests: parametric tests based on the
assumptions that the samples follow a particular distribution (usually normal) and
are independent, and non parametric tests for which the assumptions are much less
stringent.
As a consequence, parametric tests are more powerful but less universally
applicable. In mining applications, it is clear that most of the time, the hypotheses
required by parametric tests are not satisfied (spatial correlations exist, and the
distributions are not Gaussian). When the number of samples is large, nevertheless,
the distributional hypothesis loses strength because of the Central Limit Theorem
that ensures convergence of the mean towards a Gaussian distributed value. The
Central Limit Theorem tells us that if we consider a sequence of independent
Random Variables Z Z Z
n 1 2
, ,..., , with the same distribution, the sequence
defined by:
S
Z m
n
n
i
i
n
=

=
( )
1

converges towards a variable with a Gaussian distribution with mean zero. The
convergence is ensured even when n is relatively small.
There are an enormous amount of statistical tests. Many of them are described in
the standard statistical textbooks (as cited in the references). We limit ourselves to a
few tests we have found useful in studying sampling problems.

St at i st i c al Test s
There are many other tests
that might be useful in
particular applications. The
reader is referred to any
standard text on statistics, or
to Davis (1986) for
geological examples.
51

T-t est s
The t-test is probably the most common parametric test to evaluate the differences
in means between two groups. There are two versions of it:
1. T-test for independent groups (e.g. comparing results from two
drilling campaigns with RC and DDH, although it is often difficult to
apply any statistical test in this case, because of spatial correlations).
2. T test for paired samples (case of replicate or duplicate samples ).
Many statistical software packages, like Statistica, report a probability p
measuring the extent to which the sample data are consistent with H
0
.
The smaller p, the less acceptable H
0
.
Mann-Whi t ney t est
This test is the non-parametric equivalent of the t-test for independent groups. It
actually tests for differences in average ranks when mixing the data of the two
groups.
Wi l coxon mat ched pai rs t est
This is the non-parametric equivalent of the t-test for dependent (paired) samples.
It tests whether the median of the differences between paired samples is nil.
For other non-parametric tests refer to Meddis (1984).
Common Dist ribut ions
Some distributions have particular utility in geostatistical and resource estimation
practice. We list a few properties of the Gaussian or normal distribution and the
lognormal distribution for reference. For further details, refer to any of the statistical
texts listed in the references.
Gaussi an (Normal ) Di st ri but i on
The Gaussian distribution has a probability density function:
( ) f x e
x m
=

1
2
1
2
2

where m is the mean and
2
is the variance. A normal variable is often denoted by
( ) N m,
2
. The normal cumulative distribution function is tabulated in most
statistical textbooks, and by using such tables we can make statements like:
There is approx. a 90% chance that X lies in the interval [m1.645]
There is approx. a 95% chance that X lies in the interval [m1.96]
T-Test s
This test evaluates the
difference between tow
means.
52

There is approx. a 98% chance that X lies in the interval [m2.326], etc.
The authors are not aware of any mineral deposits possessing distributions that are
normal. However, the normal distribution is of great importance in statistics and
geostatistics for the following reasons:
1. Some element distributions present a normal histogram if we take
logarithms (see next section).
2. The normal distribution has useful applications as a deskewing
transformation. It is possible to transform any unimodal distribution to
a normal distribution, either graphically or by Hermite polynomial
expansion (see Hohn, 1988). The transformed values may be
manipulated in interesting ways and form the basis of a number of
advanced geostatistical techniques, including:
o Disjunctive kriging (Matheron and Armstrong, 1986)
o Turning bands conditional simulation (Journel and Huijbregts,
1978) (and some other Gaussian based methods).
o The discrete Gaussian change of support model (Guibal, 1987),
and applications including Uniform Conditioning.
Lognormal Di st ri but i on
In many earth science problems the distributions tend to be positively skewed (i.e.
skewed to the right). This means that there are a small, but significant number of
quite high values. In particular, this type of skewness is common for elements that
have relatively low abundance, for example trace elements in soil surveys. The
distributions of precious metal deposits are often positively skewed.
For positively skewed distributions, it is sometimes found that the logarithms of
the values tend towards a normal distribution.

Defi ni t i on
If a transformation to logarithms
5
results in a distribution that is normal, then the
distribution of X is said to be lognormal. Note that if log Y has a normal distribution,
then so does log
e
Y (log
e
being the "natural logs", otherwise denoted as ln Y). In
fact, it does not matter which base we use, so long as we are consistent. We state
the formulae in terms of log
10
in this section.

5
Note that there are situationsin both classical statistics and in geostatisticswhere the technique of
taking logarithms is used purely for the purpose of deskewing the distribution. In such cases there is no
implication of lognormality. We will encounter this approach later, when considering variography, for
example.
Lognor mal i t y
One of the most misapplied
aspects of statistics in earth
sciences and mining has
been to presume that grade
variables have lognormal
distributions. In general,
they do not.
53

The South African (Witwatersrand) gold deposits are usually quoted as the
classical example of lognormal mineral grade distribution. Many other
geochemical variables in the earth sciences have distributions that are, at least
approximately, lognormal.
The density function of the lognormal random variable Y is:
f y
e
y
y
( )
log
exp
log log
=

2
1
2
2

where is the median of the distribution, i.e.

= 10
where is the mean of the logarithms of the Y values (i.e. the mean of the values
x=log y) and is the standard deviation of the logs. A lognormal distribution is
completely specified by the two parameters and and is consequently often
referred to as a two parameter lognormal distribution.
The mean of the lognormal distribution is not the mean of the logarithms. The
mean m and the variance s
2
are defined:
( )
m
s m
=
=
10
10 1
2
2
2
2 2

Test i ng for Lognormal i t y/Normal i t y
The following tests are commonly employed:
P R OB AB I L I T Y P L OT T I NG
The traditional method in mining and geology applications involves plotting of the
cumulative frequency distribution on probability / log-probability paper. If this
plots as a straight line, the distribution is normal/lognormal.

Q- Q P L OT
Another approach involves plotting a scatterplot of the values of the selected
variable against the values expected from the tested distribution (normal or
lognormal). One way for doing this is to first rank the observed values x
i
, and
from these ranks (which give immediate access to the cumulative frequency)
calculate the equally ranked y
i.
based on the assumptions that the data come from a
normal (or lognormal) distribution. If the scatterplot of x
i
against y
i.
is linear, then
the experimental data can be said to exhibit a normal ( or lognormal ) distribution.
54

This scatterplot is often called probability plot or q-q plot
6
.
In fact, a q-q plot can be used to test the fit of any theoretical distribution. This plot
is also possibly useful in assessing the existence of multiple populations (as revealed
by clear changes in slope
7
). With very skewed experimental distributions, it can be
use for defining top-cuts or correcting high values: one possible criterion is to
look at the value above which the distribution clearly departs from lognormality
and use this value as a starting point for corrections (see David, 1988 for examples).
Figure 2.5 shows an example of q-q plot used for testing lognormality.
Probability Plot
LOG_CU
Value
E
x
p
e
c
t
e
d

N
o
r
m
a
l

V
a
l
u
e
-4
-3
-2
-1
0
1
2
3
4
-6 -5 -4 -3 -2 -1 0 1 2 3

Figure 2.5 Example of q-q plot used for testing lognormality, copper grades in a porphyry Au-Cu deposit.
C HI - S QUAR E GOODNES S OF F I T T ES T
The Chi-square goodness of fit test. The
2
test is a general test for testing a fit to
a distribution. Since it is given (usually with a worked example) in most statistical
textbooks, we won't detail it here in our brief review. The reader can find a fully
worked example of the
2
test for the lognormal case in Sinclair (1984).
Three Paramet er Lognormal Di st ri but i on
If plotting the cumulative frequency on log-probability paper results in a curve that
deviates from a straight line this may constitute evidence of skew under lognormal
conditions. In such a case, an additive constant a may transform the distribution to
lognormality. Such a distribution is refereed to as a three parameter lognormal
distribution. This distribution has been widely applied in South Africa for gold, and
an example is given by David (1977, p14).

6
q-q stands for quantile-quantile, as we plot the quantiles of the experimental distribution against the
quantiles of a normal or lognormal distribution
7
Caution must be exercised with these approaches. The fact that our plot deviates from that expected if
the data follow a particular distribution may mean that our data follow another (less mathematically
simple) distribution. Also, we must make sure that we do not mix sample support when constructing such
plots (see later).
55

Note that although we may have lognormal conditions in a mineral deposit (or
group of deposits) several lognormal distributions may exist. This is the case in
some South African gold mines. For example, on the Witwatersrand, the additive
constant a varies from mine to mine. Similarly, several different zones, or discrete
veins, within a single deposit may have different lognormal distributions.

Si chel ' s t -est i mat or
The conventional way of estimating the mean for the distribution of sample grades
is to use the arithmetic mean. However, in the case of a lognormal distribution
when we only have a small number of samples, the arithmetic mean tends to
overestimate the population mean. This is because of the small number of very
high values that we can obtain when sampling a lognormal distribution.
Sichel (1952) proposed his t-estimator to obtain an less biased estimate of the mean
in such circumstances. Sichel's t is defined as:
t e V
M
= ( )
where M is the mean of the natural logs of the sample values and ( ) V is a
complex power series that is tabulated by Sichel (1952) and David (1977), both of
whom give worked examples.
Note that Sichels estimator is designed for a small number of samples (say less
than 50). In the case of a lognormal distribution, the Sichel estimator should give a
value that is less than or similar to the arithmetic mean. Not infrequently, the Sichel
estimator provides a very similar estimate of the mean to the arithmetic mean. In
other cases, however, the difference may be quite large.
If we obtain a Sichel value that is much larger than the arithmetic mean we
should suspect our distribution is not lognormal! It is emphasised that the Sichel
t may give unreliable results if the distribution is not lognormal. A careful test
for lognormality is recommended prior to using this method. David (1977)
gives a worked example (from Sichel's paper, in fact).
Si c hel s t
Has strong assumptions
relating to lognormality,
independence and small N.
C H 4 S A M P L I N G
56

4: Sampling
Sampling is one of the basic operations of the human mind.
It does not receive the attention it deserves.
Pierre Gy, in the forward to Pitards 1989 book
What is t he Object ive of Sampling?
Lets begin with a real situation. When we drill an RC (Reverse Circulation) drill
hole, for each intervalsay 1mof material drilled we should deliver to the
surface all the material from the cylindrical volume under consideration. Problems
of sample loss (recovery), sample contamination, etc. are in the domain of drilling
technology, which we discuss further, below. With the right equipment and good
drilling we can overcome such problems in most cases.
The problem considered here, then, can be stated thus: we recover say 30kg of
disaggregated material from a 1m RC drilled interval: let us call this our lot. How
should we select a portion of this materialour samplefor submission to the
assay-lab?
The statistical basis for addressing this problem is not complex: we need to select
material in a manner such that:
On average the grade of the sample is equal to the grade of the lot (this is
the non-bias criteria); and
On a sample-by-sample basis, the squared difference between the grades of
duplicated samples should be minimised (this is the criteria of maximum
precision).
Chapter
4
57

In practice, we can never reduce this squared difference to zero it is a measure of
the dispersion or spread of sampling errorsunless the size of the sample is equal to
that of the lot. Unless, that is, we take the lot.
Equi probabl e Sampl i ng
To obtain a good sample we need to use a sampling device that ensures that each
particle in the lot has an equal chance of getting into our sample. Such a sampling
device is said to be equiprobable. It should be clear, for example that a grab or
spear sample
8
gives no chance to particles to be included in our sample if they are
physically outside the grabbed or speared volume.
A riffle splitter is the best practical equiprobable sampling device for use with RC
drilling. The technicalities of riffle splitters are elaborated later. Other techniques of
RC sampling such as grab sampling and spear or pipe sampling are
demonstrably not equiprobable. This results in poor sampling precision, and
(perhaps worse still) in bias. Comparison of pipe splitting versus riffle splitting at a
Victorian gold deposit suggested a dramatic reduction in sampling error: the mean
squared difference between duplicated riffle splits being 80-85% lower than that
calculated for duplicated spear samples.
Grab samples are much worse than spear samples, in principle.
A Si mpl e St at ement of t he Probl em
If the mineralisation is very fine and uniformly disseminated (in other words, all
particles in our lot have similar grade) the sampling problem is simple: this is the
case for some base metal mineralisation, for example. As the coarseness of the
mineral phase increases, and the inhomogeneity of grade distribution between
particles increases, for example the case of coarse, particulate gold, the impact on
the sample grade of a few very high-grade particles within the sample is increased.
In these circumstances, progressively larger samples are required and there is an
established literature to guide us in this matter (see references). These problems are
in the domain of particulate sampling theory, which we introduce in this course.
Note also that for high nugget gold mineralisation the grade of a drilled
intervalperhaps even if we assay the whole lotwill be quite poorly correlated
with the grade of the surrounding mineralisation. In other words, our ability to
discern high vs. low-grade zones based on drilling is decreased. In such a case, we
cannot safely estimate the grade of small blocks, but good sampling may enable us
to make unbiased estimates of global grade. These problems are the domain of
geostatistics (again, see references).

8
Spear sampling involves drilling the bag of drill chips/cuttings with a pipe or spear.
Equi pr obabl e
Literally: equal probability.
An equiprobable sampling
device gives an equal chance
of being selected (or not) to
each particle.
Summar y
Sampling error can be
significantly reduced by
using equiprobable sampling
devices such as well-
designed riffle splitters.
58

Types of Sampling in Open Pit Grade Cont rol
Estimating block grades from sampling data is an activity that is fraught with
difficulty. Most classical statisticians would regard the data for any grade control
problem as dangerously inadequate. A 10m x 10m RC grade control grid equates to
sampling of about 1/25,000
th
of each 10m x 10m area. The small volume sampled
is better appreciated if we express this as 0.004%.
The main decisions made about allocating material to ore or waste (or intermediate
stockpiles) are taken at the grade control stage. The quality of the grade control will
thus impact profoundly on the economics of the mine.
Delineation of ore boundaries above a given cut-off is a difficult problem for the
following reasons:
1. The grade measured in one hole can be well correlated or poorly
correlated to the grade of the surrounding mineralisation (the block
within which our sample is located). This correlation between sample
and block grades is measured by the variogram and in particular the
nugget effect and any short-range structures (these points are detailed
further, later in the course).
2. The grade we have from our sampling may not actually represent the
grade of the sampled material very well. This is generally due to a poor
sampling protocol and has two implications:
o Contributing to an incorrect grade estimation of the
surrounding block.
o Increasing the proportion of nugget effect on the variogram,
because the increased sampling variance due to poor sampling
protocol adds to the nugget. This always decreases the
precision of estimation, in extreme cases (pure nugget) it
renders local (block) estimation unfeasible.
3. The resultant error will always overestimate the higher grade blocks
and underestimate lower grade blocks (conditional bias).
In fact, it is a general case that grade control cuttings are either not geologically
logged, or are logged in a very cursory manner (often by inexperienced geologists).
So it is the usual situation that ore-waste boundary recognition is highly reliant
upon the values obtained from sampled material. The quality of this sampling is
thus a key factor in determination of the overall quality of grade control.
The most common approaches to open pit grade control sampling are:
1. Sampling of blast hole (BH) cuttings.
2. Sampling of purpose-drilled production reverse circulation (RC)
drilling.
2 Types of Li e
There are two ways in which
a sample grade can mislead
us. The first is that it will be
imperfectly correlated to the
grade of surrounding
material; the second is that
the sample may not
represent the sampled
material in any case.
59

These two approaches are not equivalent in terms of sampling quality, and in
particular, there are a range of methods for sampling the cuttings from RC and BH
from which widely differing data quality can be obtained. In some circumstances,
other approaches (Ditch Witching
9
or channel sampling may be considered). We
look at each of these methods in detail, below. But first, we consider how to
compare different approaches.
Test i ng Di fferent Approaches t o Sampl i ng
Before deciding to adopt a particular approach to grade control it is advisable to
make quantified tests of each method considered. The main steps in such a test are:
1. Select a characteristic (or several characteristic) test areas. In general,
these should be large enough to allow proper statistical and
geostatistical assessment of the results. An area of at least, say, 50m x
50m will be required, usually a larger area is needed.
2. Sample the area by the different methods at a closely spaced grid (the
closest grid we can envisage for production grade control). Attempt to
implement both methods on the same spacing, but off-set (e.g.
paired holes), if possible.
3. Compare statistics and variograms for the different data.
4. Assess the selectivity on the basis of estimated block models for the
different methods. We consider this later in the course.
5. Rank each method according to the conventional benefit returned in
each case. Subsequent discounted cash flow analysis (DCF) can
complete the process and allow us to make an economic decision.
6. Use the variogram to determine appropriate drill spacing (again, we
consider this later on).
7. Use the variogram to perform tests of different estimation strategies.
Now we consider the main methods available for collecting grade control data.
Bl ast Hol es (BH)
Blast holes are open holes, generally drilled by a percussion rig. By open hole we
mean that the sample is returned via the annulus between the hole walls and the
drill rod. The potential for contamination, hole collapse and recovery difficulties is
significant in this type of drilling.
Percussion drill rigs are based on having a relatively slowly turning rock chisel or
hammer hit the rock face, with cuttings being brought to the surface by the return

9
A Ditch Witch is a modified trenching devices originally designed for laying telecommunications and
other cables.
Sel ec t i ng a Test
Ar ea
This is probably the most
difficult step. Choosing a
typical area is difficult and
requires careful geological
and geostatistical
consideration.
60

air. The down-the-hole hammer, if fitted, operates by air. Figure 2.6 shows
different types of non-core drilling.

Figure 2.6 Drilling methods. (After Hartley, 1994, figure 7).
General Charact eri st i cs of BH Sampl es
The general characteristics of blast hole samples may be summarised as follows:
1. Generally large samples, depending on hole size (although in some
small-pit operations, BH hole diameters are less than standard RC
holes). BH holes vary from less than 100mm up to greater than
300mm in large operations.
2. Vertical holes: angling is usually not an option. This is a concern if the
mineralisation in sub-vertical in grain.
3. Relatively rapid drilling (of the order of several hundred metres per
shift).
4. No additional drilling cost (BH have the primary purpose of blasting,
of course).
5. The drilling pattern will be dictated by blasting requirements.
6. Pronounced sampling difficulties: samples are often collected from
spoil heaps, or less frequently via dedicated riffle splitters. However,
such riffle splitters are usually not correct in design or implementation.
7. Potential biases by virtue of differential recovery, sample loss, sub-
drilling etc.
8. Generally only one sample is taken, representing the full depth of the
BH hole. We have little chance to take metre/metre samples with this
approach, so if vertical selectivity is critical, BH sampling can be a poor
option. This has the additional down-side that the variogram often
cannot be defined properly in the vertical (down-hole) direction from
bench-height samples.
61

9. We do not have data from benches below the current mining bench:
this reduces the precision of estimation in most cases.
The sampling problems with BH are daunting. The material in the spoil pile is
always granulometrically segregated, i.e. there is a stratified variation in particle
sizes. Further, the spoil pile is commonly asymmetric, which causes further
sampling difficulties. The spoil pile is exposed to the climate and this may result in
wind-blown winnowing of finer granulometric fractions. Rain can wash the pile
causing additional degradation of representivity.
The profile of the spoil pile is thus not symmetric, with cuttings collecting in the
pile based on random patterns which are influenced by changes in drilling
pressures. The grain-size typically coarsens downwards, with the coarsest fragments
tending to be deposited at the base of the pile and the fines at the top. This results
in a profile which does not facilitate representative sampling. These problems are
all exacerbated when the mineral phase of interest is relatively dense, e.g. gold, base
metals, uranium.
The sub-drill material (i.e. the material from the next flitch) generally accumulates
on the top of the spoil pile, which is particularly dangerous if grab sampling is
performed.
Approaches t o BH Sampl i ng
Most larger BH holes are sampled by:
1. Grab sampling from the pile. This is invariably disastrous due to
the granulometric segregation just discussed: a grab sample over
samples the fines, usually. It will also be biased because of sub-drilling.
A marginally more sophisticated approach is to attempt to scrape off
the sub-drill prior to taking a grab sample: but this is easier said than
done and all the other problems inherent in BH sampling are not
solved by this.
2. Sector pan sampling. A pie shaped sampling dish is placed at the
collar prior to drilling. This is better than a grab (or manual section)
sample, but still does not alleviate the difficulties associated with non-
representivity of the cuttings themselves. Furthermore, a very large
sector sample is often required, which has significant OH&S
implications for those handling the samples. Because large samples
must be collected, sampling preparation costs are increased. The
authors have seen sector pans used in incorrect ways: the pan must
always be radial to the spoil pile.
3. Pipe sampling: a spear or chute of some type is pressed into the drill
spoil pile. Often a number of such samples are taken and then re-
combined (this is called an incremental sampling strategy). Again,
problems of representivity of the cuttings arent addressed. In general,
such approaches can be very poor if there is a significant degree of
heterogeneity within the spoil pile (e.g. gold, phosphorous in an iron
BH Sampl i ng
In most cases it is
impossible to collect
unbiased, precise samples
from blast hole cuttings.
62

ore mine, etc.). May be acceptable in lower nugget situation (porphyry
Cu).
4. Riffle splitting: certainly the best approach, but in the case of blast
holes, especially larger diameter blast holes, the mechanics of mounting
such a splitter are not simple. When riffle splitters are in use, BH
sample cuttings are normally delivered to a cyclone via a stuffer-box at
the collar. Often, a Jones riffle splitter (which itself may be well-
designed) is then mounted directly under the cyclone. This effectively
means that only the central slots of the splitter are being used, and, as
we will explain later, this results in potentially very serious biases and
imprecision.
Ot her Consi derat i ons
There are some other significant aspects to using blast holes for grade control.
Unlike Ditch Witching or production RC drilling, BH drilling does not interfere
with the mining schedule. However, the time frames are consequently set by the
mining schedule. These may place enormous pressures on work efficiencies in a
grade control system, especially if adequate (read: time-consuming) sampling and
grade control practices are performed.
The time-gap between BH drilling and ore-waste allocation can be very short. In
some cases, as mine geologists may have experienced, it can contract to nothing!
The main problem with BH, then, is the inherently poor representivity of the
cuttings and the difficulty of correct sampling. If the sampling error is too high,
ore/waste misallocation may increase to unacceptable (perhaps economically
calamitous) levels. In this case, the sample becomes dangerous in the sense that it
incorrectly represents the sampled ground.
Reverse Ci rcul at i on Dri lling
RC drilling is where the drilling fluid travels down the outsides of the rods and
returns with cuttings on the inside of the rods. Dual tube RCwhich is what is
meant by the everyday use of the term RCgenerally means that the fluids pass
down to the face in the annulus between the drive rod and an inner, light-weight
rod. The cuttings are returned to surface inside the inner rod.
The principle advantage of RC over open hole methods is that the possibility of
smearing is significantly reduced. Originally, RC systems were used with
conventional down-the-hole hammers (DTHH), which required a cross-over sub
immediately above the hammer. This sub is a connection that took clean air from
the annulus to the centre of the hammer and then diverted the air and cuttings
returning outside the hammer back to the inside tube. This meant that, in effect,
standard circulation occurred for approximately 1.5m back from the drill-face
(Hartley, 1994).
However, in recent years face sampling hammers have quickly gained popularity.
In these systems, reverse circulation is maintained to the drill-face. Unless there are
RC Dr i l l i ng
Is usually significantly better
than BH sampling, but we
must justify the additional
cost and possible
interference in mining
schedule.
63

significant problems with ground conditions face-sampling systems are to be preferred over
conventional RC.
General Charact eri st i cs of RC Sampl es
The general characteristics of RC samples may be summarised as follows:
1. Typically, smaller samples than BH, depending on hole size (although
in some small-pit operations, BH hole diameters are less than standard
RC holes). The industry standard for RC is about 5.5 or 140mm.
2. We can drill RC at angles from about 45 degrees to vertical. This is a
benefit if the mineralisation in sub-vertical in grain.
3. Relatively rapid drilling (of the order of several hundred metres per
shift).
4. Extra drilling cost. On a particular project, we calculated this as about
+15% relative to BH in terms of the total cost of grade control for a
given drill spacing.
5. Unlike BH, where the drilling pattern will be dictated by blasting
requirements, we can plan our RC holes taking geology or other grade
control factors into account.
6. Fewer sampling difficulties compared to BH. Samples are generally
collected by dedicated riffle splitters, but unlike the case of BH, such
riffle splitters are more frequently correct in design and
implementation. We discuss this further, later.
7. Potential biases by virtue of differential recovery, sample loss, sub-
drilling etc. are reduced dramatically compared to BH.
8. We have the opportunity to take metre/metre samples with this
approach, so if vertical selectivity is critical, RC sampling can be a
much better option than BH. This has the additional advantage that
the variogram can thus be defined properly in the vertical (down-hole)
direction, unlike BH.
9. We can have data from benches below the current mining bench. This
increases the precision of estimation in most cases, and allows better
planning, scheduling and geological modelling. It also gives us valuable
forward information for designing mining or drilling contracts.
64

Approaches t o Sampl i ng RC
Good sampling of RC is generally possible, so long as samples are dry. A well-
designed, properly-used, riffle splitter is obligatory.
In the case of wet ground, riffle splitters may clog and cause contamination
problems. In such cases, due to the time-scales involved in grade-control, drying of
samples followed by disaggregation and riffling is generally not feasible.
Some kind of rotary splitting or multiple pipe sampling approach may be
necessitated. Be warned that these approaches are generally significantly inferior to
riffling, and care should be exercised in choosing particular rotary splitters or in
designing pipe sampling approaches.
Sampling and mining of wet ore creates many difficulties, and the best solution is
to have adequate de-watering programs in place. Quality grade-control is an
additional argument for implementing de-watering.
The higher quality of RC samples often means that a sparser sampling grid can be
used, which can virtually negate the additional drilling costs.
Aut omat i on of Sampl i ng
The sampling of RC can be automated with the right equipment, for example an
integrated cyclone/tiered riffle system produced by Metalcraft and other
manufacturers. This reduces costs and avoids the OH&S problems of handling
large sector pans, etc. A diagram of the Metalcraft device is given in figure 2.7.
RC for grade control is becoming a more widely used technique, especially in large,
low-grade operations. Because high-quality data results in a better, more confident
definition of the variogram, kriging will be more efficient than with BH data from
the same deposit. In addition, this better knowledge of the variogram makes
simulation approaches more feasible and reliable.
Wet RC
As a basis for reliable
resource estimates, wet RC
is questionable. Wet RC
samples are natures way of
telling us that we need a
diamond rig!
65

Figure 2.7: Metalcraft automated splitting system.

Rul es of a Good Ri ffl e Spl i t t er
1. Even number of slots. Hard as it is to believe, riffle splitters with an
odd number of slots do exist!
2. At least 12 slots.
3. Slots at least 1.5 x the 95% sieve pass diameter. This prevents excessive
hanging up of chips.
4. Parallel slots.
5. Slots must be of equal width (watch out for narrow end slots).
6. Feed the device slowly and evenly across all slots.
66

7. Keep splitters well-maintained: broken splitters allow communication
of material between slots or result in spillage.
8. Keep it clean: filthy, muddy splitters are prime candidates for causing
contamination.
Di t ch Wi t ch Sampl ing
A summary paper on the subject of Ditch Witching is Bird and Archer (1987).
Ditch Witching is suited to sampling of relatively soft materials, for example in
open pit operations where ore is highly oxidised (saprolitic). The machine is tractor
mounted and was originally designed to lay communication cabling.
Depending on ground conditions, trenching rates can vary from 0.5m/min to
more than 2m/min. Size range of sample material ranges from very fine (10
micron) up to about 20mm, and is dependent upon rock competency. The material
looks much like RC cuttings and has roughly the same kind of granulometry.
Trenches can be cut to about 1m in depth, and are usually about 150mm wide.
Therefore a large sample mass is obtained, which is good.
Displacement of sample along the trench is characteristically minimal but can be
monitored visually.
The trenching spoils run along either side of the excavated Ditch Witching trench.
Sampling of these is by various methods, the best probably being an oblique,
longitudinal sample along one of the spoil lines. Such a sample can be collected by
a piece of halved polypipe (this was the method in use for sampling of lateritic ores
at Boddington Gold Mines in Western Australia).
10

The depth of the trench leads to the most important qualification about Ditch
Witching: if there is a strong sub-horizontal control on mineralisation, the
geometry of sampling by Ditch Witching will be potentially inadequate.
Channel Sampli ng for Open Pi t Mi ni ng
In some open pit grade control sampling situations, sampling of drillholes or
Ditchwitch may not be feasible. An example of this is the Waihi Gold Mine in the
North Island of New Zealand, where the large proportion of epithermal clay
alteration minerals (some of which are swelling clays) make the physical process of
drilling holes very difficult. In fact, at Waihi, RC drilling has been tested and found
quite ineffective: holes block-off and drilling is tedious, expensive and returns
samples which are of questionable quality.
Blast hole sampling, we have already noted, has the disadvantage that the holes
cannot be inclined. If the mineralisation geometry is predominantly sub-vertical (as

10
We have heard of an instance where a riffle splitter was directly mounted onto a Ditch Witch, resulting
in an incident which the mine geologist described as akin to a machine gun going off in the pit.
Enough said
67

at Waihi) then a linear sample in the horizontal plane is preferable to vertical BH
drilling.
Horizontal sampling might of course be possible with a Ditch Witch, but in some
cases very hard vein material (for example, the highly siliceous epithermal veins at
Waihi) make Ditch Witching inadequate: the risk is to over-sample the softer
material and under-sample the veins.
In such circumstances, it may be possible to sample for grade control by excavating
a channel, typically cut using some kind of powered jack-hammer (e.g. Kango
hammer). This type of sampling is usually highly labour-intensive (thus, costly).
Cutting adequate channels is extremely difficult, primarily because the channel we
cut does not actually look like the channel we intended to cut (which should have a
constant cross-section geometry). This failure to cut a correct channel results in a
type of sampling error called delimitation error (Pitard1993).
So, in cutting a channel, we can fail to excavate to the design limits, we can over-
excavate in places and under-excavate in others. The width of the channel might
also vary along its length. Therefore, as with previously described methods of
obtaining grade control samples, we need strict quality control on the physical
collection of samples. Trained operators are required, and this will generally add to
labour costs.
It is possible, under supervision, for well-motivated, experienced, adequately-
trained grade control technicians to cut acceptable channels.
It must be emphasised that great care needs to be taken in collecting the sample
material from channels on a pit floor. In particular, we must instigate procedures
that minimise the risks of over-sampling coarser chips relative to the fines. In
effect, we will need to clean the channel out.
Underground Grade Cont rol Sampling
This is usually by one or more of the following methods:
1. Chip sampling of faces and/or walls.
2. Channel sampling of faces and/or walls.
3. Grab samples of blasted, broken materials.
4. Sampling of drilling sludges from underground blast holes.
5. Purpose drilled holes.
Channel Sampl i ng
Cutting adequate channels is
extremely difficult, primarily
because the channel we cut
does not actually look like
the channel we intended to
cut. This is delimitation
error.
68

Face Sampl i ng
Dedicated samplers or geologists collect the face samples underground. Relying on
miners requires judgment, but cannot be recommended in general.
Often only every second or third round or face is sampled. Intermediate rounds are
sometimes assigned assumed grades from previous faces. Sometimes, when a face
is not sampled it is because it cannot be accessed (is not rock bolted, for example).
Rounds that are not face sampled may be grab sampled off the broken dirt. We
comment on grab sampling, below.
Taking line chips from faces or walls is an attempt to mimic channel sampling.
Channel samples, when correctly cut, are superior samples.
Since we know that face sampling is very difficult to do well, we need robust
protocols, good samplers and excellent management/supervision of this process.
It is rare that any type of interpolation is performed with underground face
sampling data, though it may be feasible.
The samplers should record sample locations in a neat and practical format. These
should always tie in (or be referenced to) good quality geological face mapping.
Dril l i ng Met hods
Sampling of various kinds of underground drilling is also often used for grade
control. Such sampling should be carefully observed. It usually consists of
collecting a wet slurry in a tray or a bucket and scooping sample (by means of a
hand-or literally by hand). It may strike a rubber mat at the collar and then free-fall
into the collection tray/bucket. There is usually the attendant problem of material
being splashed around and lost. Such losses are often differential losses with
respect to granulometry and density, and can be expected to introduce biases.
Sampling of underground drilling is almost always the drilling contractors
responsibilitywhich can be problematic from a QC point of view.
So we should be concerned about potentially serious bias and imprecision in
underground drilling sampling: certainly we should not sample very shallow or
down holes. The collection system should be standardised and the procedure
documented.
We need to measure the quality of sampling processes. This will necessitate
duplicate sampling of a significant number of underground holes. It is suggested
that entire rings be duplicate sampled (this way two alternative images of the
ore/waste boundaries are generated). The two samples need to beas close as
practically possiblecollected in identical fashion.
Ot her Consi derat i ons
We should remain open-minded about ways to improve sampling because
underground grade control sampling is very difficult to perform properly and the
Fac e Sampl i ng
Even with the difficulties of
collecting ideal face
samples, they are much
superior to grab samples of
broken dirt.
Measur i ng
Per f or manc e
We should always duplicate
sampling to allow proper
QA/QC procedures.
69

economics of most operations are highly sensitive to it. If technical innovation is
required, we should investigate the alternatives.
We should avoid grab sampling broken dirt wherever we can. This type of
sampling is a disaster for low-grade materials (with high nugget) like gold. If it
means that we need more samplers, or we need samplers to work more shifts, then
this is very cheap compared to the costs of misallocation caused by grab sampling.
Sampling of broken ore lots where the top-size is much larger than about 25mm is
a extremely difficult task, usually involving very large samples and incremental
sampling strategies (i.e. the taking of many samples). Broken ore in underground
mines may have a top-size that exceeds the dimensions of a Volkswagen Beetle
11
!
Its simply not possible to sample such material in an equiprobable manner.
The Rol e of Geost at i st i cs
The variograms of the underground sampling data should be calculated and
reported and directional variography is also important. The variography of HW to
FW composites (i.e. accumulation variables, see Chapters 6 and 7) can be very
interesting and should be calculated. Often, underground grade control data is not
adequately statistically assessed.
In fact, a first step in assessing the quality of existing U/G data should be to
perform rigorous variography of the data.
Once we have variogram models we can start to address, for each deposit, such
issues as:
1. How can we measure improvements in sampling and assay (i.e.
measure reduction in the contribution of these to the nugget variance)?
2. Do we need to sample every face/ring? How many do we need to
sample?
3. Are we collecting enough samples on each face? Are they large enough?
4. How should we use this data to best estimate for ore allocation or
stope design purposes?
5. Can the grade control data help us to establish appropriate drilling
geometries/spacings for near-mine extensions or new resources? In
particular, the variogram can allow us to calculate estimation variances
to establish global confidence intervals on the mean grade of
intersected mineralisation.
6. What can the grade control data tell us about the spatial distribution of
grade at depth? In other words, how can we best integrate this data
into our overall geological picture of each deposit?

11
Thats a bug if youre North American
Gr ab Sampl i ng
Sampling of broken ore is
generally impossible. Unless
the grade is very
homogeneously distributed,
we cannot get a reasonable
sample from this type of
material.
Var i ogr ams
Variograms are dealt with in
the next chapters. A
variogram measures spatial
variability and is a key tool in
assessing sampling data.
70

Pract ical Int roduct ion t o Sampling Theory
The subject of sampling is almost entirely omitted from the syllabus taught to
geologists and mining engineers in Australia and we suspect elsewhere. This is
unfortunate, given the fact that most of the important economic and technical
decisions made by geologists and mining engineers in an operating mine are based
on data collected by a sampling process of some type!
An understanding of the importance of sampling practice and sampling theory is
critical in the design and implementation of correct grade control.
During the 1950s and 1960s Dr. Pierre Gy formulated a generalised Theory for
the Sampling of Particulate Materials. This theory developed in parallel with Prof.
George Matherons development of the Theory of Regionalised Variables (which is
the basis of modern geostatistics), and not without some cross-fertilisation.
Gys Sampling Theory is the only worked-out theory for particulate sampling, and
it is general enough to be applied to most of the sampling problems seen in a grade
control context.
However, the application of this theory has been limited in the mining industry,
largely because of the technicality and mathematical prose of Gys book (Gy, 1982).
The publications of Dominique Franois-Bongaron and Francis Pitard (see
references) have provided more accessible presentations of Gys theory. The paper
of Dominique Franois-Bongaron and Pierre Gy (2001) is a particularly good,
and up-to-date, starting point.
A second problem with the acceptance of Gys theory has been that, to quote
Assibey-Bonsu (1996):
in spite of its renowned theoretical validity, Gys theory has been
found to have some limitations in its implementation, which are
mainly due to the misapplication of the model
This course cannot substitute for a sampling course
12
, but sampling is such a critical
activity (and source of serious error) that we present a digested summary here.
Component s of t he Tot al Sampl i ng Error
In general, the sample grade the lab returns to us is not, in fact, the true grade of
the material delivered to the lab. There is always a sampling error, and this error can
be viewed as being made up of several components:
1. Fundamental Sampling Error (FSE): due to the irregular
distribution of the economic mineral in the lot to be sampled. The
FSE is the smallest achievable residual average error, i.e. the
component of total sampling error that can never be totally eliminated.

12
The authors regard attendance at a specialised sampling course as a fundamental step for mine
geologists dealing with exploration, grade control or resource/reserve issues.
Sampl i ng Theor y
One might say that
particulate sampling theory
is about the internal
architecture of the nugget
effect.
71

2. Segregation and Grouping Error (SGE): due to lack of
homogeneity of the lot and grouping of the fragments by increments
in the sample. To quote Dominique Franois-Bongaron no matter
how counter intuitive (the) idea may appear, it is close to impossible to successfully
homogenise a lot of broken ore solely by mixing. The usual case is that
attempts to homogenise a lot by mixing result in the opposite effect:
we segregate the lot because of a variety of physical processes, chief
among them gravimetric separation of grains and grain-sorting by size
(granulometry). With very fine materials, static electric effects may play
a role, with some clayey materials the relative adhesion (stickiness) of
particles is important. Note that the SGE is difficult to quantify and its
magnitude may exceed that of the FSE.
3. Analytical Error: The variance of differences between duplicate
analyses is equal to twice the variance of the analytical error plus the
FSE for sampling an additional aliquot from the pulp.
Note also that operator errorthat is, using the correct sampling device
improperly, or failing to follow a prescribed sampling procedureis a serious issue
in sampling, because correctly designed sampling devices that are not used in the
proper manner can result in serious biases or large degrees of imprecision.
Gys Theory of Fundament al Sampli ng Error
The following presentation is based in part on that of Winfred Assibey-Bonsus
excellent 1996 summary paper and on the various papers of Dr. Dominique
Franois-Bongaron (see references).
Gys original model for the fundamental sampling error (FSE) can be written:
R
s l
n
M M
f g c l d
2 3
1 1
=

where:
R
2
is the relative variance of the FSE.
d
n
is the nominal top-size of the fragments in the sample. This is the maximum
particle size in the lot to be sampled. In practice, d
n
is taken as the mesh size that
retains 5% of the lot being sampled (i.e. the 95% pass diameter). The formula for
FSE presumes that d
n
is expressed in centimetres (cm).
f is the particle shape factor. This is an index which varies between 0 and 1 in
most cases. In practice, most values range between 0.2 and 0.5, depending on the
shape of the particles. For most ores, f is assigned the value 0.5.
g is the granulometric factor. Granulometry is a term that describes grain-size
distribution. The granulometric factor, g , can, like f , assume values between 0
Segr egat i on
This error is serious in many
practical sampling systems
and may in fact be the
largest type of error.
72

and 1. Low values of g indicate a wide range of grain sizes within the lot, whereas
high values of g denote relative uniformity of grain-size. A value of g equal to 1.0
indicates that all the particles in the lot are of identical size ; for most practical
situations, a value for g of 0.25 is realistic.
c is the mineralogical composition factor, and can be expressed:
( )
[ ]
c
a
a
a a
m g
=

+
1
1
where:
a is the decimal proportion of the mineral.

m
is the density of the valuable constituent.

g
is the density of the gangue.
a refers to the decimal proportion of the ore mineral. Note that densities are
specified in grams per cubic centimetre (g/cm
3
).
For example, for zinc, occurring in pure sphalerite (ZnS), an assay of 5% is
equivalent to a decimal proportion of 0.075:
a =
+
=
64 32
64
5
100
0075 .
Note also that:
c
t
m
=

where t is the grade of low-grade ores, for example, gold. It is
important to note that t is expressed as a proportion, i.e. grams/gram; not
grams/tonne. Hence a grade of 10 g/t is expressed as:
t
g
g
= =
10
1000000
000001
, ,
.
M
s
is the mass of the sample, measured in grams.
M
l
is the mass of the lot, measured in grams.
l is the liberation factor, which is a number (once again) varying between 0 and
1.0. Gy assumes that the liberation factor, for unliberated particles, is:
l
d
d
n
=
0

73

where d
0
is the liberation size, i.e. the maximum particle size that ensures
effectively complete liberation of the mineral. Note that d
0
is measured in
centimetres (cm).
The result we calculate for the FSE is very sensitive to the value assumed for this
liberation factor (we discuss this more, below).
A Si mpl i fi cat i on
In almost all grade control situations, M
s
is much smaller than M
l
. Because the
term
1
M
l
in this case approximates zero, the condition that M
s
is much smaller
than M
l
logically leads to a simplification of the formula for FSE:
R
n
s
f g c l d
M
2
3
=

More About t he Li berat i on Fact or
Gy proposed an approximation to obtain a value for the liberation factor, l. As
stated above, the calculation of FSE is highly sensitive to the value of l we employ.
The empirical estimate proposed by Gy is, as previously noted:
l
d
d
n
=
0

It is important to note that this empirical result, which has been applied
indiscriminately to all types of ores, was obtained by experiment from specific ores
which were high-grade. By high grade we mean that average grades exceed several
percent.
Low grade ores (gold, PGE, uranium, diamonds and some copper and nickel
mineralisation) are typical in large-scale, modern mining operations. The general
use of Gys approximation for l can, especially in the case of low grade ores,
produce results that are meaningless and this has led to many practitioners
abandoning Gys model (Franois-Bongaron, 1996). Winfred Assibey-Bonsu
(1996, p290) gives the following example:
Take, for instance, the use of Gys model (based on Gys empirical
liberation factor) in the calculation of a minimum sample size for a
typical South African gold mine in production. Assume a top particle
size of 13cm. With a gold grade of 5 g/t and a gold density of 19
g/cm
3
, the mineralogical factor, c, is:
c
density
grade
= =
+
38 10
6
. g/ cm
3

Li ber at i on f ac t or
The liberation factor is
critical is correct application
of Gys formula.
74

With grade expressed as a proportion, as previously explained.
For a gold grain top size of 75m (i.e. 7.5 x 10
3
cm), Gys
empirical liberation factor is:
l
d
d
cm
cm
n
= =

=
0
3
2
75 10
13
24 10
.
.

At a relative precision of 10%, i.e. a variance of 0.01 g/t
2
, the use of
the above computed parameters gives a minimum sample mass of
2,507 tonnes. For a typical production rate of between 1,000t and
10,000t per shift, this minimum sample mass is practically
unacceptable.
Assibey-Bonsu is not the first to report this kind of result, and those interested are
referred to the papers of Franois-Bongaron for further details. Franois-
Bongaron and Gy (2001) give an equally ludicrous result when a particle size for
gold is calculated to be smaller than an atom of gold!
At this point, many geologists or mining engineers would abandon the theory, but
perhaps we should carefully consider the reasons for such unacceptable results.
Franois-Bongarons Modified Sampling Theory
Extensive research in the 1990s by Dr. Dominique Franois-Bongaron proposes
an alternative model for the liberation factor, l, from which better results, especially
in the case of low-grade ores, can be obtained.
The model proposed by Franois-Bongaron is as follows:
l
d
d
n
b
=

0

We recall that the formulation of Gy is:
l
d
d
d
d
n n
= =

0 0
05 .

So the difference between the modified l of Franois-Bongaron and the original l
of Gy is simply the variable exponent b, which Franois-Bongaron proposes can
be experimentally calibrated for specific ores.
For example, for gold mineralisation, in most cases, the exponent b is found to
have a value of about 1.5. This clearly will result in a different estimation of FSE.
Moder n Theor y
Dominique Francois-
Bongarcon has modified the
theory of Gy to make it
more practical.
75

Since the value for b is empirically calibrated, its use should yield more meaningful
sample nomograms (see later).
If we then use Gys formulation for the FSE, but using this new formulation for
the liberation factor, we arrive at a General Form of Gys formula (Franois-
Bongaron, 1992, 1993):

R
n
s
f g c d d
M
2 0
3
=

where is a parameter for specific mineralisation which can be experimentally
calibrated. Franois-Bongaron (1996) reports that for most gold ores, 1.5.
Note that = 30 . b .
For any particular sampling step, f, g, c, d
0
, and are constant. Thus, we can group
these terms into a single constant:

R
n
s
K d
M
2
=

where:
K f g c d =

0
3

The new formulation for FSE proposed by Franois-Bongaron helps gain
answers to a number of basic questions, summarised by Assibey-Bonsu (1996,
p.291). In each case we simply alter the unknown in the above formula:
1. What is the weight of sample that should be taken from our lot of ore
(characterised by the constants K and ) if the maximum size of
particles in the lot ( d
n
) is known, in order that the sampling error will
not exceed a specified variance
R
2
? This involves specifying M
s
as the
unknown in our formula.
13

2. What is the possible error introduced when a sample of given weight
M
s
is taken from a lot of ore having a specified value of K and a known
particle top-size of d
n
? This involves specifying

R
2
as the unknown in
our formula.
3. What is the degree of crushing (or grinding) required to lower the error
variance
R
2
to a specified value when we take a sample of mass M
s
,
given the lot of ore is characterised by a constant K ? This involves
specifying d
n
as the unknown in our formula.

13
Equivalently, we could define the problem as one of achieving an acceptable precision.
76

Experi ment al Cali brat i on
Franois-Bongarons re-formulation of Gys equation allows us to avoid
approximation of the liberation factor l. The experimental calibration requires that
we take the logarithms of both sides of Franois-Bongarons equation :

R
n
s
K d
M
2
=

i.e.
( ) ( )
( ) ln ln ln
R s n
M d K
2
= +
The experimental calibration (Franois-Bongaron, 1993, 1996) requires that we
plot ( ) ln
R s
M
2
, which is the left hand side of the above equation, against lnd
n

on log-log graph paper, as shown in figure 2.8:

Figure 2.8 Fitting a model to the FSE (after Franois-Bongaron, 1996)
A straight line of the form y=mx+c can be fitted, where the slope is and the y-
intercept is ln (K). Note also that the model shown accounts for different
behaviour when d
n
< d
0
, (i.e., when we are below liberation size).
In this manner, and K can be calibrated. This means that the formula for FSE is
now suited to the specific ore we are concerned with, rather than the use of a
standard approximation for l by the use of Gys generalised approximation. It thus
tailors the mathematical tool to the problem at hand by capturing more of the
specific character of the lot we must sample.
When we have obtained an experimental value for ln (K), we can easily compute
the liberation size, d
0
since
K f g c d =

0
3

Cal i br at i on
The modified theory is
based on calibration of the
formula for specific
circumstances.
77

and f, g and c are known.
Pract i cal Impl ement at i on
The practical implementation of the calibration experiment is performed by a series
of splitting and assaying at different top-sizes. This experiment is sometimes called
the sample-tree experiment. For details, refer to Franois-Bongaron (1993, 1996).
Sampl e Nomograms
Sample nomograms (or sampling protocol charts) based on the calibrated
constants introduced above can be constructed for a particular ore.
Recall:

R
n
s
K d
M
2
=

Taking logs of both sides:
( ) ( ) ln ln ln

R
s
n
M
K d
2
1
=

+ and
( ) ( ) ( ) ( ) ( )
[ ]
ln ln ln ln
R s n
M d K
2
1 = + +
This last equation shows that for a fixed stage of comminution (meaning a fixed
value of d
n
), the term:
( ) ( )
[ ]
( ) + = ln ln d K =C d
n
constant
and, thus we can simplify:
( ) ( ) ( ) ln ln
R s
M C d
2
= +
78

The above equation is of the form y x c = + , that is, a straight line with a slope
of 1 for a given size d
n
, when plotted on log-log paper.
On a nomogram, the function
R s
M
2
( )is therefore plotted against M
s
on a log-log
scale for each relevant value of size d
n
as shown in figure 2.9. Each time a slope of
1 is obtained.
This means that only one point needs to be found in order to plot the line: if we know
the slope and one point, a straight line is defined. As a result, any sampling operation
at a given stage of comminution (i.e. mass reduction at a constant top particle size
d
n
) can be plotted on the chart as a path along a straight line of slope 1. There is
one such line on a nomogram for each stage of comminution.
On figure 2.9 the line A-B is such a line. The mass corresponding to point A is the
weight of crushed material. The mass corresponding to point B is the weight of the
sample split we take out for the next stage of comminution. The difference
between
R s
M
2
( ) at points A and B represents the segregation free relative
sampling variance for this stage.
Crushing and grinding stages do not contribute to the variance and are therefore
represented by vertical lines on the chart.
The contribution of each stage to the overall sampling variance appears clearly on
the chart. The entire sampling preparation protocol can thus be visualised from the
nomogram. To quote Franois-Bongaron (1996):
Such charts constitute valuable tools for the design, assessment and
control/improvement of sampling processes.
On figure 2.9 a safety line is plotted which corresponds to Gys (1982)
recommendation not to exceed the value of
R s
M
2 2
10 ( ) =

(=10%). Above this
line, the sampling operation incurs an unacceptably skewed distribution of errors.
Thus, above this line, the precision may get out of control and possibly out
of the validity domain of our model (Franois-Bongaron, 1996).

Mass Reduc t i on
It is reduction in mass, not
particle size, that generates
error variances.
79

Figure 2.9 Sampling nomogram (after Franois-Bongaron, 1993). Refer to text for example and
description.
Example Calculat ions for a Sampling Prot ocol
The following example is taken from Franois-Bongaron (1993).
Out of a 10 tonne lot of 1/4 material in a gold mine, a 30kg sample is taken, then
crushed down to minus 28 mesh (= 0.5915mm) to select a final 1kg sample. The
1kg sample is then ground to minus 200 mesh (= 0.074mm). A 300g pulp is then
taken using a laboratory riffle splitter. This pulp is then quartered by hand to select
a 30g grab which is fire assayed. In other words, a 30g sample is taken (in two
stages) out of the 1kg sample at 200 mesh.
Assuming that the FSE model has been fitted to the following formula, which
expresses the FSE as a function of mass:
( )

R s
n
s
M
K d
M
2
=

R
n
s
d
M
2
15
470
=

.

80

This corresponds to = 1.5 and K = 470 g/cm
1.5
and is believed to be acceptable
for free gold ores. A chart can be built to plot the sampling protocol and calculate
the final sample variance (see figure 2.9, above).
On figure 2.9 the various relevant sampling lines (of slope minus 1.0) for the
considered values of d
n
have been plotted by calculating one point per line using
the fitted model introduced above:
R
n
s
d
M
2
15
470
=

.

for arbritrary values of M
s
. The various sampling steps are represented by points
(A) to (G).
The incremental variances can be calculated numerically from the model, but it is
faster and more convenient to read them off the graph. The cumulative relative
variance is calculated as:
[ ] [ ] ( ) [ ] [ ] ( ) [ ] [ ] ( )

R
B A D C G E
2 2 2 2 2 2 2
= + +
Note that, in this case, points (A), (C) and (E) are low enough on the logarithmic
variance scale that their values of the function ( )
R s
M
2
can be neglected, so:
[ ] [ ] [ ]

R
B D G
2 2 2 2
= + +
With:
[ ]
2 3
8 10 B =

,
[ ]
2 3
6 10 D =

and
[ ]
2 3
9 10 G =

(all looked up from the graph).
The exact calculation, using all terms for FSE in our equation returns a cumulated
variance:
[ ] [ ] [ ]

R
B D G
2 2 2 2
3 3 3
3
798 10 580 10 870 10
2248 10
= + +
= + +
=

. . .
.

This corresponds to a relative standard deviation
R
:

R R
= = =
2 3
2248 10 01499 . .
81

Which, expressed in percent, is 15%.
A quick examination of the chart will show that little improvement is possible
within the range of feasible, practical profiles (i.e. little improvement is possible by
increasing the number of intermediary sampling stages). Conversely, it is easy to see
the elimination of the intermediate grinding stage (B-C), i.e. directly taking a 1kg
sample of 1/4 material, will generate a variance increment of 25 10
1
.

, so that
the final relative standard deviation
R
will increase to in excess of 50%.
Finally, assuming a normal distribution for the sampling error, these standard
deviations can be used to construct confidence intervals, but be carefulthe
assumption of normality of the errors is not necessarily true. Therefore the
resultant confidence intervals give only order of magnitude values. If we accept
this assumption, two-relative standard deviations equates to 30% for a 5% risk
(95% C.I.).
Sampling Pract ice for Grade Cont rol
Sampling protocols need to be written & explicit. A sampling protocol must be
clearly documented so that different operators collect the samples in virtually
identical manner. It should include a sample nomogram and prescriptions for
quality control measures (QC).
If they do not already exist in acceptable form, appropriate sampling protocols for
all types of sampling need to be established (in written form) as a matter of urgent
priority as a first step in setting up QC systems for grade control.
Current practices should be assessed before we propose significant changes to the
way samples are collected. The existing procedure should therefore always be
carefully described and documented prior to any changes being made.
Systematic duplicate sampling should be performed for any sampling. We must
institute a program of sample duplication as a matter of priority. At all mines, it
should be a priority to gather a duplicate set of samples (say 100-200 for each type
of sample) as a reference set to establish precision. Many times, this data already
exists and simply needs organisation, analysis and interpretation (see previous
material in this course, above, for statistical techniques for comparing paired
assays).
Once we have the duplicated data, we can set up systematic systems of quality
control (e.g. duplication of every 10th or 15th face underground, or routine
duplicate splitting of RC samples, for example).
Ideally, it is better to perform duplication once we know the original grades,
because it allows us to concentrate our duplication on the critical parts of the
histogram (and avoid the problem of getting most of our random duplicates
telling us the interesting fact that low-grade waste reproduces very well)!
Caut i on
The end result is an order of
magnitude result when
expressed as a confidence
interval.
Doc ument at i on
lack of diocumentation
virtually ensures lack of
consistent approach, and
generally implies poor
practices.
Dupl i c at e
Sampl es
Without duplicate samples,
QA/QC is impossible.
82

If dedicated samplers are employed, we strongly suggest that samplers be closely
involved and informed of what we are doing with QC. This will maximise the
chances of success of introducing new and better sampling culture.
The samplers could be trained to perform simple spreadsheet analysis of this data
on a routine basis to institute quality control. This would give them ownership of
qualitynot only making their jobs more interesting, but helping us get a better
sample by decrease the contribution of operator error to sampling error.

C H 5 S P A T I A L V A R I A T I O N
83

5: Spat ial Variat ion
Nature means the sum of all phenomena, together with the causes which
produce them; including not only all that happens, but all that is capable of
happening.
John Stuart Mill On Nature 1874
Randomness and Orebodies
Since the information we have from our mineralisation is fragmentary, we need a
model to be able to draw any conclusions concerning the unsampled portions of
the mineralisation. As mentioned in previously, this unsampled portion generally
represents almost 100% of the volume considered!
Det ermi ni st i c Approaches
The spatial distribution of metal in orebodies is demonstrably not the result of a
random process
14
. On the contrary, it is controlled by complex combinations of
physical and chemical systems that may include, for example:
Geometry and dynamics of original sedimentary systems.
Petrochemistry and cooling history of igneous rocks.
Geochemistry and thermodynamics of hydrothermal fluids.
Interaction of hydrothermal fluids with rocks.
Localised temperature and pressure gradients.
Structural geology.
Weathering processes.

14
Strictly, we could argue that no natural phenomena at scales above the atomic is random.
Randomness is a creation of the Human mind to cope with a large number of unknown parameters a
formalisation of our ignorance. An excellent discussion of randomness is given by Beltrami (1999).
Chapter
5
84

In each mineral deposit, and often in different parts of the same deposit, the
causative factors (i.e. those controlling metal introduction and deposition) are
different in detail and relative importance.
Since the genesis of mineralisation is a combination of physical processes, the most
intuitively appealing, intellectually satisfactory way to model the spatial distribution
of metal would be to employ a complete physical model of how the grades were
generated. Unfortunately, knowledge of geological processes in such complicated
systems as orebodies can never be sophisticated enough to allow detailed
deterministic models of local ore distribution to be constructed.
Even in the case of relatively simple models of one aspect of a geological system,
deterministic models of physical processes are extremely difficult to construct and
can be very complicated to use. For examples, refer to (Cathles, 1981) and Thorn
(1988) who discuss deterministic modelling of ore mineralisation associated with
cooling igneous intrusions and simple geomorphological and sediment transport
models respectively.
In the case of modelling spatial distribution of grade in an orebody, the numbers of
parameters would be staggering and this approach is clearly a dead end for a miner
or explorationist.
We are now left with the observed data and, usually, some knowledge of the larger
scale factors that influence the distribution of potentially economic grades. For
example, we may be aware of geological structures that offset mineralised bodies,
or be able to distinguish several zones within the orebody that are different in
geological style. On the scale of the samples themselves, however, there is
uncertainty about how the grade behaves between sample locations.
Trend Surfaces
We may try to apply a well-known statistical method, such as trend surface analysis.
The implicit assumption underlying these types of regression methods is that the
surface under consideration can be represented (at least locally) by a fairly simple
deterministic functionsuch as a polynomialplus a random error component.
Here random means that the error is uncorrelated from one place to another, and
is also uncorrelated with the function.
The trend surface approach was applied to the problem of modelling geological
spatial data by Gomez and Hazen (1970) to model the proportion of pyritic
sulphur distribution in a coal seam (see Table 5.1).

Det er mi ni st i c
Model s
Are impractical and
effectively impossible to
construct and use.
What do w e have?
Sample data (complete with
associated error) and a gross
understanding of geology or
zonation of the deposit.
85

Table 5.1 Appendix A from Gomez and Hazen (1970)see text for discussion
The problem with such an approach is that most geological variables (and certainly
all economic grade variables) exhibit considerable short-scale variation in addition to
the larger scale trends that can be reasonably described by a deterministic function
like that in table 5.1.
In this trend surface approach, we are constrained by insisting that we have
uncorrelated errors. This means that the function we employ must twist and turn a
lot, and this explains the profusion of exponential and trigonometric terms in table
5.1! This suggests that we might be better off to allow correlations between values
at different distances apartand this is the basic idea of geostatistics.
Probabil i st i c model s
Geologists who have performed detailed sampling studies know that geological
variables (grade, thickness etc.) tend to exhibit considerable short-scale scatter. Their
spatial variations are so complex that they are not amenable to a representation in
terms of ordinary mathematical functions. If we could know the real distribution of
Shor t -Sc al e
Short-scale scatter is a
fundamental feature of grade
data.
86

grades along a traverse and plot them, the trace might look like figure 5.1: spiky
with seemingly unpredictable jumps and a saw-toothing pattern to it. Contrary to
the over-optimistic view of trend surface approaches, it seems no interpolation is
possible at all.
The partial knowledge of factors influencing spatial distribution of grade thus
mitigates against using deterministic models for the detailed distribution of
mineralisation. This is our motive for adopting Probabilistic models when dealing with
ore deposits.
Randomness
Using a probabilistic model allows us to incorporate this uncertainty by viewing the
available data as the outcomes of a random process. Adopting a probabilistic approach
to modelling mineralisation does not imply any belief that the underlying process is
random. Our understanding of the numerous and complex physical processes
forming ore, especially in the light of volumetrically insignificant amounts of
sampling, is generally so poor that this complexity can only be captured
satisfactorily by a probabilistic model.

Figure 5.1 Random & structured aspects of an regionalised variable or ReV
The colloquial use of the term random as a synonym of unpredictable is inappropriate
in this context. Although tossing of coins and dice are typical of situations that can
Random?
Use of a probabilistic model
does not imply randomness
of the subject data!
87

be modelled successfully by the approach of random variables they are in fact entirely
suited to the application of deterministic models: if we have a sufficient knowledge of the
variable factors involved.
Coi ns and Di ce
The result of tossing a coin is controlled by simple Newtonian physics. However,
the changes in initial conditions and dynamics involved in a given toss (exact initial
position, details of forces applied, local air current and temperature fluctuations
etc.) are sufficient to change the result. In consequence, the result appears to be
random, and we may treat the result of any given throw as the outcome or
realisation of a random variable (RV).
We cannot predict the outcome of a given toss of a die or coin. The results are,
however, predictable in the sense that we can state the probability for the coin
lands with heads facing up or throwing the die results in an even number showing
on the uppermost face for any given trial.
Investigation of dice, coins and drawing ping-pong balls from a bag form much of
the traditional content of introductory courses in statistics and probability because
the probabilities are easily obtained.
For a fair die, each elementary outcome occurs with equal frequency in the long
runin fact, this forms one definition of probability (Feller, 1968). If the die is
biased (loaded) then we may choose other probabilities after observing a large
number of trials (tosses). This approach is plainly unavailable to us with orebodies!
The Geost at ist ical Approach
In geostatistics we generally cannot observe numerous outcomes of the process
being studied. We have a set of spatially distributed data (the grades of samples, for
example), obtained from a unique orebody, and we wish to characterise the
random process that could produce the data we observed. So, although the idea of a
probabilistic model seems a good direction to pursue, we need to consider a few
factors in more detail.
Most of the time, if we had access to a plot like that in figure 5.1, closer inspection
would reveal that the grades are not completely random. We expect this, given our
knowledge of the gross geological and genetic factors behind ore deposits. We see
that samples close to each other on our traverse seem to be correlated, i.e.
neighbouring points appear to be related: on the whole, there are zones where
values tend to be high and lower-grade zones.
In real mineralisation we expect some spatial pattern of grades, preferred
orientations for high-grade zones, evenly mineralised areas and more randomly
mineralised zones.

Fr equenc y
Def i ni t i on
We cannot repeat the
orebody to obtain
probabilities!
Spat i al
Cor r el at i on
Spatial correlation (or lack of
it in degrees) is the key
feature of most mining data
sets.
88

The Dual Aspect s of Regi onali sed Vari abl es
The term Regionalised Variable (ReV) was coined by George Matheron to emphase
the dual nature of such variables, which combine two different aspects:
1. A random aspect: that accounts for local, small-scale irregularities.
2. A structured or regionalised aspect: that accounts for the large-scale
tendencies of the phenomena.
The common statistical models (like trend surfaces) put all the random component
into an error term while all the structured component is accommodated in a
deterministic function. This is not realistic for geological phenomena.
A better way of representing the spatial distribution of grades is to introduce the
randomness in terms of fluctuations about a fixed surface that geostatisticians refer
to as drift (to avoid any possible confusion with the term trend used in the
previously described trend surface approach). Fluctuations are thus not considered
as errors but rather as fully-fledged features of the phenomenon under
consideration, i.e. features of the spatial distribution of grades.
The first task in geostatistics is to identify these random and regionalised structures,
referred to as structural properties. The process of identifying and modelling these is
structural analysis. After this step, we can progress to solving various types of
problems, including estimation.
Regionalised Variables: Concept ual Background
Random Funct i ons
The observed value at each data point x can be considered as the outcome z(x) of a
random variable (RV) Z(x). Figure 5.2 illustrates the relationship involved. The
mean of the RV Z(x) at the point x is called the drift m(x).
At locations in space where no samples are available, the values of z(x) are well
defined, even though they are unknown. The values of z(x) at these locations may
be viewed as outcomes of random variables Z(x). In mathematical terminology, the
family of all such RV's, Z(x) is called a Random Function (RF)
15
.
A random function bears the same relationship to one of its realisations as a
random variable does to its outcome. Note that the realisation of an RF is a
function, whereas the outcome of an RV is a number. A random function is
characterised by the joint distribution of a set of random variables, i.e.
k k
x x x x Z x Z x Z K K , , points all for ) ( ), ( ), (
2 1 2 1

15
Synonyms for RF include stochastic process and random field.
Noi se
The random or chaotic
component of grade
variability cannot be ignored
if we are to have efficient
estimation.
89

For our probabilistic model to be useful we need to make some assumptions about
the characteristics of these distributions. Specifically, as discussed earlier, we only
have one realisation available (in general). This is a general problem of statistical
inference: when only a single realisation is available we require further assumptions.
These additional assumptions, or hypotheses, reduce the number of parameters upon
which the RF depends.
The whole point is to introduce the minimum number of hypotheses to enable our
model to cover the widest range of practical situations.
Note that no estimation methodology is devoid of assumptions, and that some of
the assumptions behind classical methodologies are really very strong. For
example, in a polygonal estimate, we assume that the grade is constant over the area
of influence defined by a polygon!

Figure 5.2 Summary of Concepts (Random Variables & Random Functions)
St r ong or Weak ?
In science and mathematics,
weaker hypotheses are
usually preferred because
they admit more general
cases.
90

St at ionarit y
It is common is many statistical applications to assume that a variable can be
considered as being stationary. In other words, that the distributional law of the
variable is invariant (does not change) under translation. A stationary random
function is homogeneous and self-repeating in space. The assumption of
stationarity makes statistical inference possible.
St ri ct St at i onari t y
In its strictest sense, stationarity requires all the moments of the distribution to be
invariant under translation, i.e. exactly the same distribution at every point in the
field considered. This cannot be verified from the limited sampling usually
available. In any case, such a strong assumption is not necessary to enable statistical
inference in geostatistical applications.
Weak or 2nd Order St at i onarit y
In geostatistics we usually require only that the first two moments of the
distributionthe mean and the covariancebe invariant under translation (i.e.
constant). This is called weak or second order stationarity For this hypothesis we
assume:
1. That the expected value (or mean) of the RF Z(x) is constant for all
points x, i.e.
E Z x m x m ( ) ( ) = =
for any x.
2. That the covariance function C(h) between any two points x and
(x+h), where (x+h) is separated from x by a vector distance h, is
independent of the location of the points x and (x+h). This is
expressed mathematically as:
E Z x Z x h m C h ( ) ( ) ( ) + =
2

In other words the covariance between any two points depends only on the
distance and direction between the two points, not on the specific locations of the
points themselves.
In particular, when h=0 the covariance comes back to the ordinary variance of
Z(x), which must also be constant under the assumptions of weak stationarity.
The Int ri nsi c Hypot hesi s
In practice, it is often the case that the assumptions of weak stationarity are not
satisfied. Clearly, when there is a marked trend in the mean (for example a
pronounced and systematic increase in grades towards the core of a mineral
deposit) the mean value cannot be considered constant, so assumption (1) above
will not be valid. Likewise, there are situations where definition of a constant
Lot t er i es
The probability of getting a
particular number in a
lottery
I nt r i nsi c
Hypot hesi s
This is the practical
definition for stationarity
used in mining geostatistics.
91

covariance is problematic. Refer to Journel and Huijbregts (1978) for a more
expanded discussion.
So, on both theoretical and practical grounds it is convenient to be able to further
weaken our stationarity hypothesis.
Under the intrinsic hypothesis we suppose that the increments of the function are
weakly stationary. This means that the mean and variance of the increments, i.e.
Z x h Z x ( ) ( ) +
are independent of the specific location of the point x.
The intrinsic hypothesis can be summarised:
E Z x h Z x
Var Z x h Z x h
( ) ( )
( ) ( ) ( )
+ =
+ =
0
2

This is the intrinsic hypothesis with zero mean increment.
Using the intrinsic hypothesis means that we have decided that it is appropriate to
pool sample pairs, separated by (approximately) the same distance vector, in the
domain of interest.
The function ( ) h is called the semi-variogram (we usually say the variogram for
short). The variogram is the basic tool of geostatistical structural analysis and it is
employed for subsequent estimation. Given its importance to geostatistics, we will
consider the variogram in some detail in this and the next chapter. However,
before we continue, we will first discuss the practical aspects of stationarity a little
further.
The St at i onarit y Deci si on
It is important to understand that stationarity is a property of the model, not of the
phenomena we are considering. Furthermore, the correctness of the decision to
assume stationarity in our model cannot be refuted or proven a priori. The decision
of stationarity is a decision we make based on all the information at hand, for
example:
Geological zonation.
Weathering domains
Statistical characteristics (especially variability)
Spatial variation (as characterised by the variogram or equivalent)
Assumptions about zones of homogeneous mineralisation, etc.
92

The decision of stationarity is thus an expert decision based on a piori assumptions
about the homogeneity of the zones over which averaging is to take place (Journel,
1987).
Note also that in practical estimations, the variogram is only used up to a certain
distance. This limit is generally the diameter of the search neighbourhood to be
used in kriging. Consequently, stationarity need only apply to separations up to this
distance: the further limitation of the stationarity hypothesis to distances less than
this is called the hypothesis of quasi-stationarity.
Accepting the assumption of quasi-stationarity means that we can consider a series
of sliding neighbourhoods within which stationarity applies. As such the decision
of quasi-stationarity is scale-dependent.
The Variogram
The fundamental basis of most geostatistics is the variogram. The variogram is the
basic diagnostic tool for spatially characterising a regionalised variable and is also
central to geostatistical estimation or interpolation methods (kriging) and the more
advanced methods of conditional simulation.
Defi ni t i on of t he Vari ogram
The variogram of an intrinsic random function is defined as:
( ) ( ) ( ) [ ] h Var Z x h Z x = +
1
2

Because we have assumed in the hypothesis of intrinsic stationarity that the mean
drift is zero:
( ) ( )
[ ] E Z x h Z x + = 0
then the variogram is equal to the mean square value of the difference:
( ) ( ) Z x h Z x +
i.e. the variogram can be defined as:
( ) ( ) ( ) { }
[ ]
h E Z x h Z x = +
1
2
2

In practice, the following formula is used to compute the experimental variogram from
the available data:
( ) ( ) ( ) { }
[ ]
$
h
N
Z x h Z x
i i
i
N
= +
=
1
2
2
1

The Var i ogr am
In all situations, the
important part of the
variogram is for short
separation distances.
93

The experimental variogram is calculated using N data pairs. The x and x+h refer
to data points with spatial locations. The locations x and x+h are in n-dimensional
space, i.e. may refer to n=1, 2 or 3 dimensions in mining applications. For example,
in a two dimensional situation n=2, the coordinates of x and x+h would be {x
1
,x
2
}
etc. Consequently, the separation h is a vector in 2D with components h
1
and h
2
. In
two dimensions, the variogram is therefore a function of the two variables h
1
and
h
2
and the variogram can model anisotropic phenomena.
Mai n Feat ures of t he Vari ogram
The graph of ( ) h when plotted against h usually presents the following features
(figure 5.3):
( ) h is a non-negative function, i.e. ( ) h 0
It starts at 0 for h=0.
It generally increases with h.
( ) h may rise up to a certain value of h (called the sill) then flatten out, i.e.
stabilise.
Alternatively, ( ) h may continue to rise for increasing lags h.
Figure 5.3 summarises most of the different aspects of the variogram that are
important from the point of view of structural analysis. We will consider some of
these next.
Range and Zone of Infl uence
The rate of increase of the variogram with increasing h is indicative of how rapidly
the influence of a sample decreases with distance. In fact, ( ) h gives a precise
meaning to the traditional concept of zone of influence of a value.
At separations less than the distance at which the variogram reaches its limiting
value (the sill) samples exhibit some degree of spatial correlation. Beyond this
distance, samples are not spatially correlated (i.e. they are spatially uncorrelated). The
separation at which there is a transition from spatial correlation to lack of
correlation is called the range. The range is usually denoted by the letter a in
geostatistics.
Variograms that possess a range are described as transitional variograms, transitive
variograms or bounded variograms. The phenomena such variograms describe are
sometimes called transitive phenomena.
Not all variograms reach a sill, and thus not all variograms can be said to have a
range. Such variograms are non-transitional or unbounded.

Spat i al
Cor r el at i on
The variogram is a measure
of spatial correlation.
94

Figure 5.3 Main features of the variogram

Figure 5.4 shows the contrast between transitional and non-transitional variograms.

Figure 5.4 Bounded and unbounded or transitional vs. non-transitional variograms
95

In theory, the limiting value of ( ) h is equal to the variance of the population of
samples used. In fact, when the correlation between Z(x) and Z(x+h) vanishes, we
can write:
( ) ( ) ( ) [ ]
( ) [ ] ( ) [ ] { }
( ) [ ]
h Var Z x h Z x
Var Z x h Var Z x
Var Z x
= +
= + +
=
= =
1
2
1
2
1
2
2
2
2
2
2

Defining the variogram as half the mean square difference ensures the above
equivalence with the variance.
When the variogram is bounded, it is related to the covariance function by:
( ) ( ) ( ) h C C h = 0
Note also that the range need not be the same for all directions considered. This
aspect of the range is anisotropy, which we consider separately, below.
There may be more than one range in a given direction. In this case we have nested
structures (or intermeshed structures) that reflect distinct spatial correlations acting
over different scales. Again, we consider this in more detail, below.
Behavi our Near t he Ori gi n
The behaviour of the variogram near the origin, i.e. for very small lags, mirrors the
regularity and continuity of the regionalised variable itself. Different types of
behaviour are summarised in figure 5.5 and discussed here.

Figure 5.5 Behaviour of the variogram near the origin
96

HI GHL Y CONTI NUOUS B EHAVI OUR ( EXTR EME CONT I NUI TY )
Parabolic behaviour near the origin is characteristic of extremely continuous short-
range regularity. A physical example might be for the variable the elevation of a
very gently undulating, smooth topographic surface. In this case we expect values
close together to be, on average, very similar (virtually the same), hence the parabolic
shape.
Variograms of this type for grade variables in mining applications are so rare as to
be virtually non-existent. Even more regular mining variables such as the thickness
of a vein do not result in such continuous short-range behaviour.
Note that parabolic behaviour near the origin can also be associated with the
presence of a drift (see further, below).
MODER AT EL Y CONT I NUOUS B EHAVI OUR
Linear behaviour of ( ) h near the origin is indicative of moderate short-scale
continuity. The continuity is markedly less than for parabolic behaviour. Some base
metal deposits exhibit this type of variogram, although often accompanied by nugget
effect.
DI S CONT I NUOUS B EHAVI OUR
This is where ( ) h does not tend to zero as h tends to zero. Discontinuous
behaviour near the origin reflects a highly irregular behaviour of the regionalised
variable at short distances. Most geological variables, especially grades, exhibit this
type of behaviour.
The classic example of this is the behaviour of gold assays at short distances due to
the physical distribution of Au in nuggets, as noted by gold geologists for many
years. Consequently, the term nugget effect has been applied to describe this abrupt
jump at the origin.
In the gold example, the grade passes abruptly from high to low values due to the
presence or absence of physical nuggets of Au. This phenomenon can be apparent
at scales as small as the diameter of a core, as geologists assaying two halves of a
split core from a gold deposit will know!
Less radicalbut still quite discontinuousbehaviour at short ranges can be
manifested by mineralisation where physical nuggets are not so apparent. Examples
include hydrothermal tin deposits and many types of uranium mineralisation. The
presence of microfaulting, etc. may also result in an abrupt discontinuity at the
origin.
The apparent nugget effect is sensitive to the spacing of sampling, and reduced
sample spacing may resolve a short range structure and thus decrease the observed
nugget effect.
Ex t r eme
Cont i nui t y
This is not seen for grade
variables, in practice, with
the possible exception of very
long drill hole composites
(where the variability is
smoothed out by the
compositing process)
Nugget Ef f ec t
There is no necessity for
physical nuggets to be
present in order to have a
nugget effect. In fact,
mineralisation with no
appreciable nugget effect is
the exception, rather than
the rule.
97

It is convenient (and conventional) to apply the term nugget to short range
discontinuous behaviour of ( ) h even when it is known to be due to some other
factor. For example, sampling or mismeasurement errors, locational errors and
unresolved microstructures may all be responsible for "nugget effect".
R ANDOM B EHAVI OUR
The flat ( ) h plot represents extreme discontinuity of the regionalised variable. It
equates to complete randomness, chaotic behaviour of values or white noise. In
this case there is a 100% nugget effect and no perceptible correlation at any of the
lags used to construct the variogram. This type of variogram is sometimes called
pure nugget effect.
In the case of such a flat variogram, the regionalised variables Z(x) and Z(x+h) are
uncorrelated for all values of h, no matter how close. This is the limiting case of
total lack of regionalised structure. Note that, once again, this type of behaviour is
highly sensitive to sample spacing, and also sensitive to sampling quality..
Ani sot ropy
Anisotropy is present when there are differences in behaviour of the variogram when
it is calculated in different directions. For example, we may calculate the
experimental variogram in the direction North-South and also for East-West.
Substantially different shape for the two resultant variograms indicates anisotropy.
The absence of anisotropy results in variograms being basically the same shape,
regardless of the direction of calculation. In this case the variogram depends only
upon the magnitude of the distance separating the samples at x and x+h, i.e. |h|.
Such behaviour is referred to as isotropic.
There are two different types of anisotropy (see figure 5.6):
Geomet ri c Ani sot ropy
Geometric anisotropy is also sometimes called elliptical anisotropy and it can be
corrected by a simple linear transformation of the coordinates. In other words, if
the variogram in one direction can be transformed to that in any other just by
changing the scale on the abscissa (the h-axis), then we have a geometric
anisotropy. Such a simple, linear, geometric "stretching" transform is called an affine
transformation.
Note that, in the case of a geometric anisotropy, for a transitional variogram, the
sills of the variograms in each direction are the same. Only the range is different. In
the case of a linear variogram it is the slope that is directionally dependent.

Pur e Nugget
When 100% of the
variability is nugget, i.e.
random, we should check
for sampling problems.
98

Figure 5.6 Geometric anisotropy for bounded and unbounded cases

We can plot the range (or slope, in the case of a linear variogram) as a function of
the direction (figure 5.6). For geometric anisotropy, the plot will approximate an
ellipse (in 2D, an ellipsoid in 3D); a simple change of coordinates transforms this
ellipse into a circle, eliminating the anisotropy.
Note that, when calculating the experimental variogram it is important to choose at
least four directions. This is because choosing only two may not detect a geometric
anisotropy, even if one is present (see figure 5.7).

Figure 5.7 Perception of anisotropy can be artificially influenced by the grid geometry if we choose too few
directions for variogram calculation.
Zonal Ani sot ropy
More complicated types of anisotropy exist in some deposits. An example is the
case where distinct zonation of high and low values exist (for example the presence
of pay streaks, or a control on mineralisation that is sub-parallel to the hanging
99

wall or footwall of the deposit). In this case the variability in the direction parallel to
the direction of zonation might be significantly lower than in the direction
perpendicular to zonation. Figure 5.3 illustrated this concept. This type of
anisotropy is called zonal anisotropy.
Another common example of zonal anisotropy is in the case of stratified deposits
(e.g. iron, coal, lateritic nickel etc.) where the variation in the vertical (or more
generally, orthogonally to the strata surfaces) is higher than that along the strata.
For this reason, zonal anisotropy is sometimes, although less commonly, referred
to as stratified anisotropy.

Figure 5.8 Summary of the concepts of anisotropy and zone of influence.
Presence of a Dri ft
Theory shows that for large values of h, ( ) h must increase more slowly than a
parabola. More specifically,
( ) h
h
h
2
0 as
In practice, we see variograms that increase more rapidly than h
2
. This is an
indication of the presence of a drift. Figure 5.9 shows an example of this.
The experimental variogram we calculate:
( ) ( ) ( ) { }
[ ]
$
h
N
Z x h Z x
i i
i
N
= +
=
1
2
2
1

gives us an estimate of the raw variogram:
( ) ( ) ( ) { }
[ ]
h E Z x h Z x = +
1
2
2

100

( ) ( ) { }
[ ]
( ) ( ) [ ] ( ) ( ) { } [ ] E Z x h Z x Var Z x h Z x E Z x h Z x + = + + +
2 2
(mean square) (variance) (bias)
2

So, it follows that:
( ) ( ) ( ) { }
[ ]
( ) [ ]
h E Z x h Z x
h m x h m x
raw
underlying
= +
= + +
1
2
2
2
( ) ( )

This shows that when there is a drift (i.e. the mean of the increments is not equal to
zero) the experimental or empirical variogram ( ) $
h , which estimates the raw
variogram, is always an upwardly biased estimator of the true or underlying
variogram.
Because of this squared bias term, in the case of a linear drift, it turns out that the
quadratic term 05
2 2
. a h (a parabola) is added to the underlying variogram:
( ) ( ) h h a h
raw underlying
= +
2 2

Figure 5.9 Raw and underlying variogram (linear drift)

101

The raw variogram only coincides with the true or underlying variogram if the
increments have zero mean, otherwise:
For small values of h (i.e. short distances) the effect of this term is quite small, but
for longer distances, it may become the dominant term in the raw variogram, and
so we see rapid growth of the experimental variogram.
Drifts are not necessarily linear. Non-linear drift is more complicated and harder to
take into account. This is because the bias term m(x+h)-m(x) now depends not only
on h, but also on x, as does the raw variogram since the increments are no longer
stationary.
Proport i onal Effect
A proportional effect exists when there is a relationship between the local mean and the
corresponding local variance. The usual test for proportional effect is to consider
the data in approximately equal groupings and calculate the mean and variance for
each cell.
In a mineral deposit, for example, we might cut the deposit up into squares or
strips, use moving windows or choose individual drill holes as the grouping unit. It
is important that these groups are of approximately equal size, shape and contain,
on average, about the same number of samples. The number of samples in each
one should be large enough to estimate the mean and variance (say, more than 20).
We plot the squared mean against the variance (or equivalently, the mean against
the standard deviation). If a relationship is evident, we say there is a proportional
effect.
A proportional effect is generally present for lognormally distributed values, and
often present for other skewed distributions, for example in gold deposits.
A variogram is said to have a proportional effect when the value of ( ) h is
proportional to the local mean grade. In this case, the variogram of different zones
have the same shape, but different sills. The sill of the variograms calculated in rich
zones will be higher than for those in poorer zones.
It often turns out that the sill is proportional to the square of the local mean. The
underlying variogram in this case can be found by dividing the local variograms by
the square of the local mean and then averaging them before fitting a model (this is
considered in more detail later).
Nest ed St ruct ures
Nested structures or intermeshed structures indicate the presence of spatial correlation at
different scales. These different scales of variation are superimposed. Figure 5.10
illustrates a variogram with clearly nested structures.

Pr opor t i onal
Ef f ec t
Skewed distributions imply
proportional effect.
102

Figure 5.10 Nested structures, periodicity and hole effect
For example, we may have three distinct scales of variation in a regionalisation:
For very short scales ( ) h 0 , or strictly, at distances less than the
minimum sampling lag, there is a nugget effect (discussed previously).
At relatively short ranges, up to several lags, there may be a short-range
spatial structure than reflects distribution of mineralisation in "pods" or
other clustering of higher grades. This results in a distinct structure with a
range equivalent to the average pod dimension in the direction of
variogram calculation.
At longer distances there may be a structure with a range determined by
the overall dimensions of the mineralised zone. This structure is related to
samples passing from ore into waste, i.e. the range is related to the average
maximum distance between sample pairs within the ore zone.
Hole Effect
In some cases, we observe a bump in the variogram. This would correspond to a
hole in the covariance, hence the name hole effect. Figure 5.10 shows an example.
In many cases, an apparent hole effect is the result of lack of samples for given lags
or other perturbations or fluctuations of the experimental variogram (which is, as
we have pointed out, an estimate of the "true" variogram). In most cases, apparent
hole effects can, and should be ignored unless there is a sound physical explanation
at hand.
The classical example of a hole effect with a good physical explanation is that of
Serra's early study of thin sections of oolitic iron ore from a French iron deposit. In
this case, Serra found that calcite crystals tended to be separated by intervals
roughly proportional to their size, presumably because of the deposition of calcite
around randomly located germs (or seeds).
Other examples do exist, where there is a physically explicable hole effect. Hohn
(1988) cites the case of a hole effect for variograms of the top of a folded
sedimentary surface. We also see hole effects caused by pronounced periodic
banding of grades. David (1977) gives the example of the Prince Lyell orebody at
Queenstown in Tasmania, where the ore is in a series of distinct high grade lenses,
separated by low grade material and a pronounced hole effect was observed.
Hol e Ef f ec t
Anisotropic hole effects are
often associated with zonal
anisotropy.
103

Journel and Friodevaux (1982) present a modelling approach for anisotropic hole
effect.
However, true hole effects are not really very common in practice, and one should
be wary of apparent hole effects.
Peri odici t y
If hole effects are relatively rare, then true periodicity is virtually unheard of. In
theory, a very regularly spaced intercalation of high and low grade zones of very
similar width might result in a periodic variogram.
It is so difficult to find geological variables that meet these criteria of highly regular
intercalation that observed periodicity must be generally regarded as a statistical
artefact caused, for example by inclusion and exclusion of extreme values in certain
lags.
It should be noted that some non-mining examples could certainly generate
truly periodic variograms, e.g. time domain data (temperatures, prices) might be
expected to be periodic.

C H 7 S U P P O R T
104

6: Variography
The proper conclusions of an analysis of spatial variability will only be
reached if there is close contact with the geologist or, better still, if the analysis
is carried out by the geologist himself the best mining geostatistician is the
one who is able to combine his geological knowledge and his technical mining
skill with a good use of the probabilistic language.
Andre Journel & Charles Huijbregts Mining Geostatistics 1978
The Science and Art of Variography
Variography is the calculating of experimental variograms and subsequent fitting of
appropriate variogram models. The process of determining an acceptable and
coherent model for spatial correlation is also referred to as structural modelling.
The general principles of variogram modelling will be looked at in some detail here,
and we will conclude this chapter with a case study.
The Ai ms of St ruct ural Anal ysi s
The end-result of structural analysis is a coherent model for spatial variability. This
model may then be used for several different purposes:
1. To characterise the spatial variability of the mineralisation as part of an
integrated geological study.
2. To enable change of support to be modelledrequired for global
recoverable resource estimation (see Chapter 7).
3. To provide the basis of estimation variance studies or assessment of
sampling spacing (see Chapter 8).
4. To obtain a weighting function to be used in optimal local
estimationkriging (see Chapter 9).
5. To use as a structural function for simulation of deposits (see Chapter
12).
Chapter
6
C H 6 V A R I O G R A P H Y
105

In each case we wish to fit the experimental variogram with a model that captures
the main features of spatial variability that are important for the application we
have in mind. We will discover that not all features of the variogram have equal
importance, depending on the use to which we put our variogram model.
How we model the variogram has serious implications when estimating or
simulating. Consequently, the task of calculating and estimating variograms is
central to the practical application of geostatistics.
Pract i cal Aspect s of a St ruct ural Anal ysi s
Structural analysis forms the foundation of any geostatistical study, whether for
grade characterisation, estimation, simulation etc. We are interested in
characterising the regionalisation and also in obtaining a mathematically admissible
model for the variogram.
Prel i mi nary St eps
Prior to getting going with the structural analysis, there are a few essential
preliminaries. In fact many of these are not specific to the geostatistical approach
and just constitute good practice for resource estimation.
DAT A VAL I DAT I ON
The importance of checking and validating data simply cannot be overstated.
Errors that are of dangerous magnitude can be introduced by the most trivial data
entry errors: for example, reversing the northing and easting of the collar
coordinates could put your richest hole on the wrong section.
While you might expect that this point need not be laboured with industry
professionals, some geologists tend to trust the data collection end of
computerised resource assessment too much. The job of checking data is tedious,
but it can be integrated with the general (and necessary) process of interpretation
and getting a feel for the data.
The very first step is to assess data quality. Initially, we will need to know how
samples were collected (intervals, splitting, sample mass, preparation and assay
methodology). Often, we cannot change these at this late stage, but if the sampling
precision looks poor, it is important to know this. We also need to clearly know if
several types of sampling have been undertaken, and if so, which holes were
sampled by which methods.
GET T I NG A F E EL
F OR T HE DATA
A general process is outlined as an aid to this part of a resource estimation study is
summarised below:
Duplicate data and assay replicates should be statistically assessed. At the
very least, generate XY plots to look for any systematic biases.
I mpor t ant
Understanding variography
is the key to understanding
geostatistics
Dat a Qual i t y
Variography is sensitive to
poor data.
106

Generate plots of drill holes that show the assays as both numbers and as
histograms. As a minimum, generate cross-sections and strategically placed
level plans. If possible, work with comprehensive sets of cross-sections,
longitudinal-sections and level plans. On both sections and level plans, plot
the topographic surface at the time of drilling to check for errors in collar
RL.
Look for the very high values and try to assign them a geological context.
Always check the 20 or 30 highest assays against the geological logs and
original assay sheets. These highest values (especially in a gold deposit) will
contribute much of the metal and thus impact disproportionately on the
variography and subsequent estimation. In some cases (eg. Fe in an iron
deposit) very low values can have a similar impact. The possibility of data
error (i.e. the assay value is incorrect) or locational error (the assay is valid,
but not in the right place) must be precluded. If you cannot check every
assay, at least check the assays that will have most impact on the estimate.
If you are unfamiliar with the data collection phase for the deposit you are
working on, it is helpful to make a plot of collar coordinates with drilling
dates (if available in the database). This may show up holes "drilled" out of
sequence and may point to possible locational errors.
Check surveys on holes that seem to have excessive or "strange"
deviations.
Look for obviously unsampled intervals and try to find out why. If intervals
of potential mineralisation are unsampled, it may be necessary to return to
cores or sample rejects.
If areas are undrilled, or holes are terminated in mineralisation, try to
establish why.
107

The aim at this stage is to get an overall view of the data in context with both
geology and the problem at hand: resource estimation. Some time invested at this
stage can avoid the drastic step of having to re-do the entire study if serious data
errors are revealed late in the estimation process.
This whole process runs in parallel with validation of the geological model. Some
of this might be done by using computer graphics on screens, but the bulk of it is
best performed with hard copy from the plotter!
The quality of a geostatistical (or other resource evaluation) study depends to a very
large degree upon having a good feel for the data. The only way to get a good feel
is to spend sufficient time becoming familiar with sections and plans.
If the person responsible for resource estimation is not the project geologist, then
time needs to be spent talking to the geologists to get an appreciation of the
important features of the deposit and the exploration logic, for example:
If some areas are preferentially sampled, why?
Do particular features or lithologies appear to be spatially associated with
mineralisation?
Does the geologist have a feel for zones that might be considered as
stationary when calculating the variogram?
Geological ideas about grade distribution can sometimes be confirmed by
variography. Because variography reflects the actual spatial distribution of grades, it
can be a powerful exploratory tool for the geologist. The integration of geology and
geostatistics enhances both aspects of the study.
C L AS S I C AL S T AT I S T I CS
One of the basic assumptions in most geostatistics is that the data come from a
homogeneous population. Of course, few ore bodies are completely homogeneous.
Usually, different zones will need to be defined (this is the issue of stationarity,
dealt with before). It is therefore important to calculate a few simple statistics
before continuing to the step of variography.
The most important statistics to calculate are:
The mean.
The variance and standard deviation.
The coefficient of variation, or relative standard deviation.
The histogram.
Correlations between pairs of variables if the problem is multivariate.
Geol ogy
The role of the geologist is
critical. If the geostatistician
is not a geologist, time needs
to be spent to ensure they
are quite familiar with
important aspects of the
geology of the deposit.
108

We should always report the number of data used for our analysis.
An important aspect of what we are looking for when we examine these statistics
and plots is the presence and significance of extreme values: values that have a
substantial impact on variography and subsequently, the estimate.
When looking at histograms check to see if there is more than one mode. The
mode is defined as the most frequently occuring value. Bimodal, or multimodal
histograms may indicate several different populations are being mixed: we must
separate these if possible.
If you have any intention of using lognormal-based methods, then a plot of the
histogram on log-probability paper is mandatory. Such methods are often highly
sensitive to deviations from lognormality, so care should be exercised.
Look for very high values. A rank listing of the 20 or 30 highest values can often be
generated with modern software, allowing us to locate their coordinates on sections
or plans very quickly.
Plotting to check for the presence of the proportional effect is also advisable. If
you do not have software to calculate moving window statistics, then divide the
deposit up into fixed blocks, each with more than 20 samples, and see whether a
plot of the block mean versus the block standard deviation shows any correlation.
Note that a proportional effect is implicit for lognormal data. We discuss the
implications of this later.
If we are making stationarity decisionsfor example, separating (or combining)
two geological zones for the purposes of variographythen it's important to look
at the statistical characteristics of each zone. In addition, it is important that we do
not include unmineralised materials at the margins of our zones. Note that most
modern drill hole databases include all the data (including many intervals outside
the area of immediate interest) so this is an important point.
In summary:
1. We want to locate drastic errors.
2. Drastic errors are those that will materially impact upon the estimates.
3. There is no substitute for looking at plots. In addition to 3D
visualisation, our experience shows that careful consideration of
printed sections and plans is necessary.
4. There is no excuse for not being familiar with the geology. Everything
should be done in context with the geology.
5. A few days of data checking is trivial compared to re-doing the
estimate, not to mention the possibility of economically catastrophic
error.
Ex t r eme Val ues
The highest grades in
positively skewed
distributions have a big
impact. We must check
them carefully and
understand their
distribution.
109

How t o Comput e a Variogram
We consider here the practice of calculating the experimental variogram:
( ) ( ) ( ) { }
[ ]
$
h
N
Z x h Z x
i i
i
N
= +
=
1
2
2
1

which is an estimate of the raw variogram, as presented in the previous chapter:
( ) ( ) ( ) { }
[ ]
h E Z x h Z x = +
1
2
2

Since the variogram can be defined for = 1, 2 or 3 dimensions, the experimental
variogram can be calculated in 1, 2 or 3 dimensions. First, we should note that
variograms should, strictly, be calculated only on samples of equal support. This will
often involve compositing the data to equal lengths. Note that, as a rule, the length
we composite to should never be less than the average sample length, and in most
open-pit cases, should generally be the length corresponding to the intended
vertical selectivity (i.e. flitch height).
If we have two quite different drilling campaigns, we must determine whether they
can legitimately be considered equivalent orand in most instances this will be the
caseseparate the data from the two campaigns. Similar considerations may apply
to assay flow-sheets.
1-D: Al ong a Li ne
Sometimes we wish to calculate a variogram along a line, for example, the
calculation of the experimental variogram of samples along a drill hole can be
conveniently considered as being in one dimension. Other examples include the
variogram of seismic times along a profile, chip samples along a mining face or the
variogram along Ditch Witch grade control samples.
For calculations, we can consider the samples to be located at the centre of each
sample interval. If the points are regularly spaced along the line, the variogram can
be computed for each lag h using the formula:
( ) ( ) ( ) { } [ ]
=
+ =
N
i
i i
x Z h x Z
N
h
1
2
2
1

where:
) (
i
x Z are the data.
x
i
are the locations such that data are available at both x
i
and ) ( h x
i
+
) (h N is the number of pairs of points actually taken into the sum when
calculating ( ) h . If data are missing, the pair is simply ignored.
Suppor t
Variograms must be
calculated on data of even
support.
110

If several lines of samples are available, for example several profiles in soils
sampling, parallel Ditch Witch lines, numerous drill holes, etc., then we can
compute the average variogram for a group of parallel lines.
If the spacing along a line is not constant we can either:
Regularise the data by compositing to an even interval: this is the usual
approach when calculating a 1-D variogram in mining.
Group samples by classes of distance, i.e. a distance tolerance is applied.
2-D: In a Pl ane
Calculation of the experimental variograms in two dimensions is required in many
mining situations:
In the plane of a mining bench, for example in grade control.
For a bed or other stratiform feature, for example seam thickness in coal
mining.
In the plane of a vein.
For modelling topographic data or geological surfaces.
When considering data collected at points on a surface, for example,
exploration soil geochemistry.
When calculating the variogram in a plane, at least four directions should be used
to check for anisotropies. In the case of a regular grid, calculation of the
experimental variogram is essentially similar to that of parallel profiles considered
above. The variogram should be computed in four main directions. Note that the
lags are different in length along the diagonals of the grid, see figure 6.1.
If the data are not on a regular grid, then we calculate the variogram for various
angular classes and also specify a distance (or lag) tolerancesee figure 6.2. We
search a sector of a circle between two arcs. We will make some general comments
on lag and angular tolerances later.

Figure 6.1 Lag distances are unequal, even for an isotropic) grid mesh

111

3-D
In three dimensions, we generalise the two-dimensional approach so that our
search is in a conical segment of a sphere, rather than a sector of a circle. Otherwise
the principle is the same. Of course, in addition to a bearing or azimuth, we must
also define a plunge to uniquely specify each direction.
In practice, the third dimension often plays a unique role. There is often much
more variability in the third dimension.
Thus, when calculating variography in three dimensions, we commonly have one
direction that is much more closely sampled than the others, for example: across
the vein might also be down the hole. In this case, we logically define this as a
direction to calculate variograms, and the down-hole (1-D) variogram will
approximate the across the vein direction. The same case applies in deposits
drilled by vertical (or steeply angled) holes: the down hole variogram here
approximates the vertical direction.

Figure 6.2 Searching in 2D
Down t he hol e
In 3D the down hole
direction usually has the
closest spaced samples, and
is thus preferred when
estimating nugget effect.
112

Addit ivit y
In almost all applications of geostatistics, the variables we study must be additive
16
.
Variables are additive when the mean over a certain zone is the arithmetic mean of
the values. This is not always the case, so lets look at an example.
An Exampl e
Suppose that we wish to find the average vein thickness and gold grade in the
simple case illustrated in figure 6.3. There are two core intersections: one with a
grade of 5 g/t and a thickness of 2m, the other with a grade of 10 g/t and a
thickness of 3m.

Figure 6.3 Example of additivity (see text for calculations and discussions)

16
An exception to this is where we wish to use kriging purely as an interpolator to generate a grid to be
used for subsequent contouring .
Addi t i vi t y
Not all variables can be
averaged!
2 m
5 g/t
3 m
10 g/t
Core 1 Core 2

113

Clearly, the average thickness is simply the arithmetic mean, i.e. 2.5 m. However,
simply calculating the arithmetic mean of the two grades would give us a false
result:
average gold grade = 7.5 g/ t Au
5 10
2
+
=
Using a simple arithmetic mean of grades would give a biased estimate of the mean
grade of the area sampled by the two cores. The average gold grade is obviously not
the average of the two gold grades, but the weighted average, weighting by the
intersection thickness:
average gold grade = 8 g/ t Au
2 5 3 10
2 3
0
+
+
= .
114

The product of grade and thickness is a variable usually called accumulation. In an
estimation where we wish to use accumulations (and this is a traditional approach
in mining geology) we perform the entire geostatistical study on two variables:
accumulation and thickness. At the end of the study, we divide the kriged
accumulations by the kriged thicknesses to obtain an estimate of grade.
The accumulation is proportional to the metal content if the specific gravity is
uniform. Note that, if we have variable specific gravity and can assign an SG to
each intersection, then it is more strictly correct to use the triple accumulation, i.e. the
grade multiplied by the thickness multiplied by the SG.
The accumulations (or triple accumulations) are additive, and thus we can
legitimately use them for geostatistics. The other approach would be to model the
vein in three dimensions using samples of equal length, which in many geologically
simple situations is more complex and more prone to error.
Another example of non-additive variables is permeability. Although we can treat
porosity as being additive, permeability is scale dependent and cannot generally be
treated as additive.
Models for Variograms
When we calculate the experimental variogram, we obtain a discontinuous function:
for each of a finite set of lag distances h we have an experimental value of ( ) h .
We cannot use the discontinuous experimental variogram as a weighting function
for estimation, we require a continuous function. In order to use the variogram for
estimation (kriging), or any other inferential purpose, we therefore need to fit a
mathematical functionor variogram modelto our experimental variography.
Most variograms have quite simple forms, much of the apparent fluctuation being
due to sampling or statistical effects. The functions used to fit models are thus
usually fairly simple. However, not just any function is acceptable as a variogram
model.
Not Any Model Wil l Do!
The variogram model is a mathematical model for spatial variability: not any model
will suffice. The reason is simple: when the dispersion variance or estimation
variance are calculated from the variogram model a positive variance must result. This is
not optional! In a mathematical and intuitive sense, a negative variance is
unacceptable and meaningless.
Admi ssi bl e Li near Combi nat i ons
As we discussed in the first part of this course, most estimators used in ore reserves
applications are linear combinations of the available data.
We will be developing an optimal estimator that is a linear combination in Chapter
9 (kriging). We will need to be able to calculate the variance of linear combinations,
for example:
Ac c umul at i on
While the grade on variable
length samples may not be
additive, the length-weighted
grade (accumulation) is
additive.
115

( )
i
N
i
i
x Z Z =
=1
*

In the case of a stationary variable Z(x) with a covariance function C(h). The
variance of the linear combination can be shown to be:
( )
) (
Var Var
1
*
j i j
i j
i
i
N
i
i
x x C
x Z Z
=
=

Where C x x
i j
( ) is the covariance between the two locations x
i
and x
j
.
The variance of the quantity Z* (i.e. the linear combination) must be non-negative
for any points x
i
and x
j
we consider; and non-negative regardless of the weights
i

we select.
A function that satisfies this condition is said to be positive definite or, more strictly
speaking conditionally positive definite.
We won't go into the argument here for why we must choose a function that
satisfies this condition (an interested reader is referred to Armstrong and Jabin,
1981, with a good example). But it must be understood that variogram models
must be positive define functions.
Be warned also that some models may be admissible, say, in one or two
dimensions, but not acceptable for modelling a three dimensional variogram!

From a Pract i cal Viewpoi nt
From a practical point of view this has a very straightforward implications:
There exists a set of admissible models for variograms. These models are
conditionally positive definite.
Not using one of the accepted models can result in negative variances, and
this is clearly unacceptable.
The user of geostatistics should therefore only use known, authorised
variogram models.
This may sound restrictive, but in practice it isn't, because just a few of the available
admissible models (or combinations of them) will model any experimental
variogram the mining practitioner is likely to encounter.
Some Common Models
116

We outline here the more common models that are provided for in geostatistical
software. All these models are admissible, i.e. conditionally positive definite.
The Spheri cal Model
Figure 6.4 shows the spherical model
17
.

Figure 6.4 Spherical Model
This is the most commonly used variogram model; it is often fitted with the
addition of a nugget effect model (see next section). The spherical model (or
spherical scheme) is available in any commercial mining geostatistical software.
Most generalist mine modelling packages that incorporate a kriging module include
the spherical model.
The reason for the popularity of the spherical model is simple: with a combination
of spherical models and a nugget effect, nearly all experimental variograms
commonly seen in mining applications can be fitted.
The spherical model has a simple polynomial expression and is defined as follows:
a for ) (
a for
2
1
2
3
) (
3
3
> =
=
h C h
h
a
h
a
h
C h

where a is the range of the variogram and C is the sill (as defined in the previous
chapter).The spherical model matches well what we often see for mining variables:

17
The name spherical comes from the fact that the associated covariance of the spherical variogram
model, i.e.
C h C h ( ) ( ) =
This is proportional to the volume of the intersection of a sphere of diameter a with a similar sphere
translated by h.
Spher i c al Model
In mining applications, the
spherical model is sufficient
for most situations.
117

a quasi-linear behaviour near the origin followed by stabilisation at the sill. The
spherical model, having a sill, is a transitional model, i.e., we can model a transitional
behaviour going from correlation, at distances less than or equal to the range a, and
lack of correlation at distances beyond this.
Note that the tangent at the origin intersects the sill at 2/3 of the range. Although
originally derived in 3D, the model is admissible in 2D or 1D.

Power Model
Power function models (figure 6.5) are commonly implemented in geostatistical
software. These models have no sill, i.e. are not transitive, and are of the form:

( ) h h =
with being a power between 1 and 2. A particular case is the linear model, where
is equal to 1.0 (this model is sometimes useful in mining applications). The linear
model is thus:
( ) h h =
and is the slope of the variogram. For the linear model, the value of the
variogram is simply proportional to h. Many grade variograms have more-or-less
linear behaviour near the origin, for example spherical types of variogram.
As we shall see later, the near origin behaviour of the variogram is a major factor
influencing the results of kriging. Consequently, the linear model has been much
used, in part because of its simplicity (especially in the early hand-cranked days of
geostatistics).

Power Models
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
h (lag)
g
a
m
m
a

(
h
)
p=0.01
p=0.2
p=0.5
p=1
p=1.3
p=1.6
p=1.9

Figure 6.5 Power Function Models
118

Figure 6.6 Exponential Model
For power models with less than 1.0, the power model has a convex shape, not
unlike the spherical model, but steeper (indicating less continuous behaviour than
the spherical model).
For greater than 1.0 the power models have a concave shape at the origin,
indicating very continuous behaviour at short distances. This kind of behaviour is
not frequently seen in mining applications. In fact, for =2.0 we have a parabola,
and smooth differentiable behaviour (unheard of in mining applications).
Consequently, caution should be used with setting of the parameter if one
decides to employ this model.
Exponent i al Model
The exponential model (see figure 6.6) is of the form:
=

a
h
e C h 1 ) (
Where C is the asymptote shown in figure 6.6. Note that a here is not the range (as
defined for the spherical model, for example) but is a distance parameter
controlling the spatial extent of the function.
The exponential model looks quite similar at first glance to the spherical model and
it is used to model transitional phenomena. Since the exponential variogram
asymptotically approaches the sill, the practical or effective range is
conventionally defined to be 3a (the variogram is at 95% of the sill at this distance).
Although sometimes applicable for mining data, this model finds more use in non-
mining applications, for example soil chemistry (Webster and Oliver, 1990).
Gaussi an Model
War ni ng!
Take care: powers > 1.0
infer highly continuous
behaviour not normally seen
for grade variables.
119

The Gaussian model (figure 6.7) is sometimes implemented in geostatistical
software. The form is:
=

2
2
1 ) (
a
h
e C h
Where, as for the exponential model, C is the asymptote (shown in figure 6.7).
Note that, again, a is not the range but a distance parameter controlling the spatial
extent of the function. The practical range for the Gaussian model is 1.73a (again,
this is the distance at which the model reaches 95% of the value of the sill.
The Gaussian model represents extremely continuous behaviour at the origin. In
practice, such a variogram is implausible for any grade variable. Its only possible
application is for very smooth, continuous variables like topography. Some
geological surfaces might be reasonably modelled by a Gaussian variogram. If
available, the cubic model (see below) might be more suited, in general.
However, it is critical to know that this model, if used for kriging, should always be
combined with a small nugget effect (say a few percent of the sill) to avoid
numerical instabilities in the kriging.
Cubi c Model
The cubic model

(figure 6.8) is defined:
a C h
a
a
h
a
h
a
h
a
h
C h
> =
+ =
h ) (
h
4
3
2
7
4
35
7 ) (
7
7
5
5
3
3
2
2

The cubic model is smooth at the origin, in the manner of the Gaussian model, but
not so smooth. Its overall shape is reminiscent of the spherical model, and if an
experimental variogram presents very continuous behaviour, it is generally
preferred to the Gaussian model. It is available only is specialised geostatistical
packages such as Isatis.
War ni ng!
The Gaussian model
represents extremely continuous
behaviour at the origin. In
practice, such a variogram is
implausible for any grade
variable.
120

Figure 6.7 Gaussian Model

Figure 6.8 Cubic Model (Spherical for Comparison)

Models for Nugget Effect
In the previous chapter we defined the nugget effect as the discontinuity of the
variogram at the origin. We gave the nugget effect a simple, physical interpretation:
if measurements are taken at two very close points x and x+h, the difference:
{ } [ ] Co x Z h x Z E +
2
) ( ) (
121

where Co is some value greater than zero. The value Co is the nugget effect. While
the variogram is defined as being equal to zero at zero distance, in practice
discontinuities are usually observed for mining data.
Note that the nugget effect implies that values have very short scale fluctuation.
To model the nugget effect we require a function for the variogram that assumes
the value zero at the origin and a constant value for all values greater than this. The
equivalent model for covariance has a value 1 at the origin and 0 elsewhere. To
achieve this we use a mathematical function that has these properties, called the
Dirac function ( ) h . The resulting model for nugget effect is:

( ) { ( )}
( )
h Co h h
h h
=
=
1 0
0 0
for
for =

Note that, strictly speaking such a model is only possible for variables that have
discrete values. For mineralisation occurring as nuggets or grains that are small in
comparison to the sample support this is not too problematic. However, some
geological variables (for example depth to a geological surface) are clearly
continuous. Even with such variables, we do often need the addition of a nugget
effect model to obtain a satisfactory fit for the variogram. We discuss several
reasons why the addition of a nugget effect is necessary for these variables below
(widely spaced data, sampling errors, locational errors).
It's apparent that things are somewhat complicated when it comes to modelling the
nugget effect, so we will discuss a few of the issues involved in some detail.
Apparent vs. Real Nugget Effect
The nugget effect has the units of variance, and is sometimes called the nugget
variance. The nugget effect is, in fact, that proportion of the variance that cannot be
explained by the regionalised component of the regionalised variable (see previous
chapter). Note that the case of complete absence of spatial correlation is referred to
a pure nugget effect. In reality, mineralisation rarely exhibits this type of behaviour,
because, although grade variablesespecially precious metal gradesare usually
expected to have some natural chaotic behaviour at very short scales, there are
other contributions to the nugget effect.

Int egrat i on of Mi crost ruct ures
One of the main difficulties here is that there is a minimum distance below which
the variogram is unknown, i.e. at distances smaller than the first point of the
variogram (at lag 1).
The usual procedure is to extrapolate from the first point to locate the intercept
with the ordinate (Y) axis. If the extrapolation results in a positive Y intercept, this
is taken as evidence of the presence of a nugget effect of magnitude Co.
122

On the other hand, if the curve goes through the origin, we surmise that there is no
nugget effect (or a negligible nugget effect).
There is a risk of being wrong in both cases (see figure 6.9).
1. We may obtain closer spaced sampling information that reveals our
variogram does in fact tend to zero at short lags. In this case an
unsuspected short range structure may exist. Our apparent nugget
effect is actually due to the data being too sparsely or widely spaced.
2. Alternatively, the observed variogram points lead us to extrapolate the
variogram to the origin where as, in fact, the variogram flattens at lags
shorter than the available data. This type of behaviour is typical of the
contribution of locational errors to the nugget effect.

Figure 6.9 Apparent nugget effect and missed nugget effect.
While the geostatistician may be able to hypothesise about the short-scale
behaviour of the variogram by using some a priori knowledge, in general it is better
to have close spaced information available.
The shortest, inter-sample distances limit our resolution of the variogram. Without
such information, short-scale structures cannot be resolved. In such a case, any short-
range nested structures will be unresolved and appear as nugget effect.
Geostatisticians refer to this incorporation of short structures into the apparent
nugget as integration of microstructures. In a sense, this is always unavoidable,
because even with exhaustive sampling of the mineralisation, we cannot resolve
short-range structure at the scale of our samples (say, cores) or less.
In summary, when modelling the nugget effect one should be aware that closer
spaced sampling can often reduce the nugget effect.
Isot ropy and t he Nugget Ef fect
The most closely sampled direction in mining situations is usually the down the
hole direction. Since the nugget effect is strictly defined for very small distances
h 0, it is independent of direction. This has important practical implications:
1. In general, the most closely sampled direction should be used to
reliably determine the nugget effect.
Cl ose-spac ed
Sampl i ng
The down hole variogram is
invaluable in estimation of
the nugget effect.
I sot r opy of Co
The nugget effect is
isotropic: i.e. it has a single
value for a variogram model,
even if the spatial
components of that model
are anisotropic.
123

2. It is incorrect to model the nugget effect with different values in
different directions. The nugget is not allowed to be anisotropic!
Sampl i ng Error and t he Nugget Effect
Often we can know the variance of the errors associated with sampling. This is a
large subject in itself, and the reader is referred to publications by Francois-
Bongarcon (1991, 1992, 1993, 1996), Francois-Bongarcon and Gy (2001), Pitard
(1990a, 1990b) and, in particularfor a discussion of the linkage between Gy's
sampling theory and the nugget effectto the paper of Ingamells (1981). The
importance of minimising sampling errors is quite obvious in any case, but it is
clear that our variography will be affected by the contribution of sampling errors to
the human nugget effect.
Locat i onal Error
Locational error occurs when a sample that is associated in our database with the
point x (where this location may be in one, two or three dimensions) was actually
measured at some different location x+u. Again, this is a measurement
contribution to the nugget variance. In this case, instead of studying a variable Z(x),
we actually study:
Z x Z x u
1
( ) ( ) = +
If this measurement error is constant, for example, our grid is wrongly located 10m
to the east, there is no impact on the nugget effect. However, if this error is not
constant (even if it is systematic, but variable) we will add to the nugget effect.
Combi ning Model s
All the models we have introduced here describe simple curves or straight lines.
The real live experimental variograms that are encountered in mining (and other)
applications will often appear more complicated and none of the models listed
above will seem to be appropriatea more elaborate shape may be necessary to fit
the experimental curve.
Fitting models to such variograms is best done using combinations of two (or
more) of the above models. This is allowable, because any linear combination of
authorised models is, itself, authorised. The models are simply added together:
( ) ( ) ( ) ( ) ... h h h h = + + +
1 2 3

A common addition is to add together a spherical model and a nugget effect
model, this is usually summarised as:
a for ) (
a for
2
1
2
3
) (
3
3
> + =
+ =
h C Co h
h
a
h
a
h
C Co h

Co indicating the nugget effect model.
Er r or and Nugget
The nugget effect in essence
captures the noise in the
data. This may come from
database errors as well as
from the inherent nuggetty
nature of the grade.
124

For geological data, especially grade or geochemical data, it is common to see two
or more recognisable spatial components in the variogram, generally called nested
structures (see previous chapter). Figure 6.10 shows an example of this type of
variogram. Note that we refer to the spherical models as Sph1 and Sph2. In
general, a nugget effect plus 2 or perhaps 3 spherical structures will suffice. The
addition of more than 3 models (plus nugget) doesn't usually result in much
difference to the shape.
The nested model in figure 6.10 would be written as follows:
2 2 1
2 1 3
3
2 1
1 3
3
2 3
3
1
for ) (
< for
2
1
2
3
) (
for
2
1
2
3
2
1
2
3
) (
a h C C Co h
a h a
a
h
a
h
C C Co h
a h
a
h
a
h
C
a
h
a
h
C Co h
> + + =
+ + =
+ =

Figure 6.10 Example of combining models nested spherical models with nugget effect.
Anisot ropic Models
All the models discussed so far describe isotropic situations. In such a case, the
variogram is only dependent upon the modulus or absolute value of h, i.e. only
upon h , and not upon direction.
Geol ogi c Pr oc ess
The nature of most mineral
deposits is that some
anisotropic structural or
sedimentary (or other)
control is evident. Thus we
expect anisotropy of
variogram in most cases.
125

As we discussed in the previous chapter, there are many geological situations where
we expect anisotropy, i.e. where we expect the variation to be different depending
upon the direction in which we calculate the variogram.
We introduced, previously, the two types of anisotropy:
1. Geometric anisotropy
2. Zonal anisotropy
Geomet ric Anisot ropy
Geometric anisotropy (also called elliptical anisotropy) can be corrected by a simple
linear or affine transformation of the coordinates. In the case of geometric
anisotropy, for a transitional variogram, the sill of variograms in each direction is
the same. Only the range is different. In the case of a linear variogram it is the slope
that is directionally dependent.
We can plot the range (or slope, in the case of a linear variogram) as a function of
the direction. For geometric anisotropy, the plot approximates an ellipse (in 2D, an
ellipsoid in 3D); a simple change of coordinates transforms this ellipse into a circle,
eliminating the anisotropy.
It's important to understand that, when calculating the experimental variogram we
choose at least four directions. This is because choosing only two directions may
not detect a geometric anisotropy, even if one is present.
Fitting the model for geometric anisotropy in simple cases presents few difficulties.
Firstly, we calculate the experimental variogram in at least four directions in the
plane, plus in the vertical or down-hole direction(s). We determine which directions
have the longest and shortest ranges (these may not correspond to the axes of the
information grid, so care must be taken).
For the two dimensional case there will be two principal directions at right angles
to each other. In three dimensions there will be three mutually perpendicular
principal directions. Fit an anisotropic model to the experimental variograms in
these principal directions as follows:
1. Fit the model to the experimental variogram for the best-defined
principal direction.
2. Choose the next clearest experimental variogram in one of the
remaining principal directions. Divide the range of each spatial
structure in your variogram model (i.e. the model for the direction
fitted in the first step, above) by a factor. Choose these factors such
that the model is compressed (dividing by factors greater than 1.0) or
stretched (divided by factors less than 1.0) in order to obtain a model
that fits in the second principal direction.
3. Repeat the second step for the remaining principal direction, if you are
working in three dimensions.
126

In general the convention is to specify anisotropy factors or anisotropy ratios as numbers
that we divide the ranges by. If the range of a structure is 100m in the first direction
we fit, and needs to be 50m in the second, then the anisotropy ratio is 2.0.
Conversely, if the range of the structure is 40m in the first direction we fit, and
needs to be 80m in the second, then the anisotropy ratio is 0.5.
For nested models, the anisotropy can be complicated. For example, the ratios
might be different for each component structure.
Note, however, that some software may use a multiplying convention.
An Exampl e
The anisotropy ratios are usually specified for each direction, so that the reader of a
report knows which direction is the reference direction. For example, figure 6.18 in
the structural analysis case study (at the end of this chapter) we will specify the
variogram model (in 3D) as shown in table 6.1:
Table 6.1 Model for Variogram
(ranges expressed using anisotropy ratios)
Nugget Sph1 Sph2
Sill 0.026 0.017 0.034
Range 0 20 150.
X-anis 1.00 1.50 5.00
Y-anis 1.00 1.00 1.00
Z-anis 1.00 1.50 4.00

127

In this case the range of the longest structure (north-south, or Y-direction) was
fitted first. In addition to a nugget effect model (range 0), two nested spherical
models, denoted Sph1 and Sph2, were fitted with ranges of 20m and 150m
respectively. The anisotropy ratios then give us the ranges in the other directions,
by division:

Note that the nugget effect model has no range and is isotropic, by definition.
The anisotropy is different for the short vs. long structures: for the short structure
the resulting model is close to isotropic, whereas for the long structure, there is
strong anisotropy. We discuss this model in more detail in the case study, later in
this chapter.
For unbounded variogram models (e.g. power models, including linear models) the
affine transformation to model geometric anisotropy is applied by changing the
gradient of the model. In the case of a linear model, this is simply the slope.
Zonal Ani sot ropy
More complicated types of anisotropy exist in some deposits, for example where
distinct zonation of high and low values exist. In this case the variability in the
direction parallel to the direction of zonation might be significantly lower than in
the direction perpendicular to zonation. This concept is usually called zonal
anisotropy.
Zonal anisotropy cannot be modelled in most general mining packages. Even
where it can be modelled, the model often can't be used for kriging. Modelling of
zonal anisotropy is beyond the scope of this course. The interested reader is
referred to Journel and Huijbregts (1978, pp. 266-272) for a case study.

Table 6.2 Model for Variogram
(ranges in metres in brackets)

Nugget Sph1 Sph2
Sill
0.026 0.017 0.034
Range
0 20 150.
X-anis
1.00 (0m) 1.50 (13.3m) 5.00 (30m)
Y-anis
1.00 (0m) 1.00 (20m) 1.00 (150m)
Z-anis
1.00 (0m) 1.50 (13.3m) 4.00 (37.5m)
Pr ac t i c al i t i es
Zonal anisotropy cannot be
modelled in most general
mining packages. Even
where it can be modelled,
the model often can't be
used for kriging.
128

Why Not Aut omat ed Fit t ing?
A common question is: why not fit the variogram automatically? Geostatisticians
have had access to automated variogram modelling software for years (weighted
least squares, etc.). However, most experienced geostatisticians will fit models
manually.
There are two main reasons for this. Firstly, the modelling must take into account
the fact that the most important parts of the variogram to fit accurately are the near
origin lags. Often, the first point is under-sampled, so some trade off between the
number of pairs contributing to the lag (reliability) and the need for the model to
respect the near origin points is required. In many cases this is relatively easy to do
subjectively, but difficult to do algorithmically.
Secondly, our problem is compounded when we are faced with noisy (or poorly
defined) experimental variograms, where considerable external input to the
modelling process is necessary. For example, we might employ a priori geological
knowledge to adjust the range of a structure. Software can't be expected to mimic
this. An intelligent operator with site-specific geological knowledge is required.
This point emphasises that geostatistics is not suited to black box usage: if you have
access to software that makes an automatic fit, treat this as a first guess and then
adjust the model intelligently to obtain a satisfactory final fit.
Syst emat ic Variogram Int erpret at ion
Some geostatistical textbooks may leave the reader with the impression that fitting
variograms is a fairly easy task. In many cases, especially when dealing with
precious metals data, this is far from true. Having a systematic approach is
important when first setting out to perform variographic analysis. We'll tackle
seriously troublesome variography later, but for the moment we consider here the
usual procedure for modelling variograms.
In fact, fitting variogram models is as much a craft as a science, in the sense that it
isn't an activity that can be completely reduced to a formula. Repeated experience
fitting variograms increases the practitioners skill. However, we present some
guidelines intended to help you with variogram modelling.
Obviously, not all the following comments will apply to every experimental
variogram you'll encounter. However, it's especially useful when first dealing with
structural analysis to have a few pointers.
Ten Key St eps When Looki ng at a Vari ogram
We consider key points to look for when examining experimental variography.
Always remember that the experimental variogram is an estimate of the
underlying variogram. As such some irregularity is generally expected, due to
statistical fluctuation.
Bl ac k box es
Software can't be expected
to mimic skilled variogram
modelling. An intelligent
operator with site-specific
geological knowledge is
required
Sk i l l &
Ex per i enc e
Fitting variogram models is
as much a craft as a science,
in the sense that it isn't an
activity that can be
completely reduced to a
formula
129

1. The number of pai rs for each l ag i n t he experi ment al vari ogram.
The number of pairs contributing to the first lag (the first point of the experimental
variogram) can often be quite low. This will depend upon the exact sampling
pattern and search used. Consequently, the first point may not be very
representative. Some software annotates the experimental variogram with the
number of pairs used. So long as a listing is available, we can check to see that
points at short lags are reliable.
Although rules are difficult to apply strictly, fewer than 30 pairs is likely to be
unreliable in any mining situation. Note that the number of pairs should be
considered in proportion to the size of the data set, for an experimental variogram
with 2,000 pairs at lag No. 2, lag 1 might be considered dubious with 100 pairs. See
figure 6.11a.
Similarly, at distal lags, the number of pairs decreases. It's easy to see why: with
increasing distance there comes a point where only samples at the very edges of our
area can be used. It can be shown theoretically that the variogram can become
dangerously unreliable at lags beyond 1/3 of the maximum sample separation. See
Figure 6.11b.
2. Smoot hness of t he experi ment al vari ogram
The smoothness of the experimental variogram in figure 6.11a and 6.11b can be
contrasted to the more erratic behaviour in figures 6.11c and 6.11d. Many factors
can contribute to erratic variograms, and we'll discuss these in detail, in the section
on troublesome variograms below.
However, two types of erratic variography can be distinguished. In figure 6.11c, the
experimental variogram is saw-toothed in a regular up-and-down fashion. This may
indicate poor selection of lags or possible inclusion/exclusion of a very high value.
In any case, the structure is still visible. If we exclude other sources of irregularity,
this variogram might be modelled in an averaged way, as shown in the figure.
Some of the techniques discussed below in the section on troublesome variograms
might result in a cleaner variogram.
On the other hand, figure 6.11d shows a noisy variogram with no obvious
structuring, nor is there clearly evident the kind of saw-toothing behaviour seen in
figure 6.11c. In this case we have to resort to some kind of robust variography
(relative variograms) or transformation (logs, etc., see further, below).

130

Figure 6.11 Common real life experimental variogram features

131

3. Shape near t he ori gi n
It's critical to assess the shape near the origin correctly. As we've already said, the
first points are sometimes suspicious or unrepresentative. In mining applications,
especially for grade variables, the shape at the origin is nearly always linear. This is
one reason that the spherical model is so popular.
If the experimental variogram suggests a parabolic shape near the origin (like the
Gaussian model introduced above) be very cautious. This will nearly always be a
statistical feature when dealing with grades. Resist the temptation to fit Gaussian
models! The consequences for kriging are quite profound: the Gaussian model
represents extraordinarily continuous, smooth short-scale behaviour of a type not
seen for mineral grades. In the case of topographic variables (depth to a geological
surface, the water table, vein width, etc.) caution is still advisable.
If you are convinced that a topographic variable is Gaussian, then always fit the
model with a nugget effect (in order to avoid instability in subsequent kriging). In
many cases, a cubic model is preferred, but this model is not generally available in
mining software.
The slope of the variogram near the origin is a critical factor in subsequent kriging.
Greater weight is generally given to the experimental points closest to the origin
when assessing this slope (given that these points have a reasonable number of
pairs contributing). Note that the slope is relative to the ratio of the range to the
proportion of nugget effect.
4. Di scont i nui t y at t he ori gi nnugget effect
Along with the shape and slope at the origin, the proportion of nugget effect is a
critical factor in modelling the variogram. Most grade variables have some nugget
effect. The proportion of nugget effect relative to the sill is often called the relative
nugget effect , and is measured as a ratio to the sill:
=
+
Co
Co C

The relative nugget effect is often expressed as a percentage.
The nugget effect is the same in any direction (being defined at very small distances
relative to the sample spacing). Because of this, in mining we will generally use the
down hole direction to set the nugget effect and then use this value for each of the
other directions.
Note also that the relative nugget effect is dependent upon compositing length (i.e.,
for a given spatial grade distribution, as we use longer composites, is reduced).
We discuss this phenomena (related to support effect) in more detail in the next
chapter.
5. Is t here a si l l ?t ransi t i onal phenomena
I mpor t ant Not e:
If the experimental
variogram suggests a
parabolic shape near the
origin (like the Gaussian
model introduced above) be
very cautious

Co i s I sot r opi c
Because of this, in mining
we will generally use the
down hole direction to set
the nugget effect and then
use this value for each of the
other directions.

132

Answering this question is sometimes not as easy as you might expect. For
example, take figure 6.11e. Here we have an example of an experimental variogram
(I) that clearly has a sill. However, variogram II seems to continue to rise. We may
have a linear (or unbounded) variogram, but equally, we may not have yet reached
the range of a transitional model. For example, we have been restricting the zone
upon which we calculate the variogram too severely. Then again, it is possible we
have a drift (see further below).
Note that, so long as the shape of the function we choose fits the experimental
data well, especially near the origin, the difference between choosing linear or
spherical (with a very long range) is negligible.
If the sill level is not clearly defined (for example figure 6.11c) then we often use
the average level of fluctuation. If this corresponds to the variance of the data (as
it should in the stationary case), our confidence is increased.
Although the sill should coincide with the overall variance (in conditions of
stationarity), this is not always the case, for example because of the presence of
long-range trends in the data. Note that the level of the sill for the longest
structures in a nested model has little impact upon kriging weights, so in most cases
fixing it with great precision is not necessary.
6. Assess t he range
If we do have a transitional model, then we need to assess the range. In general, the
range is assessed visually, as the distance at which the experimental variogram
stabilises at a sill.
In many cases, the range is fairly clear, especially for experimental variograms that
closely approximate a spherical scheme. In other cases, it may not be so easy.
Firstly, bear in mind that there are some mechanisms for specifying range inherent
in the functional forms of the model we choose. In particular, the linear
extrapolation of the slope at the origin should cross the sill at 2/3 of the range for a
spherical variogram. If the sill is clear, this rule of thumb can be quite helpful. In
this case, the first few reliable points of the experimental variogram, not those close
to the range, should control the slope.
Careful definition of the ranges of shorter structures (when more than one
regionalised structure is evident) is very important.
7. Can we see a dri ft ?
Drift is not so easy to detect in many mining situations. Firstly, at lags beyond
about 1/3 of the maximum available sample separation, theory indicates that the
variogram becomes increasingly unreliable. So a continuously rising experimental
variogram, such as that shown in figure 6.11f may be quite misleading. Again, look
at the representivity of the pairs.
Assessing a drift should also be made in conjunction with examination of a posting
of the data, or a contour map. Look for trends that might clearly be responsible.

Sl ope
The first few reliable points
of the experimental
variogram, not those close
to the range, should control
the slope.

133

Some software will print out, for each lag, the number of pairs, the mean of the
pairs and the drift, this being the mean value of the pairs for this lag. Of course,
systematic increase in this statistic for distal lags is still only significant if we have
sufficient pairs.
Even where a convincing case can be made for a drift for larger lags, this may have
little impact on subsequent kriging. This is because, as we have repeated regularly
so far, the shape of the variogram at shorter lags is the critical factor in the results
of any subsequent kriging.
In most mining situations, modelling of drift is not required. If it is required, there
are techniques available, but these are beyond the scope of this course (see Journel
and Huijbregts, 1978, p.313).
8. Hol e eff ect
A hole effect appears as a bump on the variogram. As stated in the previous
chapter, most apparent "hole effects" are, in fact, an artefact of the sampling used,
lack of pairs etc. Although hole effect models exist, they are beyond the scope of
this course and their use is not common.

9. Nest ed model s
Given an interpretable experimental variogram we will usually need to model more
than one structure. In the simple case, we assess the nugget effect and then fit a
single, say spherical, model for the structured component.
In many cases, mining data present more than one range. Clear inflections in the
experimental data indicate the ranges of nested spherical models. We see several
examples of this in the case study at the end of this chapter.
Generally, where several models are nested, fitting the model with the shortest
range will prove critical (from the point of view of subsequent kriging).
10. Ani sot ropy
It is essential that the experimental variogram be calculated in at least four
directions in the plane, and at geologically sensible orientations in the third
dimension, in order to detect anisotropies. The procedure for fitting an anisotropic
model was discussed in the preceding part of this chapter.
In the absence of any detected anisotropy, an isotropic model can be fitted.
Fitting of zonal anisotropy is beyond the scope of this course.

I mpac t of Dr i f t
Even where there is a drift, ,
the shape of the variogram
at shorter lags is usually the
critical factor in the results
of any subsequent kriging.

134

Uncooperat ive or Troublesome Variograms
18

If the experimental variograms encountered in practical situations were as well
behaved as those often given as textbook examples, this section would be
unnecessary! In fact, the reader is unlikely to avoid horror variograms like the one
shown in figure 6.11d for very long (if they are working in a gold mine, sooner
rather than later).
We will approach the subject of uncooperative or troublesome variograms via two
different angles:
1. Can we improve variography by choosing different calculation
parameters?
2. Can we deal with the problem by some approach more sophisticated
than calculation of the traditional grade variogram?
Cal cul at i on of t he Experi ment al Vari ogram
We examine here a number of factors we should check first when confronted by a
dreadful-looking experimental variogram. The initial experimental variograms are
often highly erratic and time, effort and thought is required to establish why this is
so. The paper of Armstrong (1984) gives some excellent examples (some of which
are discussed here).
Theoret i cal Reasons
The experimental variogram is an estimate of the spatial structure. As such, it is often
highly variable for large values of h. Various geostatisticians have demonstrated
that, when we have a very large number of closely spaced data (for example from
blast hole drilling or a simulation), subsets of this data can have widely varying
histograms and variography.
Defi ni t i on of St at i onary
Sometimes the reason for poor variography is that we are calculating the variogram
from two mixed populations that possess differing statistical characteristics. In an
extreme case this will show up as a bimodal histogram, but this is certainly not
always the case (Armstrong, 1984). Since the variogram assumes intrinsic
stationarity, mixed populations can impact severely on the experimental variogram.
Where possible, our variogram should therefore be calculated for a single statistical
population.
GEOGR AP HI CAL L Y DI S TI NCT P OP UL ATI ONS
If the populations are geographically distinct, i.e. they can be outlined on maps of
the deposit, then our problem is to define the boundaries of our zones. This is
partly iterative, in that the variogram is one aspect of the evidence we will use to
split or lump geological zones. Combining zones with quite different geostatistical

18
i.e. the usual variety for mining examples
St at i onar i t y
The stationarity decision is
probably the most important
decision in a geostatistical
study.
135

characteristics can result in poorly defined and sometimes uninterpretable
variography.
Alternatively, if we split the zones into too many categories, we may end up with
too few data in each zone, thus statistical fluctuations may overwhelm the
underlying spatial structure. Obviously, some experience and trial-and-error is
involved.
I NTE RMI XED P OP UL ATI ONS
The problem may be more intractable. For example, if the two populations are
related to intimately intermingled, but statistically contrasting lithologies, then the
only means to resolve the problem may be more detailed sampling (i.e. closing up
the drilling further).
Another example of intermixed populations might be mixing two or more
different drilling campaigns. It is often the case that older campaigns have smaller
diameter drilling, poorer sample preparation etc. The result of this is artificially
higher variance for the older drilling campaign. This may be revealed by higher sills,
shorter ranges and in extreme cases, apparent pure nugget behaviour of the
variogram.
How t o Det ermi ne Appropri at e Vari ogram Cal cul at i on
Paramet ers
The parameters relating to search tolerances and lag selection are sometimes very
sensitive.
Lag Sel ect i on.
A strongly pronounced saw-toothing of the experimental variogram, as shown in
figure 6.11c, is a warning that we may have poorly specified the lag increment. If
the data spacing is irregular, the basic lag interval to choose may not be immediately
obvious, and we may get a situation where successive lags include larger, then
smaller numbers of pairs in a cyclic fashion. The lags with fewer pairs will be less
robust to extreme values, and tend to haveon averagehigher values of ( ) h .
Tol erances
In particular, selection of the lag and angular tolerances can sometimes have a
drastic impact on the variogram. If the variogram looks bad, try larger or smaller
tolerances. In doing so we are, in a sense, varying the smoothing the data in order
to lessen the impact of including or excluding particular pairs in a given lag. The
angular tolerance can be especially sensitive to this type of effect.
Mi ssi ng Val ues
Most programs allow specification of a minimum value to consider in calculation
of the variogram. It is common to flag missing values with a negative number, say -
1. If we do not test for these values the impact can be quite drastic on the
experimental variogram, since we are adding artificial (often randomly located)
noise.
136

Ext reme Val ues
We will discuss some approaches to modelling variograms with extreme values
below (e.g. log variograms, relative variograms). However, one particular case is
that where there is a single, very large value in a data set mostly comprised of very
small values. The variogram may be severely impacted by such a value, refer to a
study by Rivoirard (1987a).
Note that, since the richest values often determine the economics of a deposit,
cutting them (or removing them) should be a last resort if we are taking a scientific
approach.
Ot her Approaches t o Cal culat i ng Variograms
In addition to the traditional experimental variogram of grades:
( ) ( ) ( ) { } [ ]
=
+ =
N
i
i i
x Z h x Z
N
h
1
2
2
1

There are a number of other approaches to calculating experimental variograms.
Such approaches fall into two broad categories:
1. Robust estimators of the variogram (e.g. relative variograms).
2. Variography of transforms (e.g. logarithmic and Gaussian variography,
indicators, etc.).
Alt ernat ive Est imat ors of t he Variogram
Alternatives to the calculation of the experimental variogram may perform better in
the presence of extreme values, and in particular for very skewed data. In each case,
the aim of these alternative estimators is to produce a clearer display of the
underlying spatial structure. This structure may be masked in an erratic
experimental variogram.
Robust Est imat ors
Firstly, it should be noted thatin addition to relative variograms (which are
robust in certain cases, as we shall see)robust variogram estimators have been
proposed by Cressie and Hawkins (1980) and several other authors. These
estimators were developed theoretically and intended as alternatives to calculation
of the traditional variogram. They are rarely (if ever) implemented in mining
software. David (1988) gives a review of some alternative estimators.
The traditional variogram and the variations noted below are probably as good as
any of these alternatives if calculated with intelligence and modelled with
experience. Consequently we will not consider these specialised estimators in any
detail.
Out l i er s
Extreme values
disproportionately impact on
the experimental variogram
because the variogram is
calculated by squared
differences.
Seei ng t he
under l yi ng
st r uc t ur e
The underlying structure
may be masked in an erratic
experimental variogram.
Alternative approaches to
variography may
significantly help with this.
137

Rel at i ve Vari ograms
The most commonly encountered robust variograms are relative variograms.
There are several different types of relative variogram and it pays to determine
exactly which one your software is implementing. Relative variograms have been
used for structural analysis and for kriging since the 1970's. They were especially
promoted by Michel David and his students at Montreal (David, 1977, 1988).
The aim of relative variograms is to compensate for the proportional effect. Recall that
a proportional effect exists when there is a relationship between the local mean and
the corresponding local variance.
A proportional effect is the norm with lognormally distributed data and common
in deposits exhibiting skewed (but not necessarily lognormal) histograms. Since
proportional effects are often seen in gold deposits, the use of relative variography
can sometimes provide better resolution of the underlying structure when dealing
with gold data.
Local Rel at i ve Vari ogram
The local relative variogram is a historical way of accounting for the dependence of
( ) h on the local mean. It is rarely used today, because the main motivation of this
approach was limited computer memory in the 1970s.
In this approach, we define regions and treat the data within each region separately,
i.e. as separate populations. If we observe that the shapes of the variograms for
each of our sub regions are similar (only the magnitude or sills differing from
region to region) then we can define a single local relative variogram ( ) h
LR
. This
single relative variogram must then be scaled by the local mean to obtain the local
variogram (Isaaks and Srivastava, 1989):
( )
( )
( )
( )
=
=
=
n
i
i
n
i i
i
i
LR
h N
m
h
h N
h
1
1
2

where the
i
h ( ), i.e.
1 2
( ), ( ),..., ( ) h h h
n
are the variograms for the n local
regions defined, m m m
n 1 1
, ,..., and N h N h N h
n 1 2
( ), ( ),..., ( ) are the
corresponding local means and number of sample pairs from each region. The
above equation thus scales each local variogram by the square of the local mean
then combines them in a weighted average (weighting by the number of sample
pairs upon which each local variogram is defined). The resulting local relative
variogram accounts for a linear-type proportional effect where the local variance is
proportional to the square of the local mean.
Pr opor t i onal
Ef f ec t
The aim of relative
variograms is to compensate
for the proportional effect.
138

If the proportional effect is not linear, an appropriate alternative scaling factor
would need to be built into the above expression.
It's evident that this approach to local variograms can be computationally heavy
(depending upon n) and also that the component local variograms, from which we
build ( ) h
LR
are based upon smaller numbers of samples than the overall data set,
thus reducing the statistical reliability of the resulting combined relative variogram.
In fact, ( ) h
LR
may be little better than ( ) h , depending on how many sub-
populations we are required to define. This approach to relative variography is
consequently not common.
General Rel at i ve Vari ogram
The general relative variogram ( ) h
GR
is a more common relative variogram. It does
not require the definition of sub-populations, overcoming one of the main
difficulties with the approach taken when using the local relative variogram.
For the general relative variogram we calculate (for each lag):
( )
2
)} ( {
) (
h m
h
h
GR
=
where ( ) h is simply the traditional experimental variogram, and m h ( ) is the
mean of all the data values used to estimate ( ) h for the lag h being considered.
The program used to calculate the experimental variogram can be easily modified
to calculate m h ( ) for each lag, so the general relative variogram is easily
implemented from a computational point of view.

Pai r-wi se Rel at i ve Vari ogram
The general relative variogram ( ) h
GR
employs the squared mean of all the data
contributing to a given lag. In contrast to this, the pair-wise relative variogram
( ) h
PR
also uses the square of the mean, but the adjustment is made for each pair
{ ( ), ( )} Z x Z x
i j
considered. Again, this adjustment serves to reduce the impact of
very large values on the calculation of the variogram. The correction made is:
( )
( )
=
2
2
)} ( ) ( {
2
)} ( ) ( {
) ( 2
1
j i
x Z x Z
j i
PR
x Z x Z
h N
h
A note of caution raised by Isaaks and Srivastava (1989) concerning this type of
relative variogram is that when the two data forming the pair both have zero value
(or close to this) their mean is zero, and we divide by zero in the standardisation.
This means that ( ) h
PR
becomes equal to infinity. To avoid this, zero values are
set to a small positive value.
Si gma
2
i -j Rel at i ve Vari ogram
Pr opor t i onal
Ef f ec t (2)
If the proportional effect is
not linear, relative
variograms lose
effectiveness.
139

We may also correct the variogram by the variance of the data contributing to a
given lag. This correction can result in considerable 'cleaning up' of noisy
variograms. The sill is re-set to 1.0.
Some General Comment s About Rel at i ve Vari ograms
The theoretical foundation of relative variograms is not well understood. However,
they have proved very useful in practice. Kriging with a relative variogram, or
performing extension or dispersion variance calculations (see subsequent chapters)
is to be approached cautiously.
In particular, the general relative variogram (which is probably the most common
relative variogram considered) is an estimator, and it often overestimates the
underlying or true relative variogram (David, 1988). In this case, dispersion,
extension and kriging variances obtained from it will also be incorrectly estimated.
However, there is no real difficulty in kriging with a general relative variogram, so
long as we remember that the variances have been rescaled by the square of the
mean (e.g. the kriging variance is now the relative kriging variance).
However, kriging directly with a pair-wise relative variogram is problematic. The
variances are now rescaled in a non-linear manner, and the relative nugget effect is
usually understated (sometimes by a large margin).
Note also that the structures observed in relative variograms can be very helpful in
determining ranges to choose when fitting a model to the conventional
experimental variogram. In the case of gold deposits and other mineralisation with
skewed distributions, the relative variography is usually interesting to calculate (and
not too time consuming) as part of the overall spatial data analysis and structural
modelling step.

Vari ography of Transforms
Before considering a few common transformations, we should be clear about the
implications of some of these approaches. In particular, the user should understand
that:
When we employ a transformation that applies to all the grades, for
example, taking logarithms, we generally alter the variances of the different
structures. This means that we cannot directly determine the relative
nugget effect, or the contribution of a short-range versus a longer-range
spatial structure by direct examination of the variogram based on
transformed values. We will require a back-transform (and this involves
assumptions).
The ranges of structures are generally unaltered by such transformations.
The reason is clear: the distance at which, say, the logarithms of the grades
become uncorrelated is the same as the distance at which the grades
themselves become uncorrelated.
Some common transformations are:
War ni ng!
Kriging directly with a pair-
wise relative variogram is
problematic. The variances are
now rescaled in a non-linear
manner, and the relative
nugget effect is usually
understated.
140

Logari t hmi c Transformat i on
Taking the logarithm of each sample value prior to calculating the variogram can
result in markedly better variography. Note that there is no inference here of
lognormality. This step is just a convenient deskewing transform that helps us to see
the ranges of the structures we are trying to detect. Because the taking of logs
drastically reduces the relative magnitude of extreme values, it reduces the influence
of a small proportion of very high assays on the experimental variogram.
As previously stated, the range is the distance at which sample pairs cease to exhibit
correlation. Taking the logarithm of all the samples does not alter the distance at
which correlation is observed to cease. However, we may see the range clearly in
the log variogram in cases where the experimental variogram of the raw values in
very noisy and thus difficult to interpret.
Note also that in the case of a lognormal distribution, the relative variogram,
traditional variogram and the log variogram are also theoretically equivalent (i.e
there are relationships to convert parameters from one type of variogram to
another see Davids 1988 book).
In general, we will try these different approaches as part of our assessment of
difficult variography and use the information that is gleaned to improve the model
we finally select.
In the case of a lognormal distribution, such a variogram can subsequently be used
for lognormal kriging (although this method is inadvisable when the distribution
deviates much from strict lognormality).
There are a few preliminary steps to be careful of when dealing with logarithmic
variography. First, zero and negative values must be carefully corrected to small
positive values prior to taking logs! Secondly, there is the problem of very small
values.
If we have very small values in our data, then taking logs will result in some quite
large negative logarithms. The squared differences that we use to calculate the
variogram can then become very large. The end result is that we may get a masking
of the underlying structure, or worse, structural artefacts due to these small values.
Rivoirard (1987) gives an excellent case study (for a uranium deposit) where many
grade values were small or below detection, resulting in difficult variography for
even the log values. In this case, he opted to calculate the variogram for a new
variable:
+ x
where is a constant value added to every datum. This results in the differences in
logs being drastically reduced, greatly improving the resolution of spatial structure.
Rivoirard suggests a value for that is close to the mean, or median of the data
set. The value is equivalent to the additive constant for a three-parameter
lognormal distribution.
War ni ng!
Relationships between log
and normal variograms
presume lognormality
141

Gaussi an Transform
A Gaussian transform (or anamorphosis) is a transformation of the data that
results in a normal histogram. In the case of a lognormal distribution, taking the
logarithms results in a Gaussian (or normal) distribution. Therefore, for a
lognormal distribution, taking logarithms is a Gaussian transform. In the general case,
a Gaussian transform can be made for any unimodal distribution.
Again, no inference of normality is made: the Gaussian transform is simply a
convenient deskewing to allow us to see obscured spatial structureit can't create
structure that isn't there! In fact, transforms like Gaussian and log can be viewed as
data filters. The usual Gaussian transform results in the data values having a
histogram of a standard normal distribution, i.e. with a mean equal to 0 and a
variance of 1.0. Consequently, the sill of the variogram of Gaussian transformed
data will be at 1.0.
Journel and Huijbregts (1978) and Hohn (1988) give full details on Gaussian
transformations. There are two ways to do this: first, graphically (figure 6.12) and
secondly by Hermite polynomial expansion. This latter method is equivalent to the
first, but more mathematically useful. The details of Hermitian Gaussian
transforms are beyond the scope of this course. In summary, the Hermite
polynomials are a convenient series of functions that, when added together, can
approximate most functional shapes. The transform is:
n
n
N
n
n
H y
!
( )
=
1

Figure 6.12 Graphical Gaussian transformation (anamorphosis) after Journel and Huijbregts (1978)
Note that, under certain assumptions, the variances of each structure in a model for
a logarithmic or Gaussian variogram can be related to the variances in the
traditional variogram, making these models useful for determining the nugget effect
and sills as well as the ranges. In the case of the Gaussian transform, this
relationship is given by Guibal (1987) as:

Z
n
n
N
Y
n
h
n
h ( )
!
{ ( )} =
=
2
1
1 1
Nor mal i sat i on
A Gaussian transform is
simply a transformation of
data to a normal
distribution: a standard
statistical tool.
142

where
Z
h ( ) is the variogram in terms of the Z (or raw) values, and
Y
h ( ) is the
variogram of the Gaussian transformed values. If the Gaussian transform is
available, it is generally preferred to using logs and usually performs better. This is
because the log transform will not generally result in a Gaussian distributionthis
will occur only if the data are strictly lognormally distributed (and this is very rare).
I ndi cat or Transforms
The use of indicators is a different strategy for performing structural analysis with a
view to characterising the spatial distribution of grades. In this case, the
transformed distribution is binary, and so by definition does not contain extreme values.
Furthermore, the indicator variogram for a specified cut off z
c
is physically
interpretable as characterising the spatial continuity of samples with grades
exceeding z
c
.
A good survey of the indicator approach can be found in the papers of Andre
Journel (eg. 1983, 1987, 1989).
An indicator random variable I x z
c
( , ) is defined, at a location x, for the cut off
z
c
as the binary or step function that assumes the value 0 or 1 under the following
conditions:
I x z Z x z
I x z Z x z
c c
c c
( , ) ( )
( , ) ( )
=
= >
0
1
if
if

After transforming the data, the indicator variogram can be calculated easily by any
program written to calculate an experimental variogram. An indicator variogram is
simply the variogram of the indicators.
In addition to its uses for indicator kriging (IK), probability kriging (PK) and allied
techniques, the indicator variogram can be useful when making structural analysis
to determine the average dimensions of mineralised pods at different cut offs, for
example.
We now consider the application of some of these techniques for structural analysis
of a gold deposit.
A Case St udy of Variography
The following study (Vann, 1993) was designed to characterise spatial distribution
of the known primary ore in an open pit gold mine
The aim of the study was to guide subsequent analysis of future exploration drilling
strategies and estimation methodologies. However, the overall approach gives an
example of the process of making a structural analysis.

I ndi c at or s
Indicator transformations
are non-linear. Thus we
cannot krige untransformed
grades using indicator
variograms, including the
median indicator variogram.
143

The Dat a
Grade control at the mine was performed by kriging. The kriging was based on
gold fire assay results from sampling of vertical, 5m deep blast holes (BH). The raw
BH data is the most exhaustive grade information available for the mine.
The initial step of the study was to flag data within the zone of geological interest.
BH holes were mostly drilled on 3 x 8 m spacings but some areas were drilled at 3
x 4 m. Holes that were not on the 3 x 8 m pattern were excluded. This step is a
declustering and was necessary to avoid preferential (or clustered) sampling which
may affect statistics and variography.
Advant ages of Consi st ent Spaci ng
Another reason that a consistent sampling pattern is desirable is that it enables us
to construct a block model in which, on average, each cell contains only one BH
sample. This is useful if meaningful conditional statistics are to be calculated and
also has considerable advantages from a viewpoint of computational efficiency
when calculating variograms.

Figure 6.13 Example of sample locations (declustered)
144

Hi st ogram
The histogram is given in figure 6.14.

Figure 6.14 Histogram of the BH gold assays (declustered)
Notes:
The coefficient of variation (CV) or relative standard deviation exceeds
2.0.
The histogram is asymmetrical, with a clear positive skewness, i.e. it is
skewed to the right, with a tail of high values.
The mean exceeds the median by approximately 1.0 g/t.
The data include some values that are extreme in the sense that they are
very high (e.g. the 115 g/t assay).
The above observations indicate that it will be difficult to perform estimations for
this mineralisation. The presence of a small percentage of high grades, implied by
the skewed distribution, is often a forewarning of noisy grade variograms. A few
very high values can have a large influence on an experimental variogram
(Rivoirard, 1987a).
145

Deposits with CV's well in excess of 1.0 (gold and uranium deposits, for example)
are often difficult from the point of view of variography and estimation (Isaaks and
Srivastava, 1989).
Proport i onal Ef fect
Previously we learned that a proportional effect is present when the local variance is
proportional to the local mean. Lognormal distributions always exhibit a
proportional effect, for example.
Figure 6.15 shows plots of variance (s
2
) versus squared mean (m
2
) for columns,
rows and benches in the block model. Plotting standard deviation (s) versus mean
(m) is, of course, equivalent. A proportional effect is present since the variance of
the grades in a column/row/bench systematically increases with the mean grade of
that column/row/bench.

Figure 6.15 Plots of proportional effects
Hi gh CV
A high CV (say > 2.0) is an
indication that variography
will be difficult.
146

We note that he proportional effect observed is not strictly linear, with some
suggestion of at least a component of the proportional effect being quadratic in
nature.
Vari ograms
The variogram enables us to characterise the spatial distribution (or continuity) of
mineralisation for interpretative purposes, in addition to providing a structural
function for kriging. The aim of variography in this study was to attempt to
characterise the mineralisation, especially with respect to the distribution of high
grade material.

Figure 6.16 Experimental variograms
The BH composites, being at the nodes of a block model, are regularly spaced, at 8
metre intervals in the north-south (Y) direction, 3 metre intervals in the east-west
(X) direction and 5m intervals in the vertical (Z) direction. Calculation of the
variogram is straightforward for regularly spaced data and (as discussed earlier).
The definition of appropriate lag spacings is simple in such a case: lags are chosen
that correspond to the dimensions of a unit cell in the block model.
Figure 6.16 shows directional experimental variograms calculated for the zone of
interest. The variance (s
2
) of the BH data is indicated on figure 6.16 (and
subsequent figures) by a dashed line.
For the sake of clarity, only the experimental variograms calculated for the principal
directions of the block model are shown. The intermediate directions (NW-SE and
147

NE-SW), although calculated in each case, cluttered these plots unnecessarily and
are therefore not shown.
The experimental variogram suggests a high relative nugget effect (); i.e. the
experimental plots, if extrapolated to the ( ) h axis would intersect at a level close
to that of the variance of BH samples (a priori variance = 12.3).
The variogram in the EW direction reveals a single spatial structure with an
apparent range of about 15-20 metres. The fall in ( ) h at lags beyond 40m in the
EW direction is mainly due to the progressively smaller number of pairs employed
to calculate ( ) h at these lags. Recall that an experimental variogram cannot be
considered strictly reliable for distances beyond one third of the maximum
available lag spacing.
Possi bl e Non-St at i onari t y?
The variogram in the vertical direction is structured but does not reach a sill. Points
beyond the 30m plotted in figure 6.16 continue to rise, but are based, as with the
distal lags of the EW variogram, on too few sample pairs to be regarded as reliable.
It was known that an increasing trend in grade existed for the lowermost benches
of the zone of interest and this possible non-stationarity might provide an
explanation for the observed variogram behaviour in the vertical direction.
The variogram in the NS direction rises up to a distance of about 50-60 metres and
then stabilises at about the level of the a priori variance.
Given the presence of proportional effects, discussed above, relative variograms
would be expected to be more structured than the nave variogram (i.e. as
calculated above).
Pai r-Wi se Rel at i ve Vari ogram
There are a number of different ways of calculating relative variograms (see David,
1988, pp.42-49 and Isaaks and Srivastava, pp.163-170 for details). The use of
relative variograms was pioneered by David, and although their theoretical
applicability has been debated, they can be very useful tools to reveal structuring in
data sets where variography is influenced by very high values. The particular
relative variogram employed here is a pair-wise relative variogram ( ) h
PR

standardised by lag variance, introduced as the Sigma i-j relative variogram in the
previous section of this chapter.
The experimental relative variogram still suggests a high relative nugget
effect () though possibly lower than the raw variogram.
In the EW direction there is a short-scale structure with an apparent range
of about 15-20 metres. Also evident is a possible longer-scale structure
with a range of 30-40m or so. The fall in ( ) h at lags beyond 40m seen in
the variogram is not observed in the relative variogram.
Rel at i ve
Var i ogr ams
In the case of a linear
proportional effect, a relative
variogram should work
well.
148

The relative variogram in the vertical direction also rises without reaching
a sill.

Figure 6.17 Relative Variogram (Sigma i-j)
The relative variogram in the NS direction has an inflection at the second
lag that is suggestive of a short-range structure. This inflection is only
subtly evident in the traditional variogram, and is better revealed by
the( ) h
PR
plot. The longer-range structure seen in the variogram is also
clearer in the relative variogram, with an apparent range of perhaps 100
metres.
Vari ograms of t he Logari t hmi c Transf orm
The stated purpose of this variography was to characterise spatial distribution of
mineralisation, especially the average shape and dimensions of high grade pods of
ore. In this context then, it is the ranges, and more specifically, the anisotropies,
from the variography that interest us. Given the skewed nature of the BH
histogram, it was decided that employing transformations of the data would better
assess these.

149

Ext reme Val ues & Vari ography
Highly skewed histograms containing extreme valued observations
19
are usually an
early warning of poor variography of the raw grades (in this case, untransformed
BH composites). Extreme values are the richest samples, and in the case of gold
deposits can make the orebody economic. To remove (or cut) the extreme values in order to
improve the variography is dangerous indeed!
To deal with the problem of describing spatial continuity of strongly skewed
distributions that include extreme values, one alternative is to employ relative
variograms, another strategy is to use some transform of the original values.
For example, rather than simply calculate variograms of the original data values,
variograms of their logarithms may be calculated.
The Impl i cat i ons of t he Transform
We repeat that the use of a logarithmic transform does not imply any assumption of
underlying lognormality of the distribution. In any event, few mineral deposits have
truly lognormal distributions. The logarithmic transform is simply a convenient
deskewing transformation that reduces the adverse effects of very high values on
the variography.
Another common approach is to transform the distribution to that of a normal
distribution, i.e. the Gaussian transformation. The log transform is used here for
reasons of simplicity, not for any theoretical reason. In fact, since the BH data are
more skewed than lognormal, a Gaussian transform may have performed even
better.
By reducing the skewness of the distribution using any such transform, more
structured, interpretable variography can often be obtained. The particular
deskewing transform employed used here is a variation on the simple logarithmic
transform:
z x a z x '( ) log{ ( )} = +
This form of log transform endeavours to avoid amplifying small differences
between low values by adding a translation constant a to each observation prior to
taking logarithms. The value of a is equivalent to the additive constant for the three
parameter lognormal distribution. It should be specified bearing in mind the order
of magnitude of the values themselves (Rivoirard, 1987a). In this case a value of
1.0, a value falling in between the median and mean values of the BH data, was

19
The term outlier is used in classical statistics to imply that data are outside some limits, beyond which
values are considered uncharacteristic (see Velleman and Hoaglin, 1981, p.67). Because of this, the term
outlier should be used with care when dealing with populations of gold assays. The term extreme value is
preferred. Closer spaced observations may place such extreme values in context with surrounding values,
so terms like erratic value should also be used with care. As used here, the label extreme simply means a
high-valued observation that has an undue influence upon experimental variography. An extreme value
may be an observational or other error, and consequently, such high values should always be examined
carefully. If such values are legitimate, they make a disproportionate contribution to the metal content of
the deposit and it is inadvisable to employ arbitrary cuts.
Ex t r eme val ues
Removing (or cutting) the
extreme values in order to
improve the variography is
dangerous indeed!
150

added. The variogram ( ) h
L
of the transformed data set is then simply calculated.
The resultant directional experimental log variograms are shown in figure 6.18.

Figure 6.18 Variogram of logarithmic transform

The Model Fit t ed
A nested spherical model was fitted. This model is of the form:
( ) ( ) ( ) h C C Sph a C Sph a = + +
0 1 1 1 2 2 2

Where Sph denotes the spherical variogram model and C
0
, C and a
represent the nugget, sill and range respectively. The parameters of the model are
tabulated on figure 6.18.
Log Vari ograms and Rel at i ve Vari ograms
The logarithmic variogram of the BH data is certainly more clearly structured than
the relative variogram. David (1988) notes that:
151

a logarithmic (semi-) variogram ( ) h
L
usually looks better than a relative
(semi-) variogram ( ) h
PR
computed on the same data, hence it is easier to fit
a model to the logarithmic (semi-) variogram.
Note that a relation exists for converting the model derived from the log variogram
to that of the relative variogram, and that the two are equivalent in the case of
lognormality (see David, 1988 for details).
The range for a variogram or relative variogram should be the same as that for a
log variogram on the same data. This is because if two values are independent of
each other, then so are their logarithms. The better-defined, continuous structure
revealed in the log variogram is a result of reducing the influence of extreme values
by employing a deskewing transform. This underlying structuring is virtually masked
in the "naive" variogram, and not even revealed very well in the relative variogram.
The Rel at i ve Nugget Effect and Non-Li near Transformat i ons
The apparent relative nugget effect () is much lower on the log variogram.
Warning: unlike the range, the ratio C C
0
/ changes when non-linear transform is
employed (like taking logarithms)! It can be shown from theory that this ratio is
always higher in the relative variogram than it is in the logarithmic variogram.
The larger relative nugget effect in the variogram and relative variogram compared
to the log variogram is explained by stronger short-scale variation in grade when
considering real grades as opposed to log-transformed grades (David, 1988). The
use here of an additive constant in the log transform enhances the effect, further
decreasing .
Ranges
The model fitted has a NS range of 150m, although the experimental variogram in
this direction levels out at about 110m before a slight rise at a higher level at about
140m. It seems reasonable to say that the long-scale structure in the NS direction
has a range of between 110-150m. The important short-scale NS structure
observed previously in the relative variogram is also clear here, with a range of
20m.
Ani sot ropy
There is pronounced anisotropy, with the EW log variogram presenting much
shorter ranges than those observed in the NS direction
20
. However, the
experimental log variogram in the EW direction has an undulating form: it starts to
level out at 15m or so, only to rise sharply again to stabilise at the level of the sill.
A more subtle behaviour of this type is also apparent in the NESW direction (at
about 50-60m). A possible explanation is that the mineralisation is more strongly
heterogeneous in these directions; in other words, we are dealing with non-

20
The anisotropy here is specified by anisotropy ratios. The model in the NS direction (the longest range in
all cases) is assigned anisotropy ratios (Y-anis in the figures) of 1.0 for Sph1 and Sph2. The spherical
structures in the other directions must be divided by their anisotropy ratios (X-anis and Z-anis) to obtain
the ranges discussed in the text).
Rel at i ve Nugget
Unlike the range, the relative
nugget effect changes when
non-linear transform is
employed.
152

stationary behaviour. The long-range in the EW direction is estimated to be 30m
while the short-scale structure has a range of 13-15m. The subject of the "poddy"
nature of the mineralisation discussed further, below.
The experimental log variogram in the vertical direction is incomplete: there are not
enough lags in this direction to define it properly. There is no way around this
problem; it is a limitation of the available data. The model finally fitted assumes a
nested spherical structure with a short range of approximately 13-15m (i.e. the
same as for the EW direction) and a longer range of about 40m (i.e. slightly longer
than in the EW direction).
Because of the availability of only 10 lags (ten benches, a distance of 50m) for the
experimental variogram in the vertical direction, specification of the long range is
particularly uncertain.
The experimental log variograms for the NESW & NWSE directions have
intermediate ranges. This is consistent with the long-axis of the anisotropy ellipse
(in the horizontal plane) being oriented NS and the short-axis EW.
The ranges of the log variogram are thus consistent with an overall, or large-scale,
control on the mineralisation on a scale of 100-150m NS and 30m EW, i.e.
pronounced anisotropy is evident. Any large-scale control on mineralisation
geometry in the vertical direction cannot be determined with the available data.
Short-scale structures have ranges of about 15m-20m in NS, EW and vertical
directions; i.e. the short-scale structuring is effectively isotropic.
Agai n: Possi bl e Non-St at i onari t y?
It is worth noting that the log variogram in the vertical direction does not rise above
the level of the overall variance in the manner it did for the conventional variogram
and the relative variogram. The smoothing transform of taking logs has eliminated
this artefact, suggesting that it was caused, in part, by a small number of pairs
containing extreme values in the vertical direction, yielding much greater average
squared differences at given lags than in other directions.
At greater lags, there are always fewer pairs, and the impact of a single high value
will become more pronounced as the number of pairs falls. The behaviour of the
experimental variogram in the vertical direction implies that extreme values occur
near the top or bottom of the zone of interest. In fact, the two richest samples (115
and 99 g/t) occur on the lowermost two benches of the zone of interest. The trend
for increasing grade on the lowermost benches of the zone of interest is real, but is
probably exaggerated by a few very high grades.
Vari ograms of t he Indi cat or Transform
For an indicator transform, each sample is assigned a value of 1 or 0 depending upon
whether or not it exceeds a specified cut-off, z
c
.
Why Use Indi cat ors?
153

The use of indicators is a different strategy for performing structural analysis with a
view to characterising the spatial distribution of grades. In this case, the
transformed distribution is binary, and soby definitiondoes not contain extreme
values. Furthermore, the indicator variogram for a specified cut off z
c
should be
physically interpretable as characterising the spatial continuity of samples with
grades exceeding z
c
.
S EL ECT I NG T HE CUT OF F
Indicator variograms were calculated for the indicator ) 0 . 3 ( =
c
z I . This cut off
was selected after producing and examining bench-by-bench 1:500 scale hand
contouring of raw BH data for the entire zone of interest (not reproduced here).
These data for these plans were generated by computer and then broadly
contoured by eye at several cut offs. This suggested coherence of mineralised
pods at cut offs up to about 5 g/t, but destructuring
21
above this cut off. The 3 g/t
cut off showed the most coherent outlining of higher grades.
Lower cut offs were used to extend the analysis. In this case, we will only present a
single cut off.
Figure 6.19 shows the I z
c
( . ) = 30 variogram for the principle directions of the
block model, i.e. the EW, NS and vertical directions. The experimental indicator
variogram for the intermediate directions (NWSE and NESW) are not shown,
again for the sake of claritythey fall between the NS variogram and the shorter-
range EW and vertical variograms, as was the case for the log variogram.

21
Destructuring of high grades is a phenomenon described by Matheron (1982) in which the indicator
variograms for progressively higher cut offs tend towards a pure nugget effect model.
Ex t r eme Val ues
The indicator-transformed
distribution is binary, and
soby definitiondoes not
contain extreme values.
154

Figure 6.19 Variogram of indicator for cut off = 3.0 g/t
An anisotropic, nested spherical model with nugget effect is once again fitted.
Points to note:
The relative nugget effect is, again, lower than for the variogram and
relative variogram.
The long range in the NS direction is about 80m and the short range is
20m.
The model fitted for the EW and vertical directions is identical for the
I z
c
( . ) = 30 variogram. Both directions present short-scale structure with
a range of about 6-7m and a long range of 20m.
S HOR T R ANGE S T RUC T UR ES
The short-range structures in the NS, EW and vertical directions strongly suggest
the presence of coherent +3g/t mineralised pods, of no overall preferred
orientation, with average dimensions of about 15-20m. The long-range structure in
the NS direction probably reflects the overall geometry of the mineralised zone.
155

Overall, the indicator variography for I z
c
( . ) = 30 reinforces the picture obtained
from the log variogram, above.
Summary of Vari ography
The aim of this variography was to attempt to characterise primary mineralisation,
especially with respect to the distribution of high-grade material.
Vari ograms
The variogram of the raw or untransformed BH data is only poorly structured.
From the point of view of characterising the shape of high-grade pods of
mineralisation it is not very useful. A large relative nugget effect () was observed.
The influence of a small proportion extreme-valued data on the variogram was
pronounced.
The pair-wise relative sigma i-j variogram gives a clearer picture of the distribution
of grade in the zone of interest. This is no doubt due to the presence of a distinct
proportional effect. In such situations relative variograms are more robust and
usually perform better than nave or raw variograms. A discernible anisotropy
was observed in the relative variogram.
Log Vari ograms
Variography for a log transform gave the clearest picture of the structuring of
grade. In addition to clearly revealing anisotropy, the log transform enabled the
fitting of a nested spherical model. We would expect a similar picture to emerge
from a structural analysis based on a normal (Gaussian) transform.
I ndi cat or Vari ograms
Indicator I(3.0) transform was chosen on the basis of grade maps. At a 3.0 g/t cut
off there is clear structure in the indicator variogram. This is physically interpretable
as summarising spatial continuity of mineralisation above this grade.
Charact eri sat i on of Spat i al Grade Di st ribut i on
The variography thus gave us the following picture of spatial distribution (or
character) of gold grade:
Long-range structures, corresponding to overall control of mineralisation,
have ranges of 100-150m NS and 30m EW, i.e.: pronounced anisotropy.
Short-range structures, corresponding to high grade pods, have ranges of
15-20m in both NS and EW directions. Indicator variography supports
this interpretation of isotropy for +3 g/t pods.
Vertical ranges are at least 15m. Only 50m of vertical BH data was
available; beyond about one third of this distance (17m) interpretation of
variography is tentative.

156

Geol ogical Fact ors
Geological interpretation is a vital and parallel step to variographic and statistical
analysis. The overall model should be obtained as a result of performing and
comparing all three analyses.
As an adjunct to the variography and exploratory data analysis performed for this
study, a comprehensive and complete sectional, level-plan and long-sectional
geological interpretation of the zone of interest was made. An attempt was made to
integrate grade control data with diamond drilling information and in-pit geological
bench mapping. The interpretation produced was thus based on all the available
BH, DDH and mapping data within the zone of interest.
This interpretation was largely made possible by computerised production of
coloured BH grade plots in cross-section, plan and long-section. Importantly, pit
mapping and DDH information only revealed a partial picture of the mineralisation:
BH data was essential to allow detailed characterisation of high-grade pods.
Compari son of Geol ogy and Vari ography
This step is compulsory! In our case, geological interpretation compares well with
variography, showing major NW-trending structures at 100-150m (NS) spacing
and NE-trending structures at ~30m (EW) spacing, giving a physical explanation
for the observed variography. High grade pods average about 20 m x 20 m in plan
and show no clear-cut overall anisotropy, although some individual pods may be
elongated NS, EW or obliquely.

C H 7 S U P P O R T
157

Support
This problem of the discrepancy between the support of our
samples and the intended support of our estimates is one of the
most difficult we face in estimation.
Ed Isaaks and Mohan Srivastava An Introduction to
Applied Geostatistics 1989
What is Support ?
Often a regionalised variable (ReV) is defined on a surface or volume rather than on a
point. While it may be sensible to consider an elevation to be defined at a point, we
usually consider grades to be associated with a volume. The basic volume upon
which a ReV is defined or measured is called the support of the ReV. Complete
specification of support includes the shape, size and orientation of the volume
(Olea, 1991).
If we consider the same phenomena (say gold grades) with different support (say
1m cores versus 2m cores) then we are considering two different ReV's. These two
ReV's have different support and this implies different structural (or variographic)
character. Grades defined on RC chip samples, HQ cores, underground channel
samples, and mining blocks will thus be distinctly different in character.
So, the important question arises; how can we relate ReV's defined on different
supports? Another way to phrase this is: knowing the grades of cores, what can
we say about the grades of blocks?
We will consider the answer to this important question in two stages. Firstly, we
consider the dispersion as a function of support.
Chapter
7
Def i ni t i on
The basic volume upon
which a grade (or other
spatial variable) is defined or
measured is called the support
of that variable.
C H 7 S U P P O R T
158

"Dispersion" as a Funct ion of Support
Grades measured on a small support, say core samples v, can be much richer or
poorer than grades of the same mineralisation that have been measured on larger
supports, say mining blocks V=5x5x5m. Statistically, we say that grades on sample
support are more dispersed than grades on block support.
Support Effect
In general, grades on smaller supports are more dispersed than grades on larger
supports. Although the global mean grade on different supports at zero cut-off
should be identical, the variance of smaller supports will be higher. Support effect
is this influence of the support on the distribution of grades.
An Exampl e
We will consider the idea of dispersion via an example originally given by Delfiner
(1979). The data are porosity measurements made on a thin section of sandstone,
but they could be viewed as grades or any other additive attribute: the principles
involved will not change. It may seem strange to work at such a small scale, but this
allows us to obtain exhaustive datanot usually accessible in most geostatistical
applications.
The sandstone thin section was divided into 324 contiguous square areas, each
square having sides 800 microns long (1 micron = 10
-6
metres). Table 7.1 shows
the original data.
Porosity values were then averaged by groups of 4 (2x2 blocks); groups of 9 (3x3
blocks); and groups of 36 (6x6 blocks). The results of these averaging steps are
given in tables 7.2, 7.3 and 7.4. Each table represents the same area.
C H 7 S U P P O R T
159

Table 7.1 Porosity Data - Original Measures Values
20.18 20.42 24.43 25.67 26.05 21.22 18.17 21.14 27.43 19.46 20.57 8.77 7.53 15.19 24.11 28.58 29.83 23.80
19.37 13.94 21.62 20.02 11.93 6.81 18.46 19.38 23.27 29.30 25.06 22.40 29.84 25.10 21.57 29.11 26.57 17.72
20.92 23.60 18.81 16.29 25.20 20.13 22.33 20.91 24.68 26.30 20.75 22.14 19.20 19.54 20.80 13.94 20.41 19.26
28.45 22.61 24.70 15.96 25.34 21.50 25.61 29.23 23.91 35.63 33.76 21.58 21.27 24.37 23.35 16.43 25.33 20.10
22.82 22.29 16.97 26.87 27.28 19.51 25.37 28.08 15.49 17.23 24.70 29.04 22.93 31.76 18.63 22.29 27.55 29.51
22.32 25.64 21.35 24.68 21.39 21.75 21.59 31.30 33.57 21.99 22.78 25.95 26.10 26.34 37.22 27.03 15.09 18.41
20.96 19.89 24.44 29.59 25.34 32.10 22.48 28.12 23.34 24.15 27.42 18.49 28.17 21.38 21.46 29.95 26.31 33.14
21.93 23.48 22.76 24.46 22.16 30.37 26.43 28.07 28.11 30.80 25.72 28.99 25.85 26.76 18.87 25.18 22.15 26.72
14.02 19.59 21.03 23.60 26.17 22.20 15.83 17.65 29.48 24.75 36.27 24.07 23.55 25.54 32.82 24.33 33.79 25.93
27.89 28.26 25.10 25.75 22.47 24.36 28.27 22.53 22.72 19.53 26.30 22.50 26.21 23.33 16.53 21.56 16.36 22.02
13.60 21.14 17.65 23.84 21.69 23.70 17.89 24.50 18.42 16.51 23.18 30.37 22.86 19.47 24.93 17.45 25.35 25.95
23.68 23.33 15.96 29.98 9.34 26.86 29.14 30.63 26.94 22.04 22.30 25.44 21.48 16.35 13.96 26.38 17.60 23.71
14.96 20.84 20.50 22.79 22.88 20.51 25.65 24.79 24.84 23.54 21.98 23.22 25.66 21.05 21.63 23.72 25.04 23.28
20.75 26.58 21.19 18.45 20.37 23.68 27.81 23.39 21.47 19.91 26.44 19.10 22.02 12.16 15.31 23.14 16.10 23.56
25.98 20.66 19.98 17.78 20.43 24.15 23.35 27.11 29.51 26.72 19.91 26.53 24.48 21.95 23.15 25.51 24.52 21.41
21.30 27.13 25.13 19.37 19.48 24.01 29.95 21.98 21.70 20.58 26.63 18.37 16.28 23.87 21.37 14.45 19.19 20.32
19.36 22.50 22.22 6.63 19.12 18.72 27.77 22.45 26.15 26.20 21.63 27.89 21.44 19.46 19.30 26.82 26.85 20.65
20.45 24.61 22.43 26.00 23.88 25.60 24.64 25.50 25.92 23.45 21.35 17.73 19.45 15.85 9.75 21.03 17.38 15.44
C H 7 S U P P O R T
160

Table 7.2 Porosities of 2x2 Blocks
18.63 22.93 16.50 19.29 24.86 19.20 19.41 25.84 24.48
23.89 18.94 23.04 24.52 27.63 24.56 21.09 18.68 21.27
23.27 22.47 22.48 26.58 22.07 25.62 26.79 25.84 22.64
21.56 25.31 27.49 26.27 26.60 25.15 25.54 23.86 27.08
22.44 23.87 23.81 21.07 21.14 27.25 24.65 23.81 24.54
20.54 21.86 20.40 25.54 20.98 25.32 22.54 20.68 23.15
20.78 20.73 21.86 25.41 22.44 22.68 20.22 20.96 21.99
21.27 20.56 22.02 25.60 24.10 22.61 21.64 21.12 21.36
21.73 19.32 21.83 25.09 25.43 22.14 19.05 16.67 20.08

Table 7.3
Porosities of 3x3 Blocks
20.44 19.48 21.75 21.64 20.32 23.25
23.02 22.70 26.02 25.85 25.80 22.41
20.90 26.22 24.39 26.74 24.93 27.50
21.89 23.11 24.56 23.13 21.68 21.82
20.16 21.23 25.31 22.70 20.82 22.92
22.79 20.31 25.12 22.64 18.50 19.13
C H 7 S U P P O R T
161

Table 7.4
Porosities of
6x6 Blocks
21.35 23.81 22.95
23.03 24.70 23.98
21.12 23.95 20.34

Note that we observe very high (>30) and very low (<10) values in table 7.1 (the
un-aggregated data), but such extreme values cannot be found in the 2x2 blocks
(tables 7.2-7.4). Clearly, the smallest and largest values are averaged out
(smoothed) as we increase the scale of aggregation. The 6x6 values are quite
smoothed, falling entirely within the range 20-25.
Histograms of the original data and the aggregated data (i.e. 2x2, 3x3 and 6x6
blocks) are shown in figures 7.1, 7.2 and 7.3. We observe that the mean of each
histogram is the samethis makes sense, simply averaging the data into blocks
doesn't alter the mean. However, the dispersions decrease sharply as the size of the
block averaging increases.
As discussed previously, dispersion can be measured in a variety of ways, for
example we can use the range (the difference between the minimum and maximum
value). The ranges pertaining to the different supports we considered are tabulated
below:
Table 7.5: Dispersion of Porosities Measured by Range
Minimum Value Maximum Value Range
Original Data 6.63 37.22 30.59
2x2 16.50 27.63 11.13
3x3 18.50 27.50 9.00
6x6 20.34 24.70 4.36

The variance is another measure of dispersion and is more conventionally used in
statistics and geostatistics. The corresponding variances (in units of 10
-4
) are
tabulated in table 7.6.
Suppor t
When we increase the
support size, the global
mean is unchanged, but the
dispersion is reduced.
C H 7 S U P P O R T
162

Figures 7.1, 7.2 & 7.3 Histograms of porosities: original data, 2x2 and 3x3 averaging

C H 7 S U P P O R T
163

Table 7.6: Dispersion of Porosities Measured by
Variance
Variance
Original Data 22.31
2x2 6.42
3x3 5.11
6x6 1.99

How Geost at ist ics Can Help
We introduced this example by pointing out that the porosities constituted a
relatively exhaustive data set. Of course, if we didn't have all 324 close spaced
porosity measurements, we couldn't calculate the variances presented in the above
tableor could we? Geostatistics allows us to theoretically determine variances on
different supports if we have an adequate variogram model and appropriate tables
(or more commonly these days, a computer program).
The Impact for Mining Appli cat i ons
Clearly, if our example values were grades, then applying a cut off on one support
will give very different results than applying the same cut off on another support. In
fact, recall that figure 1.5 shows that we always predict more ore when using
smaller supports if the cut off if higher than the mean. This makes sense: as we
smooth the grades by using larger supports, there are fewer very high grades.
The practical impact of this is criticalif we are selecting blocks as waste or ore
relative to a cut off, but making this allocation on the basis of drill samples (which
clearly have a very much smaller support than any feasible mining block) then we
will run the risk of seriously overestimating the percentage of blocks over a
given cut off grade.
This problem is inherent in classical estimators, because they can take no account of
support. This is a primary reason why polygonal estimators, for example, require
cutting of high grades to obtain reasonable results.
Note also, because dispersionand in particular varianceis clearly related to
support, we expect the variogram to be different for different supports. This is
because, at the very least, the value of the sill (nominally equal to the a priori
variance) should be smaller for a larger support.
C H 7 S U P P O R T
164

Variances of Dispersion Within a Volume V
Now we have a feel for the impact of support on variance from a simple example,
in summary: the larger the supportthe smaller the variance.
Vari ance of a Poi nt Wi t hi n V
For convenience, we will refer to the supports we consider here as V and v
(representing the larger and smaller supports respectively)
22
.
Under the geostatistical model (of regionalised variables) the variable we study is
viewed as a realisation z(x) of a random function (or RF) denoted Z(x). If we had
all the values of z(x) over a domain V, then we could compute the mean and
variance of z(x) within V. We can denote the mean and variance by spatial
integrals. These can be simply read as being infinitesimal summations:
{ }
=
=
V
V
V
V
dx m x z
V
V o D
dx x z
V
m
2 2
) (
1
) | (
) (
1

where D o V
2
( | ) denotes the variance of points ( o ) within a volume V. For our
purposes a point corresponds to something with zero volume.
It can be shown that this dispersion variance D o V
2
( | ) is equal to average value of
the variogram between two points x and x', when these two points are
independently moved to occupy all the points within a block of size V. The mean
variogram within a block is usually denoted ( , ) V V we read 'bar gamma V V'.
This value is also called the F-Function, and it is graphed in early geostatistical books
for simple variogram models.
Today ( , ) V V can be conveniently obtained via computer programs:
( , ) ( | ) ( ) V V D o V F V = =
2

Interestingly, most commercial software that includes kriging routines still cannot
calculate these useful functions, even though their implementation is simple.
Vari ance of v Wi t hin V
Suppose now that, rather than considering a point support o, we consider a volume
v and the ReV defined on this support, Z x
v
( ). We are interested in the dispersion
of ) (x Z
v
when it is moved within a larger domain V.
For example, v might be a 1m long core sample and V might be a longer core
sample, or a 10m x 10m block (or the whole deposit).

22
When working in 2D V and v would relate to areas rather than volumes.
Cal c ul us
Geostatisticians are naturally
fond of calculus. For those
who arent, all the average
integrals encountered can be
thought of as summations.
C H 7 S U P P O R T
165

The variance of a smaller volume v within a larger volume V is denoted
D v V
2
( | )and it's equal to:
{ }
) ( ) (
) , ( ) , (
) (
1
) (
1
) (
1
) | (
2 2
2 2
v F V F
v v V V
dxdy x x
v
dxdy x x
V
dx m x Z
V
E V v D
v V
V
V V
=
=
=

This result is very interesting, because it allows us to determine the variance of one
support given another. This result is known as Krige's Relationship or sometimes
Krige's Additivity Relationship. It expresses what's commonly referred to as the
volume variance relationship.
Krige's Relat ionship
The results obtained above can be restated here:
D v V D o V D o v
2 2 2
( | ) ( | ) ( | ) =
If V is the whole deposit, for example, and v are mining blocks, and we consider
the cores to be approaching point support, then this expression simply states that:

The variance of blocks in the deposit
is equal to
the variance of cores in the deposit - the variance
of cores within a block
We can re-write this relationship in an additive form, more familiar from
conventional ANOVA (analysis of variance):
D o V D o v D v V
2 2 2
( | ) ( | ) ( | ) = +
This now tells us that the variance of cores in the deposit is equal to the variance
of cores within a block plus the variance of blocks within the deposit. Note that
the variance of points (or the smallest available support, say 1m cores) in the
deposit must be greater than the variance of larger supports within the deposit, i.e.:
Vol ume-Var i anc e
This is referred to here as
Kriges Relationship
C H 7 S U P P O R T
166

D cores deposit D blocks deposit
2 2
( | ) ( | ) >
We will not detail the calculation of F functions or use of charts here, since in most
cases geostatisticians now use computer programs. Refer to Journel and Huijbregts
(1978) or David (1977) for charts and further details.
Change of Support Regularisat ion
Using Krige's Relationship we can now deduce the variance of blocks from the
variance of points (or cores).
Geostatisticians refer to the process of deriving a larger support from a smaller
support as regularisation. A simple example is the act of compositing 1m core
samples into 2m core samples. As a result of regularisation, we expect the grades of
the larger support to be less dispersed. We already know that the ReV defined on
small supports is different that defined on large supports. How can we determine
the variogram of, say, blocks from that of points?
Regul ari sat i on of t he Vari ogram
It can be shown that the variogram of a regularised variable is:

v
h h v v ( ) ( ) ( , ) =
where
v
h ( ) is the variogram on support v, ( ) h is the variogram on point
support and ( , ) v v is the average value of the variogram function inside a block v.
The impact on the variogram is shown in figure 7.4

Figure 7.4: Impact of regularisation on the variogram

C H 7 S U P P O R T
167

Note that another impact on the variogram is that the relative nugget effect
decreases as the size of support is increased.
Ret urning t o Our Example
The variograms of the 324 data have been computed along rows and columns and
plotted as figure 7.5. The variograms of the 2x2 and 3x3 blocks have also been
calculated and are shown on this figure.

Figure 7.5: Variogram & model for porostity data
We can see how the variograms have been modified as the size of support of the
ReV considered increases. Clearly, our aggregation exercise at the beginning of the
chapter is a series of regularisation steps.
Suppose that our information is the variogram of the original 324 measurements of
porosity, we will denote this
V1
.

We wish to use this variogram to deduce the variances of the other blocks:
V1 = elementary block
V2 = 2x2 block = 4V1
V3 = 3x3 block = 9V1
V6 = 6x6 block = 36V1
I mpac t on Co
Note that another impact on
the variogram is that the
relative nugget effect
decreases as the size of
support is increased.
C H 7 S U P P O R T
168

V = 18x18 block = 324V1 (whole deposit)
If we had a model for the point variogram ( ) h we could use the F function and
simply get:
D Vi V F V F Vi
2
( | ) ( ) ( ) =
In most practical situations, the supports on which our data are measured are
negligible with respect to the dimensions of the blocks we consider. As a
consequence, our data can generally be treated as point data
23
and their variogram
considered to be a point variogram.
In fact, in the case of this example, assuming that our original data are points is less
acceptable than it is in any mining situation, because V1 is only one fourth of V2.
For V3 the approximation becomes more acceptable.
The variogram of V1 shown in figure 7.5 was fitted as the sum of two spherical
models:
(h) = (h) + (h)
1 2

This model is shown in the figure. By application of the formula, using appropriate
values for the F-function, we obtained the results shown in Table 7.7. Note that
our variogram fit is not perfect (there is a slight hole effect not accounted for, for
example, and the model should probably have been fitted with a nugget effect).
However, our results for 3x3 and 6x6 blocks are very close to those observed from
the data themselves.
Note also, in Table 7.7, that the variance predicted by:
D v V
D o V
N
2
2
( | )
( | )
=
a relationship that presumes no spatial continuity, is shown.
Table 7.7 Variance for Different Supports
Support Observed Variance Variance Predicted by
Geostatistics
Variance Predicted by
D o V
N
2
( | )

3x3 Blocks 5.11 4.62 2.48
6x6 Blocks 1.99 1.76 0.62

23
It is possible to derive the point variogram from the sample variogram by mathematical
deconvolution, but this is rarely necessary in practice (and beyond the scope of this course in any case).
Poi nt Suppor t
In most practical situations,
the supports on which our
data are measured are
negligible with respect to the
dimensions of the blocks we
consider. Thus we can
consider samples as point
supports.
C H 7 S U P P O R T
169

These results clearly demonstrate that it is wrong to neglect spatial correlations
when predicting block variances. They also show that the variance is closely linked
to the support we consider. This is one of the main contributions of geostatistics to
mining problems
24
.

24
It should be noted that the model fitted (with no nugget effect) is optimistic. Even so, the results of
dispersion variance calculations accord well with the experimental estimation of variance. This suggests
that the geostatistical method is quite robust.
C H 8 E S T I M A T I O N E R R O R
170

8: Est imat ion Error
Truth lies within a little and certain compass, but error is
immense.
Herbert Hoover, Principles of mining valuation, organization and
administration. 1909
What is Ext ension Variance?
Geostatistics provides the practitioner with tools, via the variogram, that enable the
calculation of estimation variances.
Suppose that we want to assess the average value of the grade of a given domain V
using data from a smaller support v. For example the domain V might be a block,
and the support v might be a central core sample (see figure 8.1).

Figure 8.1 volumes (supports) discussed in the text.
Chapter
8
171

We wish to estimate the grade of Z(V) but we only have data for Z(v). It seems
natural to estimate Z(V) using the core sample grade Z(v). This is, of course the
polygonal estimation of the block by a central sample. We know that the grade of
the block will not always be equal to the grade of a central sample, so when
estimating the block grade in this manner this estimation, we will make an error.
What is this error?
First, under the assumption of the intrinsic hypothesis, Z(v) is an unbiased estimator
of Z(V), i.e.
E Z v Z V ( ) ( ) = 0
In general, the error is not zero. However, the average of all over- and
underestimations should be zero. Therefore, it is more interesting to characterise
the error made when estimating Z(V) by Z(v) using the variance, i.e.
E Z v Z V Z v Z V v V
e
( ) ( ) Var ( ) ( ) ( , ) = =
2
2

where
e
v V
2
( , ) is the extension variance. This is the variance of the error that we
incur in extending to the domain V the grade measured on domain v. In other
words, the extension variance
e
2
of the value of a sample taken in a block of ore is
the average squared error (or error variance) incurred in assuming that this sample
value is the true value of the block. In our example, the extension variance is thus
the average squared error made in assuming that the value of the sample extends
over the entire block
25
.
Ext ensi on Vari ance and Est i mat i on Vari ance
Conceptually,
e
v V
2
( , ) is simply the variance of the estimation of Z(V) by Z(v).
Often, the two terms estimation variance and extension variance are treated as
synonymous. The same notation (
e
2
) is also used, and conceptually the two are
equivalent. However, the term estimation variance is generally used with a broader
meaning: estimation variance is the sum of all error variances associated with
estimating the average grade of a given volume (block, bench, orebody). In
geostatistics, the term estimation variance is thus used for more general situations,
where several samples are combined to estimate a given area or volume.
The Formul a for Ext ensi on Vari ance
The theoretical value of the extension variance can be obtained by the formula:

e
v V v V V V v v
2
2 ( , ) ( , ) ( , ) ( , ) =

25
This is exactly the error made when using a traditional polygonal estimator for the panel.
Ex t ensi on
var i anc e
The value of a sample taken
in a block of ore is the
average squared error (or
error variance) incurred in
assuming that this sample
value is the true value of the
block.
172

where:
v is the small support (lets say, a sample or point) centrally located in V.
V is the larger support (block).
e
v V
2
( , ) is the extension variance just introduced.
( , ) v v is the mean value of the variogram between two points sweeping
independently within the volume v. This is the dispersion variance of
points within a support of size v. This is easily obtained by the auxiliary
function F(v) introduced in the previous chapter.
( , ) V V is the mean value of the variogram between two points sweeping
independently within the volume V. This is the dispersion variance of
points within a support of size V. This is easily obtained by the auxiliary
function F(V) introduced in the previous chapter.
( , ) v V is the mean value of the variogram between two points, one
sweeping independently within v and the other sweeping independently
within V. This is the dispersion variance of support v within a support of
size V. This value can also be obtained via an auxiliary function.
These concepts are illustrated in figure 8.2.

Figure 8.2 Concepts of extension variances

173

Formula (i) applies for any shapes for v and V; in particular v need not be included
in V. The factors influencing the variance of extension are:
(i) The regularity of the variable through the model of ( ) h
(ii) The geometry of V through ( , ) V V
(iii) The geometry of v through ( , ) v v
(iv) The location of v with respect to V through ( , ) v V
Fact ors Affect i ng t he Ext ensi on Vari ance
If we consider formula (i) again:

e
v V v V V V v v
2
2 ( , ) ( , ) ( , ) ( , ) =
we can re-write it, by rearranging into two terms, as:
{ } { } ) , ( ) , ( ) , ( ) , ( ) , (
2
v v V v V V V v V v
e
+ =

This makes it clear that the extension variance
e
v V
2
( , ) decreases as:
The sampling v of the domain to be estimated V becomes larger. We
can see this by considering the extreme case where v=V. In such a
case, ( , ) V V is identical to ( , ) v v . In this case the two terms is (ii)
above are equal and
e
v V
2
( , ) is zero.
The variogram is more regular, i.e. the ReV is more continuous.
174

With regard to the second factor, a highly discontinuous variable would have a
variogram approaching that of a pure nugget effect. In this case, a sample within
the block is not representative of the block grade at all and no local estimation is
possible. By estimating any block, we make a maximum average error in this case.
This is an interesting result, because one sometimes hears someone exclaim we use
a polygonal estimator
26
for grade control blocks because the variogram is poorly
defined (i.e. pure nugget). In fact, this is the most disastrous circumstance in which
to use this type of estimator!
Note also that, if only one sample is available for a given block it seems logical to
assume that a central location for this sample is optimal, in the sense of minimising
e
2
. This is borne out by geostatistical theory: the extension variance attached to
assigning the grade of a sample at one corner to a block, for example, is higher than
that resulting from using a central sample
27
.
Ot her Propert i es of Ext ensi on vari ance
An obvious, but important property of extension variances is that they involve only
the geometry of the samples/blocks and the variogram model: they do not involve the
actual samples involved in a particular situation. This means that determining the
appropriate sampling geometry by comparing estimation variances different
situations requires only an acceptable variogram model.
On the other hand, it does not take into account local conditions, for example, if
we wish to estimate our block by a central sample that happens to be the maximum
grade for the deposit, we expect a worse error variance than the average error
variance provided by the extension variance.
Ext ension Variance & Dispersion Variance
The extension variance
e
v V
2
( , ) should not be confused with the dispersion
variance D v V
2
( | ), although we use dispersion variances in determining the
extension variance.

26
Or inverse distance squared which is very polygonal in nature (i.e. similar to nearest neighbour).
27
If we have a "pure nugget effect" model for the variogram, the two extension variances are equal: this
is the limiting case.
175

In summary:
Table 6.1 Extension Vs Dispersion Variance
Dispersion Variance D v V
2
( | ) Extension Variance
e
v V
2
( , )
This is the variance of grades defined on one support
v within another support V
e.g. the variance of points within a block
or
the variance of cores within the deposit
Physical Significance
This is the variance of the error we make when
assuming that the grade of one volume v is the true
grade of a larger volume V
e.g. if we estimate a 5m x 5m x 5m block by a
central, 5m high drill hole sample
or
we estimate the average thickness of a coal seam in a
100m x 100m area by a single measurement located
at one corner
Useful Concept

To make it quite clear: the dispersion variance D v V
2
( | ) has a physical significance: it
measures the variance of samples of size v within the domain V. In contrast, the
extension variance is a useful concept that allows us to characterise the error
associated with estimating a volume by a sample of given support.
Again, in many cases, the volume of our samples is very small in comparison to the
blocks we consider. Consequently, we can consider the sample support to be point
support. Our formula is then simplified to:

e
o V o V V V
2
2 ( , ) ( , ) ( , ) =
Di sper si on vs
Ex t ensi on
Dispersion variance deals
with support, while
extension variance deals
with estimation errors.
176

Pract i cali t i es
Auxiliary functions are available to calculate all the terms required to evaluate
various extension variances. The F-Function and other auxiliary functions do not
have convenient analytical forms, so they have historically been obtained via charts
or tabulations of the values (see Journel and Huijbregts, 1978), but are now
obtained through computer programs. These programs can give the necessary
values to allow calculation of extension variances for a variety of situations (1D,
2D, 3D, point within block, point at margin of block, etc.)
Note that the resultant extension variance
e
2
applies to a single block V.
Combi nat i on of El ement ary Ext ensi on Vari ances
In order to calculate the combined estimation variance
E
2
when estimating a
volume V composed of N elementary blocks, each of volume v and possessing
associated elementary extension variance
e
2
a method known as combination of
elementary extension variances (Journel and Huijbregts, 1978, p.413) can be employed.
The formula used is simple:

E
e
N
2
2
=
The resultant estimation variance
E
2
is that associated with estimating the mean
grade of a volume V from N samples, each centrally located in one of N unit
blocks v with elementary extension variance
e
2
. It does not account for any error
associated with estimation of the geometry of the mineralisation.
AN I MP ORT ANT AS S UMP T I ON
The method of combination of elementary extension variances also assumes that
the error made for any block is independent of the errors made for other blocks; this is
generally a valid assumption if blocks are fairly large and there is only one sample
per block.
177

Geomet ry of Mi neral i sat i on
When estimating a zone from a number of samples, the error associated with
estimating the geometry of this mineralisation must also accounted for.
Given that there are n regularly spaced drill holes in mineralisation (however this is
defined), the following formula gives a good estimate of the relative variance of
estimation for a surface (David, 1977):
s
s n
N N
N
N N
2
2 2
2 1
2
2
2 1
1
6
0061 = + ( . )

Derivation of this formula (due to George Matheron) was by means of calculating
estimation variances of an indicator variable where each drill hole has a value 0 for
waste and 1 for ore. There are n positive, i.e. above cut off, regularly spaced drill
holes, each central to a block (v ) of dimensions l x L; there are thus n blocks.
There are N
1
blocks in one direction and N
2
in the other ( ) N N
2 1
.
Having calculated an extension term
E
2
and a surface term
s
2
a total error term
T
2
can be calculated
28
:

T E S
m m s
2
2
2
2
2
2
= +
The geometric error
s
2
in this case would be assessed using a two dimensional
methodology. A three dimensional problem would therefore be reduced to two
dimensions and the results would be indicative only.

28
An example of additive error terms is given by David (1977, example 8.6.1, pp.221-225). Various
formulae and examples are also given by Journel and Huijbregts (1978, section V.C. pp.410-443).

Not e
This approximation is two
dimensional.
178

Sampling Pat t erns
The idea of extension variance and combining elementary extension variances
allows us to compare the efficiencies of sampling patterns (or sampling geometries).
The are three broad types of sampling geometry as illustrated in figure 8.3.

Figure 8.3 Sampling patterns and clustering (sampling geometries)
Considering each of these separately:
Random Pat t ern
Random sampling would be unusual in mining practice, however there are
instances where old data, or intersections in a vein at depth (due to lack of control
on deep holes) might follow this pattern.
In order to estimate the average value Z V ( ) over V we take the average of N
samples Z x ( )
i
randomly scattered within V. We will assume that our samples
Z x ( )
i
have point support (i.e. that they are very small in relation to the domain
being estimated). It can be shown that the variance of the error is:
E
N
D o V
2 2
1
= ( | )
179

where D o V
2
( | ) is simply the dispersion variance of points in the domain we are
estimating, i.e. the variance of the samples.
Random St rat ifi ed Gri d (RSG)
This time, V is divided into N similar sub zones. Within each sub zone, a sample is
taken at a random location. Hence this pattern is less random than a truly random
sampling. Intersections in a vein at depth that are intended to be on a regular grid
in the plane of the vein might follow this pattern simply as a consequence of hole
deviations. RSG's are also sometimes used in geochemical soil surveys.
In this case it can be shown that the variance of estimation has the same form as for
the purely random case, and is:
E
N
D o v
2 2
1
= ( | )
Note that D o V
2
( | ) is replaced here by D o v
2
( | ). Since we know from the Krige's
relationship that D o V
2
( | )is always greater than D o v
2
( | ):
D oV D o v D v V
2 2 2
0 ( | ) ( | ) ( | ) =
So, the estimation variance for an RSG will always be lower than for a purely
random grid, since:
E
N
D o v
N
D o V
2 2 2
1 1
= < ( | ) ( | )
This shows that the Random Stratified Grid is always more efficient than a purely
random pattern.
Regul ar Gri d
We have seen that in this case the estimation variance can be approximated by the
principle of combination of elementary extension variances, i.e. it can be approximated by
dividing the extension variance of a central sample in a unit block by N (the
number of informed elementary blocks):

E
e
N
2
2
=
We can calculate (using auxiliary functions) the estimation variance of a given grid,
for a specified domain V and known variogram model. Delfiner (1979) gives an
comparison for a linear variogram model, showing that for a given situation, the
ratio between the estimation variance for an RSG and a regular grid is about 2.14.
In other words, a regular grid is better than twice as efficient as an RSG (for the
same number of samples).
We know that the RSG is always more efficient than a totally random pattern. In
fact, Delfiner gives a comparison for the three cases when the domain V is a
square.
180

He expresses the estimation variances in terms of the sample variance
( [ | ])
2 2
= D o V and the number of samples N:
Table 6.2 Estimation variances for the average grade over
a square (with a linear variogram and N samples))
Random Pattern RSG Regular Pattern
2
N

2
3 2
N
/

2
3 2
214 .
/
N

We can appreciate the benefit of a regular sampling pattern from this table. The
variance is reduced considerably as our sampling geometry becomes more regular.
A regular sampling pattern exploits the spatial correlation of the grades: putting two
samples very close together is producing redundant information, and (given a
limited number of samples) implies that some other part of the domain must be
under-sampled.
Similar results can be determined for a bounded variogram model (say, spherical),
but the estimation variance now depends upon the range a of the variogram.
It can be demonstrated that the regular grid will still perform better than the RSG,
but the advantage becomes reduced as the size of the grid square becomes large
relative to the range of the variogram.
Again, this accords with common sense: as the unit cell in our grid becomes much
larger than the range of the variogram, the influence of a sample becomes,
relatively, quite localised. Consequently, the strategic superiority of the central
location declines. In fact, as a becomes small relative to the dimensions of our grid
cell, the situation more closely approaches that of a pure nugget effect model (i.e.
a 0).
Delfiner gives the following example, in which he tabulated, for various cell sizes,
the dispersion variance of points in a cell v (the estimation variance of an RSG is
proportional to this) and the extension variance of the same unit cell (using a
spherical model) as seen in the following table.
181

Table 6.3
Dimension of
Grid in Units
of Range (a)
D o v
2
( | )
e
o v
2
( , )
ratio
0.15a 0.118 0.056 2.107
0.2a 0.115 0.074 2.094
0.4a 0.31 0.15 2.067
0.6a 0.45 0.235 1.915
0.8a 0.56 0.32 1.75
1.0a 0.66 0.41 1.61
1.5a 0.81 0.65 1.25
2.0a 0.88 0.80 1.1
3.0a 0.94 0.92 1.02
5.0a 0.977 0.96 1.017
8.0a 0.9906 0.99 1.00
Note that, after the length of the side of a cell exceeds the range of the variogram,
the advantage of the regular grid falls away rapidly. Another way of looking at this
is that the estimation variance associated with a single cell climbs very quickly if the
grid spacing is too wide.
C H 1 1 S I M U L A T I O N
182

9: Kriging
While the inverse of the distance squared may have some physical relation
to the gravitational attraction of masses, it has nothing whatsoever to do with
the distribution of grades in a mineral deposit.
A.G. Royle M.Sc. Mining Geostatistics Lecture,
University of Leeds, 1990
The Problem of Resource Est imat ion
Sampling data from drill holes, channels etc. provide the geologist and mining
engineer with fragmentary information. The problem we face when performing
resource estimation is to obtain an idea of the grade of the whole deposit, or of
specific blocks of ground within the deposit. The only solution to this problem is
to make estimates.
No data processing, mathematics or computer program can ever tell us what the
grade of an un-sampled point in our deposit is. There is always uncertainty:
1. Between sampled locations (refected by the spatial component of the
variogram, and
2. At the samples themselves (this is reflected in the nugget effect, as we have
discussed earlier).
The variogram is thus a model for spatial uncertainty, and a vital input to designing
sensible estimation approaches.
So we must make estimates, and the aim is surely to make the best estimates we
can, to use our data efficiently, i.e. to get the most out of our information (the
samples). We will look at the issue of best shortly; first, lets consider the idea of
estimation by interpolation in a bit more detail.
Most geologists are comfortable with the idea of using some sort of weighted
average of sample values to estimate blocks in a mineral deposit. A classical
method for doing this is the use of inverse distance weighting (IDW).
Chapter
9
Unc er t ai nt y
No data processing,
mathematics or computer
program can ever tell us
what the grade of an un-
sampled point in our deposit
is. There is always
uncertainty between sampled
locations.
C H 1 0 N O N - L I N E A R E S T I M A T I O N

183

In IDW methods, the weighting coefficients (or more simply the weights) applied
to a sample are a function of the position of the sample relative to the block being
estimated. Samples close to the block get higher weights than those far away. Some
general idea of the variability of the mineralisation may be introduced (by using
higher powers, for instance, weighting by the inverse of the distance squared, or
cubed etc.), but no real reference is made to the variability of the particular orebody
under consideration.
That IDW should be more appealing to mining geologists than polygonal methods
is not surprisinggrades in mineral deposits are, almost invariably, correlated in
space, often up to quite large distances. Because of this correlation, samples
external to the block being estimated can reveal information about the block grade,
and thus improve estimation accuracy compared to polygonal methods. Methods
that use weighted averages of local data thus represent a significant improvement
over polygonal methods.
However, there is no reason that IDW weighting should be applicable to ore
deposits, or, putting it another wayto quote A.G. Roylewhile the inverse of
the distance squared may have some physical relation to the speed of light in a
vacuum, it has nothing whatsoever to do with the distribution of grades in a
mineral deposit. It has never been made clear by any of its proponents why any
particular power of the inverse distance should be used in resource estimation
practice.
What Do We Want From An Est i mat or?
What do we desire of an estimator? At the very least we require an accurate estimate,
i.e. we wish our estimates to be (on average) as close to the true grades as possible.
The accuracy of estimates depend on a number of factors, i.e. those that affect the
estimation variance
e
2
introduced in the previous chapter:
1. The number of samples and the quality of the data for each sample.
The quality may vary quite significantly from one sample to another. Our
estimator should not necessarily grant the same importance to each sample
used for the estimate.
2. The geometry of samples in the deposit. In particular, clustering of
samples may make some sampling information redundant, at least in part.
In general, an even distribution of samples in the deposit achieves better
coverage and gives more information than an equivalent number of
samples that are locally clustered.
3. The distance between a sample and the area we wish to estimate. If
we wish to estimate a particular block, it is natural to place more weight on
samples close to the block of interest than on more distant samples.
Similarly, if we wish to make point estimates (for example, of a thickness
variable) we expect our estimator to be exact at the point where we have
data, more reliable close to sample points, and to deteriorate as distance to
the nearest sample increases.
I nt er pol at i on
Methods that use weighted
averages of local data thus
represent a significant
improvement over polygonal
methods.

184

4. The spatial continuity of the interpolated variables. We should require
more than an arbitrary falling away of weight as distance to the block or
point being estimated increases, such as provided by IDW. We should also
require that the spatial variability of the variables is incorporated into our
estimates. Variables with very smooth variations (for example the top of a
gently deformed geological horizon) should not be weighted in the same
manner as variables with more erratic spatial fluctuation, like metal grades.
We desire that our estimator is unbiased, i.e. the average estimation error should be
zero (so that the average of the estimates should always equal the average of the
true grades).
We would also like to have an index of the reliability of the estimates.
Why Kriging?
Kriging is an estimation method that takes into account the factors we have just
presented as being desirable for an estimator. These properties derive in part from
the fact that kriging utilises the modelled spatial correlation (estimated from the
sample data) to assign weights.
The term kriging was coined by G. Matheron of the Centre de Geostatistique at
Fontainebleau in honour of D.G. Krige, who pioneered the use of statistical
methods in resource estimation in South Africa in the 1950's. Kriging has been in
widespread use since the early 1970's, initially in the Western European and South
African mining industries.
Today kriging is used by many mining companies in North and South America,
Australia, Africa, and Asia. Its use has also spread to many non-mining problems
(petroleum, environment, hydrology etc.).
BLUEBest Li near Unbiased Est i mat or
The desirable properties of kriging are often summarised by the acronym BLUE
Best Linear Unbiased Estimator:
Best
Kriging is best in the sense that it is has minimum mean squared error, i.e. the
expected squared difference between the estimate Z
0
*
and the true value Z
0
:
E Z Z [ ]
*
0 0
2

is a minimum for all possible linear estimators.
Linear
Spat i al
Cor r el at i on
Variables with very smooth
variations should not be
weighted in the same
manner as variables with
more erratic spatial
fluctuation, like metal grades

185

Linear estimators are those formed by a linear weighting of the available samples,
i.e.
( )
i
N
i
i
x Z Z =
=1
*
0

Where the
i
are the weights, and the estimate Z
0
*
is a weighted sum of the data
values ( )
i
x Z at each point x
i
. Note that IDW methods are also linear, as are
polygonal methods. In polygonal methods, there is a single weight (1.0) applied
only to the sample falling inside the block or polygon. Note also that, as stated
above, by the criteria of minimum estimation variance, kriging is best of all
possible linear estimators by design (given a specific estimation geometry and
variogram model).
Unbiased
The unbiased condition is important. It specifies that the expected error:
E Z Z [ ]
*
0 0

is equal to 0 (zero). We will discuss this property in more detail later.
Estimator
Kriging is an estimator. Because we cannot know the true grade at an unknown
point, we must employ some method to estimate it.
So, kriging is the best linear unbiased estimator of the quantity to be estimated. It
achieves this by giving the samples informing the estimate weights designed to obtain
an estimate with the minimum mean square error. We will see that the properties
of kriging make it superior to the IDW, polygonal (or any other linear) method.
How Kriging Works
The derivation of kriging equations is often a stumbling block for geologists and
engineers wishing to use these methods. They may appreciate the theoretical and
practical advantages of kriging, but have difficulty understanding exactly what is
going on to calculate the weights used in a computer kriging program.
If you get a feel for what the terms in the kriging equations mean, how the
variogram model affects the weights etc., you will be more confident in setting up
and running your own kriging.
Our aim here is to introduce and explain the kriging equations with a minimum of
mathematics. The references at the end of this manual, in particular Journel and

186

Huijbrechts (1978), provide exhaustive derivations of kriging with all the attendant
mathematical rigour.
Our eventual goal here is to be able to look at kriging equations and understand
each term.
Kri gi ng Made Si mpl e?

Ordinary Kriging (OK) is a geostatistical method of local estimation by
interpolation. It is a linear method, i.e. based on a linear weighted average.
The basic principles of OK are:
A search is made around the block to be estimated. Samples located within
the search neighbourhood are utilised for estimation of the block in
question, whereas samples outside this neighbourhood are not used.
The samples within the search are assigned weights that reflect the spatial
variability of grade (as characterised by the relevant variogram model).
A weighted average is calculated to produce the block estimate.
The advantages of OK over other, non-geostatistical interpolations (for example
inverse distance weighting) are:
OK weights are based on the data themselves (via the variogram model)
rather than being arbitrary (as is the case for inverse distance).
Because of this, OK estimates correctly account for nugget variance and
short-range structures.
OK weights reflect better the anisotropy of spatial grade distribution,
compared to non-geostatistical interpolators.
OK estimates reflect the support of the estimated block and the informing
data.
A major, well-known advantage of OK is that the optimal interpolation
weights assigned to data are calculated in such a way that they minimise the
variance of the estimation error.
The problem we have is to obtain an estimate at an un-sampled location (a block is
just an un-sampled location with non-point volume). We will obtain this estimate
using a linear weighted average:
( )
i
N
i
i
x Z Z =
=1
*
0

Advant ages of OK
Ordinary kriging weights are
derived from the sampling
data

187

Our problem is to choose the weights
i
in the best possible way to achieve the
desirable properties we presented at the beginning of this chapter.
At its simplest, kriging is just a weighted average, where the weights are chosen in
this best possible way.
As for IDW, in a kriging we allocate weights to the samples found within a defined
search neighbourhood in order to obtain a linear estimate. These are the kriging
weights.
What makes kriging different to other linear weighted averages is that it is firmly
based upon the probabilistic model we have introduced in the earlier chapters of
this course.
In particular, kriging employs the variogram model as the weighting function. Because
of this, kriging weights are assigned in a way that reflects the spatial correlation of
the grades themselves. This represents a real step forward from using arbitrary
weighting functions that bear little relation to the nature of grade distribution (like
IDW).
The Advant ages of a Probabi li st i c Framework
Using the framework of random functions and specifying a variogram model
allows us to calculate the variance of the average error we will make by estimating the
grade of a block using data with a given spatial (or geometric) configuration.
It is being able to calculate the average error that gives us the opportunity to minimise
it. Only a probabilistic approach allows this.
In summary, kriging is a linear weighted average that uses the variogram as a
weighting function. Kriging formulates the weights in the framework of random
function models and it is this that allows us to obtain minimum variance
estimations.
Advant ages of OK
Ordinary kriging weights
result in minimum
estimation variance for any
linear interpolator.

188

Kriging Equat ions
Consider the situation where we wish to estimate the grade of a block using the
surrounding data (a situation illustrated by figure 9.1).

Figure 9.1 Estimating a block by a number of data

Our estimate will be a linear weighted average, or linear combination, of the available
data:
( )
i i
N
i
x z z =
=1
*
0

Note that here the values z(x) are values of data (indicated by using lower case).
This expression just says: the estimate z
0
*
is equal to the sum of each data value
( )
i
x z multiplied by a weight
i
. So, for each of the samples we use to form the
estimate, we assign a weight. There are N samples, and therefore N weights:

i N
=
1 2 3
, , ,...,
We are going to view this problem in terms of a probabilistic or statistical model. So
we will represent both the estimate and the data as random functions:
( )
i i
N
i
x Z Z =
=1
*
0

Choosi ng t he Best Wei ght s
We now wish to determine the weights
i
so that Z
0
*
is:
1. Unbiased: E Z Z [ ]
*
0 0
0 =
2. Result is an estimate with minimum mean squared error, i.e. E Z Z [ ]
*
0 0
2

is minimum.
When condition 1 is satisfied, the mean squared error is also the variance, i.e. it is
the squared deviation about the mean. So, from here on we will refer to the error
variance or kriging variance rather than the mean squared error.

189

The Unbi ased Condi t i on
The unbiased condition entails that:
( ) 0
0 ] [
0
1
0
*
0
=
=
Z x Z E
Z Z E
N
i
i i

If Z(x) is stationary, the expectation of Z(x) is equal to the mean:
( ) m x Z E
i
= ] [
and also the expectation of the true grade Z
0
is equal to the mean:
E Z m [ ]
0
=
So, if Z(x) is stationary the expected values of both the true value and any given
sample value are both equal to the mean, we can write the unbiased condition as:
( )
( ) [ ]
0
0
0
1
0
1
0
1
=
=
=
=
=
m m
Z E x Z E
Z x Z E
N
i
i
i
N
i
i
i
N
i
i

We can factorise this last expression by taking the value m as a common factor:
0 1
0
1
1
=
=
=
N
i
i
N
i
i
m
m m

Dividing both sides by m...
1
0 1
0 1
1
1
1
=
=
=
=
=
=
N
i
i
N
i
i
N
i
i
m

Unbi ased
Ordinary kriging weights
result in globally unbiased
estimates (as do IDW
weights). However, OK also
minimises conditional bias
because it minimises
estimation variance.

190

So, t he unbi ased condi t i on i s sat i sfi ed i f we ensure t hat t he sum of t he
wei ght s i s equal t o 1.
This is an intuitive outcome, and most estimation methods in fact satisfy this
condition. For example, like any linear combination, the IDW estimator can be
written:
( )
i i
N
i
x z z =
=1
*
0

where the
i
are determined as follows:
i k
d
=
1

Where d is the distance between the point to be estimated z
0
and the given datum
( )
i
x z . This distance is raised to some power k. In practice, these weights are set to
equal unity (1.0).
Mi ni mi si ng The Error Vari ance
The error variance is simply the variance of the errors:
Z Z
0 0
*

The error variance for the stationary case is the expected value of the squared error:
E Z Z Var Z Z [ ] [ ]
* *
0 0
2
0 0
=
This variance is the kriging variance if the estimate Z
0
*
is obtained by kriging. We will
now see how we can minimise this variance.
Terms i n t he Kri gi ng Equat i ons
29

The error variance can be mathematically expressed in terms of the variogram
function. We will step through all the terms in the following equation to make
them clear (see also figure 9.2):
) , ( ) , ( ) , ( 2
] [ ] [
0
*
0
2
0
*
0
V V x x V x
Z Z Var Z Z E
j i j i i i
=
=

where:

29
Note that most presentations of the kriging equations in the geostatistical literature are expressed in
terms of covariances not variogram values. In this presentation, we use variogram values, because
presentation of these ideas to geologists over many years has indicated to the authors that this is more
intuitiuve.

191

( , ) x V
i
is the average value of the variogram calculated between x
i
and
the volume V, i.e.
dx x x
V
V x
V
i i
) (
1
) , ( =

( , ) x x
i j
is the value of the variogram between the points x
i
and x
j
, i.e.
between samples.
( , ) V V is the average value of the variogram between any two points x
and x sweeping independently throughout the volume V, i.e.
) ( ) (
1
) , (
2
V F x dxd x x
V
V V = =

This is the dispersion variance of points in a block V.

Figure 9.2 Extension and dispersion variances in the kriging equations
Recall that our aim is to minimise the variance of estimation. In order to minimise
the variance under the constraint that the sum of weights equal 1.0. In order to do
this we must solve a system of n+1 equations that contain only n unknowns. There
are n equations each containing one of the n weights
1 2 3
, , ,...,
n
; the
additional equation being the unbiasedness condition: the sum of these weights
equals one.
The Lagrange Paramet er
The technique of Lagrange parameters (or Lagrange multipliers) is suited to the solution
of this type of problem
30
. The technique of Lagrange parameters is a mathematical
procedure for converting a constrained minimisation problem to an unconstrained
one. In essence, another unknown (the Lagrange parameter) is introduced into
our equation.
If you recall minimisation from calculus, you will remember thatif we wish to
minimise some function with respect to the
i
'swe need to set the partial
derivatives with respect to the
i
's to zero. In fact, we introduce the Lagrange
parameter as follows:

30
We introduce the Lagrange technique here with no detailed description or derivation (these are beyond
the scope of this course). However, the interested reader is referred to any of the usual university calculus
texts, for example, Leithold (1986) for a full description of this method.
Lagr ange
In essence this parameter is
a dummy variable used to
solve a particular class of
minimisation problem.

192

=
=
1 2 ) Var(
1 2
1
0
*
0
1
2
N
i
i
N
i
i e
z z

(i)
Note that the function is simply the estimation variance with the addition of the
term:

=
1 2
1
N
i
i
(ii)
Since we have set the term:
i
i
N
=
=
1
1 0
(because the sum of the weights equals 1), the additive term (ii) equals zero. So, by
adding this term, we are not altering our equation, simply re-writing it to make
minimisation convenient. We set the partial derivatives of equation (i):
i i
and
to zero in order to obtain the set of 's that satisfies our minimum variance criteria.
We obtain the following system of linear equations, known as the ordinary kriging
system:

i
j
N
i j i
i
j
N
x x x V i N
=
=
+ = =
=
1
1
12
1
( ) ( , ) , ,...,

The minimum of the variance (called the kriging variance is then given by:
+ = =

=
) , ( ) , ( ) Var(
1
0
*
0
2
V V V x z z
i
N
i
i OK

Note that, when the variogram model is a pure nugget effect Co we obtain:
i
N
=
1


193

i.e. each sample gets an equal weight, regardless of its spatial location with respect
to the block we are estimating. This makes sense, because a pure nugget model
indicates that no spatial correlation exists, consequently, samples close to the block
(or within it) tell us no more about the block grade than distant samples.
In the case where V is a point, the point block variance reduces to the point-point
variance:
( , ) ( ) x V x x
i i
=
0

and
( , ) ( ) V V = = 0 0
The kriging system is often presented in a matrix form (since this is how computer
programs solve the equations
31
):
=
1
) , (
) , (
) , (
0 1 1 1
1
1
1
B X A
2
1
2
1
2 1
2 22 21
1 12 11
V x
V x
V x
NN
N
N N N
N
N

M
M
L
M O
L

In the above equation:
A is a matrix of the variogram values between samples (expressed in
terms of the variogram).
X is a matrix containing the weights we wish to obtain.
B is a matrix containing the sample-block variogram values (again,
expressed in terms of the variogram).
If is an admissible variogram function, then the solution is straightforward:
AX =B
X =A B
-1

Where A
-1
is the inverse of A.

31
Computers calculate the terms in covariances rather than variogram values, however.
Pur e Nugget
In OK, with a pure nugget
model, all weights are equal,
regardless of how far we
searchin other words,
local estimation is not valid!
Li near Al gebr a
For details of the solution of
simultaneous equations by
matrix methods, refer to
texts on linear algebra in the
references to this manual.

194

Propert ies of Kriging
We started this chapter by examining the desirable properties of an estimator. We
note that kriging takes into account the following elements:
1. The relative positions of the estimated block V and sample locations x
i
,
through the terms ) ( or ) , (
0
x x V x
i i
in the case of estimation of a
point.
2. The distances between samples, through the terms ( ) x x
i j
.
3. The structure of the spatial variability peculiar to the mineralisation under
consideration, i.e. ( ) h . The kriging weights
i
are tailored to this modelled
spatial continuity.
Exact Int erpol at i on
Unlike some estimators, for example trend surfaces, or simple linear regression,
kriging is an exact interpolator. This means that when we estimate point values,
kriging restores at the data points, the measured value. This is a property of the
kriging, not an ad hoc adjustment.
This property can be easily checked in the kriging system. If x x
i 0
= then the
solution is:
i
j
j i
=
=
1
0 and for

In fact, this corresponds with our intuitive notion of how a good estimator should
behave. We can go back to first principles, and consider the squared error that we
are attempting to minimise:
E Z x Z x [ ( ) ( )]
*
0 0
2

This error is obviously minimised when the point estimate at a sampled location is
identical to the (known) sample value:
Z x Z x
*
( ) ( )
0 0
=
and this minimum is clearly equal to 0. This is one attribute of kriging that makes it
especially suited for contouring applications, because the data points are honoured
exactly.
Note: This property is a property of point kriging. Point kriging simply replaces the
point-block variogram values in matrix B, above, with a vector of (sample)point-
(unknown)point variogram values. We do not expect block kriging estimates to
honour the data because we know (from the information effect) that some degree
of smoothing is required to minimise conditional bias.
Ex ac t i t ude
We do not expect block
kriging estimates to honour
the data because we know
(from the information
effect) that some degree of
smoothing is required to
minimise conditional bias.

195

Uni que Sol ut i on
The kriging system always has a unique solution, providing that the variogram model
used is positive definite. This is another reason why only admissible functions can
be used for variogram models.
Kri gi ng Syst ems Do Not Depend On t he Dat a Val ues
The kriging weights depend upon the data in the sense that the variogram model
we choose is intimately linked to the histogram and spatial continuity of the
samples themselves; however, the kriging equations contain no reference to the
data values themselves. This means that the set of weights we will obtain for a
given sampling geometry and a specified variogram model are the same, regardless
of the particular grades of the samples
32
.
For example, if we consider a zone with one defined variogram model and a
regular rectangular sampling grid, there will be one set of kriging weights to derive
(since each block will be informed by identically located samples, in a relative
sense). Historically, this property could be used to vastly increase the efficiency and
speed of grade control kriging. These advantages are not so striking with modern
computers!
Because of this property, it is important that we take care to define the variogram
properly and we must have enough data to be confident of the ( ) h model we
select.
Combi ni ng Kri gi ng Est imat es
Theoretically, if we discretise a block V into a very large number of points (say 100
or more) and perform a point kriging for each, the average of these point estimates
equates to the block estimate. However, this process is very inefficient and is never
used in practice. Using the point-block covariances (via the variogram model)
allows us to much more efficiently obtain block kriged estimates.
Infl uence of t he Nugget Effect on Kri gi ng Wei ght s
In the chapter on variography, we emphasised that the short scale behaviour of the
variogram was critical in kriging. In particular, the nugget effect has a strong
influence on the kriging weights:
Screen Ef fect
If we have a small nugget effect, i.e. very continuous ( ) h , then the weighting will
be heavily biased towards the block being estimated and its immediate neighbours.
This is called the screen effect, because the nearby samples are considered to screen
the outer samples from receiving significant weights when there is a small nugget
effect. Again, this makes sense intuitively, because we would desire our estimator to
give the closest samples the majority of weight in the case of pronounced spatial
continuity. A strong screen effect means that the kriging is not very smoothed.

32
This is true for IDW also. The difference is that the weights in IDW are arbritrary, whereas those for
OK are derived from data correlations.
Di sc r et i si ng
In IDW, discretisation
involves estimation of an
array of point values and
recombination. In kriging
the discretisation is used to
calculate point-block
variogram values. Block
kriging estimates blocks!

196

The Case of Low Nugget Effect , Hi gh Cont i nui t y
If we have a more continuous model for ( ) h , for example in for a topographic
variable, the closest samples provide all the information required to obtain a good
estimate.
In the extreme case of absolute (table-top) continuity, the closest sample is
sufficient, and polygons/nearest neighbour methods work well! In this case there is
a very strong screen effect and the smoothing is complete.
The Case of Hi gh Nugget Effect , Low Cont i nui t y
If we have a more discontinuous model for ( ) h , for example in some precious
metal deposits, more and more distal samples will receive non-zero weights. In the
extreme case of pure nugget effect, all samples receive equal weight.
In fact, the case of pure nugget effect implies that no local estimation can be made:
the best estimate of a block V is the mean grade of the deposit. In this case there is
a total absence of screen effect and the smoothing is complete.
Simple Kriging
The kriging introduced on the preceding pages is ordinary kriging (OK). This is the
kriging implemented in most mining packages. The system can be adapted for
strictly stationary conditions to yield the simple kriging (SK) system. Since strict
stationarity implies that the following condition is respected:
Z x m ( ) = 0
where m is the mean, we do not have to set:
i
i
N
=
=
1
1
as a condition. SK is very useful when determining the kriging neighbourhood (i.e. the
area or volume with which we will limit our search for samples). In SK we
determine a weight to be assigned to the mean
m
such that:

m i
=
1
The larger
m
is, the weaker we expect the screen effect to be. Consequently, we
choose a larger kriging neighbourhood as
m
increases, all things being equal
(Rivoirard, 1987c).
Kriging Pract ice
The steps in kriging are straightforward:
Smoot hi ng
The simple rule is: as the
continuity decreases, we
must search further to
minimise conditional bias.
SK vs OK
SK has no real applications
in mining, for linear
estimation. It forms the
basis of some non-linear
approaches however. For
linear estimation of grade,
SK is not recommended,
because the stationarity
assumptions are too strong.

197

1. Preliminary data analysis and cleaning.
2. Definition of zones of interest (each treated separately in the steps below).
3. Any data transformation (e.g. logarithms).
4. Structural analysis to obtain a variogram model.
5. Specification of grid spacing/block dimensions, boundaries.
6. Specification of kriging neighbourhood or quantified kriging
neighbourhood analysis: take into account the range, but do some trial and
error calculation of weights to establish efficient neighbourhood
dimensions. Note that the neighbourhood can be smaller than the range
where there is a strong screen effect (low relative nugget variance), and may
need to be larger than the range if there is only subtle screen effect (high
relative nugget variance).
7. Perform the kriging.
8. Interpret the results.
Steps 1 and 8 are often rushed (or left out), and in our experience it is common
for steps 2, and 5 to be performed with insufficient thought. Step 6 is rarely
employed, and in effect makes the difference between good and poor quality of
kriging. We therefore discuss this important step in detail, below.
Kriging Neighbourhood Analysis
Refer also to Rivoirard (1987).
The criteria to look at when evaluating a kriging configuration are the following:
1. The kriging variance.
This is an indicator of the quality of the estimation, and depends on the number of
data used in the estimation and on the variogram.
Note: We recommend that the kriging variance not be used for building
confidence intervals because this step requires supplementary hypotheses
(Gaussian distribution of errors) which are rarely, if ever, met in mining situations.
2. The slope of the regression true block grade vs the estimated block grade.
The slope of this regression can be calculated once the variogram model a, block
size, sample locations etc. are specified. The slope is given by the expression:
) (
) , (
*
*
v
v v
Z Var
Z Z cov
a = ,
KNA
Quantified kriging
neighbourhood analysis or
KNA, forms the basis of
scientific application of
kriging.
Kr i gi ng Var i anc e
This gives an idea of relative
quality of estimation, but
maps of regression slope are
equally useful.

198

where p is the slope of the regression, Z
v
is the true block grade and Z
v
*
is the
estimated block grade.
Ideally a should be very close to one. This implies conditional unbiasedness. In
these circumstances, the true grade of a set of blocks should be approximately
equal to the grade predicted by applying a cut-off to the OK estimation.
3. The weight of the mean in a simple kriging.
Instead of performing an ordinary kriging (OK), where the sum of the weight is set
to one, a simple kriging (SK) is performed. This is based on the assumption that the
global mean grade is respectively known and equal to m, and gives the following
expression:
Z m Z m
V
SK SK
=

( )

m
SK
=
1 represents the weight associated to the global mean.

It can be shown that OK is exactly the same as SK when m is replaced by its kriged
estimation. Thus, the coefficient
m
for a given neighbourhood gives us a clear
idea of the quality of kriging.
The larger
m
, the larger the neighbourhood should be, making the calculation
more time consuming and the resulting estimation smoother.
4. Distribution of weights.
The kriging weights should be very small, or even slightly negative, at the margins
of the search. Negative weights are not problematic if they represent a small
proportion of total weight.
How t o Look at t he Result s of a Kriging
There are several important steps when examining the output from a kriging (most
of these are good practice regardless of the estimation methodology):
Make maps of t he est i mat es
These should be level by level, section by section. Maps of the estimates must be
on the same scale as the drilling data. This will facilitate checking of results. Maps
should have the estimate and kriging variance, and are easier to use if they're colour
coded. A few well chosen cut offs for colour coding are better for checking
purposes than a large number of confusing colours.
In the view of the authors, limiting this step to examination of the results on
computer screens is poor practice (although such examination is a valuable
adjunct).
Negat i ve Wei ght s
A small number of negative
kriging weights at the
margins of the search are
not problematic.

199

Check t he l ocat i on of very hi gh and very l ow est i mat es
Check the location of very high and very low estimates in relation to the sample
data. This step is important, because gross errors in data can sometimes exist right
through to this late step (although they should not).
In addition, these very high estimates will disproportionately impact upon the
economics of the deposit, open pit optimisation, mine planning etc. Therefore, it's
important to get a good feel for their reliability.
Look careful l y at est i mat es near t he margi ns of t he deposi t .
Are these sensibly estimated? Have we respected geological boundaries?
Exami ne t he est i mat es i n t he cont ext of geol ogy.
Are the major interpreted features captured in the estimate (anisotropy for
example)? Remember that the resolution of the kriging (i.e. the block size) is
intended for mine planning and not geological description.
Look at t he kri gi ng vari ance i n rel at i on t o sampl i ng spaci ng.
The kriging variance is an index of sampling spacing. High
OK
2
will be associated
with the poorly sampled areas. Conversely, the lowest
OK
2
values will be associated
with the areas of highest sampling density.
Look at t he regressi on sl ope i n rel at i on t o sampl i ng spaci ng.
The kriging variance is an index of sampling spacing. Low slopes will be associated
with the poorly sampled areas. Conversely, the slope or equal to 1.0 will be
associated with the areas of highest sampling density, thus best estimation quality.
Exami ne t he est i mat es for poorl y sampl ed or unsampl ed areas.
Are these sensibly estimated?
The Pract ice of Kriging In Operat ing Mines
There are several particular subjects we will look at briefly in here to give a feel for
the application of geostatistics in exploration and mining situations.
Grade Cont rol
A common application of kriging is for grade control (or ore control) in an open
pit mine. We will consider here a few salient pointers to setting up and running a
geostatistical grade control procedure.
Why Kri gi ng?
This question has been answered by now, but it is worth restating bluntly: if the
grades have an appreciable spatial correlation, then kriging will be an improved
estimate (compared to IDW or polygons). In particular, polygonal methods (or
similar methods like IDW2 and IDW3) are quite unsuited to selective mining
control because they are highly conditionally biased. If the grades have little or no
spatial correlation (i.e. approach pure nugget) then local block estimation is
inadvisable.
Sel ec t i ve Mi ni ng
Polygonal methods (or
similar methods like IDW2
and IDW3) are quite
unsuited to selective mining
control because they are
highly conditionally biased.

200

This case of very poor, or no spatial correlation leaves us with few choices. The
polygonal method will perform even worse for this situation (because it assumes
very high spatial continuity) and is potentially disastrous! Our choices are:
1. Control selection by geology (if this is possible). If we can visually select ore
and waste (for example on the basis of colour) and the ore is payable en
masse then this is possible.
2. If we cannot separate ore and waste in the pit visually, then we must define
the outer boundaries of the mineralisation and bulk mine. If the average
grade is economic, this is feasible, if not, the project is uneconomic.
Geol ogy Fi rst !
Geostatistics must always be performed (as best as we can) within the boundaries
of known or interpreted geology. However, over-domaining, i.e. defining every
single lithological variant and structural domain as a stationarity domain, is poor
practice. A balance must be achieved: the smallest number of domains that
reasonably captures the grade variability/geology connection.
At grade control stage there is potentially far more geological knowledge, and thus
we have the opportunity to have excellent geological control. Unfortunately, there
are many examples of mines where mapping is not performed, or worse, the
mapping is done but never compiled and used. Blind grade control doesn't require
a geologist.
In any estimation, for grade control or earlier-stage resource estimation, the
domaining decisions (i.e. deciding on stationarity) are probably the most important
decisions made. Understanding geology plays a large part in such decisions.
Sampl i ng
The sampling geometry must be adapted to the geological and variographic
knowledge of the ore. For example, the anisotropy of the grid should resemble that
of the variograms. Further, the grid spacing should reflect the level of selectivity we
are trying to achieve.
The Vari ogram as a Tool
The variogram is a vital tool for the mine geologist. It assists with grid selection,
monitoring of sample preparation (via Co) and choosing the kriging
neighbourhood. Variograms should be calculated for sensible geological zones and
updated regularly. We should not be using the variogram calculated and fitted for
bench 1 when we are mining bench 15! We should be cautious of important
boundaries (oxide/sulphide, faults, significant geological contacts etc.) when
defining the zones we wish to use for variography.
Bl ock Est i mat i on
It's always advisable to use block kriging and not point kriging when estimating
resources. We should try to use sensible block sizes: in general, the blocks should
have minimum dimensions such that we have one block per blast hole sample on a
bench. Larger block dimensions will improve the reliability of estimates, but smaller
blocks will have increasingly high estimation variances.
Domai ni ng
Domaining is not entirely a
geological decision. We must
have a sufficient number of
samples in each domain to
infer the variogram for
example.

201

Determination of block size is part of Quantified Kriging Neighbourhood
Analysis, discussed earlier in this Chapter.
In the case of ditch-witch lines, the blocks should be centred on the lines (i.e. their
length in a direction perpendicular to the lines should be equal to the inter-line
spacing). In the direction parallel to the ditch witch lines, we should probably select
a block size using geological and mining selectivity criteria. Given a good
variogram, there is no reason that we should not have block dimensions equivalent
to the sampling interval along the lines. Of course, such an interval should
correspond to achievable mining selectivity in this direction.
Kri gi ng Techni que
In general, ordinary kriging performs very well in open cut mines and it is preferred
unless we have convincing reasons not to use it. If there are a significant number of
extreme values (for example in some gold deposits) we might consider a form of
modified kriging (using indicators for example). Note that the additional efficiency
of the estimator must be balanced against the consequent additional workload that
will be placed upon the mine staff.
Sometimes, if the extreme values are tightly geographically located (for example on
a mappable structure) we can remove the blocks containing the extreme values and
estimate these separately from the rest of the deposit.
Upper Cut s
Working with cut assays to determine the variogram is not generally advisable, but
cutting extreme values during estimation may still prove necessary. Cutting is less
necessary with an interpolator that smooths appropriately.
The determination of cuts should not be made by simple recipe, but rather on the
basis of assessment of the tenor and location of the extreme grades involved. How
much metal is involved? Are highest grades within high-grade areas, evenly
scattered? Is the mining method non-selective? In this last case, upper cutting may
not be necessary at all.

Bl oc k Si ze
Unless the nugget effect is
very low, and the ranges
very long, it is inadvisable to
estimate blocks significantly
smaller than the average grid
spacing.
202

10: Non-Linear
Est imat ion
It is impossible to know at the same time [at feasibility stage]
how much ore one has and where it is, but one can predict fairly
well the grade of large units and the proportion of ore and
waste within these units.
Michel David Geostatistical Ore Reserve Estimation 1977
Somet imes, Linear Est imat ion Isnt Enough
Many geostatistical variables have sample distributions that are highly positively
skewed. Because of this, significant de-skewing of the histogram and reduction of
variance occurs when going from sample to block support, where blocks are of
larger volume than samples.
When making estimates in both mining and non-mining applications we often wish
to map the spatial distribution on the basis of block support rather than sample
support. The SMU or selective mining unit in mining geostatistics refers to the
minimum support upon which decisions (traditionally: ore/waste allocation
decisions) can be made.
The SMU is usually significantly smaller than the sampling grid dimensions, in
particular at exploration/feasibility stages. Linear estimation of such small blocks
(for example by inverse distance weighting IDW or ordinary kriging OK)
results in very high estimation variances, i.e. the small block linear estimates have
very low precision.
A potentially serious consequence of the small block linear estimation approach is
that the grade-tonnage curves are distorted i.e. prediction of the content of an
attribute above a cut-off based on these estimates is quite different to that based on
true block values. Assessment of project economics (or other critical decision
making) based on such distorted grade-tonnage curves will be riskier than
necessary. While estimation of very large blocks, say similar in dimensions to the
Chapter
10
SMU
or selective mining unit in
mining geostatistics refers to
the minimum support upon
which decisions
(traditionally: ore/waste
allocation decisions) can be
made.

203

sampling grid, will result in lower estimation variance, it also implies very low
selectivity, which is often an unrealistic assumption.
This chapter presents an overview of the geostatistical approach to solving this
problem: non-linear estimation, drawing substantially in parts from the paper of
Vann and Guibal (2001).
Linear estimation is compared to non-linear estimation; the motivations of non-
linear approaches are presented. A summary of the main geostatistical non-linear
estimators is included.
In a non-linear estimation we estimate, for each large block (by convention called a
panel) the proportion of SMU-sized parcels above a cut-off grade or attribute
threshold. A series of proportions above cut-off defines the SMU distribution. Use
of such non-linear estimates reduces distortion of grade-tonnage curves and allows
for better decision-making.
A partial bibliography of key references on this subject is included in the references.
What is a Linear Int erpolat or ?
The General Idea
Inverse Distance Weighting (IDW) interpolators are linear, as is Ordinary Kriging
(OK). What do we mean by the term linear interpolator?
A relatively non-mathematical understanding of linear weighted averaging can be
gained from thinking about linear regression. In linear regression, the relationship
between two variables, x and y, is considered to be a straight line (i.e. linear). The
formula for this straight line is simple:
y ax b = +

Where a is the slope of the line and b is the value of y when x equals zero (i.e the y-
intercept). If we specify a particular value of x we can therefore conveniently
determine the expected y value corresponding to this x. It doesnt matter whether
we specify an x value which is very small or very large, or anywhere in-between: the
relationship between x and y is always the same the specified straight line. In
other words, the relationship used to estimate y does not alter as the magnitude of
the x value changes.
Panel
A large block, within which
the distribution of SMUs is
inferred.

204

The Exampl e of IDW
A linear interpolator has this property: the weights we assign to each of the N
sample locations inside our estimation neighbourhood are independent of the specific
data values at these locations. Think about the simplest kind of linear interpolator,
IDW. An IDW estimate assigns the weight to a sample located within the
estimation neighbourhood as:
=
=
N
j
j
i
i
d
d
1
1
1

Where are the weights, d are the distances from each sample location to the
centroid of the block to be estimated and is the power
33
. Once the power to be
used is specified, the i
th
sample is assigned a weight that depends solely upon its
location (distance d
i
to the centroid). Whether the sample at this location had an
average or extreme value does not have any impact whatsoever on the assignment
of .
Ordi nary Kri gi ng
OK is a more sophisticated linear interpolator proposed by Matheron (1962,
1963a, 1963b). OKs advantage over IDW as a linear estimator is that it ensures
minimum estimation variance given:
1. A specified model spatial variability (i.e. variogram or other characterisation
of spatial covariance/correlation), and
2. A specified data/block configuration (in other words, the geometry of the
problem).
The second criterion involves knowing the block dimensions and geometry, the
location and support of the informing samples, and the search (or kriging
neighbourhood) employed. Minimum estimation variance simply means that the
estimation error is minimised by OK.
Given an appropriate variogram model, OK will outperform IDW because the
estimate will be smoothed in a manner conditioned by the spatial variability of the
data (known from the variogram).
Non-Li near
Now, contrast linear regression with non-linear regression. There are many types of
non-linear relationships we can imagine between x and y, a simple example being:
y ax b = +
2

33
The denominator of this fraction expresses the weight calculated as a proportion of the total weight
allocated to all samples found within the search
Wei ght s
For linear interpolators, the
weights are independent of
the specific data values at
sample locations.

205

This is a quadratic (or parabolic) regression, available in most modern spreadsheet
software, for example. Note that the relationship between x and y is now clearly
non-linear the nature of the relationship between x and y is clearly dependent upon
the particular x value considered.
Non-linear geostatistical estimators therefore allocate weights to samples that are
functions of the grades themselves and not solely dependent on the location of
data.
Non-Linear Interpolat ors
Li mi t at i ons of Li near Int erpol at ors
The fundamental limitations of linear estimation (of which OK provides the best
solution) are straightforward:
We may be motivated to estimate the distribution rather than simply an expected
value at some location (or over some area/volume, if we are talking about block
estimation). Linear estimators cannot do this. The cases abound: recoverable ore
reserves in a mine, the proportion of an area exceeding some threshold of
contaminant content in an environmental mapping, etc.
1. We are dealing with a strongly skewed distribution, eg. a precious metal or
uranium deposit, and simply estimating the mean by a linear estimator (for
example by OK) is risky, the presence of extreme values making any linear
estimate very unstable. We may require knowledge of the distribution of
grades in order to get a better estimate of the mean. This usually involves
making assumptions about the distribution (for example, what is the shape
of the tail of the distribution?) even in situations where we are ostensibly
distribution free (for example using IK).
2. We may be studying a situation where the arithmetic mean (and therefore
the linear estimator used to obtain it) is an inappropriate measure of the
average, for example in situations of non-additivity like permeability for
petroleum applications or soil strength for geological engineering
applications.
The specific problem of estimating recoverable resources was the origin of non-
linear estimation and has been the main application.
From a geostatistical viewpoint, non-linear interpolation is an attempt to estimate
the conditional expectation, and further the conditional distribution of grade at a location,
as opposed to simply predicting the grade itself. In this case we wish to estimate the
mean grade (expectation) at some location under the condition that we know certain
nearby sample values (conditional expectation). This conditional expectation, with a few
special exceptions (eg. under the Gaussian Model see later) is non-linear.
In summary, non-linear geostatistical estimators are those that use non-linear
functions of the data to obtain (or approximate) the conditional expectation.
Wei ght s
For non-linear interpolators,
the weights are functions of
the specific data values at
sampled locations.
Obj ec t i ve
We wish to estimate the
mean grade (expectation) at
some location under the
condition that we know
certain nearby sample values.
This is called the
conditional expectation.

206

Obtaining this conditional expectation is possible, in particular through the
probability distribution:
[ ] Pr ( )| ( ) Z x Z x
o i

This reads: the probability of the grade at location x
o
given the known
sampling information at locations Z(x
i
) (i.e. Z(x
1
), Z(x
2
) .Z(x
N
). This is the
conditional distribution of grade at that location. Once we know (or approximate) this
distribution, we can predict grade tonnage relationships (eg. how much of this
block is above a cut-off Z
C
?).
Avai l abl e Met hods
There are many methods now available to make local (panel by panel) estimates of
such distributions, some of which are:
Disjunctive Kriging DK (Matheron, 1976, Armstrong and
Matheron, 1986a, 1986b);
Indicator Kriging IK (Journel, 1982, 1988) and variants
(Multiple Indicator Kriging; Median Indicator Kriging, etc.)
Probability Kriging PK (Verly and Sullivan, 1985);
Lognormal Kriging LK (Dowd, 1982);
Multigaussian Kriging MK (Verly and Sullivan, 1985,
Schofield, 1989a, 1989b);
Uniform Conditioning UC (Rivoirard, 1994, Humphreys,
1998).
Residual Indicator Kriging RIK (Rivoirard, 1989).
In a non-linear estimation we estimate, for each large block (by convention called a
panel) the proportion of SMU-sized parcels above a cut-off grade or attribute
threshold. A series of proportions above cut-off defines the SMU distribution.
Note that there is a very long literature warning strongly against estimation
of small blocks by linear methods (Armstrong and Champigny, 1989; David,
1972; David 1988; Journel, 1980, 1983, 1985; Journel and Huijbregts, 1978; Krige,
1994, 1996a, 1996b, 1997; Matheron, 1976, 1984; Ravenscroft and Armstrong,
1990; Rivoirard, 1994; Royle, 1979). By small blocks, we mean blocks that are
considerably smaller than the average drilling grid (say appreciably less than half the
size, although in higher nugget situations, blocks with dimensions of half the drill
spacing may be very risky).
The authors strongly reiterate this warning here. The prevalence of estimating
blocks that are far too small is symptomatic of misunderstanding of basic
geostatistics. Even estimating such small blocks directly by a non-linear estimator
may be incorrect and risky. When using non-linear estimation for recoverable
Smal l Bl oc k s
The prevalence of estimating
blocks that are far too small
is symptomatic of
misunderstanding of basic
geostatistics.

207

resources estimation in a mine, the panels should generally have dimensions
approximately equal to the drill spacing, and only in rare circumstances (i.e. strong
continuity) can significantly smaller panels be specified.
Note also that many programs allow the direct estimation of sub-cells and this is
not only theoretically incorrect, it has serious practical implications: the local error
of estimation will be unacceptable. The blocks estimated cannot be decreased in
size beyond that dictated by the information available. Any resultant increase in
local precision is entirely illusionary.
Non-linear estimation provides the solution to the small block problem. We cannot
precisely estimate small (SMU-sized) blocks by direct linear estimation. However,
we can estimate the proportion of SMU-sized blocks above a specified cut-off,
within a panel. Thus, the concept of change of support is critical in most practical
applications of non-linear estimation.
SUPPORT EFFECT
Defi ni t i on
Support is a term used in geostatistics to denote the volume upon which average
values may be computed or measured. Complete specification of support includes
the shape, size and orientation of the volume. If the support of a sample is very
small in relation to other supports considered, eg. drill hole sample upon which a
gold assay has been made, it is sometimes assumed to correspond to point
support. Support effect is the influence of the support on the distribution of
grades. Support is discussed extensively in preceding chapters.
The Necessi t y for Change of Support
Change of support is vital for predicting recoverable reserves if we intend to
selectively mine a deposit. Before committing the capital required to mine such a
deposit, an economic decision must be made based only on the samples available
from exploration drilling.
Because mining does not proceed with a selection unit of comparable size to the
samples, the difference in support between the samples and the proposed SMU
must be accounted for in any estimate to obtain achievable results. When there is a
large nugget effect, or an important short-scale structure apparent from the
variography, then the impact of change of support will be pronounced.
The histogram of drill hole samples will usually have a much longer tail than the
histogram of mining blocks. Simplistic variance corrections, for example affine
corrections, do not reflect the fact that, in addition to variance reduction, change of
support also involves symmetrisation of the histogram
34
. This is especially
important in cases where the histogram of samples is highly skewed.

34
This symmetrisation can be demonstrated via the central limit theorem of classical statistics, which
states that the means of repeated samplings of any distribution will have a distribution which is normal,
Smal l Bl oc k s (2)
Blocks cannot be decreased
in size beyond that dictated
by the information available.
Any resultant increase in
local precision is entirely
illusionary.

208

Recoverabl e Resources
Recoverable resources are the proportion of in-situ resources that are recovered
during mining. The concept of recoverable resources involves both technical
considerations, such as cut-off grade, SMU definition, machinery selection etc., and
also economic/financial considerations such as site operating costs, commodity
prices outlook, etc. In this chapter, only technical factors are considered.
Recoverable resources can be categorised as either global or local recoverable
resources. Global recoverable resources are estimated for the whole field of
interest; eg. estimation of recoverable resources for the entire orebody (or a large
well-defined subset of the orebody like an entire bench)
35
. Local recoverable
resources are estimated for a local subset of the orebody; eg. estimation of
recoverable resources for a 25mx50mx5m panel.
A Summary of Main Non-Linear Met hods
Indi cat ors
The use of indicators is a strategy for performing structural analysis with a view to
characterising the spatial distribution of grades at different cut-offs. The
transformed distribution is binary, and so by definition does not contain extreme
values. Furthermore, the indicator variogram for a specified cut-off z
c
is physically
interpretable as characterising the spatial continuity of samples with grades
exceeding z
c
.
Indicator transformations may thus be conceptually viewed as a digital contouring
of the data. They give very valuable information on the geometry of the
mineralisation.
A good survey of the indicator approach can be found in the papers of Andre
Journel (eg. 1983, 1987, 1989).
An indicator random variable ) , (
c
z x I is defined, at a location x , for the cut-off
c
z as the binary or step function that assumes the value 0 or 1 under the following
conditions:
I x z Z x z
I x z Z x z
c c
c c
( , ) ( )
( , ) ( )
=
= >
0
1
if
if

regardless of the underlying distribution.. When we consider block support, the aggregation of points to
form blocks will thus deskew the histogram. In the ultimate case, we have a single block, being the
entire zone of stationarity and there is no skewness as such.
35
Global recoverable resources can be very useful as checks on local recoverable estimation, a good first
pass valuation or can be used for checking the impact on grade-tonnage relationships of changing SMU,
bench-height studies, etc. They are not specifically discussed in this paper. The interested reader is
referred to Vann and Sans (1995).
Rec over abl e
Resour c es
This is a geostatistical term,
defined in the text. It is not a
JORC term.
I ndi c at or s
May be conceptually viewed
as a digital contouring of the
data. They give very valuable
information on the geometry
of the mineralisation.

209

The indicators thus form a binomial distribution, and we know the mean and
variance of this distribution from classical statistics:
m p
p p
=
=
2
1 ( )

Where p is the proportion of 1s as defined above (for example, if the cut-off, z
c
is
equal to the median of the grade distribution, p takes a value of 0.5, and the
maximum variance is defined as 0.25).
After transforming the data, indicator variograms can be calculated easily by any
program written to calculate an experimental variogram. An indicator variogram is
simply the variogram of the indicator.
Indi cat or kri gi ng
Indicator kriging (IK) is kriging of indicator-transformed values using the
appropriate indicator variogram as the structural function. In general the kriging
employed is ordinary kriging. (OK). An IK estimate (i.e. kriging of a single
indicator) must always lie in the interval [0,1], and can be interpreted either as
(1) probabilities (the probability that the grade is above the specified indicator) or
(2) as proportions (the proportion of the block above the specified cut-off on data
support).
In addition to its uses for indicator kriging, multiple indicator kriging (MIK),
probability kriging (PK) and allied techniques, the indicator variogram can be useful
when making structural analysis to determine the average dimensions of
mineralised pods at different cut-offs. Indicators are also useful for charactering the
spatial variability of categorical variables (eg. presence or absence of a specific
lithology, alteration, vein type, soil type, etc.).
Mul t i pl e Indi cat or kri gi ng
Multiple indicator kriging (MIK) involves kriging of indicators at several cut-offs
(see various publications by Andre Journel in the references as well as Hohn, 1988
and Cressie, 1993). MIK is an approach to recoverable resources estimation that is
robust to extreme values and is practical to implement. Theoretically, MIK gives a
worse approximation of the conditional expectation than disjunctive kriging (DK),
which can be shown to approximate a full cokriging of the indicators at all cut-offs,
but does not have the strict stationarity restriction of DK.
The major difficulties with MIK are discussed in detail by Vann, Guibal and Harley
(2000) and can be summarised as:
1. Order relation problems: i.e. because indicator variogram models may be
inconsistent from one cut-off to another we may estimate more recovered
metal above a cut-off z
c2
than for a lower cut-off z
c1
, where z z
c c 1 2
< ,
which is clearly impossible in nature. While there is much emphasis on the
triviality of order relation problems and the ease of their correction in the
literature, the authors have observed quite severe difficulties in this regard
with MIK. The theoretical solution is to account for the cross-correlation
I K
Indicator kriging is simply
kriging of indicators.

210

of indicators at different cut-offs in the estimation by cokriging of
indicators, but this is completely impractical from a computational and
time point of view. In fact, the motivation for developing probability
kriging (PK) was to approximate full indicator cokriging (see below).
2. Change of support is not inherent in the method. In the authors
experience, most practical applications of MIK involve using the affine
correction, which assumes that the shape of the distribution of SMUs is
identical to that of samples, the sole change in the distribution being
variance reduction as predicted by Kriges Relationship. There are clear
warnings in the literature (by Journel, Isaaks and Srivastava, Vann and
Sans, and others) about the inherent deskewing of the distribution when
going from samples to blocks. The affine correction is not suited to
situations where there is a large decrease in variance (i.e. where the nugget
is high and/or there is a pronounced short-scale structure in the variogram
of grades). Other approaches can be utilised, e.g. lognormal corrections
(very distribution dependent), or conditional simulation approaches (costly
in time). A new proposal for change of support in MIK is given by
Khosrowshahi et al. (1998).
Medi an Indi cat or Kri gi ng
Median indicator kriging is an approximation of MIK which assumes that the
spatial continuity of indicators at various cut-offs can be approximated by a single
structural function, that for m z
c
~
= , where
~
m is the median of the grade
distribution. The indicator variogram at (or close to) the median is sometimes
considered to be representative of the indicator variograms at other cut-offs.
This may or may not be true, and needs to be checked.
The clear advantage of median indicator kriging over MIK is one of time (both
variogram modelling and estimation). The critical risk is in the adequacy of the
implied approximation. If there are noticeable differences in the shape of
indicator variograms at various cut-offs, one should be cautious about using
median indicator kriging (Isaaks and Srivastava, 1989, pp 444). Hill et al (1998)
and Keogh and Moulton (1998) present applications of the method.
Probabi l i t y Kri gi ng
Probability kriging (PK) was introduced by Sullivan (1984) and a case study is given
in Verly and Sullivan (1985). It represents an attempt to alleviate the order
relationship problems associated with MIK, by considering the data themselves
(actually their standardised rank transforms, distributed in [0,1]) in addition to the
indicator values. Thus a PK estimate is a cokriging between the indicator and the
rank transform of the data U.
When performed for n cut-offs, it requires the modelling of 2n+1 variograms: n
indicator variograms, n cross-variograms between indicators and U, and finally the
variogram of U. The hybrid nature of this estimate as well as the time-consuming
complexity of the structural analysis makes it rather unpractical.

211

Indi cat or Cokri gi ng and Di sj unct i ve Krigi ng
In general, any practical function of the data can be expressed as a linear
combination of indicators:
) , ( ) (
n
n
n
z Z I f Z f

=
Thus, estimating ) (Z f amounts to estimating the various indicators. The best
linear estimate of these indicators is their full cokriging, which takes into account
the existing correlations between indicators at various cut-offs.
Full indicator cokriging (also called Disjunctive Kriging, abbreviated to DK)
theoretically ensures consistency of the estimates (reducing order relationships to a
minimum or eliminating them altogether): this makes the technique very appealing,
but there is a heavy price to pay: if n indicators are used, n
2
variograms and cross-
variograms need to be modelled, and this is unpractical as soon as n gets over 5 or
6, even with the use of modern automatic variogram modelling software.
The various non-linear estimation methods can be considered as ways of
simplifying the full indicator cokriging. Roughly speaking, there are three possible
paths to follow (Rivoirard, 1994):
1. Ignore the correlations between indicators: this is the choice made by MIK
already discussed. The authors consider this a fairly drastic choice.
2. Assume that there is intrinsic correlation, i.e.that all variograms and cross-
variograms are multiples of one unique variogram. In that case, cokriging is
strictly equivalent to kriging; this is the hypothesis underlying median IK.
Needless to say, unfortunately, this very convenient assumption is rarely
true in practice (see median IK, above).
3. Express the indicators as linear combinations of uncorrelated functions
(orthogonal functions), which can be calculated from the data. Cokriging of the
indicators is then equivalent to separate kriging of the orthogonal
functions; this decomposition of the indicators is the basis of residual
indicator kriging (RIK) and of isofactorial disjunctive kriging.
Resi dual Indi cat or Kri gi ng
In this particular model, within the envelope defined by a low cut-off, the higher
grades are randomly distributed. The proximity to the border of the envelope has
no direct incidence on the grade, and this corresponds to some types of vein
mineralisation, where there is little correlation between the geometry of the vein
and the grades. The validity of the model is tested by calculating the ratios
ij
i
h
h
( )
( )

(cross-variograms of indicators over variograms of indicator) for the cut-offs z
j

higher than z
i
. If these ratios remain approximately constant, then the model is
appropriate. Note that an alternative decreasing model exists where one
compares the cross-variograms to the variogram associated with the highest cut -
off (instead of the lowest ).

212

The residuals are defined from the indicator functions by:
1
1
) ), ( ( ) ), ( (
) (
=
i
i
i
i
i
T
z x Z I
T
z x Z I
x H where [ ] ) ), ( (
i i
z x Z I E T =
i.e. the proportion of grades higher than the cut-off z
i
.
i.e.
H x
0
1 ( ) =
1
) ), ( (
) (
1
1
1
=
T
z x Z I
x H
......
1
1
) ), ( ( ) ), ( (
) (
=
n
n
n
n
n
T
z x Z I
T
z x Z I
x H
The H x
i
( ) are uncorrelated and we have:
) (
) ), ( (
0
x H
T
z x Z I
i
j
j
i
i
=
=
This means that the indicators can be factorised. In order to get a disjunctive
estimate of )) ( ( x Z f , it is enough to krige separately each of the residuals H x
i
( ).
The T
i
are simply estimated by the means of the indicators, ) ), ( (
i
z x Z I .
In practice, the residuals are calculated at each data point, their variograms are then
evaluated and independent krigings are performed. Another check of the model
consists in directly looking at the cross variograms of the residuals: if they are flat,
indicating no spatial correlation, the model works. Thus, essentially this model
requires no more calculations than indicator kriging, while being more consistent
when it is valid.
The reader is referred to Rivoirard (1994, chapter 4) for a fuller explanation and a
case study (chapter 13) of this approach.
Residual indicators is one way to co-krige indicators by separately kriging
independent combinations of them and recombining these to form the co-kriged
estimate. Like MIK, this method involves working with many indicators and the
same number of variograms. Thus, it can be time consuming.
ISOFACTORIAL Di sj unct i ve Kri gi ng
There are several versions of isofactorial DK, by far the most common is Gaussian
DK.
Gaussian DK is based on an underlying diffusion model (where, in general, grade
tends to move from lower to higher values and vice versa in a relatively continuous
way).

213

The initial data are transformed into values with a Gaussian distribution, which can
easily be factorised into independent factors called Hermite polynomials (see
Rivoirard, 1994 for a full explanation and definition of Hermite polynomials and
disjunctive kriging). In fact, any function of a Gaussian variable, including
indicators, can be factorised into Hermite polynomials. These factors are then
kriged separately and recombined to form the DK estimate.
The major advantage of DK is that you only need to know the variogram of the
Gaussian transformed values in order to perform all the krigings required. The
basic hypothesis made is that the bivariate distribution of the transformed values is
bigaussian, which is testable. Although order relationships can occur, they are very
small and quite rare in general. A very powerful and consistent change of support
model exists for DK: the discrete Gaussian model (see Vann and Sans, 1995).
Gaussian disjunctive kriging has proved to be relatively sensitive to stationarity
decisions, (in most cases simple kriging is used in the estimation of the
polynomials). DK should thus only be applied to strictly homogeneous zones.
Uniform Condi t i oni ng
Uniform conditioning (UC) is a variation of Gaussian DK more adapted to
situations where the stationarity is not very good (i.e. typical mining situations
where intrinsic stationarity can be assumed but not strict stationarity.).
In order to ensure that the estimation is locally well constrained, a preliminary
ordinary kriging of relatively large panels is made, and the proportions of ore per
panel are conditional to that kriging value.
UC is a relatively robust technique. However, it does depend heavily upon the
quality of the kriging of the panels. As for DK, the discrete Gaussian model
ensures consistent change of support. Humphreys (1998) gives a case study of
application of UC to a gold deposit.
Lognormal Kri gi ng
Lognormal kriging (LK) is not linked to an indicator approach and belongs to the
conditional expectation estimates.
If the data are truly lognormal, then it is possible, by taking the log, and assuming
that the resulting values are multigaussian, to perform a lognormal kriging. The
resulting estimate is the conditional expectation and is thus in theory the best
possible estimate. This type of estimation has been used very successfully in South
Africa. Unfortunately the lognormal hypothesis is very strict: any departure can
result in completely biased estimates.
Mul t i gaussi an Kri gi ng
A generalisation of the lognormal transformation is the Gaussian transformation
that applies to any reasonable initial distribution. Again, under the multigaussian
hypothesis, the resulting estimate represents the conditional expectation and is thus
optimal. This is a very powerful estimate much more largely applicable than
lognormal kriging, but requires very good stationarity to be used with confidence.

214

Compared to Gaussian DK, multigaussian kriging is completely consistent, but
based on stronger multigaussian assumptions and its application to block
estimation is more complex.

Conclusions & Recommendat ions
After nearly 40 years since Matherons pioneering formulation of the Theory of
Regionalised Variables, there are a large number of operational non-linear
estimators to choose from. Understanding the underlying assumptions and
mathematics of these methods is critical to making informed choices when
selecting a technique.
1. We join the tedious chorus of geostatisticians over many years and
recommend that linear estimation of small blocks be consigned to the past,
unless it can be explicitly proved through very simple and long known
kriging tests that such estimation is adequate. It is our professional
responsibility to change to culture of providing what is asked for
regardless of the demonstrable and potentially serious financial risks of
such approaches. Small block OK or IDW estimates should no longer be
acceptable as inputs to important financial decisions.
2. A particular non-linear method is often applied by a given practitioner
without considering, for the data set in hand, whether the main
assumptions of that method are realistic. Some of these assumptions may
be testable, for example assumptions about the cross correlations of
indicators or assumptions about the nature of edge effects. Testing of
such assumptions is rarely performed, in our experience. We therefore
recommend that such tests be implemented (see Rivoirard, 1994).
3. The issue of change of support is critical in estimation of recoverable
resources, and as such should remain a major topic in our field. The major
criticisms of MIK, the most widely applied non-linear estimation method
in Australia, have centred on change of support (as pointed out by Glacken
and Blackney, 1998). The whole problem of recoverable reserves is the problem of
change of support. We recommend that practitioners become highly familiar
with the issue of change of support and bring a sophisticated appreciation
of this problem to their practice.
4. Conditional simulation (another non-linear method) is now within the
abilities of inexpensive desktop computing, leading to another possible
future route to recoverable resources. For a given block, the average of a
set of n conditional simulations is exactly equal to the kriged estimate of that block
In fact, as the full conditional distribution of the block grade is accessible,
any non linear estimate can be calculated. Now, it must be clear that
simulations are based exactly on the same type of hypotheses as most non-
linear estimation methods (stationarity, representativity of the variogram,
etc.) and, from this viewpoint, they need to be assessed as critically as any

215

estimation method. Multiple conditional simulation, by virtue of the
exponential increase in computational speed witnessed in the past decade,
is now becoming viable.
5. We hope that geostatistics does not go down a proprietary route. By this
we mean that the algorithmic basis of geostatistical methods should rightly be
in the public domain (and thus debatable and open to cross-validation).
The publication of GSLIB (Journel and Deutsch, 1998) sets standards in
this regard. Publication of actual source codes is more debatable of course,
and there is certainly no consensus about it.

216

11: Simulat ion
This chapter is in preparation
Tit le
text

Chapter
11

217
References
The following references include all those referred to in the text of this course, and
a selection of the large (and growing) bibliography of geostatistics.
Armstrong, M., 1984. Common problems seen in variograms. Mathematical
Geology, Vol. 16, No. 3, pp.305-313.
Armstrong, M., 1987. Coal mining geostatistics short course. Department of
Mining and Metallurgical Engineering, University of Queensland (St. Lucia), 102pp.
Armstrong, M., 1998. Basic linear geostatistics. Springer-Verlag (Berlin), 256pp.
Armstrong, M., (Ed.), 1989. Geostatistics Volumes 1 and 2 (Proc. of the 3rd. Int.
Geostatistical Congress at Avignon). Kluwer Academic Publishers (Dordrecht).
Armstrong, M. and Champigny, N., 1989. A study on kriging small blocks.
CIM Bulletin. Vol. 82, No. 923, pp.128-133.
Armstrong, M. and Dowd, P.A. (Eds.), 1994 Geostatistical Simulations. Kluwer
Academic Publishers, 260pp.
Armstrong, M., and Jabin, R., 1981. Variogram models must be positive-definite.
Mathematical Geology, Vol. 13, No. 5, pp.455-459.
Armstrong, M., and Matheron, G., 1986. Disjunctive kriging revisited: part I.
Armstrong, M., and Matheron, G., 1986. Disjunctive kriging revisited: part II.
Assibey-Bonsu, W., 1996. Summary of present knowledge on representative
sampling of ore in the mining industry. Journal of the South African Institute of Mining
and Metallurgy, November 1996, pp.289-293.
Baafi, E.Y., and Schofield, N.A., (Eds.), 1997. Geostatistics Wollongong 96,
Volumes 1 and 2 (Proc. of the 5th. Int. Geostatistical Congress at Wollongong).
Kluwer Academic Publishers (Dordrecht).
Beltrami, E., 1999. What is random? Chance and order in mathematics and life.
Copernicus/Springer-Verlag (New York) 201pp.

218
Bird, R., and Archer, W., 1987. Ditch WitchingA simple, but effective method
for open pit sampling developed in the WA Goldfields. International Mining
December, 1987, pp.20-21.
Cathles, L.M., 1981. Fluid flow and genesis of hydrothermal ore deposits. Economic
Geology 75th Anniversary Volume, pp. 424-457.
Clark, W.A.V., and Hosking, P.L., 1986. Statistical methods for geographers.
John Wiley & Sons (New York). 518pp.
Coleou, T., 1989. Cut off grade optimisation: a panacea or a fools paradise? in:
Geostatistics Volume 2 (Proc. of the 3rd. Int. Geostatistical Congress at Avignon). (Ed. M.
Armstrong), Kluwer Academic Publishers (Dordrecht), pp.889-900.
Cressie, N., 1993. Statistics for spatial data (Revised Edition). John Wiley and
Sons (New York), 900pp.
Cressie, N. and Hawkins, D.M., 1980. Robust estimation of the variogram.
David, M., 1972. Grade tonnage curve: use and misuse in ore reserve estimation.
Trans. IMM, Sect. A., Vol. 81, pp.129-132.
David, M., 1977. Geostatistical ore reserve estimation. Developments in
Geomathematics 2. Elsevier (Amsterdam), 364pp.
David, M., 1988. Handbook of applied advanced geostatistical ore reserve
estimation. Developments in Geomathematics 6. Elsevier (Amsterdam), 216pp.
Davis, J.C., 1986. Statistics and data analysis in geology (2nd Edition). John Wiley
& Sons (New York). 646pp.
de Fouquet, C., 1993. Simulation conditionnelle de fonctions alatoires: cas
gaussien stationnaire et schma linaire. Course notes C-151 - Centre de
Gostatistique (Fontainebleau).
Delfiner, P., 1979. Basic introduction to geostatistics. Centre de Geostatistique
(Fontainebleau) course CGMM-C78.
Deutsch, C.V., and Journel, A.G., 1992. GSLIB Geostatistical Software Library
and Users Guide. Oxford University Press, 340pp.
Deutsch, C.V., and Lewis, R. W., 1992. Advances in the practical
implementation of indicator geostatistics. Proceedings of the 23rd APCOM, Port City
Press (Baltimore) pp169-179
Dimitrakopoulos, R., (Ed.), 1994. Geostatistics for the next century. ( Proc. of an
international Forum in M. Davids Honour ) Kluwer Academic Publishers
(Dordrecht).
Dowd, P.A., 1982. Lognormal kriging the general case. Mathematical Geology, Vol.
14, No. 5, pp. 475-489.

219
Dowd, P.A., 1992. A review of recent developments in geostatistics. Computers and
Geosciences, Vol. 17, No. 10, pp. 1481-1500.
Feller, W., 1968. An introduction to probability theory and its applications,
Volume 1. (3rd Edition). John Wiley (New York), 509pp.
Franois-Bongaron, D., 1991. Geostatistical determination of sample variances
in the sampling of broken ores. CIM Bulletin, 84(950):46-57.
Franois-Bongaron, D., 1992. The theory of sampling of broken ores, revisited:
an effective geostatistical approach for the determination of sample variances and
minimum sample masses. Proceedings of the XVth World Mining Congress (Madrid), May
1992.
Franois-Bongaron, D., 1993. The practice of the sampling theory of broken
ores. C.I.M. Bulletin, Vol. 86, No. 970, pp.75-81.
Franois-Bongaron, D., 1996. Modern sampling theory. Short course notes,
MRDI/Geoval (Perth), 210pp.
Franois-Bongaron, D., and Gy, P., 2001. The most common error in applying
Gys formula in the theory of mineral sampling, and the history of the liberation
factor. in: Mineral Resource and Ore Reserve Estimation The AusIMM guide to good
practice (Monograph 23), The Australasian Institute of Mining and Metallurgy
(Melbourne), pp. 67-72.
Freund, J.E. and Walpole, R.E., 1980. Mathematical statistics (3rd Edition).
Prentice Hall (New Jersey). 548pp.
Glacken, I.M., 1997. Change of support and use of economic parameters for
block selection. In: Baafi, E.Y., and Schofield, N.A., (Eds.), Geostatistics
Wollongong 96, Volumes 1 and 2 (Proc. of the 5th. Int. Geostatistical Congress at
Wollongong). Kluwer Academic Publishers (Dordrecht).
Gomez, M. and Hazen, S., 1970. Evaluation of sulphur and ash distribution in
coal seams by statistical response surface regression analysis. Report of
Investigation 7377, US. Bureau of Mines (Washington), 120pp.
Goovaerts, P. Geostatistics for Natural Resources Evaluation. Oxford University
Press. 484pp.
Guarascio, M., et al., 1975. Advanced geostatistics for the mining industry. (Proc.
'Geostat 75' Rome) NATO ASI Series C122. Reidel (Dordrecht).
Guarascio, M., Pizzul, C. and Bologna, F., 1989. Forecasting of selectivity. in:
Geostatistics Volume 2 (Proc. of the 3rd. Int. Geostatistical Congress at Avignon). (Ed. M.
Armstrong), Kluwer Academic Publishers (Dordrecht), pp.901-909
Guibal, D.,1987. Recoverable reserves estimation at an Australian gold project. in:
Matheron, G., and Armstrong, M., (Eds.), Geostatistical case studies. Reidel
(Dordrecht), pp. 149-168.

220
Guibal, D. 1990. Geostatistics for exploration and mining. Short Course Notes,
Australian Mineral Foundation (Adelaide), 208pp.
Guibal, D., 1996. Application of conditional simulation for mining. Short course
notes, Geoval (Perth), 63pp.
Guibal, D., 1996. Elements of multivariate geostatistics. Short course notes,
Geoval (Perth), 7pp.
Guibal, D., 2001. Variography, a tool for the resource geologist. in: Mineral Resource
and Ore Reserve Estimation The AusIMM guide to good practice (Monograph 23), The
Australasian Institute of Mining and Metallurgy (Melbourne), pp. 67-72.
Guibal, D.,, Humphreys, M., Sanguinetti, H. and Shrivastava, P., 1997.
Geostatistical conditional simulation of a large iron orebody of the Pilbara region in
Western Australia. In: Baafi, E.Y., and Schofield, N.A., (Eds.), Geostatistics
Wollongong).
Gy, P.M., 1982. Sampling of particulate materials, theory and practice (2nd
Edition). Elsevier (Amsterdam). 431pp.
Gy, P.M., 1992. The sampling of heterogeneous and dynamic material systems.
Elsevier (Amsterdam).
Gy, P.M., 1998. Sampling for analytical purposes. John Wiley (London), 150pp.
Hartley, J.S., 1994. Drilling (Tools and programme management. AA Balkema
(Rotterdam), 150pp.
Henstridge, J., 1998. Non-linear modelling of geological continuity. In: Vann, J.
(Ed.), Proceedings of a one day symposium: Beyond Ordinary Kriging. October 30th, 1998, Perth
Western Australia. Geostatistical Association of Australasia.
Hoel, P.G., 1972. Introduction to mathematical statistics (Fourth Edition). John
Wiley and Sons (New York), 409pp.
Hohn, M.E., 1988. Geostatistics and petroleum geology. Van Nostrand Reinhold
(New York), 264pp.
Hoover, H.C., 1909. Principles of mining valuation, organization and
administration. McGraw-Hill (New York), 199pp.
Humphreys, M., 1996. Choosing and exploration drillhole spacing: A case study
in an iron mine. In: Baafi, E.Y., and Schofield, N.A., (Eds.), Geostatistics
Wollongong).
Humphreys, M., 1998. Local recoverable estimation: A case study in uniform
conditioning on the Wandoo Project for Boddington Gold Mine. In: Vann, J.
(Ed.), Proceedings of a one day symposium: Beyond Ordinary Kriging. October 30th, 1998, Perth
Western Australia. Geostatistical Association of Australasia.

221
Ingamells, C.O., 1981. Evaluation of skewed exploration datathe nugget effect.
Geochimica et Cosmochimica Acta. Vol. 45:1209-1216.
Isaaks, E.H., 1989. Risk qualified mappings for hazardous waste sites: A case
study in distribution-free geostatistics. Master of Science thesis, Department of
Earth Sciences, Stanford University (Palo Alto).
Isaaks, E.H., and Srivastava, R.M., 1989. An introduction to applied
geostatistics. Oxford University Press (New York) 561pp.
Journel, A.G., 1980. The lognormal approach to predicting local distributions or
selective mining unit grades. Mathematical Geology, Vol. 12, No. 4, pp. 285-303.
Journel, A.G., 1982. The indicator approach to estimation of spatial data.
Proceedings of the 17th APCOM, Port City Press (New York), pp. 793-806.
Journel, A.G., 1983. Nonparametric estimation of spatial distributions.
Mathematical Geology, Vol. 15, No. 3, pp. 445-468.
Journel, A.G., 1985. Recoverable reserves the geostatistical approach. Mining
Engineering, June 1985, pp. 563-568.
Journel, A.G., 1987. Geostatistics for the environmental sciences. United States
Environmental Protection Agency Report (Project CR 811893), U.S.E.P.A. (Las
Vegas), 135pp.
Journel, A.G., 1988. New distance measures the route toward truly non-
Gaussian geostatistics. Mathematical Geology, Vol. 20, No. 4, pp. 459-475.
Journel, A.G., 1989. Fundamentals of geostatistics in five lessons. Short Course in
Geology: Volume 8. American Geophysical Union (Washington), 40pp.
Journel, A.G., and Deutsch, C.V., 1998. GSLIB Geostatistical software library
and users guide, Second Edition, Oxford University Press, New York.
Journel, A.G., and Huijbregts, Ch.J., 1978. Mining geostatistics. Academic Press
(London), 600pp.
Kim, Y.C., Myers, D.E., Knudsen, H.P., 1977. Advanced geostatistics in ore
reserve estimation and mine planning (practitioner's guide). Department of Mining
and Geological Engineering, University of Arizona (Tucson), 154pp.
Koch, G.S. and Link, R.F., 1971. Statistical analysis of geological data. Dover
(New York). 813pp.
Khosrowshahi, S., Gaze, R., and Shaw, W., 1998. A new approach to change of
support for multiple indicator kriging. In Vann, J. (Ed.), Proceedings of a one day
symposium: Beyond Ordinary Kriging. October 30th, 1998, Perth Western Australia.
Geostatistical Association of Australasia.
Kitanidis, P.K., 1997. Introduction to geostatistics Applications in
hydrogeology. Cambridge University Press (Cambridge), 249pp.

222
Kreyszig, E., 1983. Advanced engineering mathematics (Fifth Edition). John
Wiley and Sons (New York), 988pp.
Krige, D.G., 1951. A statistical approach to some basic mine valuation problems
on the Whitwatersrand. Journal of the Chemical, Metallurgical and Mining Society of South
Africa (Dec 1951, March, May July and August 1952).
Krige, D.G., 1994. An analysis of some essential basic tenets of geostatistics not
always practised in ore valuations. Proceedings of the Regional APCOM, Slovenia.
Krige, D.G., 1996a. A basic perspective on the roles of classical statistics, data
search routines, conditional biases and information and smoothing effects in ore
block valuations. Proceedings of the Regional APCOM, Slovenia.
Krige, D.G., 1996b. A practical analysis of the effects of spatial structure and data
available and accessed, on conditional biases in ordinary kriging. In: Baafi, E.Y., and
Schofield, N.A., (Eds.), Geostatistics Wollongong 96, Volumes 1 and 2 (Proc. of
the 5th. Int. Geostatistical Congress at Wollongong).
Krige, D.G., 1997. Block kriging and the fallacy of endeavouring to reduce or
eliminate smoothing. Proceedings of the Regional APCOM, Moscow.
Lantuejoul, Ch., 1988. On the importance of choosing a change of support model
for global reserves estimation. Mathematical Geology, Vol. 20, No. 8, pp. 1001-1019.
Lantuejoul, Ch., and Rivoirard, J., 1984. Une methode de determination
d'anamorphose. Centre de Geostatistique, Ecole Des Mines De Paris
(Fontainebleau) Report N-916, 45pp.
Lipton, I.T., Gaze, R.L., and Horton, J.A., 1998. Practical application of
multiple indicator kriging to recoverable resource estimation for the Ravensthorpe
lateritic nickel deposit. In Vann, J. (Ed.), Proceedings of a one day symposium: Beyond
Ordinary Kriging. October 30th, 1998, Perth Western Australia. Geostatistical Association
of Australasia.
Leithold, L., 1986. The calculus with analytic geometry (5th Edition). Harper and
Row (New York), 1329pp.
Mandel, J., 1984. The statistical analysis of experimental data (Second Edition).
Dover Publications (New York), 410pp.
Marechal, A., 1978. Gaussian anamorphosis models. Fontainebleau Summer School
Notes C-72, Centre de Morphologie Mathematique, (Fontainebleau).22pp.
Matheron, G., 1962.. Traite de geostatistique applique, Tome I. Memoires du
Bureau de Recherches Geologiques et Minieres. No. 14. Editions Technip (Paris).
Matheron, G., 1963a. Traite de geostatistique applique, Tome II: Le Krigeage.
Memoires du Bureau de Recherches Geologiques et Minieres. No. 24. Editions
Technip (Paris).

223
Matheron, G., 1963b. Principles of geostatistics. Economic Geology. Vol. 58,
pp.1246-1266.
Matheron, G., 1973. Le krigage disjonctif. Internal note N-360. Centre de
Geostatistique, Fontainebleau, 21pp.
Matheron, G., 1976. A simple substitute for conditional expectation: The
disjunctive kriging. In Guarascio, M., et. al. (Eds.), Advanced Geostatistics in the Mining
Industry. Proceedings of NATO A.S.I.. Reidel (Dordrecht), pp. 221-236.
Matheron, G., 1981. La selectivitie des distributions. Centre de Geostatistique,
Ecole Des Mines De Paris (Fontainebleau) Report N-686, 45pp.
Matheron, G., 1982. La destructuration des haute teneurs et le krigeage des
indicatrices. Centre de Geostatistique, Ecole Des Mines De Paris (Fontainebleau)
Report N-761, 33pp.
Matheron, G., 1984. Selectivity of the distributions and the second principle of
geostatistics in: Verly, G., et al., (Eds.) Geostatistics for natural resources characterisation,
Reidel Publishing Co. (Dordrecht), pp.421-433.
Matheron, G., and Armstrong, M., (Eds.), 1987. Geostatistical case studies.
Reidel (Dordrecht), pp. 149-168.
McCuaig, T.C., Vann, J., and Seymour, C., 2000. Dynamic links between
geology and the mining process. In: 4
th
International Mining Geology Conference, Coolum,
Queensland, 14-17 May, 2000. The Australasian Institute of Mining and Metallurgy
(Melbourne), pp. 187-194.
Mood, A.M., and Graybill, F.A., 1963. Introduction to the theory of Statistics
(Second Edition). McGraw Hill-Kogakusha (New York/Tokyo), 443pp.
Olea, R.A. (Ed.), 1991. Geostatistical glossary and multilingual dictionary.
International Association for Mathematical Geology, Studies in Mathematical Geology
Volume 3. Oxford University Press (New York), 177pp.
Pitard, F.F. 1990a. Pierre Gy's sampling theory and sampling practice.
Volume 1. CRC Press (Florida).
Pitard, F.F. 1990b. Pierre Gy's sampling theory and sampling practice.
Volume 2. CRC Press (Florida).
Ravenscroft, P.J., 1989. A comparison of selectivity in a number of South African
gold mines. in: Geostatistics Volume 2 (Proc. of the 3rd. Int. Geostatistical Congress at
Avignon). (Ed. M. Armstrong), Kluwer Academic Publishers (Dordrecht), pp.911-
922.
Ravenscroft, P.J., and Armstrong, M., 1990. Kriging of block models the
dangers re-emphasised. Proceedings of APCOM XXII, Berlin, September 17-21, 1990.
pp.577-587.

224
Rivoirard, J., 1987a. Computing variograms on uranium data. in: Matheron, G.,
and Armstrong, M., (Eds.), Geostatistical case studies. Reidel (Dordrecht), pp. 1-22.
Rivoirard, J., 1987b. Geostatistics for skew distributions. South African Short Course
Notes, C-131, Centre de Morphology Mathematique (Fontainebleau) 31pp.
Rivoirard, J., 1987c. Two key parameters when choosing the kriging
neighborhood. Mathematical Geology, Volume 19, No. 8., pp.851-856.
Rivoirard, J., 1993. Relations between the indicators related to a regionalised
variable. In: Soares, A. (Ed). Geostatistics Troia 92., pp. 273-286. Kluwer Academic
Publishers, Dortrecht.
Rivoirard, J., 1994. Introduction to disjunctive kriging and non-linear geostatistics.
Centre de Morphology Mathematique (Fontainebleau) 90pp.
Rouhani, S., Srivastava, R.M., Desbarats, A.J., Cromer, M.V., and Johnson,
A.I., 1996. Geostatistics for environmental and geotechnical applications. ASTM.
(West Conshohocken, PA), 280pp.
Royle, A.G., 1979. Estimating small blocks of ore, how to do it with confidence.
World Mining, April 1979.
Royle, A.G., 1987. A workshop course in geostatistics. Department of Mining and
Mineral Engineering, University of Leeds (Leeds).
Sans, H., and Blaise, J.R., 1987. Comparing estimated uranium grades with
production figures. in: Matheron, G., and Armstrong, M., (Eds.), Geostatistical Case
Studies. Reidel (Dordrecht), pp. 169-185.
Sans, H., and Martin, V., 1984. Technical parametrisation of uranium reserves to
be mined by open-pit method, in : Verly, G., et al. (Eds.) Geostatistics for natural
resources characterisation., Volume 2, Reidel Publishing Company (Dordrecht),
pp.1071-1085.
Schofield, N.A., 1989a. Ore reserve estimation at the Enterprise gold mine, Pine
Creek, Northern Territory, Australia. Part 1: structural and variogram analysis.
C.I.M. Bulletin, Vol. 81. No. 909, pp.56-61.
Schofield, N.A., 1989b. Ore reserve estimation at the Enterprise gold mine, Pine
Creek, Northern Territory, Australia. Part 2: the multigaussian kriging model.
C.I.M. Bulletin, Vol. 81. No. 909, pp.62-66.
Sichel, H.S., 1952. New methods in the statistical evaluation of mine sampling
data. Trans. Inst. Mining Metallurgy, 61:261-288.
Sinclair, A.J., 1984. Univariate analysis. in: Howarth, R.J. (Ed.) Statistics and data
analysis in geochemical prospecting. Handbook of Exploration Geochemistry, Vol. 2. Elsevier
(Amsterdam), pp.59-81.
Sinclair, A.J., 1986. Statistical interpretation of soil geochemical data. Reviews in
Economic Geology Volume 4, pp.97-115.

225
Soares, A.O., (Ed.), 1993. Geostatistics Troia 92, Volumes 1 and 2 (Proc. of the
4th. Int. Geostatistical Congress). Kluwer Academic Publishers (Dordrecht).
Stephenson, P.R., and Vann, J., 2000. Commonsense and good communication
in Mineral Resource and Ore Reserve estimation. in: Mineral Resource and Ore Reserve
Estimation The AusIMM guide to good practice (Monograph 23), The Australasian
Institute of Mining and Metallurgy (Melbourne), pp. 13-20.
Stone, J.G., and Dunn, P.G., 1994. Ore reserve estimates in the real world. Society
iof Economic Geologists Spec. Pub. No. 3. SEG (Fort Collins, Co.), 150pp.
Sullivan, J., 1984. Conditional recovery estimation through probability kriging
theory and practice. In: Geostatistics for natural resources characterisation, Part 1. Verly, G.
et al. (Eds.), Reidel (Dordrecht), pp.365-384.
Thompson, M., 1984. Control procedures in geochemical analysis. in: Howarth,
R.J. (Ed.) Statistics and data analysis in geochemical prospecting. Handbook of Exploration
Geochemistry, Vol. 2. Elsevier (Amsterdam), pp.40-58.
Thorn, C.E., 1988. An introduction to theoretical geomorphology. Unwin Hyman
(Boston), 247pp.
Vann, J., 1993. Geostatistical studies of the Enterprise Gold Mine, Pine Creek,
Northern Territory, Australia. Thesis submitted for the degree of Master of Science (Mining
Geostatistics). Department of Mining and Mineral Engineering, University of Leeds.
Vann, J., 1996. What is sampling errorand how can we decrease it? - The
case of RC drilling. In: Victorian Chamber of Mines University of Ballarat Victorian
Coarse Gold Deposit Symposium.

Vann, J. (Ed.), 1998. Proceedings of a one day symposium: Beyond Ordinary
Kriging. October 30th, 1998, Perth Western Australia. Geostatistical
Association of Australasia.

Vann, J., and Guibal, D., 2000. Beyond ordinary kriging An overview of
non-linear estimation. in: Mineral Resource and Ore Reserve Estimation The
AusIMM guide to good practice (Monograph 23), The Australasian Institute of
Mining and Metallurgy (Melbourne), pp. 249-256.

Vann, J., Guibal, D., and Harley, M., 2000. Multiple Indicator Kriging is
it suited to my deposit? in: 4
th
International Mining Geology Conference, Coolum,
Queensland, 14-17 May, 2000, The Australasian Institute of Mining and
Metallurgy (Melbourne) pp. 9-17.

Vann, J., and Sans, H., 1995. Global resource estimation and change of support
at the Enterprise gold mine, Pine Creek, Northern Territory Application of the
geostatistical Discrete Gaussian model. in: Proceedings of APCOM XXV Conference,
Brisbane, Queensland, 9-14 July, 1995, The Australasian Institute of Mining and
Metallurgy (Melbourne), pp. 171- 180.
Velleman, P.F., and Hoaglin, D.C., 1981. Applications, basics and computing of
exploratory data analysis. Duxbury Press (Boston), 354pp.

226
Verly, G., 1983. The multigaussian approach and its applications to the estimation
of local reserves. Mathematical Geology, Vol. 15, No. 2, pp. 259-286.
Verly, G.W., et al., 1984. Geostatistics for natural resources characterisation.
NATO ASI Series C122. Reidel (Dordrecht).
Verly, G.W., and Sullivan, J., 1985. Multigaussian and probability krigings-
application to the Jerrit Canyon deposit. Mining Engineering 37(6):568-574.
Wackernagel, H., 1995. Multivariate geostatistics. Springer-Verlag (Berlin), 256pp.
Webster, R. and Oliver, M.A., 1990. Statistical methods in soil and land resource
survey. Oxford University Press (New York), 316.

227

QG Course Manual January 2008 Version 5.1

Uploaded by

Document Information

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

QG Course Manual January 2008 Version 5.1

Uploaded by

Copyright:

Available Formats

A p p l i e d

1 represents the weight associated to the global mean.

You might also like