Professional Documents
Culture Documents
Acs Ipoh (Q
Uploaded by
Sathia KdmsOriginal Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Acs Ipoh (Q
Uploaded by
Sathia KdmsCopyright:
Available Formats
954/1 Mark Scheme Trial 2012
cychin 1 acs ipoh
1. The functions f and g are defined as
f : x
x
1
, x
g : x x ln , x
+
(a) State the ranges of f and g . [2 marks]
(b) If h is the composite function gof, find the function h. [2 marks]
(c) Show that h(x) + g(x) = 0. [1 mark]
1(a)
R
f
= {y : y > 0}
R
g
= {y : y }
B1
B1
(b)
gof(x) = g (
)
= ln(
) or ln x
M1
h : x ln x , x > 0 A1
(c) h (x) + g(x) = ln x + ln x
= 0
A1
[5]
2. (a) Given
=
|
.
|
\
|
0
3
1
i
i
p = ( )
=
+
10
3
3 1
j
j where p is a constant.
Find the value of p. [3 marks]
(b) Use the binomial theorem to expand
x
x
+
1
1
as a series of ascending powers of x up to and
including the term in x
2
, where x <1.
Hence, by substituting x =
10
1
, show that
200
663
11 ~ . [6 marks]
2(a)
{(
} = {
OR
( )
= 8 + 3{3 + 4 + 5 + . . . + 9 + 10}
B1
Either one
= 164
M1
p =
A1
(b)
( )
( )
= (
) (
()
()
)
= (
) (
()
()
)
M1M1
Correct binomial expansion
1 + x + x
2
A1
(
= (
1 +
+ (
)
3 (
B1
M1
A1
Subst. x =
[9]
954/1 Mark Scheme Trial 2012
cychin 2 acs ipoh
3 Matrices P, Q and R are
|
|
|
.
|
\
|
3 2 2
2 1 1
2 1 0
,
|
|
|
.
|
\
|
15 22 8
3 8 7
33 34 14
and
|
|
|
.
|
\
|
2 6 2
3 3 3
6 6 6
respectively.
Find
12
1
PQR and deduce R
-1
. [4 marks]
Hence, solve the system of linear equations x + y z = 8
-4x +4 y +4 z = 0
x + 3y +z =10 [5 marks]
3
PQR = (
)(
)(
)
= (
)(
)
M1
Correct QR
= (
)
or
PQR = (
)(
)(
)
= (
)(
)
M1
Correct PQ
= (
)
PQR = (
)
A1
PQR = - 9 I
R
-1
= -
PQ
= -
(
)
=
(
M1
A1
By adjusting the system of linear equations : B1 Able to rearrange the system
of equations
(
)(
) (
)
B1
(
(
)(
)
M1
Reject all other methods.
= (
)
A1
x = 1, y = 4, z = -3 A1 [9]
954/1 Mark Scheme Trial 2012
cychin 3 acs ipoh
4 Given that the real numbers r and u , where r > 0 , - t u t < < ,
r cosu + 2r
2
cos2u + 3r
3
cos3u = 0 and r sinu + 2r
2
sin
2u + 3r
3
sin3u = 0.
By writing z = r (cosu + i sinu ) and using De Moivres Theorem, show that z = ) 2 1 (
3
1
i . [5 marks]
Determine the value of r and the two possible values of tanu . [4 marks]
4
r cosu + 2r
2
cos2u + 3r
3
cos3u = 0 (1)
r sinu + 2r
2
sin
2u + 3r
3
sin3u = 0. (2)
By operating (1) + i(2),
r (cosu + isinu ) + 2r
2
(cos2u + isin
2u ) + 3r
3
(cos3u + isin3u ) = 0
M1
r (cosu + isinu ) + 2r
2
(cosu + isinu )
2
+ 3r
3
(cosu + isinu )
3
= 0
M1 Using De Moivres
theorem
z + 2z
2
+ 3z
3
= 0 A1
OR z = r (cos + i sin )
z
2
= r
2
(cos 2 + i sin 2) and z
3
= r
3
(cos 3 + i sin 3) M1 Using De Moivres
theorem
2z
2
= 2r
2
(cos 2 + i sin 2) and 3z
3
= 3r
3
(cos 3 + i sin 3) M1
z + 2z
2
+ 3z
3
= 0 A1
z (3z
2
+ 2z + 1) = 0
z 0, z =
( )
M1
A1
| z | =
B1
tan =
(
or tan =
(
M1
tan = - tan =
A1A1 [9]
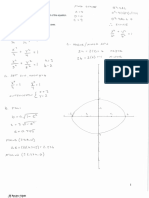
5 A curve has the parametric equations x = 8 cosu + 3 and y = 4 3 sinu where t u t s < .
Show that the curve is an ellipse and find its vertices, centre and foci. Sketch the ellipse. [9 marks]
5
By using cos =
and sin =
with sin
2
+ cos
2
= 1,
B1 Eliminating parameter
()
()
= 1
M1
Using trig. identity
()
= 1
the curve is an ellipse.
A1
Centre is (3, 0) A1
The vertices are (-5, 0) and (11, 0) A1A1
The foci are (7, 0) and (-1, 0) A1
954/1 Mark Scheme Trial 2012
cychin 4 acs ipoh
D1
D1
Ellipse shape (dependent on
the correct equation above)
All his points shown and
labeled.
[9]
6 Find the value of o for which the vectors a = 3i - 4j + k and b = i + 2j + o k are perpendicular.
Hence, find | a - b |. [4 marks]
6 By using a b = 0,
(
) (
) = 0
= 5
M1
A1
a - b = (
) - (
)
M1
= (
)
| a b | =
=
A1
Accept 7.48
[4]
7 (a) Solve for x the equation sin 2x = 3 cos
2
x, giving all solutions between 0
o
and 360
o
correct to
the nearest 0.1
o
. [5 marks]
(b) Express 2 cos x + 5 sin x in the form r cos ( x - ) o , where r >0 and 0<o < t
2
1
.
Hence, find the maximum value of 2 cos x + 5 sin x and the corresponding value of x in the
interval t 2 0 s s x . [6 marks]
Sketch the curve y = 2 cos x + 5 sin x for t 2 0 s s x . [2 marks]
By drawing an appropriate line on the graph, determine the number of roots of the equation
2 cos x + 5 sin x = 1, in the interval t 2 0 s s x . [2 marks]
7(a) 2sin x cos x - 3cos
2
x = 0 B1
cos x (2sin x - 3cos x) = 0 M1 Reject division by cos x
cos x = 0 or tan x =
M1
x = 90 , 270 or x = 56.3 , 236.3 A1
x = 56.3, 90 , 236.3 , 270 A1 All correct
(b)
2cos x + sin x r cos x cos + r sin x sin
r sin =
r cos = 2
B1 Both
r = 3, tan =
M1
x
y
(3, 0)
(7, 0)
(11, 0)
(-1, 0) (-5, 0)
(3, 4)
(3, - 4)
954/1 Mark Scheme Trial 2012
cychin 5 acs ipoh
r = 3, = 0.841 radians. A1 Both
2cos x + sin x = 3 cos (x 0.841)
A1
max value is 3 B1
when cos (x 0.841) = 1 x = 0.841radians. B1
D1
D1
M1
A cosine curve with a max.
and a min. turning point.
Initial and final points and
his max. point.
line y = 1
There are 2 roots. A1 Dependent on correct graph.
[15]
8 The line l has equation r =
|
|
|
.
|
\
|
+
|
|
|
.
|
\
|
0
1
2
5
0
5
, .
(a) Show that l lies in the plane whose equation is r . 5
0
2
1
=
|
|
|
.
|
\
|
. [3 marks]
(b) Find the position vector of A, the foot of the perpendicular from the origin O to l. [4 marks]
(c) Find an equation of the plane containing O and l. [4 marks]
(d) Find the position vector of the point P where l meets the plane t whose equation is r . . 11
2
2
1
=
|
|
|
.
|
\
|
[4 marks]
8(a)
r = (
) + (
) and r (
) = -5
By using r n = d,
(
) (
) = -5
B1
-5 2 + 2 = - 5 for all values of . M1
line l lies on the plane. A1
(b)
= (
) +
1
(
),
1
) = 0
(
) (
) = 0
B1
10 + 4
1
+
1
= 0 M1
y
x
3
2
-3
y = 1
(0.841, 3)
(2, 2)
954/1 Mark Scheme Trial 2012
cychin 6 acs ipoh
1
= -2
= (
) - 2(
)
= (
)
M1
A1
(c)
n =
)
= |
|
M1
= (
)
A1
equation of plane is r (
) = (
) (
)
r (
) = 0 or 5x + 10y + 5z = 0
M1
A1
Accept r (
) = 0
(d) Since P is on line l,
= (
) +
2
(
),
2
Given that r . . 11
2
2
1
=
|
|
|
.
|
\
|
(
) . . 11
2
2
1
=
|
|
|
.
|
\
|
B1
5 + 2
2
+ 2
2
+ 10 = 11 M1
2
= - 1 A1
= (
) - 1(
)
= (
)
A1
[15]
You might also like
- CSEC ADD Maths SPECIMEN PAPER 1 PDFDocument26 pagesCSEC ADD Maths SPECIMEN PAPER 1 PDFreeta ram100% (1)
- Fe Civil Math SolutionsDocument59 pagesFe Civil Math Solutionsegipcio852016No ratings yet
- Car Design TutorialDocument61 pagesCar Design TutorialNastase Costel100% (15)
- 5 6115930084000924535Document791 pages5 6115930084000924535situ sharmaNo ratings yet
- Trigonometric Ratios to Transformations (Trigonometry) Mathematics E-Book For Public ExamsFrom EverandTrigonometric Ratios to Transformations (Trigonometry) Mathematics E-Book For Public ExamsRating: 5 out of 5 stars5/5 (1)
- De Moiver's Theorem (Trigonometry) Mathematics Question BankFrom EverandDe Moiver's Theorem (Trigonometry) Mathematics Question BankNo ratings yet
- NUST Entry Test - Practice Test 3Document29 pagesNUST Entry Test - Practice Test 3Rahique ShuaibNo ratings yet
- Add Maths Monthly Test March 2016Document10 pagesAdd Maths Monthly Test March 2016Armadaramor ShiNo ratings yet
- GetStarted ESPRIT EnglishDocument182 pagesGetStarted ESPRIT EnglishRicardo CamposNo ratings yet
- Autocad CommandsDocument11 pagesAutocad CommandsHasnain Ashraf100% (1)
- MAT Paper 2015 SolutionsDocument9 pagesMAT Paper 2015 SolutionsXu SarahNo ratings yet
- Analytic Geometry: Graphic Solutions Using Matlab LanguageFrom EverandAnalytic Geometry: Graphic Solutions Using Matlab LanguageNo ratings yet
- InequalitiesDocument192 pagesInequalitiesEpic Win100% (2)
- CNC MillingDocument213 pagesCNC Millingedgar1707100% (1)
- UACE MATHEMATICS PAPER 1 2014 Marking GuideDocument14 pagesUACE MATHEMATICS PAPER 1 2014 Marking GuideSamuel HarvNo ratings yet
- STPM Mathematics T Past Year Question P1 P2 P3Document19 pagesSTPM Mathematics T Past Year Question P1 P2 P3Sou Voyage0% (3)
- Asme Aed-1-2023Document51 pagesAsme Aed-1-2023franz_passariniNo ratings yet
- 2014 2 NSEMBILAN SMKStPaul Seremban MATHS QADocument7 pages2014 2 NSEMBILAN SMKStPaul Seremban MATHS QASK100% (1)
- Series, Binomials, Logs, Counting Kopie 2Document23 pagesSeries, Binomials, Logs, Counting Kopie 2Dennis987No ratings yet
- Subject Review of IB 2023 Year - 1Document63 pagesSubject Review of IB 2023 Year - 1Duru SavdaNo ratings yet
- Differential Calculus - Das and Mukherjee (Chapter 15-21) PDFDocument119 pagesDifferential Calculus - Das and Mukherjee (Chapter 15-21) PDFArnab Dipra100% (2)
- SMK Kepong Baru Maths T P1 QNADocument9 pagesSMK Kepong Baru Maths T P1 QNAShu NeeNo ratings yet
- Topic 3 - Geometry and TrigonometryDocument52 pagesTopic 3 - Geometry and Trigonometry23493No ratings yet
- DPP (37-38) 11th J-Batch MathsDocument5 pagesDPP (37-38) 11th J-Batch MathsRaju SinghNo ratings yet
- Model Test Paper - 2 (Solved) : Maximum Marks: 90 Maximum Time: 3 HoursDocument10 pagesModel Test Paper - 2 (Solved) : Maximum Marks: 90 Maximum Time: 3 Hoursrita soniNo ratings yet
- Alevel C3C4Document59 pagesAlevel C3C4nuddin123No ratings yet
- Answer All Questionsin This Section. x+1 Marks)Document8 pagesAnswer All Questionsin This Section. x+1 Marks)Xue Yi LamNo ratings yet
- PENANG 2013 STPM TRIAL PAPERS For Mathematics T TERM 2Document8 pagesPENANG 2013 STPM TRIAL PAPERS For Mathematics T TERM 2SK100% (3)
- AA HL Paper 1 1Document46 pagesAA HL Paper 1 1SagarNo ratings yet
- 2014 2 MELAKA SMK Gajah Berang - MATHS QADocument6 pages2014 2 MELAKA SMK Gajah Berang - MATHS QASK67% (3)
- 2014 2 NSEMBILAN KGVseremban Maths QADocument7 pages2014 2 NSEMBILAN KGVseremban Maths QASK0% (1)
- Answer All Questions in This SectionDocument8 pagesAnswer All Questions in This SectionSK67% (3)
- Mathematical Methods Cas, Units 3 & 4 2009 Assignment 6 - Circular FunctionsDocument2 pagesMathematical Methods Cas, Units 3 & 4 2009 Assignment 6 - Circular FunctionsRayanNo ratings yet
- Review Exercise 2Document19 pagesReview Exercise 2eventra bangladeshNo ratings yet
- EMT 1101 End of Semester Supplementary Exam December 2015Document6 pagesEMT 1101 End of Semester Supplementary Exam December 2015jonathane nhlaneNo ratings yet
- Sekolah Tinggi Segamat Term 1 2020 Q&A Maths T STPMDocument14 pagesSekolah Tinggi Segamat Term 1 2020 Q&A Maths T STPMKeertana SubramaniamNo ratings yet
- Maths T Trial Sem 1 PCGHSDocument3 pagesMaths T Trial Sem 1 PCGHSKhor Han YiNo ratings yet
- Penang JitSin MathsT P1 2015 QADocument13 pagesPenang JitSin MathsT P1 2015 QAlingbooNo ratings yet
- Wing Hong Tony Wong: R R R 2RDocument5 pagesWing Hong Tony Wong: R R R 2RRich WongNo ratings yet
- 00 C3 Mock To June 10Document44 pages00 C3 Mock To June 10Nayantara GopiNo ratings yet
- Ibdp Maa SL Practice QuestionsDocument24 pagesIbdp Maa SL Practice QuestionsEmNo ratings yet
- STS Term 1 2021 (Q&A)Document12 pagesSTS Term 1 2021 (Q&A)Wendy LohNo ratings yet
- Name Student ID No Class S 2 S Date: 17-5-2016 0800 1000Document3 pagesName Student ID No Class S 2 S Date: 17-5-2016 0800 1000黄心怡No ratings yet
- Scheme of ValuationDocument20 pagesScheme of ValuationRaghu Nandan HukkardeNo ratings yet
- Trial Kelantan 2021 950/1Document11 pagesTrial Kelantan 2021 950/1ZurainiNo ratings yet
- Numbers and Algebra Factors and Multiples Classification of Whole NumbersDocument10 pagesNumbers and Algebra Factors and Multiples Classification of Whole NumbersHenry De Zhuang LiNo ratings yet
- Test 4 - SMKJT - Ques&AnsDocument10 pagesTest 4 - SMKJT - Ques&AnsLIM YEE WEN MoeNo ratings yet
- Be Computer Engineering Semester 3 2019 December Applied Mathematics III CbcgsDocument15 pagesBe Computer Engineering Semester 3 2019 December Applied Mathematics III CbcgsMadhura KanseNo ratings yet
- 2021-1-Me-Gbs (Q&a)Document8 pages2021-1-Me-Gbs (Q&a)rosmawatiNo ratings yet
- 2008 h2 Math Prelim p1 (Solns)Document19 pages2008 h2 Math Prelim p1 (Solns)Utsav NiroulaNo ratings yet
- Answer: 2019-2-Ns-St. Paul, Seremban Sectiona (45 Marks) All Questions in This SectionDocument6 pagesAnswer: 2019-2-Ns-St. Paul, Seremban Sectiona (45 Marks) All Questions in This SectionBryanLeeChienYungNo ratings yet
- Answer Allquestions in This Section.: Confidential Section A (45 Marks)Document4 pagesAnswer Allquestions in This Section.: Confidential Section A (45 Marks)Add Maths TeacherNo ratings yet
- TJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocument12 pagesTJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongNo ratings yet
- Segamat High 2018T2 TRIAL Section A (45 Marks) Answer All Questions in This SectionDocument10 pagesSegamat High 2018T2 TRIAL Section A (45 Marks) Answer All Questions in This SectionNorbert LimNo ratings yet
- Seminar 3 SolutionsDocument6 pagesSeminar 3 Solutionsarmaansinghgill05No ratings yet
- 2017 NS SpiDocument2 pages2017 NS SpiMasytah YazidNo ratings yet
- SPM 2012 - FullDocument27 pagesSPM 2012 - FullWong Weng SonNo ratings yet
- <!DOCTYPE HTML PUBLIC "-//W3C//DTD HTML 4.01 Transitional//EN" "http://www.w3.org/TR/html4/loose.dtd"> <HTML><HEAD><META HTTP-EQUIV="Content-Type" CONTENT="text/html; charset=iso-8859-1"> <TITLE>ERROR: The requested URL could not be retrieved</TITLE> <STYLE type="text/css"><!--BODY{background-color:#ffffff;font-family:verdana,sans-serif}PRE{font-family:sans-serif}--></STYLE> </HEAD><BODY> <H1>ERROR</H1> <H2>The requested URL could not be retrieved</H2> <HR noshade size="1px"> <P> While trying to process the request: <PRE> TEXT http://www.scribd.com/titlecleaner?title=C3_collated_2005-2008.pdf HTTP/1.1 Host: www.scribd.com Proxy-Connection: keep-alive Accept: */* Origin: http://www.scribd.com X-CSRF-Token: 8b0a4f12b18d125fd3859e5b60dbcf5028dce8f6 User-Agent: Mozilla/5.0 (Windows NT 6.1) AppleWebKit/537.31 (KHTML, like Gecko) Chrome/26.0.1410.64 Safari/537.31 X-Requested-With: XMLHttpRequest Referer: http://www.scribd.com/upload-document?archive_doc=51750686&metadaDocument14 pages<!DOCTYPE HTML PUBLIC "-//W3C//DTD HTML 4.01 Transitional//EN" "http://www.w3.org/TR/html4/loose.dtd"> <HTML><HEAD><META HTTP-EQUIV="Content-Type" CONTENT="text/html; charset=iso-8859-1"> <TITLE>ERROR: The requested URL could not be retrieved</TITLE> <STYLE type="text/css"><!--BODY{background-color:#ffffff;font-family:verdana,sans-serif}PRE{font-family:sans-serif}--></STYLE> </HEAD><BODY> <H1>ERROR</H1> <H2>The requested URL could not be retrieved</H2> <HR noshade size="1px"> <P> While trying to process the request: <PRE> TEXT http://www.scribd.com/titlecleaner?title=C3_collated_2005-2008.pdf HTTP/1.1 Host: www.scribd.com Proxy-Connection: keep-alive Accept: */* Origin: http://www.scribd.com X-CSRF-Token: 8b0a4f12b18d125fd3859e5b60dbcf5028dce8f6 User-Agent: Mozilla/5.0 (Windows NT 6.1) AppleWebKit/537.31 (KHTML, like Gecko) Chrome/26.0.1410.64 Safari/537.31 X-Requested-With: XMLHttpRequest Referer: http://www.scribd.com/upload-document?archive_doc=51750686&metadaMorounshayo OshodiNo ratings yet
- MATHEMATICS - (12th & 13th) Paper-2Document5 pagesMATHEMATICS - (12th & 13th) Paper-2Raju SinghNo ratings yet
- Determinant PrintDocument15 pagesDeterminant PrintPrincess EsmejardaNo ratings yet
- Monthly Test Aug 09 Add Maths Form 4Document5 pagesMonthly Test Aug 09 Add Maths Form 4Bid HassanNo ratings yet
- 2010 STPM Trial Exam QuestionsDocument16 pages2010 STPM Trial Exam Questionsxuanxuan92No ratings yet
- Maths Model Test Paper For Summative Assessment - 1Document13 pagesMaths Model Test Paper For Summative Assessment - 1Apex InstituteNo ratings yet
- 2015 2 Per Horley Methodist QaDocument8 pages2015 2 Per Horley Methodist QakartiniNo ratings yet
- LSE MA100 Background CheckDocument5 pagesLSE MA100 Background CheckAlternative EgoNo ratings yet
- 2004 State Mathematics Finals: Algebra I Solutions: C C XC X C XDocument5 pages2004 State Mathematics Finals: Algebra I Solutions: C C XC X C XbiswacementNo ratings yet
- 2018 1 NS Spi Q&aDocument8 pages2018 1 NS Spi Q&aXue Yi LamNo ratings yet
- Ordcirclesoln1998 PDFDocument3 pagesOrdcirclesoln1998 PDFGraham MooreNo ratings yet
- Ordcirclesoln 1998Document3 pagesOrdcirclesoln 1998Graham MooreNo ratings yet
- Integrated Mathematics 4: Updated 09/15/04Document16 pagesIntegrated Mathematics 4: Updated 09/15/04Neha SinghNo ratings yet
- Cad Lab ManualDocument48 pagesCad Lab ManualRiteshSharmaNo ratings yet
- FIITJEE - CM Monthly Test-4: Physics, Chemistry & MathematicsDocument24 pagesFIITJEE - CM Monthly Test-4: Physics, Chemistry & MathematicsArsh DhawanNo ratings yet
- HTI - Computer Graphics Course - LecDocument15 pagesHTI - Computer Graphics Course - Lecمحمود إبراهيمNo ratings yet
- Performance Task - Graphing Conic Sections - Student GuideDocument7 pagesPerformance Task - Graphing Conic Sections - Student GuideYisel Alexandra Monsalve HernandezNo ratings yet
- 137 Quiz 6 ClassworkDocument23 pages137 Quiz 6 ClassworkYuma ShonaiNo ratings yet
- TECHNICAL-DRAWING Paper 2 and 3Document15 pagesTECHNICAL-DRAWING Paper 2 and 3Morgan InyangNo ratings yet
- CG Lab ManualDocument30 pagesCG Lab ManualArpit BhargavaNo ratings yet
- Report of Square GearDocument9 pagesReport of Square GearsrajaprojectsNo ratings yet
- MCQ On 2d Transformation in Computer GraphicsDocument6 pagesMCQ On 2d Transformation in Computer Graphicsvishwajeet patilNo ratings yet
- 4 Kepler LabDocument4 pages4 Kepler LabJovie MedsNo ratings yet
- Composite Material Leaf SpringDocument25 pagesComposite Material Leaf Springpank1987_inNo ratings yet
- Pre-Calculus Quarter 1 Week 1 Module 1 Learning CompetenciesDocument9 pagesPre-Calculus Quarter 1 Week 1 Module 1 Learning CompetenciesGleynne MilloradaNo ratings yet
- MULTIPLE CHOICE QUESTIONS in ENGINEERING MATHEMATICS Besavilla, Jr. VOL1 PDFDocument122 pagesMULTIPLE CHOICE QUESTIONS in ENGINEERING MATHEMATICS Besavilla, Jr. VOL1 PDFRed RelozaNo ratings yet
- Stress Analysis of Different Reinforcement Pad For Nozzle Opening in Pressure VesselDocument7 pagesStress Analysis of Different Reinforcement Pad For Nozzle Opening in Pressure VesselIJSTENo ratings yet
- Desing Spillways Crest Reese-MaynordDocument15 pagesDesing Spillways Crest Reese-Maynordluisfernando1810No ratings yet
- Handbook Trade Industry 7theditionDocument1,344 pagesHandbook Trade Industry 7theditionvera82us9495100% (1)
- Engineering Drawing Questions and Answers - Basics of Section of SolidsDocument22 pagesEngineering Drawing Questions and Answers - Basics of Section of SolidsMANIKANDAN KNo ratings yet
- Precal Lesson 1Document7 pagesPrecal Lesson 1Srspc Flor MendozaNo ratings yet