B.

Sucuolu 1

5.

Seismic Analysis Procedures in Earthquake Codes



5.1 INTRODUCTION

Seismic analysis procedures in earthquake codes prescribe calculation of seismic
design forces. These procedures mainly comprise of the following steps:

1. Calculate lateral earthquake forces for linear elastic response.
2. Reduce linear elastic forces to account for inelastic response.
3. Apply the reduced forces to the structure and carry out structural analysis.
4. Determine the internal seismic design forces acting on structural members, and
combine them with the internal forces determined under gravity loads.
5. Design structural members under these combined design forces.

In Step 1, lateral earthquake forces are calculated from a linear elastic acceleration
response spectrum which represents design ground motion intensity. The linear
acceleration spectrum is reduced in Step 2 in order to account for the inelastic deformation
capacity (ductility) of the system. Then a structural model is constructed in Step 3, and
response spectrum analysis is carried out under the reduced acceleration spectrum (design
spectrum). Internal seismic design forces are determined in Step 4, and they are further
combined with the results of gravity analysis. Finally structural members are designed
under these combined force demands in Step 5. Hence, this is a force-based design
procedure since the design of structural members is based on internal forces which
indirectly account for the inelastic deformation capacity of the conceived structural system.
This deformation capacity has to be assumed in advance since the system has not been
designed yet.
Although the analytical development of the procedures introduced in this Chapter is
similar to the procedures discussed in Chapters 2 and 3, their format is presented in
conformance with the general code notation.
B. Sucuolu 2

5.2 DESIGN GROUND MOTIONS: LINEAR ELASTIC RESPONSE SPECTRUM

The design earthquake is expressed by a smooth linear elastic acceleration response
spectrum in seismic design codes. A smooth spectrum represents a statistical average of the
response spectra obtained for many ground motions with similar intensities, recorded on
similar sites. We may consider the mean spectrum of ground motions normalized with
respect to PGA in Fig. 2.18.b which are recorded on semi-stiff soils. This figure is repeated
below in Fig. 5.1 for convenience.









Fig. 5.1. Mean acceleration spectra of 10 ground motions normalized with respect to their peak
ground accelerations.

5.2.1 Linear Elastic Acceleration Spectrum in the Turkish Code

The normalized mean spectral curve in Fig. 5.1 can be approximated by a simple
smooth curve for design purposes. The smooth normalized mean spectral shape is
expressed by a generic spectrum shape in the 2007 Turkish Earthquake Design Code,
which is composed of three line segments. The generic normalized spectrum shape is
shown in Fig. 5.2.









Fig. 5.2. Normalized spectrum shape in the Turkish Seismic Code, 2007.
B. Sucuolu S

The three portions of the linear elastic acceleration spectrum in Fig. 5.2 are expressed by
S

(I) = _1 +1.S
I
I
A
] I < I
A

S

(I) = 2.S I
A
< I < I
B
(5.1)
S

(I) = 2.S [
1
B
1

0.8
I > I
B


Soil conditions at the site are represented by T
A
and T
B
in the Turkish Earthquake
Code which are defined in Table 5.1. As the soil conditions vary from very stiff to soft, it
is reflected in the spectrum shape by a longer plateau region. This approximation for
reflecting the effect of soil conditions on spectral shape is under strong criticism lately
since it is known that the amplification factor 2.S in Eq. (5.1) is also sensitive to the local
soil conditions.

Table 5.1. Corner periods for different soil conditions
Local Soil Conditions T
A
(s) T
B
(s)
Z1 (rock) 0.10 0.30
Z2 (stiff soil) 0.15 0.40
Z3 (soft soil) 0.15 0.60
Z4 (loose alluvium) 0.20 0.90


A comparison of the normalized spectrum of the Turkish Earthquake Code for Z2
soil type with the normalized spectrum in Fig. 5.1 is shown in Fig. 5.3. The agreement is
evident except at very small periods in the 0.10 second range where the Code spectrum is
more conservative.












Fig. 5.3. Normalized linear elastic acceleration spectrum in the Turkish Earthquake Code (2007)
for stiff soil conditions (Z2), compared with the normalized mean linear elastic acceleration spectra
from 10 ground excitations.
B. Sucuolu 4

When the normalized spectrum is scaled by the peak ground acceleration PGA
along the vertical axis and the structure importance factor I is applied, an absolute
spectrum is obtained. The absolute spectrum is expressed by Eq. 5.2 and plotted in Fig. 5.4
where PGA=A
0
g, g is the acceleration of gravity (9.81 m/s
2
), S

(I) is given in Eq. (5.1)
and T
A
and T
B
are the corner periods in Table 5.1.
S
uc
(I) = A
0
g I S

(I) (5.2)
The structure importance factor I in the above equation indirectly account for less
risk, or better expected performance specified for important structures. It increases the
seismic design forces by 1.5 for emergency facilities (hospitals, fire and police stations,
etc.), by 1.4 for schools and by 1.2 for stadiums, theatres and concert halls, compared to
the ordinary buildings. Accordingly these structures are designed for higher lateral
strength, and hence they are expected to sustain less damage under the design earthquake.
Emergency facilities (I =1.5) are expected to remain functional after a severe earthquake.








Fig. 5.4. Absolute linear elastic acceleration spectrum in the Turkish Seismic Code, 2007 (I=1).

The coefficient A
0
in Eq. 5.2 and in Fig. 5.4 is called the effective ground
acceleration coefficient. It is determined by the probabilistic seismic hazard analysis
(PSHA) procedure discussed in Chapter 4. A
0
is given in Table 5.2 for five different
seismic zones in Turkey. Five seismic zones in Table 5.2 were defined in the Seismic
Zone Map of Turkey shown in Fig. 4.12.

Table 5.2. Effective ground acceleration coefficient in the five seismic zones in Turkey
Seismic Zone 1 2 3 4 5
A

0.40 0.30 0,20 0.10 0.0
B. Sucuolu S

5.2 REDUCTION OF ELASTIC FORCES: DESIGN SPECTRUM

We have discussed earlier in Chapter 2 that linear elastic spectrum can be reduced
if inelastic response is permitted. The reduced inelastic acceleration response spectrum
S
ai
(T) can be directly obtained from the linear elastic acceleration response spectrum
S
ae
(T)through
S
u
(I) =
S
cc
(1)
R

(1)
(5.3)
by invoking Eq.(2.65.a). R

is the ductility reduction factor in the above equation, which

was introduced in Section 2.6.4. It is a function of both period and the ductility factor (see
Figures 2.28 and 2.29).
This force reduction concept for SDOF systems introduced in Chapter 2 can also be
applied to the MDOF systems which can be idealized as equivalent SDOF systems. Lets
consider a frame in Fig. 5.5 with inelastic deformation capacity, subjected to an increasing
lateral force distribution (static pushover analysis).







(a)









(b)





Fig. 5.5. An inelastic frame subjected to increasing static lateral forces (pushover analysis).
a) Incremental lateral forces and corresponding incremental lateral displacements, b) idealized
inelastic force-deformation (moment-curvature) characteristics of the yielding member ends.
B. Sucuolu 6

For each force distribution

, there is a corresponding displacement distribution u

i

obtained from nonlinear static analysis. The distribution of

can be taken similar to the

distribution of equivalent static first mode force distribution given by Eq. (3.50) with n=1,
but applied incrementally in small lateral load steps. The sum of lateral forces in

is the
base shear force V
bi
where I
b
= 1
1

, and the roof displacement at top is u

roof,i
at the ith
load step.
When the loading increments are applied progressively on the inelastic structure,
internal moments at certain sections will eventually reach the yield capacities shown in
Fig. 5.5.b, and these sections will enter the elasto-plastic response region. As further lateral
load increments are applied, such sections will not be able to develop additional resistance
and redistribute the internal forces that they cannot resist to other sections while they
exhibit plastic deformation. Hence, the number of plastic end regions (plastic hinges)
increase with increasing lateral loads, accompanied by reduction of lateral stiffness of the
system. The state of plastic hinge distribution at three different lateral load states is
depicted in Fig. 5.6.






Fig. 5.6. Plastic hinge distribution in an inelastic frame subjected to increasing static lateral forces
(pushover analysis) at three different loading states.

If we plot V
b
versus u
roof
, we obtain a capacity curve which resembles the force-
displacement relation of an equivalent SDOF inelastic system. Capacity curve for the
frame in Fig. 5.6 is shown in Fig. 5.7, and the lateral load states indicated in Fig. 5.6 are
also marked on the capacity curve.

B. Sucuolu 7













Fig. 5.7. Capacity curve of the inelastic frame obtained from pushover analysis.

Various strength levels are indicated on the capacity curve in Fig. 5.7. V
e
is the base
shear force demand from linear elastic structure by the earthquake ground motion which is
expressed by a linear elastic spectrum. V
y
is the yield base shear force or the base shear
capacity whereas V
d
is the presumed design base shear of the frame structure. We may now
introduce two ratios among these strength levels.

v
c
v
j
= R

: Ductility reduction factor (5.4)

v
j
v
d
= R
o
: Overstrength reduction factor (5.5)
Ductility reduction factor R

in Eq. (5.4) that is defined for an inelastic MDOF

system is identical to the ductility reduction factor introduced above in Eq. (5.3), and
previously in Chapter 2, for an inelastic SDOF system. The similarity between Fig. 5.7 for
an inelastic MDOF system and Fig. 2.27 for an ideal inelastic (elasto-plastic) SDOF
system is also evident.
The actual yield base shear force (yield strength) V
y
of a system that is designed for
a design base shear force of V
d
is usually larger than V
d
(i. e. I

> I
d
) because of the
overstrength inherent in design. The overstrength reduction factor R
ov
describes this
deviation from the target strength. Various factors contributing to overstrength are;
material strength reduction factors (
cd
=
]
ck
y
c
foi conciete, etc. ) ,
minimum dimensions,
B. Sucuolu 8

minimum reinforcement ratio in RC members,
minimum strength of materials,
detailing requirements,
redundancy (redistribution of internal forces from the yielded to non-yielded
members in indeterminate systems).

We can simply combine R

and R
ov
in Eqs. (5.4) and (5.5) into a single reduction factor.

R

x R
o
=
v
c
v
j
.
v
j
v
d
=
v
c
v
d
= R
u
(5.6)
R
a
(T) is called the earthquake force reduction factor. In the 2007 Turkish Earthquake
Code, R
a
(T) is defined by a bi-linear spectral curve shown in Fig. 5.8.
Accordingly, the reduced design spectrum S
aR
is defined by

S
uR
(I) =
S
cc
(1)
R
c
(1)
(5.7)
which is similar to Eq. (5.3).










Fig. 5.8. Earthquake force reduction factor in the Turkish Earthquake Code (2007).

R
a
(T) in the Turkish Earthquake Code depends on another factor R as shown in
Fig. 5.8, which is called the structural system response factor. When Fig. 5.8 is compared
with Fig. 2.29, we may observe that R represents the ductility capacity for an equivalent
inelastic SDOF system, and T
A
is the corner period of the design earthquake ground
motion. The R factors in the Code include both ductility and overstrength however as
shown in Eq. (5.6).
B. Sucuolu 9

R factors are described in Table 2.5 of the 2007 Turkish Earthquake Code for
various structural systems and for two ductility levels, one with ordinary ductility and the
other for enhanced ductility implemented in design. These ductility levels are imposed by
capacity design requirements discussed in the following Chapter. The R factors in Table
2.5 are based on judgment as well as experimental and analytical verifications.
The reduced design spectra in the Turkish Earthquake Code for R=4 (ordinary RC
frame) and R=8 (ductile RC frame) are shown in Fig. 5.9, together with the linear elastic
design spectrum.










Fig. 5.9. Earthquake design spectra in the Turkish Earthquake Code (2007) for linear elastic (R=1),
ordinary (R=4) and ductile (R=8) RC frames.



5.3 ANALYSIS PROCEDURES

There are two basic linear elastic analysis procedures in seismic design codes which
are carried out under the design earthquake represented by a reduced design spectrum
S
aR
(T). The first one is the modal superposition procedure and the second one is the
equivalent static lateral load procedure, which is derived from the first one as a special case
applicable to simple, regular structures.
In both seismic analysis procedures, only those degrees of freedom which the
inertial forces act are considered in the equations of motion. These are called the dynamic
degrees of freedom. The remaining static degrees of freedom are necessary for calculating
the internal forces under gravity loads. However they can be eliminated from the dynamic
equations of motion by a method called static condensation, which leads to a significantly
reduced number of degrees of freedom compared to the original system.
B. Sucuolu 1u

5.3.1 Reduction of Degrees of Freedom: Static Condensation
When the slabs act as rigid diaphragms in their own plane, then the motion of each
slab during earthquake can be defined by three dynamic degrees of freedom defined at its
centre of mass. On the other hand, almost the entire mass of a building is confined to the
slabs (concrete slab, cover, beams, live loads, hung ceilings, etc). Only columns and
partition walls are not a part of the slab system; however their masses can be distributed
evenly to the adjacent slabs at top and bottom. Accordingly, the inertial forces which act
on the story masses during an earthquake can be defined on the slabs.
Lets consider a rigid slab with mass m moving in its own plane. Two consecutive
positions of the rigid slab are shown in Fig. 5.10.a with the local coordinate axes x-y and
x-y, respectively. The motion of the centre of mass in the plane of motion is sketched in
Fig. 5.10.b. The motion of the corner point A (u
xA
, u
xB
) can be expressed in terms of the
translational motion of the centre of mass (u
x
, u
y
), rotation of the rigid slab 0
z
about its
centre of mass, and the position of A with respect to the centre of mass (x
A
,y
A
).

u
xA
= u
x
- 0
z
y
A
(5.8.a)
u
A
= u

- 0
z
x
A
(5.8.b)













Fig. 5.10. Motion of a rigid slab in its own plane.
B. Sucuolu 11

Hence, the inertial forces acting on the slab can be expressed in terms of two
inertial forces f
x
, f
y
and a torsional moment M
z
.

x
= m u
x
totuI


;

= m u

totuI


;
H
z
= I
z
0

z
totuI


(5.9)

In Eqs. (5.9),
u
x
totuI

= u
x
+u
gx

, u

totuI

= u

+u
g

anu 0

z
totuI
= 0

z


The total and relative rotations are equal since the ground motions do not have rotational
components generally. I
z
= m
(u
2
+ b
2
)
12
for rectangular slabs with dimensions a and b.
u
x
,u
y
and
z
at each floor are considered as the dynamic degrees of freedom (3xN
for an N-story 3D frame) whereas all other DOFs are called the static degrees of freedom
because a mass is not assigned to them (column and beam end rotations, slab edge
rotations, axial deformations). Dynamic forces do not act on static DOFs.
We can eliminate the static degrees of freedom during dynamic analysis by a
procedure called static condensation. Lets define the displacements along dynamic DOFs
by u
d
and those along static DOFs by u
s
. The dynamic and static DOFs of a single story,
multi-bay frame are sketched in Fig. 5.11.












Fig. 5.11. Dynamic and static DOFs of a single story, multi-bay frame.

Accordingly, the vector of inertial forces acting on dynamic DOFs is
d
whereas

s
=0 since no dynamic forces act on the static DOFs. Then the stiffness equation between
forces and displacements under dynamic excitation becomes,
B. Sucuolu 12

_

d
u
_ = _
k
dd
k
ds
k
sd
k
ss
_ _
u
d
u
s
_
(5.10)
The second row of Eq. (5.10) can be expanded as
k
sd
u
d
+ k
ss
u
s
= u (5.11)
which yields
u
s
= -k
ss
-1
k
sd
u
d
(5.12)
Substituting u
s
from Eq. (5.12) into the first row of Eq. (5.10) gives

d
= (k
dd
- k
ds
k
ss
-1
k
sd
) u
d
k
d
u
d
(5.13)
The term in the parenthesis in Eq. (5.13) is called the condensed stiffness matrix k
d
which
has a size of (3Nx3N) in an N-story 3D space frame and a size of N in a 2D plane frame.
Static condensation reduces the size of the matrix equation of motion enormously. The 2D
frame in Fig. 5.11 has a total of 9 DOFs whereas it reduces to a 1 DOF system after static
condensation.

5.3.2 Mode Superposition Procedure

A modal superposition analysis is carried out for the condensed system under the
reduced design earthquake Sa
R
by using a sufficient number of modes. This method is
applicable to all buildings without any restrictions.
Eigenvalue analysis is conducted on the condensed system with stiffness k
d
in Eq.
(5.13) and with a lumped- mass diagonal matrix m defined in Eq. (5.14). The components
of the mass matrix in a 3D building are assigned at each story, which are the story mass in
two translational directions x and y, and the mass moment of inertia in the rotational
direction
z
along the dynamic DOFs of the associated slab.
m
(3Nx3N)
=
l
l
l
l
l
l
l
l
l
m
1
m
1
I
1
m
2

m
2

I
2

.
.
.
1
1
1
1
1
1
1
1
1
(5.14)
B. Sucuolu 1S

Bence, m
i
is the mass of the ith story, and I

= m

u
1
x b
1
2
12
is the mass moment of inertia
of the ith slab in Eq. (5.14).
The equation of motion for the condensed system under x or y direction of ground
motion is obtained from Eq. (3.3).

m u
d
+ k
d
u
d
= -m 1 u
g
i = x oi y (5.15)

When the right hand side is zero during free vibration, we obtain the eigenvalue problem.

m u
d
+ k
d
u
d
= u (5.16)

The solution of eigenvalue problem gives the eigenvalues
n
2
and the eigenvectors

n
of the condensed system. The eigenvector
n
contains two translational components

xn
anu
n
, and one rotational component
zn
at each floor i of a 3D building. The
modal forces
n
also include two horizontal forces and a torque at each floor accordingly.

n
=
`
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1

x1n

1n

z1n
-

x2n

2n

z2n
-
.
.
.
-

xNn

Nn

zNn
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1

n
=
`
1
1
1
1
1
1
1
1
1
1
1
1
1
1

x1n

1n
H
z1n
-

x2n

2n
H
z2n
-
.
.
.
-

xNn

Nn
H
zNn
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1

(5.17)
In a 2D plane frame, the
n
and
zn
components in
n
do not exist.
The modal forces under the reduced design earthquake spectrum follows from Eq.
(3.51).

n
=
L
n
M
n
[m
n
S
uR,n
(5.18)
Then we apply
n
in Eq. (5.17) to the uncondensed building structure and calculate
member forces and displacements at the nth mode from static analysis. Two horizontal
B. Sucuolu 14

force resultants and one torsion moment applied at the centre of mass of the jth floor slab
of a 3D structure is shown in Fig. 5.12.








Fig. 5.12. Dynamic force components at the nth mode, acting at the mass centre of the jth floor
slab.

If the 3D building is symmetrical about the x axis, then
]n
= 0 and H
z]n
= 0
under excitation S
aR,x
in the x direction for all modes.
Finally, we combine the modal results by SRSS or CQC formulation. For example,
the design moment at the top end of the front right corner column in Fig. 5.12 is calculated
from
H

= (H
1
)
2
+(H
2
)
2
++ (H
N
)
2

(5.19)

Minimum Number of Modes
The total effective mass of the N
min
modes considered in the mode superposition
analysis should be larger than 90% of the total mass, separately in the x and y directions.
This requirement is verified from the following inequalities.
x Jircction: H
n
-
N
min
n=1
=
I
xn
2
H
n
N
min
n=1
u.9u m

N
=1

(5.20)
y Jircction: H
n
-
N
min
1
=
I
n
2
H
n
N
min
n=1
u.9um

N
1

(5.21)

In Eqs. (5.20) and (5.21), N is the number of stories and m
i
is the story mass. Also,
B. Sucuolu 1S

I
xn
= m

xn
N
=1
; I
n
= m

n
N
=1

(5.22)
and,
H
n
= (m

xn
2
N
1
+ m

n
2
+ I
z
.
zn
2
)
n
1
m
n
. (5.23)

It should be noticed that Eqs. (5.22) and (5.23) are the expanded scalar forms of Eqs.
(3.33) and (3.30) respectively, where

I
xn
=
n
1
m l
x
; I
n
=
n
1
m l

; H
n
=
n
1
m
n
(5.24)

and l
x
= {1 u u ; 1 u u ; ]
1
; l

= {u 1 u ; u 1 u ; ]
1
are the
influence vectors in the x and y directions, respectively. l
x
and l

transmit the motion of

the ground in the x and y directions to the respective translational dynamic DOFs of the
structure above as rigid body motion components.

Summary
The mode superposition analysis procedure in the Code can be summarized with the
following steps.
1. Prepare a complete structural model of your structure.
2. Condense the static DOFs (Eq. 5.13).
3. Carry out eigenvalue analysis of the condensed structure (Eq. 5.16) and determine

n
(or T
n
) and
n
for each mode n.
4. Calculate modal spectral accelerations from the design spectrum S
aR,n
(Eq. 5.7) for
a proper R factor.
5. Calculate the modal forces
n
=
L
n
M
n
[m
n
S
uR,n
(Eq. 5.18).
6. Apply
n
to the complete (uncondensed) structural model by expanding
n
to the
complete force vector '
n
as shown in Fig. 5.12, and determine internal modal
member forces and deformations r
n
from '
n

= k u
n
where k is the full
(uncondensed) stiffness matrix and u
n
includes all DOFs.
7. Combine the modal results by SRSS: r
L

= (r
1
)
2
++(r
n
)
2
++ (r
N
)
2
.
8. Further combine gravity and earthquake analysis results: r
dcsgn
= r
gut
+r
L


B. Sucuolu 16

Example 5.1. A two story, one bay frame with six DOFs is given in Fig. (a). All frame
members have a length of L, moment of inertia of I and the modulus of elasticity is E. A
uniform distributed vertical gravity load with intensity q is acting on the beams. Determine
the design moments and shear forces in the column AC and the beam CD under gravity and
earthquake loads. Design earthquake is defined with the reduced design spectrum in the
Turkish Earthquake Code 2007 for seismic zone 1, soil type Z3 and an ordinary ductility
level, which is given in Fig. (b).









(a) Frame structure (b) Reduced design spectrum

Solution
The procedure summarized above will be implemented in the solution.

Static Condensation
The 6 DOF system in Fig. (a) will be reduced to a 2 DOF dynamic system for eigenvalue
and mode superposition analyses. Displacement vector u of the unreduced 6 DOF system
and the displacement vector u
d
of the reduced (condensed) 2 DOF system are given below.
Hence, the condensed system DOFs are the lateral DOFs along the floor levels where the
story masses are defined and accordingly the inertial forces develop.

u =
`
1
1
1
1
u
1
u
2
u
3
u
4
u
5
u
6

1
1
1
1
1
u
d
= _
u
1
u
2

_ (1)

The stiffness matrix of the 6 DOF system is

k
ss
=
LI
L
3

l
l
l
l
l
l
48 -24 u
-24 24 6I
u 6I 12I
2
u
6I
2I
2
-6I -6I
6I 6I
2I
2
u
u 6I 2I
2
12I
2
u 2I
2
-6I
-6I
6I
6I
2I
2
u
u
2I
2
8I
2
2I
2
2I
2
8I
2
1
1
1
1
1
1
(2)


L
L
L
E
A
F
B
C B
u
4
u
1
u
2
u
6
u
S
u
S
EI
m
m
B. Sucuolu 17


The stiffness matrix above can be partitioned as

k
ss
= _
k
dd
k
ds
k
sd
k
ss
_

where the condensed stiffness matrix k
d
is expressed as k
d
= k
dd
k
sd
T
k
ss
-1
k
ds
. Then,
k
d
=
EI
17I
3
_
69u -Suu
-Suu 228
_
Similarly, the mass matrix for the condensed 2 DOF system is
m = _
m m
m m
_

Eigenvalue Analysis
The equation det (k
d

2
m ) =0 should be solved for determining the eigenvalues and
eigenvectors. Here, we will assign numerical values to frame properties.

Let EI =660 kN.m
2
, L =2 m and m =10 tons. Then, the eigenvalues are obtained as:

1
2
=39.00 (rad/s)
2
;
2
2
=406.50 (rad/s)
2
and T
1
=1.00 s ; T
2
=0.31 s.

The mode shapes are determined by solving the the equation (k
d
-
2
m)
n
= u . The
solution gives;

1
= _
u.49
1.uu
_ onJ
2
= _
-2.uS
1.uu
_ (3)

Spectral Accelerations
Spectral acceleration values for the modal periods are obtained from the reduced design
spectrum of TEC 2007 given in Fig. (b) above (R=4, Zone 1, soil type Z3):

Mode 1: T
1
=1.00 s, S
aR,1
=1.63 m/s
2
Mode 2: T
2
=0.31 s, S
aR,2
=2.45 m/s
2


Modal Force Vectors

n
=
L
n
M
n
[m
n
S
uR,n
where I
n
=
n
1
m l

; H
n
=
n
1
m
n
and l

= ]
1
1

When the respective values of
n
, m anu l

are substituted into these expressions, we
find
L
1
=14.92 tons ; L
2
=-10.32 tons; M
1
=12.42 tons ; M
2
=51.29 tons, and

1
= _
9.6S
19.S8
_ kN ;
2
= _
1u.uS
-4.9S
_ kN (4)
B. Sucuolu 18

Earthquake Analysis (Mode Superposition Procedure)
The modal force vectors of the condensed 2 DOF system are first expressed for the
uncondensed (original) 6 DOF system in view of the DOFs defined in Fig. (a).

'
1
=
`
1
1
1
1
9.6S
19.S8
u
u
u
u
1
1
1
1
1
kN ; '
2
=
`
1
1
1
1
1u.uS
-4.9S
u
u
u
u
1
1
1
1
1
kN (5)

Then the modal displacement vectors are obtained by solving '
n

= k
ss
u
n
where k
sys

is the 6X6 global system stiffness matrix in Eq. (2). Solution for n =1 and n =2 gives,

u
1
=
`
1
1
1
1
u.u247
u.uSu2
-u.uu99
-u.uu99
-u.uuS7
-u.uuS7
1
1
1
1
1
; u
2
=
`
1
1
1
1
u.uu2S
-u.uu12
u.uuu1
u.uuu1
u.uu11
u.uu11
1
1
1
1
1
(6)
The units are meters and radians.

Earthquake Forces in Member AC
Member forces are calculated from the member equilibrium equation;


AC,n

= k
AC
u
AC,n


k
AC
=
EI
I
3
_
12 -6I -12 -6I
-6I 4I
2
6I 2I
2
-12
-6I
6I
2I
2
12 6I
6I 4I
2
_ ; u
AC
= _
u
A
0
A
u
C
0
C
_ = _
u
u
u
1
u
3
_

Mode 1

AC,1
= _
I
A
H
A
I
C
H
C
_ = k
AC
_
u
u
u
1
u
3
_ = k
AC
_
u
u
u.u247
-u.uu99
_ = _
-14.61
17.89
14.61
11.S2
_ kN and kN.m

Mode 2

AC,2
= _
I
A
H
A
I
C
H
C
_ = k
AC
_
u
u
u
1
u
3
_ = k
AC
_
u
u
u.uu2S
u.uuu1
_ = _
-2.SS
2.S1
2.SS
2.S8
_ kN and kN.m


u
A
=u

A
=u

C
=u
S
u
C
=u
1
A
C
B. Sucuolu 19

Earthquake Moment Diagram AC









Mode 1 Mode 2 SRSS

M
AC,bot
=(17.89
2
+2.51
2
)
1/2
= 18.06 kN.m; M
AC,top
=(11.32+2.58
2
)
1/2
= 11.61 kN.m

Earthquake Forces in Member CD
Member forces are calculated from the member equilibrium equation;


C,n

= k
C
u
C,n


k
C
=
EI
I
3
_
12 6I -12 6I
6I 4I
2
-6I 2I
2
-12
6I
-6I
2I
2
12 -6I
-6I 4I
2
_ ; u
C
= _
u
C
0
C
u

_ = _
u
u
3
u
u
4
_




Mode 1

C,1
= _
I
C
H
C
I

_ = k
C
_
u
u
3
u
u
4
_ = k
C
_
u
-u.uu99
u
-u.uu99
_ = _
-19.7u
-19.7u
19.7u
-19.7u
_ kN and kN.m

Mode 2

C,2
= _
I
A
H
A
I
C
H
C
_ = k
C
_
u
u
u
1
u
3
_ = k
C
_
u
u.uuu1
u
u.uuu1
_ = _
u.21
u.21
-u.21
u.21
_ kN and kN.m

17.89kN.m
11.32kN.m
2.51kN.m
2.58kN.m
18.06kN.m
11.61kN.m
B
C
uC=u
uB=u
C=uS B=u4
B. Sucuolu 2u

Earthquake Moment Diagram CD





Mode 1 Mode 2






SRSS

M
CD,l
=(19.70
2
+0.21
2
)
1/2
= 19.71 kN.m ; M
CD,r
=(19.70
2
+0.21
2
)
1/2
= 19.71 kN.m


Gravity Load Analysis

Let q=50 kN/m. This value is consistent with the story mass of 10 tons, hence 10g kN is
distributed uniformly over the story girders of L=2 m. Fixed-end moments at beam ends
are calculated from M
FEM
=qL
2
/12 =16.67 kN.m.

Accordingly, the gravity force vector is

u
=
`
1
1
1
1
u
u
-16.67
16.67
-16.67
16.67
1
1
1
1
1
kN. m

Displacement vector under gravity forces is determined by solving
u

= k
ss
u
u
. The
global displacement vector and the member end displacements are obtained as,

u
u
=
`
1
1
1
1
u
u
-u.uuS6
u.uuS6
-u.uu72
u.uu72
1
1
1
1
1
; u
AC
= _
u
A
0
A
u
C
0
C
_ _
u
u
u
1
u
3
_ = _
u
u
u
-u.uuS6
_; u
C
= _
u
C
0
C
u

_ = _
u
u
3
u
u
4
_ = _
u
-u.uuS6

u
u.uuS6
_

Then the member end forces under gravity loads are determined from

19.70kN.m
19.70kN.m
0.21kN.m
0.21kN.m

19.70kN.m
19.70kN.m
q
L= 2 m.

R

C
D
B. Sucuolu 21


AC,u

= k
AC
u
AC
+F
cxt
and
C,u

= k
C
u
C
+F
cxt


where F
cxt,AC
= u (no span loauing) anu F
cxt,C
= _
u
16.67
u
-16.67
_ kN. m. Then,

AC,u
= _
S.S7
-2.S8
-S.S7
-4.76

_ anu
C,u
= _
u
14.Su
u
-14.Su

_


Gravity Moment Diagrams of AC and CD







AC CD







Combining the Internal Forces: M
G
+ M
EQ



Member AC: M
G
+M
EQ

















-2.38 kN.m
4.76 kN.m
-14.30 kN.m
-14.30 kN.m
+
=
-6.85kN.m
15.68 kN.m 18.06 kN.m
-11.61 kN.m
-2.38 kN.m
4.76 kN.m
B. Sucuolu 22

Member AC: M
G
- M
EQ
















Member CD: M
G
+M
EQ















Member CD: M
G
- M
EQ













-2.38 kN.m
4.76 kN.m
18.06 kN.m
-11.61 kN.m
-
=
19.70 kN.m
-19.70 kN.m
+
=
5.4 kN.m
-34 kN.m
-14.30 kN.m
-14.30 kN.m
19.70 kN.m
-19.70 kN.m
-14.30 kN.m
-14.30 kN.m
-
=
5.4 kN.m
-34 kN.m
16.37 kN.m
-20.44 kN.m
B. Sucuolu 2S

5.3.3 Equivalent Static Lateral Load Procedure

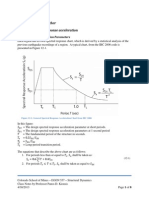
Lets consider the effective modal forces and the resulting modal displacements at
the nth mode of a building in Fig. 5.13, as discussed in Section 3.4.2.













Fig. 5.13. Modal forces and resulting modal displacements at the nth mode of a building.


The modal force vector
n
under the reduced design spectrum S
uR
was given in Eq. (5.18).
Then the base shear force at the nth mode can be obtained from Eq. (3.53).

I
bn
= H
n
-
S
uR,n

I
n
2
H
n
S
uR,n

(5.25)

The jth component of
n
in Eq. (5.18) and Fig. 5.13 can be expressed in scalar form as

]n
=
I
n
H
n
(m
]

]n
) S
uR,n

(5.26)

When we multiply and divide the RHS by I
n
and rearrange;

]n
=
I
n
2
H
n
.
1
I
n
(m
]

]n
) S
uR,n

(5.27)

Substituting I
bn
from Eq. (5.25) into Eq. (5.27), we obtain

]n
= I
bn
m
]

]n
I
n

(5.28)
where
B. Sucuolu 24

I
n
=
n
1
m 1 m

n
N
=1

(5.29)

Note that I
n
in Eq. (5.29) is identical to its definitions in Eq. (5.22) in the x and y
directions, respectively. Finally, substituting I
n
from Eq. (5.29) into Eq. (5.28), we get

]n
= I
bn
m
]

]n
m

n
N
i=1

(5.30)

Multiplying and dividing the RHS by the gravitational acceleration g gives,

]n
= I
bn
w
]

]n
w

n
N
i=1

(5.31)

where w

= m

g is the weight of the ith floor.

If the first mode (in the direction of earthquake excitation) is dominant on total
dynamic response, then
I
b
I
b1
H
1
-
S
uR,1
(5.32)
from Eq. (5.25). Similarly, from Eq. (5.31), considering that I
b
I
b1
,

]

]1
= I
b
w
]

]1
w

1
N
i=1

(5.33)

The components of the first mode vector
1
in the direction of earthquake
excitation can be approximated with a linear variation over the building height in simple
buildings with regular height wise distribution of mass and stiffness.

]1
= o E
]
(5.34)
H
j
is the height of the jth floor from the base and o is an arbitrary constant representing
the slope of linear distribution. Substituting
]1
from Eq. (5.34) into Eq. (5.33), we obtain

]
= I
b
w
]
E
]
w

N
=1

(5.35)


B. Sucuolu 2S

Base Shear Force in the Code

It was proposed in Eq. (5.32) that I
b
H
1
-
S
uR,1
in simple regular buildings where
H
1
-
=
L
1
2
M
1
is the effective modal mass of the first mode. If we replace H
1
-
with the total
mass H
-
= m

, then we approximately account for the masses of higher modes. Hence,

I
b
= H. S
uR,1

w
g
S
uc
(I
1
)
R
u
(I
1
)

(5.36)
where w = w

N
=1
; w
i
= g
i
+ nq
i
; g
i
is the dead load, q
i
is the live load and n is the live
load reduction factor for dynamic mass.
Live load is reduced by the n factor in calculating the lateral earthquake forces
which are based on the weight (mass) of the building during the earthquake. It is
considered that the entire live load assumed in gravity design (factored dead load and live
load combination) has a small probability of existence during an earthquake. Accordingly
the mass of the live load is reduced by n <1 to prevent overdesign. This factor mostly
depends on how long the live load mass can be permanent in a building. It is 0.3 for
residences and offices, 0.6 for schools, dormitories, concert halls, restaurants and shops.

Lateral Force Distribution in the Code

The distribution of lateral forces to the stories, given in Eq. (5.35), is slightly
modified in the Code and expressed by Eq. (5.37).

]
= (I
b
- F
n
)
o
]
H
]
w
i
H
i
N
i=1
; F
N
= u.uu7S N I
b
(5.37)
F
N
is the portion of lateral force applied to the roof in order to produce higher mode
response. This is not an effective way of including higher mode response however. It only
leads to larger overturning moments at the base.
The lateral force distribution in the Code for the Equivalent Static Lateral Load
Procedure is shown in Fig. 5.14.



B. Sucuolu 26
















Fig. 5.14. Earthquake force distribution in the Code for equivalent static lateral load procedure.

Estimation of the First Mode Period T
1

The first mode period T
1
is required in calculating the reduced base shear force
from Eq. (5.36). T
1
can be calculated by an approximate procedure, called Rayleighs
method. Let F
fi
be a lateral force distributions and d
fi
be the resulting lateral story
displacements, obtained by static analysis. Then
I
1
= 2n _
m
i
d
]i
2 N
i=1
P
]i
d
]i
N
i=1
_
12
(5.38)
F
fi
can have any distribution, however using
]
in Eq. (5.35) for F
fi
increases accuracy.

Limitations of the Equivalent Static Lateral Load Procedure
Equivalent static lateral force procedure is only applicable to regular buildings
where the first mode in the earthquake direction is dominant on earthquake response. The
limitations are;
H
N
25 m and
b
2.0
in seismic zones 1 and 2, where H
N
is the total building height from the base, and

b
=

i,mcx

i,ccrcgc
(5.39)
is the torsional irregularity coefficient defined in Fig. 5.15 for the ith story floor slab.
B. Sucuolu 27













Fig. 5.15. Definition of the terms in torsional irregularity coefficient.


5.3.4 Accidental Torsion

The centre of rigidity of the original structure at any floor may be shifted because
of several reasons, and accordingly creates an additional eccentricity which is not
accounted for in the structural modeling of the system. This phenomenon is called
accidental torsion in seismic design. The probable causes of accidental torsion are;
Non-synchronized cracking or yielding of lateral load resisting vertical members
(columns and shear walls) in a story, leading to unsymmetrical stiffness loss during
a strong earthquake excitation.
Unsymmetrical distribution of non-structural members which carry a part of the
story shear forces (partition walls, window frames, etc.).
Shift in the centre of rigidity due to imperfections in construction.
Shift in the centre of mass due to a concentrated live load mass.

Seismic design codes account for accidental torsion indirectly, by imposing an additional
eccentricity to the applied inertial lateral force resultants. This is achieved by shifting the
centre of mass at each story in the direction perpendicular to the earthquake direction by an
additional eccentricity equal to 5% of the floor dimension in the transverse direction. The
shift is imposed in the x and y directions separately, and in both (+/-) senses. The shift at
the ith floor in the x direction is shown in Fig. 5.16.

B. Sucuolu 28










Fig. 5.16. Shifting the centre of mass to account for accidental torsion.



REFERENCES

Turkish Earthquake Design Code for Buildings, Ministry of Reconstruction, Ankara, 2007.