Calculs de (2) =

n=1
1
n
2
1) 1er calcul de
+

n=1
1
n
2
. De nombreux dveloppements en srie de Fourier fournissent la valeur de
+

n=1
1
n
2
. En voici
un exemple.
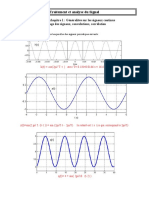
a) Soit f la fonction dnie sur R valeurs dans R, 2-priodique telle que x [, ], f(x) = |x|.
1 2 3 4 5 6 1 2 3 4 5 6
1
2
3
y
=
f
(
x
)
f est 2-priodique, continue sur R, de classe C
1
par morceaux et donc, daprs le thorme de Dirichlet, en tout rel
x, la srie de Fourier de f converge vers f(x).
b) Calcul des coecients de Fourier de f.
f est paire et donc n 1, b
n
(f) = 0 puis, pour n N, a
n
(f) =
2

0
t cos(nt) dt.
a
0
(f) =
2

0
t dt = .
Pour n N

, une intgration par parties fournit

a
n
(f) =
2

0
t cos(nt) dt =
2

__
t
sin(nt)
n
_

1
n

0
sin(nt) dt
_
=
2
n

0
sin(nt) dt
=
2
n
_
cos(nt)
n
_

0
=
2((1)
n
1)
n
2

.
c) Puisque f est somme de sa srie de Fourier sur R, on obtient pour tout rel x
f(x) =
a
0
(f)
2
+
+

n=1
(a
n
(f) cos(nx) + b
n
(f) sin(nx)) =

2
+
+

n=1
2((1)
n
1)
n
2

cos(nx) =

2

4

p=0
cos((2p + 1)x)
(2p + 1)
2
.
En particulier
x [, ], |x| =

2

4

p=0
cos((2p + 1)x)
(2p + 1)
2
.
x = 0 fournit alors

2

4

p=0
1
(2p + 1)
2
= 0 et donc
+

p=0
1
(2p + 1)
2
=

2
8
. Enn
S =
+

n=1
1
n
2
=
+

p=1
1
(2p)
2
+
+

p=0
1
(2p + 1)
2
=
1
4
S +

2
8
et donc S =
4
3


2
8
=

2
6
.
+

n=1
1
n
2
=

2
6
et
+

n=0
1
(2n + 1)
2
=

2
8
.
http ://www.maths-france.fr 1 c Jean-Louis Rouget, 2008. Tous droits rservs.
2) 2eme calcul de
+

n=1
1
n
2
(version maths sup). Le travail prcdent peut tre eectu la main en maths sup.
On tablit dabord un outil capital de la dmonstration du thorme de Dirtichlet : le lemme de Lebesgue.
a/ Une expression de
1
n
2
sous forme intgrale.
On cherche des rels a et b tels que n 1,

0
(at
2
+ bt) cos(nt) dt =
1
n
2
.
Soit n N

. Deux intgrations par parties fournissent

0
(at
2
+ bt) cos(nt) dt =
_
(at
2
+ bt)
sin(nt)
n
_

1
n

0
(2at + b) sin(nt) dt =
1
n

0
(2at + b)(sin(nt)) dt
=
1
n
__
(2at + b)
cos(nt)
n
_

0
(2a)
cos(nt)
n
dt
_
=
1
n
2
((2a + b)(1)
n
b)
2a
n
2

0
cos(nt) dt =
((1)
n
(2a + b) b)
n
2
.
Maintenant, si les rels a et b vrient 2a + b = 0 et b = 1 ou encore si b = 1 et a =
1
2
, alors
n 1,

0
(at
2
+ bt) cos(nt) dt =
1
n
2
. Donc
n N

,
1
n
2
=

0
_
t
2
2
t
_
cos(nt) dt.
b) Expression de
n

k=1
1
k
2
sous forme intgrale.
i) Pour n N

, posons S
n
=
n

k=1
1
k
2
. Daprs a),
S
n
=
n

k=1

0
_
t
2
2
t
_
cos(kt) dt =

0
_
t
2
2
t
_
n

k=1
cos(kt) dt.
ii) Calcul de
n

k=1
cos(kt).
1er calcul. Soit t un rel et n un entier naturel non nul.
n

k=1
cos(kt) =
n

k=1
Re(e
ikt
) = Re
_
n

k=1
e
ikt
_
= Re
_
n

k=1
(e
it
)
k
_
.
Si t 2Z alors chaque cos(kt) vaut 1 et dans ce cas,
n

k=1
cos(kt) = n.
Si t / 2Z, alors e
it
= 1 et dans ce cas
n

k=1
cos(kt) = Re
_
n

k=1
(e
it
)
k
_
= Re
_
e
it
1 e
int
1 e
it
_
= Re
_
e
i(1+
n
2

1
2
)t
e
int/2
e
int/2
e
it/2
e
it/2
_
= Re
_
e
i(n+1)t/2
sin(nt/2)
sin(t/2)
_
=
sin
_
nt
2
_
cos
_
(n + 1)t
2
_
sin
_
t
2
_ =
sin
_
(2n + 1)t
2
_
sin
_
t
2
_
2 sin
_
t
2
_
=
1
2
+
sin
_
(2n + 1)t
2
_
2 sin
_
t
2
_ .
http ://www.maths-france.fr 2 c Jean-Louis Rouget, 2008. Tous droits rservs.
Finalement,
n N

, t R,
n

k=1
cos(kt) =
1
2
+
n
(t) o
n
(t) =

n +
1
2
si t 2Z
sin
_
(2n + 1)t
2
_
2 sin
_
t
2
_ si t / 2Z
.
2me calcul. Soient t un rel et n un entier naturel non nul.
2 sin
_
t
2
_
n

k=1
cos(kt) =
n

k=1
sin
_
k +
1
2
)t
_
sin
_
k
1
2
)t
_
= sin
_
(n +
1
2
)t
_
sin
_
t
2
_
(somme tlescopique).
et pour t / 2Z, on retrouve
n

k=1
cos(kt) =
1
2
+
sin
_
(2n + 1)t
2
_
2 sin
_
t
2
_ .
iii) Daprs ce qui prcde,
n
est continue sur [0, ] (car pour tout t de [0, ],
n
(t) =
n

k=1
cos(kt)) et pour n N

k=1
1
k
2
=

0
_
t
2
2
t
__

1
2
+
n
(t)
_
dt =
1
2
_
t
3
6

t
2
2
_

0
+

0
_
t
2
2
t
_

n
(t) dt
=

2
6
+

0
_
t
2
2
t
_

n
(t) dt.
Maintenant, pour t ]0, ],
_
t
2
2
t
_

n
(t) =
t
2
2
t
2 sin
_
t
2
_ sin
_
(2n + 1)t
2
_
. Pour t ]0, ], on pose alors f(t) =
t
2
2
t
2 sin
_
t
2
_.
f est continue sur ]0, ]. De plus, quand t tend vers 0, f(t)
t
2
t
2
= 1. f se prolonge donc par continuit en 0 en
posant f(0) = 1.
En rsum,
n N

,
n

k=1
1
k
2
=

2
6
+

0
f(t) sin
_
(2n + 1)t
2
_
dt o f(t) =

t
2
2
t
2 sin
_
t
2
_ si t ]0, ]
1 si t = 0
.
Il reste tudier la limite quand n tend vers + de lexpression prcdente, f tant continue sur [0, ].
c) Le lemme de Lebesgue. Il sagit de montrer que pour toute fonction f continue par morceaux sur un segment [a, b]
valeurs dans R ou C, lim
+

b
a
f(t)e
it
dt = 0 et donc aussi lim
+

b
a
f(t) cos(t) dt = lim
+

b
a
f(t) sin(t) dt = 0.
i) Cas des fonctions de classe C
1
.
Soit f une fonction de classe C
1
sur un segment [a, b] valeurs dans R ou C. Une intgration par parties, licite puisque
f est de classe C
1
sur [a, b] fournit pour > 0
http ://www.maths-france.fr 3 c Jean-Louis Rouget, 2008. Tous droits rservs.

b
a
f(t)e
it
dt =
1
i
_
_
f(t)e
it

b
a

b
a
f

(t)e
it
dt
_
=
1
i
_
f(b)e
ib
f(a)e
ia

b
a
f

(t)e
it
dt
_
,
et donc, pour > 0

b
a
f(t)e
it
dt

_
|f(b)| + |f(a)| +

b
a
|f

(t)| dt
_
.
Cette dernire expression tend vers 0 quand tend vers +ce qui dmontre le lemme de Lebesgue pour les fonctions
de classe C
1
sur un segment.
ii) Cas des fonctions continues par morceaux.
On a dabord lim
+

b
a
e
it
dt = lim
+
e
ib
e
ia
i
= 0 ce qui dmontre le lemme de Lebesgue quand f est
la fonction constante 1.
Mais alors, par linarit de lintgrale puis additivit par rapport lintervalle dintgration, le lemme de Lebesgue
est dmontr pour les fonctions en escaliers sur [a, b].
Soit maintenant f une fonction continue par morceaux sur [a, b] valeurs dans R ou C.
Soit > 0. On sait quil existe g une fonction en escaliers sur [a, b] telle que t [a, b], |f(t) g(t)|

2(b a)
(approximation uniforme sur un segment dune fonction continue par morceaux par une fonction en escaliers).
Pour > 0, on a alors

b
a
f(t)e
it
dt

b
a
(f(t) g(t))e
it
dt +

b
a
g(t)e
it
dt

b
a
|f(t) g(t)| dt +

b
a
g(t)e
it
dt

b
a

2(b a)
dt +

b
a
g(t)e
it
dt

=

2
+

b
a
g(t)e
it
dt

.
Maintenant, puisque g est en escaliers sur [a, b], il existe > 0 tel que, pour ,

b
a
g(t)e
it
dt

<

2
et
donc

b
a
f(t)e
it
dt

<

2
+

2
= .
On a montr que > 0, > 0/ R, (

b
a
f(t)e
it
dt

< ) et donc
Lemme de Lebesgue pour les fonctions continues par morceaux sur un segment.
Soit f une fonction continue par morceaux sur un segment [a, b] valeurs dans R ou C. Alors
lim
+

b
a
f(t)e
it
dt = 0, lim
+

b
a
f(t) cos(t) dt = 0, lim
+

b
a
f(t) sin(t) dt = 0,
les deux dernires limites tant obtenues par passage aux parties relles et imaginaires.
d) Calcul de
+

n=1
1
n
2
.
La fonction f dnie en b) est continue sur [0, ] et daprs le lemme de Lebesgue, lim
n+

0
f(t) sin
_
(2n + 1)t
2
_
dt = 0.
Le b) montre alors que
+

n=1
1
n
2
=

2
6
.
e) Calcul de
+

n=1
(1)
n1
n
2
et
+

n=0
1
(2n + 1)
2
.
Posons S =
+

n=1
1
n
2
et S

=
+

n=1
(1)
n1
n
2
. On a S S

=
+

n=1
1 (1)
n1
n
2
=
+

p=1
2
(2p)
2
=
1
2
+

p=1
1
p
2
=
1
2
S et donc
http ://www.maths-france.fr 4 c Jean-Louis Rouget, 2008. Tous droits rservs.
S

=
1
2
S =

2
12
. On a aussi S + S

=
+

n=1
1 + (1)
n1
n
2
= 2
+

p=0
1
(2p + 1)
2
et donc
+

p=0
1
(2p + 1)
2
=
1
2
(S + S

) =
3
4
S =

2
8
.
+

n=1
(1)
n1
n
2
=

2
12
et
+

p=0
1
(2p + 1)
2
=

2
8
.
3) 3me calcul de
+

n=1
1
n
2
.
Pour n N

, on pose S
n
=
k
2

k=1
.
a) Calcul de
n

k=1
cotan
2
k
2n + 1
et de
n

k=1
1
sin
2
k
2n + 1
. Pour rel et n entier naturel non nul donns, on a
cos((2n + 1)) + i sin((2n + 1)) = (cos + i sin)
2n+1
=
n

k=0
i
k
C
k
2n+1
cos
2n+1k
sin
k
.
puis par identication des parties imaginaires
sin((2n + 1) =
n

k=0
(1)
k
C
2k+1
2n+1
cos
(2n+1)(2k+1)
sin
2k+1
,
et enn en divisant les deux membres par sin
2n+1
pour / Z, on obtient
sin((2n + 1))
sin
2n+1

=
n

k=0
(1)
k
C
2k+1
2n+1
cos
2n2k

sin
2n2k

=
n

k=0
(1)
k
C
2k+1
2n+1
(cotan
2
)
nk
.
n N, R \ Z,
sin((2n + 1))
sin
2n+1

=
n

k=0
(1)
k
C
2k+1
2n+1
(cotan
2
)
nk
.
Posons alors P =
n

k=0
(1)
k
C
2k+1
2n+1
X
nk
. Posons aussi, pour k 1, n, x
k
= cotan
2
k
2n + 1
.
Tout dabord, pour 1 k n, on a 0 <
k
2n + 1

n
2n + 1
<
n
2n
=

2
. Ainsi les nombres
k
2n + 1
, 1 k n, sont deux
deux distincts et dans ]0,

2
[. Par injectivit de la fonction x cotanx sur ]0,

2
[, les n nombres cotan
k
2n + 1
, 1 k n,
sont deux deux distincts et de plus strictement positifs. Finalement, les n rels x
k
sont deux deux distincts.
Maintenant, pour k 1, n, P(x
k
) =
sin(k)
sin
2n+1
k
2n + 1
= 0. On a donc trouv n rels deux deux distincts racines du
polynme P qui est de degr n. Les relations entre coecients et racines dun polynme permettent darmer que
n

k=1
x
k
=
C
3
2n+1
C
1
2n+1
=
(2n + 1)(2n)(2n 1)/6
2n + 1
=
n(2n 1)
3
.
Donc
n N

,
n

k=1
cotan
2
k
2n + 1
=
n(2n 1)
3
.
Ensuite, pour x / Z,
1
sin
2
x
= 1 + cotan
2
x et donc
n

k=1
1
sin
2
k
2n + 1
=
n

k=1
(1 + cotan
2
k
2n + 1
) = n +
n(2n 1)
3
=
2n(n + 1)
3
.
http ://www.maths-france.fr 5 c Jean-Louis Rouget, 2008. Tous droits rservs.
n N

,
n

k=1
1
sin
2
k
2n + 1
=
2n(n + 1)
3
.
b) Pour x dans ]0,

2
[, on a sin x < x < tan x.
Les fonctions sin et tan sont respectivement strictement concaves et strictement convexes sur ]0,

2
[. On en dduit que les
graphes de ces fonctions sont respectivement strictement au-dessous et strictement au-dessus de leur tangente en (0, 0) sur
]0,

2
[ et donc
x ]0,

2
[, sin x < x < tan x.
Puisque, pour x ]0,

2
[, 0 < sinx < x < tanx, on a aussi aprs passage linverse et lvation au carr
x ]0,

2
[, cotan
2
x <
1
x
2
<
1
sin
2
x
.
c) Encadrement de
n

k=1
1
k
2
. Pour k 1, n,
k
2n + 1
est dans ]0,

2
[ et daprs b), cotan
2
k
2n + 1
<
(2n + 1)
2
k
2

2
<
1
sin
2
k
2n + 1
. En sommant ces ingalits, on obtient daprs a)
n(2n 1)
3
=
n

k=1
cotan
2
k
2n + 1
<
(2n + 1)
2

2
n

k=1
1
k
2
<
n

k=1
1
sin
2
k
2n + 1
=
2n(n + 1)
3
,
ou encore
n N

,
n(2n 1)
3(2n + 1)
2

2
<
n

k=1
1
k
2
<
2n(n + 1)
3(2n + 1)
2

2
.
d) Calcul de (2). Les membres de gauche et de droite de lencadrement prcdent tendent tous deux vers

2
6
quand n
tend vers + et on retrouve donc (2) =

2
6
.
http ://www.maths-france.fr 6 c Jean-Louis Rouget, 2008. Tous droits rservs.