Professional Documents
Culture Documents
Newton Raphson VB A
Uploaded by
rndompersonOriginal Description:
Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Newton Raphson VB A
Uploaded by
rndompersonCopyright:
Available Formats
How To Code the Newton-Raphson Method in Excel VBA
Newtons Algorithm
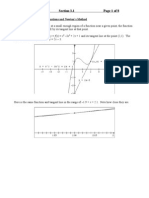
Newton's algorithm, alternately called the Newton-Raphson method, is a numerical method for solving equations of the type f(x)=0. It has numerous applications in finance, and we will use it to determine the volatility surface for a call option using the Black Scholes VBA function. The method applies when we have a close approximation for a solution to the equation. The method assumes that the tangent to the graph at our approximation intersects the x-axis closer to the solution of the equation, i.e. closer to where the line we are evaluating intersects the x-axis. By solving for where the tangent intersects the xaxis, and repeating the process from that point, we get closer and closer to the actual solution of the equation. Let's say we're at our approximate solution, x0. The value of y-axis at this point is y = f(x0). We know that the tangent has gradient f'(x) - the same gradient as the line, from the definition of a tangent. We also know that a univariate linear function takes the form f(x) = mx + c, where m is the gradient, x is the horizontal displacement from the starting point, and c is the vertical displacement from the starting point. As such, we have y = f'(x0)(x-x0) + f(x0) as the line of the tangent. We solve this for y = 0 in order to get the next guesstimate of the solution to f(x) = 0. The above is the simpler method of interpretation, but the statement f(x) = mx+c is actually derived from the more generalised Taylor's series expansion where a continuous, differentiable function f may be expanded about a point c as follows: f(x) =f(c)+f'(c)(x-c)+f''(c)/2!*(xc)^2+... This is the univariate version of the Taylor expansion, but it will suffice for finding, for example, volatility smiles since we assume that all other variables remain constant. Since the equation is linear, no second order derivatives exist so these fall away, leaving f(x) =f(c)+f'(c)(x-c). In our example, x0=c, giving y = f'(x0)(x-x0) + f(x0) The equation of the intersection of the tangent with the y-axis is given by the following: 0 = f'(x0)(x1-x0) + f(x0) We then solve for x1 x1 = x0 - (f(x0)/f'(x0) From this we can induce (though actual proof is out of scope here), that xn+1 = xn - f(xn)/f'(xn) , which is the formula for Newton's method. The formula for Newton's method works in cases where the function is differentiable, and where the gradient is not equal to zero.
Nyasha Madavo, VBA Developer.net
How To Code the Newton-Raphson Method in Excel VBA
How To Code the Newton-Raphson Method in Excel VBA
VBA implementation of Newton's algorithm
Here is an implementation of Newton's algorithm for a simple function, f(x) = x2 - 3. For the volatility surface version, func(x_n) will be replaced by the Black Scholes VBA pricing function, and func_dash(x_n) will be replaced by the VBA function for calculating vega, the first derivative of the option price with respect to volatility. Function Newton(Seed As Double, Precision As Double) As Double Dim x_next As Double, x_n As Double, error_val As Double Dim ctr As Integer x_n = Seed ctr = 0 Do x_next = x_n - func(x_n) / func_dash(x_n) error_val = x_next - x_n x_n = x_next ctr = ctr + 1 Loop Until (Abs(error_val) <= Precision Or ctr = 1000) Newton = x_next End Function Function func(x_n) As Double func = x_n ^ 2 - 3 End Function Function func_dash(x_n) As Double func_dash = 2 * x_n End Function
How VBA Developer.net Can Save You Time and money
You can get complete Excel apps from VBA Develeoper.net containing the code in this document, customisation, VBA development of any Excel, Access and Outlook apps, as well as C# and C++ add-ins and technical documentation.
Visit VBA Developer.net
Examples of VBA documents from VBA Developer.net
How to build a Black Scholes VBA Option Pricer
Nyasha Madavo, VBA Developer.net
How To Code the Newton-Raphson Method in Excel VBA
How To Code the Newton-Raphson Method in Excel VBA
How to build a Black Scholes C# Option Pricer How to build a Black Scholes VBA Option Pricer for FX Options How to build a Black Scholes VBA Option Pricer for Equity Options How to build a Black Scholes VBA Option Pricer using Monte Carlo Simulation How to build a Black Scholes VBA Option Pricer for Binary Options How to build a Black Scholes VBA Option Pricer for Equity Barrier Options How to build a Black Scholes VBA Option Pricer for Exotic Asian Options How to build a Black Scholes VBA Option Pricer for Exotic Lookback Options How to build an Equity Option Pricer using the Binomial Tree in Excel VBA How to code a Choleskey Decomposition in VBA (Numerical Methods for Excel) 3 ways to sort in VBA How to Code a Multivariate Value at Risk (VaR) VBA Monte Carlo Simulation How To Code the Newton-Raphson Method in Excel VBA How to Model Volatility Smiles, Volatility Term Structure and the Volatility Surface in Excel VBA How To Write Use Cases for a Portfolio Reporting VBA Tool How To Write a User Interface Model For a Portfolio Reporting VBA Tool How To Create a Semantic Object Model For a Portfolio Reporting VBA Tool How To Normalise a Database For VBA Apps How To Create a Database using SQL Scripts for a Portfolio Reporting VBA App How to Write Stored Procedures in SQL/Access/VBA for a Portfolio Reporting VBA App How to Use Cursors in SQL for a Portfolio Reporting VBA Tool How to Move Data from Access to Excel with SQL for a Portfolio Reporting VBA App
Nyasha Madavo, VBA Developer.net
How To Code the Newton-Raphson Method in Excel VBA
How To Code the Newton-Raphson Method in Excel VBA
Portfolio Reporting VBA Tool: Inserting Data into SQL/Access Databases from Excel Portfolio Reporting VBA Tool: Connecting Excel with SQL & Access Databases How To Design Classes For an Option Pricer in VBA: UML Concepts How To Design Classes for Object Orientated VBA Programming
Nyasha Madavo, VBA Developer.net
How To Code the Newton-Raphson Method in Excel VBA
You might also like
- Urban Survival Guide Digital BookDocument211 pagesUrban Survival Guide Digital BookGinger Gee100% (6)
- PI DataLink User GuideDocument166 pagesPI DataLink User GuideBalajiNo ratings yet
- Cambridge - Mathematical TriposDocument42 pagesCambridge - Mathematical TriposrndompersonNo ratings yet
- Export Data From Excel To Table Using Custom Web ADI IntegratorDocument23 pagesExport Data From Excel To Table Using Custom Web ADI Integratorvedavyas4funNo ratings yet
- SAS Macro That Reads The Filenames Available at A Particular Directory On Any FTP ServerDocument9 pagesSAS Macro That Reads The Filenames Available at A Particular Directory On Any FTP ServerSASTechiesNo ratings yet
- Introduction To MATLAB: 1. Warm-UpDocument13 pagesIntroduction To MATLAB: 1. Warm-UpHasanLatifNo ratings yet
- Functions in MATLAB: X 2.75 y X 2 + 5 X + 7 y 2.8313e+001Document21 pagesFunctions in MATLAB: X 2.75 y X 2 + 5 X + 7 y 2.8313e+001Rafflesia KhanNo ratings yet
- Ms. Word - Excel. Power PointDocument13 pagesMs. Word - Excel. Power PointTayyab AliNo ratings yet
- Python Tutorial 3.3.2. (En)Document127 pagesPython Tutorial 3.3.2. (En)Astin GengoNo ratings yet
- WxGlade ManualDocument43 pagesWxGlade ManualPetru BabalauNo ratings yet
- Numerical Methods VBA Cholesky DecompositionDocument4 pagesNumerical Methods VBA Cholesky DecompositionrndompersonNo ratings yet
- Newton-Raphson Method in Excel VBADocument2 pagesNewton-Raphson Method in Excel VBAMagno Felipe Teixeira0% (2)
- Plant 3d IsometricsDocument11 pagesPlant 3d IsometricsObra SprmNo ratings yet
- Experiment Instructions: Chemical Engineering Lab IIDocument19 pagesExperiment Instructions: Chemical Engineering Lab IIAhmed Ali100% (1)
- Sample Vba CodeDocument29 pagesSample Vba CodeMacklein Luna ReyesNo ratings yet
- Introduction to Elmer FEM SoftwareDocument44 pagesIntroduction to Elmer FEM SoftwareStjepan FrljicNo ratings yet
- Principles of Microeconomics - AttributedDocument1,128 pagesPrinciples of Microeconomics - AttributedAlfonso J Sintjago100% (1)
- M5 Financial Modelling For Mining Companies PDFDocument3 pagesM5 Financial Modelling For Mining Companies PDFPradita Astarina100% (1)
- Data Journalism HeistDocument43 pagesData Journalism HeistKaterina SergidouNo ratings yet
- Excel 2022 The Complete Tutorial For Beginners and Expert (Campbell, Curtis)Document209 pagesExcel 2022 The Complete Tutorial For Beginners and Expert (Campbell, Curtis)zareffueNo ratings yet
- ENDOG v4.8 Users ManualDocument45 pagesENDOG v4.8 Users Manuallittlecedar100% (1)
- BookPythonForControl PDFDocument102 pagesBookPythonForControl PDFTural CherkesgillerNo ratings yet
- CurveSelect - TheDocument22 pagesCurveSelect - TheRaúl LópezNo ratings yet
- AboveAverage ObjectDocument36 pagesAboveAverage ObjectJosef AnthonyNo ratings yet
- Southern College Visual Basic .NET Final ExamDocument7 pagesSouthern College Visual Basic .NET Final ExamBetty Nakibuuka0% (1)
- Modeling A Composition PDF TransportDocument22 pagesModeling A Composition PDF TransportMohamad PoortoosiNo ratings yet
- Top Ten Reasons To Use Openroads Technology: 1. Use Data Throughout Project Life-CycleDocument2 pagesTop Ten Reasons To Use Openroads Technology: 1. Use Data Throughout Project Life-Cycleadhimalik22No ratings yet
- Lecture2 NotesDocument17 pagesLecture2 NotesQamar SultanaNo ratings yet
- MAT005-Lab-Exercise-3Document3 pagesMAT005-Lab-Exercise-3junalynnerosaNo ratings yet
- Solving Equations (Finding Zeros)Document20 pagesSolving Equations (Finding Zeros)nguyendaibkaNo ratings yet
- Calc 1 Lecture Notes Section 3.1 1 of 8Document8 pagesCalc 1 Lecture Notes Section 3.1 1 of 8masyuki1979No ratings yet
- EEE 822 - Numerical Methods Laboraotry ManualDocument14 pagesEEE 822 - Numerical Methods Laboraotry ManualSabuj AhmedNo ratings yet
- Matlab Tutorial: Introduction to the FundamentalsDocument10 pagesMatlab Tutorial: Introduction to the Fundamentalsmysteriosan454No ratings yet
- JAVA Math-FunctionsDocument15 pagesJAVA Math-FunctionsHaryadi IndrajayaNo ratings yet
- Linear Control System LabDocument18 pagesLinear Control System LabMuhammad Saad Abdullah100% (1)
- Nonlinear Systems ScilabDocument12 pagesNonlinear Systems ScilabCarlos Soza RossNo ratings yet
- Numerical Analysis TechniquesDocument36 pagesNumerical Analysis TechniquesDembeoscarNo ratings yet
- LAB 3 Manual - Bisection MethodDocument5 pagesLAB 3 Manual - Bisection Methodmuzahir.ali.baloch2021No ratings yet
- R ExercisesDocument35 pagesR ExercisesAti SundarNo ratings yet
- Lab 02Document13 pagesLab 02T XombiNo ratings yet
- Notes On MATLABDocument26 pagesNotes On MATLABSVR07No ratings yet
- Numerical Analysis Lab ManualDocument49 pagesNumerical Analysis Lab ManualHazrat Hayat Khan0% (2)
- Lecture 7Document8 pagesLecture 7Lokeshraja SundaramNo ratings yet
- 5.4 Independence, Span and BasisDocument21 pages5.4 Independence, Span and BasisBen PhearNo ratings yet
- Arnold Ordinary Differential Equations Using MATLABDocument237 pagesArnold Ordinary Differential Equations Using MATLABKiran ManoharanNo ratings yet
- MWN 780 Assignment1 Block 1Document5 pagesMWN 780 Assignment1 Block 1DenielNo ratings yet
- Bisection MethodDocument9 pagesBisection MethodAtika Mustari SamiNo ratings yet
- Introduction To M: AtlabDocument8 pagesIntroduction To M: AtlabjayantabhbasuNo ratings yet
- Cientific Omputing: Fusen LinDocument16 pagesCientific Omputing: Fusen LinDana MckenzieNo ratings yet
- Lab 2Document14 pagesLab 2Tahsin Zaman TalhaNo ratings yet
- Simple Problems For PracticeDocument7 pagesSimple Problems For PracticeKarthik ReddyNo ratings yet
- Application of DifferentiationDocument57 pagesApplication of DifferentiationMaryati Doank0% (1)
- Math T 2Document13 pagesMath T 2Sarman TamilselvanNo ratings yet
- Mat C ManualDocument8 pagesMat C ManualBi8ikityNo ratings yet
- Sorting Vba Bubble Insertion QuickDocument6 pagesSorting Vba Bubble Insertion QuickswuswoNo ratings yet
- Lab sheet 00 Introduction to MATLABDocument9 pagesLab sheet 00 Introduction to MATLABSREELEKHA K RNo ratings yet
- ELEN E3084: Signals and Systems Lab Lab II: Introduction To Matlab (Part II) and Elementary SignalsDocument20 pagesELEN E3084: Signals and Systems Lab Lab II: Introduction To Matlab (Part II) and Elementary SignalsWael BazziNo ratings yet
- Derivation of The MethodDocument7 pagesDerivation of The MethodNipun UmatNo ratings yet
- F (X) Is ReviewedDocument18 pagesF (X) Is ReviewedSumedh KakdeNo ratings yet
- L03 NMCP Lecture03-1588102457Document30 pagesL03 NMCP Lecture03-1588102457jorgeNo ratings yet
- Lab IAT 03Document17 pagesLab IAT 03igorkapganglinkNo ratings yet
- Chap 2Document30 pagesChap 2Sharif M Mizanur RahmanNo ratings yet
- λ-Calculus: a Turing machine."-Alonzo ChurchDocument13 pagesλ-Calculus: a Turing machine."-Alonzo ChurchBrianNo ratings yet
- Lab Experiment 1 (A)Document14 pagesLab Experiment 1 (A)Laiba MaryamNo ratings yet
- 3.5 Coefficients of The Interpolating Polynomial: Interpolation and ExtrapolationDocument4 pages3.5 Coefficients of The Interpolating Polynomial: Interpolation and ExtrapolationVinay GuptaNo ratings yet
- Getting Help For FunctionsDocument86 pagesGetting Help For Functionskurddoski28No ratings yet
- MATLAB Tutorial: MATLAB Basics & Signal Processing ToolboxDocument47 pagesMATLAB Tutorial: MATLAB Basics & Signal Processing ToolboxSaeed Mahmood Gul KhanNo ratings yet
- MATLAB Lecture 3. Polynomials and Curve Fitting PDFDocument3 pagesMATLAB Lecture 3. Polynomials and Curve Fitting PDFTan HuynhNo ratings yet
- LAB-2 Digital Signal ProcessingDocument11 pagesLAB-2 Digital Signal ProcessingyohanNo ratings yet
- Chbe 553 Notes 1Document6 pagesChbe 553 Notes 1सुबेदी गौरवNo ratings yet
- Vector OperationDocument6 pagesVector OperationUsman BajwaNo ratings yet
- Technical Computing Laboratory ManualDocument54 pagesTechnical Computing Laboratory ManualKarlo UntalanNo ratings yet
- NOVEL RESEARCH - Emily Bronte - Wuthering HeightsDocument283 pagesNOVEL RESEARCH - Emily Bronte - Wuthering HeightsrndompersonNo ratings yet
- Black Scholes FX Options PricingDocument5 pagesBlack Scholes FX Options PricingrndompersonNo ratings yet
- Gamma FitDocument10 pagesGamma FitFajar Premana PutraNo ratings yet
- ForecastX Wizard User GuideDocument220 pagesForecastX Wizard User GuidealimNo ratings yet
- Excel Spreadsheet Basics: Formulas, Tables, Charts in 40 CharactersDocument35 pagesExcel Spreadsheet Basics: Formulas, Tables, Charts in 40 CharactersJerry HalibasNo ratings yet
- How To Add Pandas To Spyder?: Ans-Import Pandas As PDDocument3 pagesHow To Add Pandas To Spyder?: Ans-Import Pandas As PDHalder SubhasNo ratings yet
- Extract TextDocument95 pagesExtract Textsrinu chill333No ratings yet
- Nutrient Requirements of Swine: Eleventh Revised Edition: Model User GuideDocument16 pagesNutrient Requirements of Swine: Eleventh Revised Edition: Model User GuideEduardo ViolaNo ratings yet
- RGB ImportDocument5 pagesRGB ImportAamir LokhandwalaNo ratings yet
- Method of Deriving The PolynomialDocument17 pagesMethod of Deriving The PolynomialsreedharNo ratings yet
- Optimization of Cargo Container Loading On Railway WagonsDocument6 pagesOptimization of Cargo Container Loading On Railway Wagonsaxyy100% (1)
- Process To Export Test Plans From Excel Into Quality Center: 1. Install and Configure The Microsoft Excel Add-InDocument15 pagesProcess To Export Test Plans From Excel Into Quality Center: 1. Install and Configure The Microsoft Excel Add-InmvnagaNo ratings yet
- Davidoff - Moving Data Into EViews v2Document9 pagesDavidoff - Moving Data Into EViews v2YAHYA BIN SAININo ratings yet
- Rani PorandlaDocument3 pagesRani PorandlabhadrakaliagreementsNo ratings yet
- Nabertherm L 15/12 Muffle Furnace OfferDocument15 pagesNabertherm L 15/12 Muffle Furnace OfferRidouane EL HAJJINo ratings yet
- Foosball GanttDocument14 pagesFoosball Ganttapi-551074283No ratings yet
- PRACTICAL FILE ENGINEERING SYSTEM MODELLING & SIMULATION LAB FILEDocument41 pagesPRACTICAL FILE ENGINEERING SYSTEM MODELLING & SIMULATION LAB FILEShubham Sharma0% (1)
- EViews 6 Command RefDocument926 pagesEViews 6 Command Refrbm0101No ratings yet
- Case Study of Building A Data Warehouse With Analysis ServicesDocument10 pagesCase Study of Building A Data Warehouse With Analysis ServicesbabussnmcaNo ratings yet
- Lab Mannual Spss FinalDocument67 pagesLab Mannual Spss Finalajay_anavNo ratings yet
- Course Syllubus and Overview Ica 2016Document1 pageCourse Syllubus and Overview Ica 2016api-358760405No ratings yet
- Research Paper Worksheets PDFDocument8 pagesResearch Paper Worksheets PDFfyr60xv7100% (1)