Professional Documents
Culture Documents
05 ContinuousRV 1206
Uploaded by
Anonymous KUuLddnO98Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
05 ContinuousRV 1206
Uploaded by
Anonymous KUuLddnO98Copyright:
Available Formats
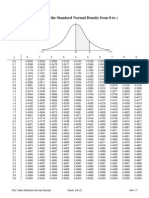
p.
5-31
Summary for X ~ Normal(, o
2
)
Pdf:
Cdf: no close form, but usually denoted by u((x)/o).
Parameters: R and o>0.
Mean: E(X) = .
Variance: Var(X) = o
2
.
f(x) =
1
2
e
(x)
2
2
2
, < x < ,
Weibull Distribution
For o, |>0 and vR, the function
f(x) =
(
1
e
(
x
, if x ,
0, if x < ,
is a pdf since (1) f(x) 0 for all x R, and (2)
R
f(x) dx =
R
1
e
(
x
dx
=
R
0
e
y
dy = e
y
|
0
= 1.
p. 5-32
The distribution of a random variable X with this pdf is
called the Weibull distribution with parameters o, |, and v .
(exercise) The cdf of Weibull distribution is
F(x) =
(
1 e
(
x
, if x ,
0, if x < .
Theorem. The mean and variance of a Weibull distribution with
parameter o, |, and v are
=
1 +
1
+ and
2
=
2
1 +
2
1 +
1
i
2
.
E(X) =
R
v
x
1
e
(
x
dx
=
R
0
(y
1/
+)e
y
dy
=
R
0
y
1/
e
y
dy +
R
0
e
y
dy =
+ 1
+
Proof.
E(X
2
) =
R
v
x
2
1
e
(
x
dx
=
R
0
(y
1/
+ )
2
e
y
dy
=
2
R
0
y
2/
e
y
dy + 2
R
0
y
1/
e
y
dy +
2
R
0
e
y
dy
=
2
+ 1
+ 2
+ 1
+
2
NTHU MATH 2810, 2011 Lecture Notes
made by Shao-Wei Cheng (NTHU, Taiwan)
p. 5-33
Some properties
Weibull distribution is widely used to
model lifetime.
o: scale parameter; |: shape parameter;
v: location parameter
Theorem. If X~exponential(), then
is distributed as Weibull with parameter o, |, and v (exercise).
Y = (X)
1/
+
Cauchy Distribution
For R and o>0, the function
f(x) =
2
+(x)
2
, < x < ,
is a pdf since (1) f(x) 0 for all x R, and (2)
The distribution of a random variable X with this pdf is
called the Cauchy distribution with parameters and o,
denoted by Cauchy(, o).
R
f(x) dx =
R
2
+(x)
2
dx
=
R
1
1+y
2
dy =
1
tan
1
(y)
= 1.
p. 5-34
The mean and variance of Cauchy distribution do not exist
because the integral does not converge absolutely
Some properties
Cauchy is a heavy tail distribution
: location parameter; o: scale parameter
Theorem. If X~Cauchy(, o), then
aX+b~Cauchy(a+b, |a|o). (exercise)
The cdf of Cauchy distribution is
for <x<. (exercise)
Reading: textbook, Sec 5.4, 5.5, 5.6
F(x) =
R
x
2
+(y)
2
dy =
1
2
+
1
tan
1
x
NTHU MATH 2810, 2011 Lecture Notes
made by Shao-Wei Cheng (NTHU, Taiwan)
You might also like
- Differential Entropy ExplainedDocument29 pagesDifferential Entropy ExplainedGaneshkumarmuthurajNo ratings yet
- Hw1sol PDFDocument9 pagesHw1sol PDFRohit BhadauriaNo ratings yet
- Seminar in Large Deviations and ApplicationsDocument14 pagesSeminar in Large Deviations and ApplicationsDomenique SchwestermannNo ratings yet
- Random Processes: Version 2, ECE IIT, KharagpurDocument8 pagesRandom Processes: Version 2, ECE IIT, KharagpurHarshaNo ratings yet
- Stochastic Estimation and Control LectureDocument7 pagesStochastic Estimation and Control LectureMariam MugheesNo ratings yet
- Lecture11 (Week 12) UpdatedDocument34 pagesLecture11 (Week 12) UpdatedBrian LiNo ratings yet
- Multiple solutions of Dirichlet problem with p-Laplacian and set-valued nonlinearityDocument19 pagesMultiple solutions of Dirichlet problem with p-Laplacian and set-valued nonlinearityRay GobbiNo ratings yet
- MIT Numerical PDEDocument119 pagesMIT Numerical PDEKruger JoeNo ratings yet
- Fan e Zhao - de Giorgi e Continuidade 1997 PDFDocument24 pagesFan e Zhao - de Giorgi e Continuidade 1997 PDFThiago WilliamsNo ratings yet
- Probability Laws: Complementary EventDocument23 pagesProbability Laws: Complementary EventalvinhimNo ratings yet
- Lecture 09Document15 pagesLecture 09nandish mehtaNo ratings yet
- Unit 1 - 03Document10 pagesUnit 1 - 03Raja RamachandranNo ratings yet
- Pairs of Random VariablesDocument69 pagesPairs of Random Variablest_man222No ratings yet
- Generating Random VariablesDocument7 pagesGenerating Random VariablesTsvetanNo ratings yet
- Functions Domains and Ranges GuideDocument21 pagesFunctions Domains and Ranges GuideEdge of ScenesNo ratings yet
- Expectation: Moments of A DistributionDocument39 pagesExpectation: Moments of A DistributionDaniel Lee Eisenberg JacobsNo ratings yet
- The Uniform DistributnDocument7 pagesThe Uniform DistributnsajeerNo ratings yet
- Partial Differential EquationsDocument11 pagesPartial Differential EquationsSaadFarooqNo ratings yet
- 2021 Spring Nonlinear Techniques For Nonlinear Dispersive PDEs 4Document10 pages2021 Spring Nonlinear Techniques For Nonlinear Dispersive PDEs 4chejianglongNo ratings yet
- Solutions To Problem Set 2: P (E) + DPDocument12 pagesSolutions To Problem Set 2: P (E) + DPlantea1No ratings yet
- Basics of Wavelets: Isye8843A, Brani Vidakovic Handout 20Document27 pagesBasics of Wavelets: Isye8843A, Brani Vidakovic Handout 20Abbas AbbasiNo ratings yet
- Chapter 2 - Random VariablesDocument26 pagesChapter 2 - Random VariablesNikhil SharmaNo ratings yet
- Quadratic Mean Differentiability ExampleDocument5 pagesQuadratic Mean Differentiability ExamplemamurtazaNo ratings yet
- Applied Probability Lecture Notes (OS2103Document22 pagesApplied Probability Lecture Notes (OS2103Tayyab ZafarNo ratings yet
- OU Open University SM358 2009 Exam SolutionsDocument23 pagesOU Open University SM358 2009 Exam Solutionssam smithNo ratings yet
- Improper Integral1Document25 pagesImproper Integral1Lev DunNo ratings yet
- Ellipsoid PotentialDocument18 pagesEllipsoid PotentialEduardoHenriquezNo ratings yet
- Conformal Field NotesDocument7 pagesConformal Field NotesSrivatsan BalakrishnanNo ratings yet
- JMM Volume 7 Issue 2 Pages 231-250Document20 pagesJMM Volume 7 Issue 2 Pages 231-250milahnur sitiNo ratings yet
- Tmna 125 2 413Document13 pagesTmna 125 2 413Simone SecchiNo ratings yet
- Assignment 4 SolutionsDocument5 pagesAssignment 4 Solutionshlove1No ratings yet
- Quantum Tunneling Through A BarrierDocument12 pagesQuantum Tunneling Through A Barrierjasmine-rNo ratings yet
- Probability distributions and sampling formulasDocument8 pagesProbability distributions and sampling formulasAlan TruongNo ratings yet
- Partial DifferentiationDocument9 pagesPartial Differentiationsanoj kumarNo ratings yet
- Understanding the Expectation of a Random VariableDocument15 pagesUnderstanding the Expectation of a Random VariableLibyaFlowerNo ratings yet
- EN007001 Engineering Research Methodology: Statistical Inference: Bayesian InferenceDocument72 pagesEN007001 Engineering Research Methodology: Statistical Inference: Bayesian Inferenceคงเดช คํานึกNo ratings yet
- Solution:: Probability Assignment - I Name: Soumya Dasgupta (BMC202042)Document2 pagesSolution:: Probability Assignment - I Name: Soumya Dasgupta (BMC202042)Soumya Das guptaNo ratings yet
- Paramest PDFDocument37 pagesParamest PDFMouhamadou DiabyNo ratings yet
- Continuous Distributions: Section 2Document27 pagesContinuous Distributions: Section 2eng ineera100% (1)
- SPH Models For Geo-Disasters: 2.1 Basic Concept of SPHDocument28 pagesSPH Models For Geo-Disasters: 2.1 Basic Concept of SPHManish Kumar SinghNo ratings yet
- Mathematical Statistics (MA212M) : Lecture SlidesDocument8 pagesMathematical Statistics (MA212M) : Lecture SlidesakshayNo ratings yet
- 110 Normal DistributionDocument5 pages110 Normal DistributionCesarNo ratings yet
- MATH 300 Fall 2004 Advanced Boundary Value Problems I Solutions To Sample Final Exam Friday December 3, 2004Document6 pagesMATH 300 Fall 2004 Advanced Boundary Value Problems I Solutions To Sample Final Exam Friday December 3, 2004tehepiconeNo ratings yet
- 2006 Jessen - Mikosch Regularly Varying FunctionsDocument22 pages2006 Jessen - Mikosch Regularly Varying FunctionsJonas SprindysNo ratings yet
- Orthogonal P-Wavelets On R: + Yu.A. FarkovDocument23 pagesOrthogonal P-Wavelets On R: + Yu.A. FarkovukoszapavlinjeNo ratings yet
- Meshless and Generalized Finite Element Methods: A Survey of Some Major ResultsDocument20 pagesMeshless and Generalized Finite Element Methods: A Survey of Some Major ResultsJorge Luis Garcia ZuñigaNo ratings yet
- Solutions To Fall 2006 Math 301 Midterm Problems: N M 1 N NDocument4 pagesSolutions To Fall 2006 Math 301 Midterm Problems: N M 1 N NJacky PoNo ratings yet
- School of Mathematics and Physics, The University of QueenslandDocument1 pageSchool of Mathematics and Physics, The University of QueenslandVincent LiuNo ratings yet
- Two-Dimensional Random VariablesDocument13 pagesTwo-Dimensional Random VariablesAllen ChandlerNo ratings yet
- Construction of Wavelet Packets On P-Adic FieldDocument14 pagesConstruction of Wavelet Packets On P-Adic FieldukoszapavlinjeNo ratings yet
- Regression and Probability Concepts for StatisticsDocument1 pageRegression and Probability Concepts for StatisticsgadihokNo ratings yet
- Applied Mathematics Letters: S.A. MohiuddineDocument5 pagesApplied Mathematics Letters: S.A. MohiuddineshivaniNo ratings yet
- Numerical computation of finite-genus KdV solutions via Riemann-Hilbert problemsDocument7 pagesNumerical computation of finite-genus KdV solutions via Riemann-Hilbert problemsDamian ButtsNo ratings yet
- Entropy of The Gaussian Distribution: Appendix ADocument5 pagesEntropy of The Gaussian Distribution: Appendix ABoyan Ivanov BonevNo ratings yet
- Lagrange TheoremDocument10 pagesLagrange Theoremyay111No ratings yet
- Mathematics 315 - Assignment 1: X A X A X A X A X ADocument4 pagesMathematics 315 - Assignment 1: X A X A X A X A X ATom DavisNo ratings yet
- Green's Function Estimates for Lattice Schrödinger Operators and Applications. (AM-158)From EverandGreen's Function Estimates for Lattice Schrödinger Operators and Applications. (AM-158)No ratings yet
- Mathematics 1St First Order Linear Differential Equations 2Nd Second Order Linear Differential Equations Laplace Fourier Bessel MathematicsFrom EverandMathematics 1St First Order Linear Differential Equations 2Nd Second Order Linear Differential Equations Laplace Fourier Bessel MathematicsNo ratings yet
- Difference Equations in Normed Spaces: Stability and OscillationsFrom EverandDifference Equations in Normed Spaces: Stability and OscillationsNo ratings yet
- 2 Permutations, Combinations, and The Binomial TheoremDocument11 pages2 Permutations, Combinations, and The Binomial TheoremChrisRyanBabasSulayaoNo ratings yet
- Vancouver Reference Style PDFDocument24 pagesVancouver Reference Style PDFAndini PramonoNo ratings yet
- PHYF144 Tutorial Questions UpdatedDocument16 pagesPHYF144 Tutorial Questions UpdatedAnonymous KUuLddnO98No ratings yet
- Maple 11 TutorialDocument40 pagesMaple 11 TutorialAlfianInziaFusiariNo ratings yet
- PoetryDocument1 pagePoetryAnonymous KUuLddnO98No ratings yet
- Google Maps Bukit Moko PDFDocument1 pageGoogle Maps Bukit Moko PDFAnonymous KUuLddnO98No ratings yet
- Tabel FourierDocument3 pagesTabel FourierAnonymous KUuLddnO98No ratings yet
- Love Curve With Maple 16.1Document1 pageLove Curve With Maple 16.1Anonymous KUuLddnO98No ratings yet
- Adams Bash Forth ProofDocument5 pagesAdams Bash Forth ProofpiticmicNo ratings yet
- Probability Distribution Function and ShapeDocument6 pagesProbability Distribution Function and ShapeAnonymous KUuLddnO98No ratings yet
- Tabel Distribusi Normal BakuDocument1 pageTabel Distribusi Normal BakuAnonymous KUuLddnO9867% (6)
- Computation of Test Statistic On Population MeanDocument27 pagesComputation of Test Statistic On Population Meannot deniseNo ratings yet
- Unit Chi-Square Test For Nominal Data: 20.0 ObjectivesDocument7 pagesUnit Chi-Square Test For Nominal Data: 20.0 ObjectivesNarayanan BhaskaranNo ratings yet
- Biostatistics of HKU MMEDSC Session5handoutprint3Document28 pagesBiostatistics of HKU MMEDSC Session5handoutprint3Xin chao LiNo ratings yet
- Exploratory Data Analysis Techniques for Data InsightsDocument790 pagesExploratory Data Analysis Techniques for Data InsightsTesisTraduccionesRuzel100% (2)
- Sampling and Sampling Distributions: ASW, Chapter 7Document25 pagesSampling and Sampling Distributions: ASW, Chapter 7Andi HarismahyantiNo ratings yet
- The Trinomial Distribution ExplainedDocument2 pagesThe Trinomial Distribution Explainednitin30No ratings yet
- Using R for nonparametric analysis of binomial and normal distributionsDocument9 pagesUsing R for nonparametric analysis of binomial and normal distributionsblaznspadzNo ratings yet
- Poison DistributionDocument6 pagesPoison DistributiondhwanitNo ratings yet
- Random Variables and Probability DistributionsDocument40 pagesRandom Variables and Probability DistributionsManishNo ratings yet
- Statistics Mcqs - Tests For Qualitative Data Part 1: ExamraceDocument7 pagesStatistics Mcqs - Tests For Qualitative Data Part 1: Examracemaqsood yaqoobNo ratings yet
- Practical Research 2Document24 pagesPractical Research 2Beneva Vega MalabananNo ratings yet
- Stage 8 End of Unit 13 WorksheetDocument3 pagesStage 8 End of Unit 13 WorksheetDeena100% (1)
- Exam Cheatsheet For R Langauge CodingDocument2 pagesExam Cheatsheet For R Langauge CodingamirNo ratings yet
- What Does A Statistical Test DoDocument16 pagesWhat Does A Statistical Test DoRenato PanesNo ratings yet
- Refresher (Probability)Document2 pagesRefresher (Probability)sadonNo ratings yet
- MA8402 Probability and Queueing MCQDocument18 pagesMA8402 Probability and Queueing MCQMohammed HasheemNo ratings yet
- Probability MethodsDocument106 pagesProbability MethodsebrarrsevimmNo ratings yet
- Introduction To StatisticsDocument43 pagesIntroduction To StatisticsLee Min Mark XXVI100% (2)
- Probability and Statistics Tutorial for EQT 272Document2 pagesProbability and Statistics Tutorial for EQT 272Jared KuyislNo ratings yet
- Class 5 ESEI Maths L5 Hypothesis TestingDocument71 pagesClass 5 ESEI Maths L5 Hypothesis TestingPhilip TrrrNo ratings yet
- Stat 130n Answers To The LAs in Lessons 3.1-3.3Document18 pagesStat 130n Answers To The LAs in Lessons 3.1-3.3Faith GarfinNo ratings yet
- Practical Research 2 Q2 Module 6 7Document32 pagesPractical Research 2 Q2 Module 6 7Rosita Antiquina Elopre100% (2)
- FormulasDocument21 pagesFormulasSamantha Marie RebolledoNo ratings yet
- UNIT II Probability Distribution 1Document33 pagesUNIT II Probability Distribution 1AcchyutjhNo ratings yet
- Statistics SummaryDocument10 pagesStatistics SummaryAhmed Kadem ArabNo ratings yet
- Stat-Q2 1Document8 pagesStat-Q2 1Von Edrian PaguioNo ratings yet
- Econ 15B - Test 1 - June 29, 2018Document3 pagesEcon 15B - Test 1 - June 29, 2018pwnageownsuNo ratings yet
- 3.6: General Hypothesis TestsDocument6 pages3.6: General Hypothesis Testssound05No ratings yet
- Econometrics 2 Exam AnswersDocument6 pagesEconometrics 2 Exam AnswersDavide Rossetti67% (3)
- Statistical Analysis of Wholesale Customers and CMSU SurveyDocument21 pagesStatistical Analysis of Wholesale Customers and CMSU Surveyhepzi selvam100% (1)