Todo de Discretas

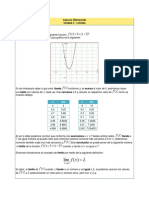
Unidad I: Introducción a la lógica Álgebra de proposiciones
LAS MATEMÁTICAS DE LA COMPUTACIÓN

UNA INTRODUCCIÓN
UNIDAD I: INTRODUCCIÓN A LA LÓGICA
1.1 Conceptos y definiciones

1.1.1 Cálculo proposicional.
1.1.2 Conectores lógicos.
1.1.3 Tautologías, contradicciones y contingencias.
1.1.4 Equivalencias lógicas.
1.1.5 Álgebra de proposiciones.
1.2. Inferencia Lógica

1.2.1 Definiciones básicas.
1.2.2 Leyes de la inferencia.
1.2.3 Demostración de argumentos.
1.3 Funciones lógicas y cuantificadores

1.3.1 Funciones lógicas y conjunto de validez.
1.3.2 Uso de cuantificadores: Función de una, dos y tres variables.
1.1 CONCEPTOS Y DEFINICIONES
1.1.1 Cálculo proposicional
La lógica estudia las formas del pensamiento desde el punto de vista de su estructura;
esto es, analiza las relaciones entre las proposiciones (o enunciados) y no el contenido de
éstas; en particular se analiza la veracidad o falsedad de un razonamiento.
Los razonamientos lógicos se utilizan en áreas como: matemática (para realizar pruebas
matemáticas, demostrar teoremas etc), derecho (para dar argumentos legales que demuestren
la culpabilidad o inocencia de una persona, etc.), vida cotidiana ( para explicar las razones por
las que salimos mal en un examen, por las que llegamos tarde a casa, etc.) en computación
(par demostrar que los programas hacen precisamente lo que deberían hacer o bien lo que
queremos que hagan); en general se usan en cualquier hecho que involucre un conjunto de
hipótesis.
En el desarrollo de cualquier teoría, se hacen afirmaciones en forma de oraciones. Tales

afirmaciones pueden ser proposiciones o no.
Definición 1.1.1 (Proposición)

Una proposición es una oración declarativa que puede ser verdadera o falsa pero no
ambas. En general, una proposición se expresa como una afirmación declarativa y no como
una pregunta o una instrucción (orden). Una proposición también se llama enunciado.
Una introducción a las matemáticas de la computación

22
Notación: las proposiciones generalmente se representan con las letras minúsculas p, q, r, etc.
Sin embargo algunos autores simbolizan las proposiciones con letras mayúsculas como son P,
Q, R y hasta por A, B, C, ... En este libro usaremos letras minúsculas para denotar las
proposiciones. Además, usaremos p: 2<5, para indicar que p es la proposición “2 es menor
que 5, 2 < 5”.
Definición 1.1.2 (Valor de verdad)

Se denomina valor de verdad de una proposición a la veracidad o falsedad de la
proposición o enunciado. El valor de verdad de algunas proposiciones depende del lugar y del
tiempo.
Ejemplo 1.1.1
a) Oraciones que son proposiciones.
p: Una decena tiene 10 unidades.
q: México está en Europa.
r: 2 + 2 = 3.
s: El hombre llegó a la luna en el año 2000.
t: la tierra es redonda.
u: El número 9 es primo.
v: 2 + 3 es un número par.
w: 15 es divisible por 7.
x: 2 > 5.
y: Dante escribió la “Divina Comedia”.
z: Hoy es lunes
Observe que cada una de estas oraciones puede ser calificada como falsa o verdadera.
b) Oraciones que no son proposiciones.

p: 1 + 1.
q: ¿Qué día es hoy?.
r: Borra el pizarrón.
s: La tierra es el único planeta del universo que tiene vida.
t: Este enunciado es falso.
u: El hombre llegará a Marte en el año 2005.
v: ¿Cómo estás?.
w: Levántate y desayuna.
x: Compra dos helados.
y: x + 2 = 5.
z: ¿Quieres ser mi novia?.
Proposición Razón
P No tiene sentido.
q, v, z Está expresada en forma de pregunta y una pregunta no puede ser
calificada como falsa o verdadera.
r, w, x Está expresada en forma de orden y una orden no puede ser calificada

23
como falsa o verdadera.

s Es ambigua, la respuesta depende de quien la conteste.
t No se conoce el enunciado al cual se hace referencia.
u Es necesario estar en un año posterior al 2005 para asignar un valor de
verdad.
y Es necesario conocer el valor de x para asignar un valor de verdad a la
proposición.
Ejemplo 1.1.2
Determine si las siguientes oraciones son proposiciones; si son proposiciones establezca
su valor de verdad.
Oración Proposición (Si/No) Valor de verdad

a) p: 2 es un número irracional. Si (Verdadera)
b) q: 2 + 3 es un número par. Si (Falsa)
c) r: 5-3. No
d) s: 4 es un múltiplo de 12. Si (Falsa)
e) t: ¡Hola! No
f) u: ¿Terminaste tu tarea? No
g) v: 2 es un número primo. Si (Verdadera)
h) w: x -1 > 5. No
i) x: 4+1 = 5 Si (Verdadera)
j) y: 15 es un número primo Si (Falsa)
El valor de verdad de las proposiciones del ejemplo 1.2, no dependen del lugar ni del
tiempo, sin embargo si se considera la proposición “ hoy es lunes ” el valor de verdad de esta
proposición dependerá del tiempo, esto es, si hoy es lunes, entonces la proposición es
verdadera, pero, si hoy es martes la proposición es falsa. Lo mismo ocurre con las
proposiciones: “está lloviendo”, “hace frío”, etc.
1.1.2 Conectores lógicos
Las proposiciones pueden ser:

Simples.
Compuestas.
Definición 1.1.3 (Proposición simple)

Es una proposición que no puede descomponerse en algo más sencillo, es decir, son
proposiciones formadas por una sola oración.
Definición 1.1.4 (Proposición compuesta)

Es una proposición que se forma a partir de dos o más proposiciones simples, las cuales
se unen por conectivos de enlace. Estos conectivos de enlace se conocen como conectivos
lógicos.

24
La forma de las proposiciones compuestas depende del término de enlace utilizado, y no

del contenido de la proposición o proposiciones simples.
Definición 1.1.5 (Conectivos lógicos)

Los conectivos lógicos son signos, con significado, que tienen como función enlazar una
proposición simple con otra, con el fin de construir proposiciones compuestas.
Conectivos lógicos
Negación.
Conjunción.
Disyunción.
Implicación o condicional.
Doble implicación o bicondicional.
Los valores de verdad de las proposiciones compuestas, pueden describirse mediante

tablas de verdad.
Definición 1.1.6 (Tabla de verdad)

La tabla de verdad de una proposición compuesta p formada por las proposiciones
simples p1, p2, ..., p n enlista todas las combinaciones posibles de los valores de verdad para p1,
p2, ..., p n, donde 1 (uno) indica verdadero y 0 (cero) indica falso, de modo que para cada una
de estas combinaciones se indica el valor de verdad de p.
Definición 1.1.7 (Negación)

Si p es una proposición, se puede formar la negación de p, usando algunas de las
siguientes palabras de enlace:
No...
No es cierto que...
Es falso que...
No ocurre que...
No sucede que...
No es el caso que...
precediendo esta frase a la proposición p, o si es posible insertando en p la palabra no. La

negación se denota por p ( o bien por p, p o por p’ ) y se lee como “no p”. En este libro en
particular usaremos la notación p para indicar la negación de una proposición.
Si el valor de verdad de una proposición p es verdadero (1), entonces el valor de verdad

de la negación de p ( p ) es falso (0) y si el valor de verdad de p es falso (0), entonces el valor
de verdad de p es verdadero (1). El valor de verdad de la negación de una proposición se
resume en la siguiente tabla de verdad.
Tabla de verdad ( p )

25
p p
0 1
1 0
Ejemplo 1.1.3
Sea p: El agua es incolora.
La negación de p es una proposición que puede escribirse como:
p : El agua no es incolora.
p : No es el caso que el agua es incolora.
p : No sucede que el agua es incolora.
p : No ocurre que el agua es incolora.
Como el valor de verdad de la proposición p es verdadero, p es falsa. En el lenguaje

común normalmente usamos la expresión “el agua no es incolora”. Dado que p es una
proposición, podemos expresar la negación de ésta como: ( p ) : No es cierto que el agua no es
incolora. Sabemos que el valor de verdad de p es falso por tanto el valor de verdad de ( p ) es
verdadero.
Ejemplo 1.1.4
q: Hoy es martes.
q : Hoy no es martes.
q : No es cierto que hoy es martes.
q : Es falso que hoy es martes.
q : No ocurre que hoy es martes.
El valor de verdad de esta proposición depende del tiempo.
Si q es falso, q es verdadero.
Si q es verdadero, q es falso.
(q ) : Es falso que hoy no es martes: hoy es martes.
Ejemplo 1.1.5
Proposición Valor de verdad Negación Valor de verdad
a) s: 2 < 5. 1 s:2 5 0
b) t: 3 es múltiplo de 6. 0 t : 3 no es múltiplo de 6 1
Definición 1.1.8 (Conjunción)

La conjunción de las proposiciones p y q se puede formar usando algunas de las
siguientes palabras de enlace:
Y... Pero...
Aunque... Sin embargo...

26
Como... Aún...
A la vez... No obstante...
A pesar de... Tanto ... como...
Y se denota por p q que se lee “p y q”.
Si se conjuntan dos proposiciones que efectivamente sean verdaderas – ambas- se

obtiene una proposición compuesta verdadera. Pero si se conjuntan dos proposiciones y una es
falsa o las dos, se obtendrá entonces una proposición falsa.
Resumimos el valor de verdad de la conjunción de dos proposiciones en la siguiente

tabla de verdad.
Tabla de verdad (p q )
p q p q
0 0 0
0 1 0
1 0 0
1 1 1
Ejemplo 1.1.6
a) Considere las proposiciones p y q definidas como: p: 5<7, q: 9>3
Entonces la conjunción de p y q puede escribirse como:
p q :5 <7 y 9>3.
p q : 5<7 pero 9>3.
p q : 5<7 aunque 9>3.
p q : 5<7 sin embargo 9>3.
Como las proposiciones p y q son verdaderas p q también es verdadera.
b) r: El basic es un lenguaje de programación

s: El pascal es un lenguaje de programación
r s : El basic es un lenguaje de programación y el pascal es un lenguaje de
programación.
r s : El basic y el pascal son lenguajes de programación.
r s : Tanto el basic como el pascal son lenguajes de programación.
Como las proposiciones r y s son verdaderas r s también es verdadera.
c) m: Esta lloviendo.
n: Hace sol.
m n :Está lloviendo y hace sol.

m n :Está lloviendo pero hace sol.
m n : Está lloviendo a pesar de que hace sol.
m n : Está lloviendo no obstante hace sol.
El valor de verdad de m n depende del tiempo.
d) p: 9 es un número primo

27
q: 9 es un número impar.
p q : 9 es un número primo y 9 es un número impar.
p q : 9 es un número primo pero 9 es un número impar.
p q :9 es a la vez par e impar.
Como p es falsa y q es verdadera p q es falsa.
e) p: 2 + 2 = 4.
q: 2 x 3 = 6.
p q: 2 + 2 = 4 y 2 x 3 = 6.
Como p es verdadera y q es verdadera p q es verdadera.
f) p: Hoy es lunes
q: Está nublado
p q : No es cierto que hoy es lunes y está nublado.
p q : No es cierto que, hoy es lunes y está nublado.
El valor de verdad de estas proposiciones depende del tiempo.
La disyunción puede ser inclusiva o exclusiva.
Definición 1.1.9 (Disyunción inclusiva)

La disyunción inclusiva de las proposiciones p y q se puede formar usando la palabra de
enlace o y es la relación que se establece entre dos proposiciones indicando que al menos una
de ellas es verdadera, aunque puede ocurrir que lo sean ambas y se denota por p q, que se lee
“p o q”.
En la siguiente tabla se resume el valor de verdad de la disyunción inclusiva de dos

proposiciones.
Tabla de verdad ( p q )
p q p q
0 0 0
0 1 1
1 0 1
1 1 1
Ejemplo 1.1.7
a) p: El tigre es carnívoro. Verdadera
q: El tigre es un animal felino. Verdadera
p q : El tigre es carnívoro o el tigre es un animal felino. Verdadera
b) r: 7>2. Verdadera
s: 5<0. Falsa
r s : 7>2 o 5<0. Verdadera
c) j: 4 es par. Verdadera

28
k: 4 es impar. Falsa
l: 4 es primo. Falsa
j l: 4 es par y 4 es primo. Falsa
k l: 4 es impar y 4 es primo. Falsa
(j l) (k l): 4 es par y 4 es primo, o 4 es impar y 4 es primo. Falsa
j l : Es falso que, 4 es par y 4 es primo. Verdadera

l j : No es cierto que 4 es primo y 4 es par. Verdadera
Definición 1.1.10 (Disyunción exclusiva)

La disyunción exclusiva de las proposiciones p y q se puede formar usando las palabras
de enlace:
p...ó...q
p...o...q pero no ambas.
La disyunción exclusiva de dos proposiciones es la relación que se establece entre dos

proposiciones señalando que necesariamente una es verdadera y la otra es falsa, es decir, que
no pueden ser ambas verdaderas o ambas falsas.
Tabla de verdad (p q)
p q p q
0 0 0
0 1 1
1 0 1
1 1 0
Nota 1.1.1: Usaremos la o acentuada (ó) para diferenciar la disyunción exclusiva de la

inclusiva.
Nota 1.1.2: Observe que siempre que la disyunción exclusiva es verdadera la disyunción
inclusiva también es verdadera.
Ejemplo1.1.8
a) p: Abril tiene 30 días. Verdadera
q: Abril tiene 31 días. Falsa
p q: Abril tiene 30 días ó abril tiene 31 días Verdadera
p q: Abril tiene 30 o 31 días. Verdadera
Puede ocurrir una cosa o la otra, pero no pueden ocurrir ambas. La expresión o tiene
sentido exclusivo.
b) s: Trabajo.
t: Estudio.
s t: Trabajo o estudio pero no ambas.
El valor de verdad de estás proposiciones depende de la persona a la que se cuestione.
c) m: 2 es par. Verdadera

29
n: 2 es primo. Verdadera
m n: 2 es par o dos es primo. Verdadera
m n: 2 es par ó 2 es primo. Falsa
m n : no es cierto que, 2 es par o primo pero no ambos. Verdadera
m n : 2 no es par o 2 es primo pero no ambas. Verdadera
Definición 1.1.11 (Implicación o condicional)

La implicación o condicional de las proposiciones p y q se denota por p q que se lee
“Si p, entonces q”. Y se puede formar usando las palabras de enlace:
Si p, entonces q. p implica q.
p sólo si q. q si p.
Cuando p, q. q es una condición necesaria para p.
p es una condición suficiente para q. p luego q.
No q a menos que p. p por consiguiente q.
p por lo tanto q. p en consecuencia q.
La proposición p también se llama hipótesis, antecedente o condición suficiente, y la

proposición q, conclusión, consecuente o condición necesaria.
Nota 1.1.3: Al referirnos a los elementos constitutivos de una proposición condicional hay que
hacerlo considerando las siguientes parejas:
Hipótesis conclusión.
Antecedente consecuente.
Condición suficiente condición necesaria.
Consideremos un ejemplo de proposición condicional, y examinemos su valor de

verdad.
Ejemplo 1.1.9
Sean p: estudio q: aprobaré
p q: Si estudio, entonces aprobaré.
Asignemos valor de verdad a las proposiciones.
1) Consideremos que p es falsa y q es falsa, y consideremos la proposición condicional con

los valores de verdad indicados:
Si no estudio, entonces no aprobaré.
El valor de verdad que asignamos a esta proposición condicional es verdadero ya que
es razonable pensar que si no estudio no apruebo.
2) Consideremos que p es falsa y q es verdadera, y consideremos la proposición

condicional con los valores de verdad indicados:
Si no estudio, entonces aprobaré.

30
En este caso no se ve claro el determinar un único valor de verdad a la proposición ya

que hay quien diga que si me copio puedo aprobar sin necesidad de estudiar en cuyo
caso la proposición es verdadera, pero por otro lado, si no estudio no puedo aprobar
por lo que obtendría una proposición falsa. En la definición de verdad de esta
proposición veremos que se considera a la proposición como verdadera.
3) Consideremos que p es verdadera y q es falsa, y consideremos la proposición

Si estudio, entonces no aprobaré.

El valor de verdad que asignamos a esta proposición condicional es falso ya que nos
resulta razonable pensar que si estudio no apruebe.
4) Consideremos que p es verdadera y q es verdadera, y consideremos la proposición

Si estudio, entonces aprobaré.
El valor de verdad que asignamos a esta proposición condicional es verdadero ya que es
lógico pensar que si estudio apruebe.
Con este ejemplo observamos que no siempre concuerda con el lenguaje coloquial la
asignación del valor de verdad de una proposición en el contexto de la lógica.
En la siguiente tabla se resume el valor de verdad de la implicación entre dos

proposiciones.
Tabla de verdad (p )
p q P q
0 0 1
0 1 1
1 0 0
1 1 1
Para comprender el valor de verdad de la proposición condicional examinemos el

siguiente ejemplo.
Ejemplo 1.1.10
Consideremos las siguientes proposiciones:
p: Tengo dinero.
q: Voy al cine.
p q: Si tengo dinero, entonces voy al cine.
Asignemos valor de verdad a las proposiciones.

1) p es verdadera y q es verdadera.
La proposición p q es verdadera ya que se cumplió con ir al cine si se tenía dinero.
2) p es verdadera y q es falsa.

31
La proposición p q es falsa ya que no se cumplió con la promesa de ir al cine si se

tenía dinero.
3) p es falsa y q es verdadera.
La proposición p q es verdadera ya que cumplió la promesa aunque no se tenía
dinero, y por tanto no se dijo mentira.
4) p es falsa y q es falsa.
La proposición p q es verdadera ya que no se dijo ninguna mentira, no se tenía dinero

por tanto no se fue al cine.
En el lenguaje común, lo usual es que la hipótesis y la conclusión de una proposición

condicional tengan cierta relación; pero en lógica, no es necesario que la hipótesis y la
conclusión se refieran al mismo tema.
Ejemplos 1.1.11
a) p: 2<5.
q: Tengo clases de matemáticas.
p q: Si 2 < 5, entonces tengo clases de matemáticas.
b) p: 8 es par. verdadera
q: 2 es factor de 8. verdadera
p q: Si 8 es par, entonces 2 es factor de 8. verdadera
p q: 2 es factor de 8 si 8 es par.
p q: Una condición necesaria para que 8 sea par es que 2 sea factor de 8.
p q: Una condición suficiente para que 2 sea factor de 8 es que 8 sea par.
p q: 8 es par sólo si 2 es factor de 8.
p q: 8 es par en consecuencia 2 es factor de 8.
p q: 8 es par por lo tanto 2 es factor de 8.
p q: 8 es par luego 2 es factor de 8.
p q: 2 no es factor de 8 a menos que 8 sea par.
En este ejemplo se puede observar que la proposición condicional se puede escribir de

diferentes formas pero en esencia significan lo mismo.
c) s: Estudio. T: Tengo tiempo.

p q: Estudio sólo si tengo tiempo.
d) p =Juan es alto. q = Iremos a Roma.

p q Si Juan es alto entonces iremos a Roma.
Ejemplo 1.1.12
Escribe las siguientes proposiciones de la forma “Si p entonces q”.
a) María será una buena estudiante si estudia mucho.
Si maría estudia mucho, entonces será una buena estudiante.

32
b) Juan puede tomar cálculo sólo si ha aprobado el segundo o tercer grado de bachillerato.
Si Juan cursa cálculo, entonces tiene el nivel de segundo o tercer grado de bachillerato.
c) Cuando cantas, me duelen los oídos.

Si cantas, entonces me duelen los oídos.
d) Una condición necesaria para que el triángulo t sea equilátero es que t tenga iguales sus
tres ángulos.
Si el triángulo t es equilátero, entonces t tiene iguales sus tres ángulos.
e) Una condición suficiente para que la función f sea continua es que f sea diferenciable.
Si una función f es diferenciable, entonces f es continua.
f) No estoy en el bosque de Chapultepec a menos que esté en el museo del Papalote.

Si estoy en el museo del papalote, entonces estoy en el bosque de chapultepec.
Ejemplo 1.1.13
Supóngase que p es falsa (0), q es verdadera (1) y r es verdadera (1). Encontrar el valor
de verdad de cada una de las siguientes proposiciones.
a) ( p q ) r Verdadera
P q ( p q) (p q) r
1 0 0
b) p q r Verdadera
p r q r p q r
1 0 0 1
c) p (q r) Verdadera
q r p (q r)
1 1
Tipos de implicaciones
Es posible formar otras proposiciones condicionales a partir de la proposición

condicional p q, las cuales se definen a continuación.
Definición 1.1.12
Sean p y q dos proposiciones.
a) La implicación si no p, entonces no q, que se denota por p q es la proposición
inversa de la proposición condicional p q.

33
b) La implicación si q, entonces p, que se denota por q p, es la proposición recíproca de

la proposición condicional p q.
c) La implicación si no q, entonces no p, que se denota por q p es la proposición

contrarecíproca o contrapositiva de la proposición condicional p q.
Resumiendo
1) Implicación directa p q.
2) Implicación recíproca q p.
3) Implicación inversa p q.
4) Implicación contrarecíproca. q p.
A continuación mostramos el valor de verdad de estas proposiciones.
Implicación Implicación Implicaciópn Implicación

p q p q directa Inversa Recíproca Contrarecíproca
p q p q q p q p
0 0 1 1 1 1 1 1
0 1 1 0 1 0 0 1
1 0 0 1 0 1 1 0
1 1 0 0 1 1 1 1
Observe que la implicación y la contrapositiva tienen el mismo valor de verdad y la

inversa y recíproca también cumplen con esta propiedad.
Ejemplo 1.1.14
a) Escribir la proposición “Si 3>2, entonces 5<4” en forma simbólica.
b) Escribir la inversa, la recíproca y la contrarecírpoca de manera simbólica y con palabras.
c) Determine el valor de verdad de cada proposición.
Solución
a) Si definimos a p: 3>2, q: 5<4, podemos escribir la proposición de manera simbólica
como: p q.
b) Implicación inversa: p q : Si 3 2, entonces 5 4 o bien, si 3 no es mayor que 2,

entonces 5 no es menor que 4.
Implicación recíproca: q p: si 5<4, entonces 3>2.
Implicación contrarecírpoca: q p , Si 5 4, entonces 3 2.

34
c)
Implicación Inversa Recíproca Contrapositiva
p q p q p q p q q p q p
1 0 0 1 0 1 1 0
Definición 1.1.13 (Bicondicional)

Si p y q son proposiciones, la proposición compuesta p si y sólo si q, se llama
proposición bicondicional o doble implicación y se denota por p q.
Las palabras de enlace son:

p si y sólo si q.
p es una condición suficiente y necesaria para q.
La proposición bicondicional se puede interpretar como dos proposiciones

condicionales, siendo estas p q y q p.
En la siguiente tabla se resume el valor de verdad de la bicondicional.
Tabla de verdad (p q)
p q P q
0 0 1
0 1 0
1 0 0
1 1 1
Ejemplo 1.1.15
Sean p: T es un triángulo equilátero y
q: T es un triángulo con 3 lados iguales
La proposición bicondicional p q es:

T es un triángulo equilátero si y sólo si T es un triángulo con 3 lados iguales.
La proposición bicondicional q p es:

T es un triángulo con 3 lados iguales si y sólo si T es un triángulo equilátero.
Observe que las proposiciones bicondicionales tienen oraciones diferentes, sin embargo
lógicamente son iguales ya que de ambas se obtienen las mismas proposiciones condicionales
p q y q p. Así lógicamente no hay diferencia en considerar p q o q p.
Ejemplo 1.1.16
a) Sean a, b y c las longitudes de un triángulo rectángulo T siendo c la longitud del lado
mayor.

35
p: T es un triángulo rectángulo
q: a2 + b2 = c2
p q : T es un triángulo rectángulo si y sólo si a2+b2=c2.
O bien puede expresarse como:

p q : Una condición necesaria y suficiente para que un triángulo T sea rectángulo es
que sus lados satisfagan la relación a 2+ b2=c2 .
b) Sean p México es un país subdesarrollado y q México es un país de tercer mundo.

p q: México es un país subdesarrollado si y sólo si es un país del tercer mundo.
c) Sean p Se llenarán los pantanos y q Llueve de forma continua.

p q: Se llenarán los pantanos si y sólo si llueve de forma continua.
Ejemplo 1.1.17
Determine las proposiciones simples y simbolice los siguientes enunciados:
a) La división es un algoritmo y while es una instrucción de Pascal.
p=La división es un algoritmo. q=While es una instrucción de Pascal.
p q
b) El Basic es un lenguaje relacional o no es un lenguaje orientado a objetos.

p=El Basic es un lenguaje relacional.
q=Es un lenguaje orientado a objetos.
p q
c) Si Pedro no sabe lenguaje C entonces Laura compra un libro de C o escribe el programa

en Pascal.
p=Pedro sabe lenguaje C y q=Laura compra un libro de C.
r = Laura escribe el programa en Pascal
p q r
d) Si terminaste la tarea y te encuentras cansado, entonces no empieces a trabajar y

practica algún deporte.
p=Terminaste la tarea. q=Te encuentras cansado.

r=Empezar a trabajar. s=Practica algún deporte.
p q r s
e) Si hace frío o está húmedo el ambiente, y no te abrigas bien entonces no saldremos a

pasear.
p=Hace frío. q=Está húmedo el ambiente .
r=Te abrigas bien. s=Saldremos a pasear
p q r s

36
Para determinar el valor de verdad de cualquier proposición compuesta haremos uso de

las tablas de verdad. La tabla de verdad esta constituida por filas y columnas, las primeras
columnas de la tabla de verdad representan las proposiciones simples usadas en la proposición
compuesta y las filas representan los diferentes valores de verdad que pueden tomar las
proposiciones simples. Empezamos considerando el valor cero para cada proposición. El
número de filas queda determinado por el número n de proposiciones simples, siendo este 2 n.
Ejemplos 1.1.18
a) Construir la tabla de verdad de la proposición compuesta p q r p
Solución
Observe que la proposición está formada por tres proposiciones simples, p, q y r, por lo
que se debe considerar 2 3=8 filas.
p q r p q p r p
p q p q r p
0 0 0 0 1 1 0 0
0 0 1 0 1 1 1 1
0 1 0 0 1 1 0 0
0 1 1 0 1 1 1 1
1 0 0 0 1 0 0 0
1 0 1 0 1 0 0 0
1 1 0 1 0 0 0 1
1 1 1 1 0 0 0 1
b) Construir la tabla de verdad de r s t r

r s t r s t r r t r s t r
0 0 0 0 0 1 0
0 0 1 0 1 0 1
0 1 0 1 0 1 1
0 1 1 1 1 0 0
1 0 0 1 1 0 0
1 0 1 1 0 1 1
1 1 0 1 1 0 0
1 1 1 1 0 1 1
c) Construir la tabla de verdad de la siguiente proposición p q r

p q r p q p q r
0 0 0 1 0
0 0 1 1 1
0 1 0 1 0
0 1 1 1 1
1 0 0 0 1
1 0 1 0 0
1 1 0 1 0

37
1 1 1 1 1
1.1.3 Tautologías, contradicciones y contingencias
Definición 1.1.14 (Tautología)

Sea p una proposición compuesta formada por las proposiciones simples p1, p2, p3, . . . ,
pn. La proposición p es una tautología, si p es verdadera para todos los valores de verdad que
se asignen a p1, p2, p3, . . . , p n. Denotaremos una tautología con To.
Ejemplo 1.1.19
a) La proposición más simple que es una tautología es p p
p p p p
0 1 1
1 0 1
b) Construir la tabla de verdad de la proposición: p q p q
P q a q p q B a b
p q p q
0 0 1 1 0 1 1
0 1 1 0 0 1 1
1 0 0 1 1 0 1
1 1 1 0 0 1 1
Como los valores de verdad de la proposición son verdaderos, entonces decimos que la
proposición es una tautología.
Definición 1.1.15 (Contradicción)

pn. La proposición p es una contradicción, si p es falsa para todos los valores de verdad que se
asignen a p1, p2, p3 , . . . , p n. Denotaremos una contradicción con Fo.
Ejemplo 1.1.20
a) La proposición más simple que es una contradicción es p p

38
p p p p
0 1 0
1 0 0
b) Construir la tabla de verdad de la proposición p q p q p q p q
P q p q a b c d
p q p q p q p q m=a b n=c d m n
0 0 1 1 0 1 1 1 0 1 0
0 1 1 0 1 1 0 0 1 0 0
1 0 0 1 1 0 1 0 0 0 0
1 1 0 0 1 1 1 0 1 0 0
Como los valores de verdad de la proposición son falsos, entonces decimos que la
proposición es una contradicción.
c) Construir la tabla de verdad de la proposición: p q p q

P Q a p p q b a b
p q p q
0 0 1 1 1 0 0
0 1 1 1 1 0 0
1 0 0 0 0 1 0
1 1 1 0 1 0 0
En este caso también se tiene que la proposición es una contradicción.
Definición 1.1.16 (Contingencia)

pn. La proposición p es una contingencia si es cierta en algunos casos y falsa en otros,
dependiendo del valor de verdad de las proposiciones p1, p2, p3, . . . , pn.
Ejemplos 1.1.21
a) Las proposiciones más simples que son contingencias son las proposiciones: p q ,
p q, p q, p q y p q.
b) Construir la tabla de verdad de la proposición p p r q r

p Q r a b a b c p c

39
p r q r a b
0 0 0 1 1 1 0 1
0 0 1 1 1 1 0 1
0 1 0 1 0 0 1 0
0 1 1 1 1 1 0 1
1 0 0 0 1 0 1 1
1 0 1 1 1 1 0 0
1 1 0 0 0 0 1 1
1 1 1 1 1 1 0 0
Como los valores de verdad de la proposición son algunos falsos y otros verdaderos,
entonces decimos que la proposición es una contradicción.
Ejemplo 1.1.22
Determinar si las siguientes proposiciones son tautologías, contingencias o
contradicciones:
a) p q r p q r Tautología
P Q r a b r c b c
p q a r a r
0 0 0 0 0 1 1 1
0 0 1 0 0 0 0 1
0 1 0 0 0 1 1 1
0 1 1 0 0 0 0 1
1 0 0 0 0 1 1 1
1 0 1 0 0 0 0 1
1 1 0 1 0 1 1 1
1 1 1 1 1 0 1 1
b) p q r p q p r Contradicción
P q r a a b q c r d e b e
q r p a p q p r c d b e
0 0 0 0 1 0 1 0 1 0 0 1 0
0 0 1 1 0 0 1 0 0 0 0 1 0
0 1 0 1 0 0 0 0 1 0 0 1 0
0 1 1 1 0 0 0 0 0 0 0 1 0
1 0 0 0 1 1 1 1 1 1 1 1 0
1 0 1 1 0 0 1 1 0 0 1 1 0
1 1 0 1 0 0 0 0 1 1 1 1 0
1 1 1 1 0 0 0 0 0 0 0 1 0

40
c) p q q p Contingencia
p Q a b a b
p q q p
0 0 1 1 1
0 1 1 0 0
1 0 0 1 0
1 1 1 1 1
d) p q p r q r Tautología
p q r a b c d c d
p q p r a b q r
0 0 0 1 0 0 0 1
0 0 1 1 0 0 0 1
0 1 0 0 0 0 0 1
0 1 1 0 0 0 1 1
1 0 0 0 0 0 0 1
1 0 1 0 1 0 0 1
1 1 0 1 0 0 0 1
1 1 1 1 1 1 1 1
e) p q q p Tautología
p q a b a b
p q q p
0 0 0 0 1
0 1 0 1 1
1 0 0 1 1
1 1 1 1 1

41
1.1.4 Equivalencias lógicas
En algunos casos, es posible que dos proposiciones tengan los mismos valores de
verdad, sin importar los valores de verdad de las proposiciones simples que las constituyen.
Cuando esto sucede se dice que las proposiciones son lógicamente equivalentes.
Definición 1.1.17 (Lógicamente equivalentes)

Las proposiciones compuestas p=p(p1, p2, p3, ... p n) y q=q(p1, p2, p3, ... ,p n) son
lógicamente equivalentes y se escribe p q o bien p q, siempre que dados cualesquiera
valores de vedad de p1, p2 , ,..., p n, p y q son ambas verdaderas o falsas.
Otra forma de expresar esta definición es:

Las proposiciones p=p(p1, p2, p3, . . . , p n) y q=q(p1, p2, p3, . . . , p n) son lógicamente
equivalentes, si ambas tienen tablas de verdad idénticas.
Nota 1.1.4: En este libro usaremos la notación p q, para indicar que las proposiciones p y q
son lógicamente equivalentes.
Observación: p q se cumple precisamente cuando p(p1, p2, p3, ... , p n) q(p1, p2, p3, ... , p n) es
una tautología.
Ejemplo 1.1.23
Demuestre que las proposiciones p q y p q son lógicamente equivalentes.
Solución
Para determinar la equivalencia de las proposiciones haremos las tablas de verdad de
cada una de ellas.
p Q p q p q p q p q p q
0 0 0 1 0 0 1 1 1
0 1 1 0 0 1 1 0 0
1 0 1 0 1 0 0 1 0
1 1 1 0 1 1 0 0 0

42
Como los valores de verdad de las proposiciones son iguales decimos que son
lógicamente equivalentes.
1.1.5 Álgebra de proposiciones
Por medio de la verificación de proposiciones equivalentes usando tablas de verdad, es

posible determinar algunas propiedades que cumplen las proposiciones, en particular, las
propiedades principales se presentan como las leyes del álgebra de proposiciones, las cuales se
dan a continuación.
Leyes del álgebra de proposiciones
Leyes idempotentes 5b.- p To p

1a.- p p p
1b.- p p p
Leyes de dominación
Leyes asociativas 6a.- p Fo Fo
2a.- (p q) r p (q r) 6b.- p To To
2b.- (p q) r p (q r)
Leyes inversas
7a.- p p To
Leyes conmutativas
7b.- p p Fo
3a.- p q q p
3b.- p q q p Leyes de complementación
8a.- p p
Leyes distributivas 8b.- Fo To
4a.- p (q r) (p q) (p r) 8.c.- To Fo
4b.- p (q r) (p q) (p r)
Leyes de De Morgan
9a.- p q p q
9b.- p q p q
Leyes de identidad
5a.- p Fo p

43
Leyes de absorción
10a.- p (p q) p
10b.- p (p q) p
Equivalencia para la condicional

p q p q
Equivalencia para la bicondicional

p q p q q p

23
Unidad II: Teoría de Conjuntos Álgebra de conjuntos
Recordemos que To representa una proposición que es una tautología y que Fo representa a
una proposición que es una contradicción.
Con el uso de estas leyes es posible la simplificación de proposiciones compuestas

complejas.
Para las proposiciones primitivas p, q ¿existe una forma más sencilla de expresar la
proposición compuesta (p q) p q ? es decir podemos encontrar una expresión más sencilla
que sea lógicamente equivalente a la dada?.
Ejemplo 1.24
Usando el álgebra de proposiciones demuestre que las siguientes proposiciones son
lógicamente equivalentes.
a) (p q) p q p
p q p q D’ Morgan
p q p q Complemento
p q q Distributiva
p Fo Inversa
p Identidad
b) [(q (r r ) (q r)] q r
q To q r Inversa
q q r Identidad
q q q r Distributiva
To q r Inversa
q r Identidad
c) [(p q) (r p)] To
p q r p Equivalencia de la implicación
p p r q Asociativa
To r q Inversa
To Dominación
d) (p q r) (p q r ) To
((p q) r) ((p q) r ) Asociativa
((p q) r) p q r D’ Morgan
m r m r Cambio de variable
m r m r D’ Morgan

88
s s Cambio de variable
To Inversa
e) (p q ) (p r) (p q) p
((p q ) (p r)) (p q) Asociativa
(p (q r)) (p q) Distributiva
(p m) (p q) Cambio de variable
p (m q) Distributiva
p q r q Sustitución de variable
p q q r Conmutativa
p To r Inversa
p To Dominación
p Identidad
f) (p q) p q p
p q p q D’ Morgan
p q p q Complemento
p q q Distributiva
p Fo Inversa
p Identidad
Ejemplo 1.1.25
Usando el álgebra de proposiciones simplifique, a su mínima expresión, las proposiciones
dadas.
a) (p q) p
p (p q) Conmutativa
( p p) ( p q) Distributiva
Fo ( p q) Inversa
p q Identidad
b) [p ( p q)] [q (q r)] q
[(p p ) (p q)] [q (q r)] q Distributiva
[Fo (p q)] [q (q r)] q Inversa
(p q) [q (q r)] q Identidad
(p q) [q m] q cambio de variable
(p q) q Asociativa
q Absorción

89
Ejemplo 1.1.26
Demostrar que se cumplen las leyes de idempotencia
a) p p p.
Solución
Para demostrar que esta ley se cumple podemos partir de cualquier lado de la identidad y
aplicando las leyes del álgebra de proposiciones podemos llegar al otro lado de la identidad.
Partiendo del lado derecho de la identidad se tiene

p p To Identidad
p p (p p ) Inversa
p (p p) (p p ) Distributiva
p (p p) Fo Inversa
p p p Identidad
Partiendo del lado izquierdo de la identidad se tiene:

p p (p p) Fo Identidad
p p (p p) (p p ) Inversa
p p p (p p ) Distributiva
p p p To Inversa
p p p Identidad
b) p p p
Partiendo del lado derecho de la identidad se tiene
p p Fo Identidad
p p (p p ) Inversa
p (p p)(p p ) Distributiva
p (p p) To Inversa
p p p Identidad
Partiendo del lado izquierdo de la identidad se tiene:

p p (p p) To Identidad
p p (p p) (p p ) Inversa
p p p (p p ) Distributiva
p p p Fo Inversa
p p p Identidad
Ejemplo 1.1.27
Demostrar que se cumple la ley de absorción p (p q) p.
Solución
p (p q) (p To) (p q) Identidad

90
p (To q) Distributiva
p To Dominación
p Identidad
1.2 INFERENCIA LOGICA
1.2.1 Definiciones básicas
Definición 1.2.1 (Inferencia)

La inferencia es una actividad en la que se afirma una proposición sobre la base de otra u
otras proposiciones aceptadas como el punto de partida del proceso.
A cada inferencia posible le corresponde un argumento (o razonamiento), y de estos

argumentos trata la lógica primordialmente.
Uno de los problemas frecuentes es demostrar que una proposición se cumple, en

particular, en matemáticas, demostrar teoremas; ¿Cómo realizar las demostraciones de los
teoremas?
Con frecuencia los teoremas son de la forma
Si p, entonces q (1)
Una demostración de (1) es un razonamiento que prueba que (1) es verdadera.
Recordemos la tabla de verdad de la implicación
Tabla de verdad
p q p q
1 1 1
1 0 0
0 1 1
0 0 1
Si p es falsa, la expresión (1) es verdadera; por ello, sólo se necesita considerar el caso en el
cual p es verdadera.
En la realización de una demostración debe existir certeza de que los razonamientos

utilizados son válidos.
Ejemplo 1.2.1
Considere la siguiente sucesión de proposiciones.
El celular está sobre el escritorio o en mi portafolio.
El celular no está sobre el escritorio. (2)

91
Suponiendo que estos enunciados son verdaderos es razonable concluir que

El celular está en mi portafolio . (3)
El proceso de obtener una conclusión a partir de una sucesión de proposiciones se

denomina razonamiento deductivo. Las proposiciones dadas en (2) se llaman hipótesis o
premisas (proposiciones que se consideran verdaderas) y la proposición que sigue a las hipótesis
(3) se llama conclusión.
Cualquier razonamiento tiene la forma de una implicación expresada de la siguiente

manera:
Si p1 y p2 y ... y p n, entonces q (4)
Se dice que el razonamiento (4) es válido si la conclusión es consecuencia de las hipótesis;

es decir, si p1 y p2 y...y p n, son todas verdaderas entonces q también lo es.
En otras palabras un razonamiento es válido si p1 y p2 y...y p n implican lógicamente a q.
Definición 1.2.2 (Implicación lógica)

La proposición compuesta p=p(p1, p2, ... , pn) implica lógicamente la proposición
compuesta q=q(p1, p2, ... , p n), en símbolos p q, siempre que dados cualesquiera valores de
verdad para p1, p2 , ... , p n , si p es verdadera q también lo es.
Observación: p( p1, p2, ... , p n) q(p1, p2, ... , p n), se cumple precisamente cuando p(p1, p2, ... ,
pn) q(p1, p2, ... , p n) es una tautología.
Definición 1.2.3 (Razonamiento o argumento)

Un razonamiento es una secesión de proposiciones escritas de la manera siguiente:
p1
p2
p3
.
.
pn
Las proposiciones p1, p2, p3, … , pn reciben el nombre de hipótesis o premisas, el símbolo
se lee “por lo tanto” o bien “en consecuencia”, y la proposición q se conoce como conclusión.
El razonamiento es válido si siempre que p1 p2 ... p n es verdadera, entonces q también lo

es. Pero p1 p2 ... pn es verdadera cuando pi es verdadera para i=1,2,...,n.

92
Otra característica de un razonamiento válido es que la proposición:

(p1 p2 ... p n q) es una tautología.
Una forma de demostrar la validez de un razonamiento es usando la tabla de verdad.
Ejemplo 1.2.2
Determine si la conclusión C se obtiene lógicamente de las premisas H 1 y H2 .
a) H1: p q H2: p C: q
H2 C H1
p Q p q
0 0 1
0 1 1
1 0 0
1 1 1
Observe que sólo en un caso las dos premisas son verdaderas y en este la conclusión
también lo es, por lo tanto el argumento es válido.
b) H1: p q H2: p C: q
p C H2 H1
q p p q
0 0 1 1
0 1 1 1
1 0 0 0
1 1 0 1
Observe los primeros dos renglones de la tabla, en estos se tienen premisas verdaderas, sin
embargo, en el primer renglón se tiene conclusión falsa y en el segundo conclusión verdadera.
Como no siempre que se tienen premisas verdaderas se obtiene una conclusión verdadera
entonces el argumento no es válido. Esto es, la conclusión no es una consecuencia lógica de las
premisas.
Ejemplo 1.2.3
Represente simbólicamente el razonamiento siguiente
Si 2 = 3, entonces 2 < 5.
2 < 5.
2=3
y determine la validez del razonamiento.
Solución

93
p : 2=3
q : 2<5

94
Razonamiento
P1: p q
P2: q
C p
Construimos la tabla de verdad.
C P2 P1
P q p q
1 1 1
1 0 0
0 1 1
0 0 1
Recordemos que un razonamiento es válido si siempre que P 1 y P2 sean verdaderas,

entonces C también es verdadera.
Observemos las filas 1 y 3, en estas filas se cumple que P 1 y P2 son verdaderas pero la
conclusión es verdadera en el primer renglón y falsa en el tercer renglón, por lo tanto, este
razonamiento no es válido.
Seguir con el proceso de elaborar la tabla de verdad para determinar si un razonamiento es

correcto o no, se puede complicar cuando se tienen muchas hipótesis. Por ello es conveniente
utilizar otros métodos de demostración.
Otra forma de mostrar la validez de un razonamiento es analizando sus premisas.
Ejemplo 1.2.4
Resolver el inciso a) del ejemplo 1.2.2 analizando sus premisas.
Como las premisas son proposiciones que se consideran verdaderas, en este caso se tiene
que, H1: p q y H2: p son verdaderas, si H2 es verdadera se tiene que p es una proposición
verdadera, dado que la implicación p q es verdadera y p es verdadera se tiene que q también es
verdadera, ya que si fuera falsa entonces la implicación sería falsa y estamos suponiendo que la
implicación es verdadera. Por lo tanto la conclusión C: q, se obtiene lógicamente de las premisas
H 1 y H 2.
Para demostrar la validez de un argumento analizando las premisas se siguen las siguientes
reglas de inferencia.

95
1.2.2 Leyes de inferencia
La demostración de las siguientes leyes se hace usando la tabla de verdad.
En cada ley, los primeros renglones representan las premisas, los tres puntos significan “por
lo tanto” o bien “en consecuencia” y el último renglón representa la conclusión.
Leyes de inferencia
1. Modus Ponendo Ponens (MPP): “Método de afirmación”

p
p q
q
[(p q) p] q es una tautología.
Ejemplo 1.2.5
Si Lidia Gana el melate, entonces Pedro renuncia a su trabajo
Lidia Ganó el melate.
Por lo tanto, Pedro renuncia a su trabajo.
2. Modus Tollendo Tollens (MTT): “ Método de negación”

p q
q
p
[(p q) q ] p Es una tautología.
Ejemplo 1.2.6
Si Toño es elegido Jefe del departamento de Matemáticas, entonces José será coordinador
de asignatura.
José no es coordinador de asignatura.
Por lo tanto, Toño no es elegido Jefe del departamento de Matemáticas.
3. Modus Tollendo Ponens (MTP) “Método que negando afirma”.

Silogismo disyuntivo (SD)
p q p q
p q

96
q p
Ejemplo 1.2.7
La calculadora de Sofía está sobre el escritorio o en mi portafolio.
La calculadora de Sofía no está sobre el escritorio.
Por lo tanto, la calculadora de Sofía está en mi portafolio.
4. Silogismo Hipotético (SH).

p q
q r
p r
Ejemplo 1.2.8
Si Juan aprueba cuatro materias, entonces podrá inscribirse.
Si Juan puede inscribirse, entonces se irá de vacaciones.
Por lo tanto, Si Juan aprueba cuatro materias, se irá de vacaciones.
5. Conjunción
p
q

97
p q
Ejemplo 1.2.9
Pedro estudió matemáticas discretas.
Pedro aprobó la materia de matemáticas discretas.
Por lo tanto, Pedro estudió y aprobó la materia de matemáticas discretas.
6. Simplificación Conjuntiva
p q
p
q
Ejemplo 1.2.10
El basic es un lenguaje de programación y el windows es un sistema operativo.
Por lo tanto, el basic es un lenguaje de programación.
El windows es un sistema operativo.
7. Ley de Adición o Amplificación disyuntiva

p
p s
p m
Ejemplo 1.2.11

98
Los niños son traviesos.
Por lo tanto, los niños son traviesos o inteligentes.
Los niños son traviesos o inquietos.
8. Ley de casos
p r
q r
(p q) r
Ejemplo: 1.2.12
Si el día está soleado entonces juego fútbol.
Si es fin de semana, juego fútbol.
Por lo tanto, si el día está soleado o es fin de semana, entonces juego fútbol.
1.2.3 Demostración de argumentos
Para demostrar la validez de un argumento se siguen las siguientes reglas de inferencia.
Reglas de inferencia
Regla P: Una premisa puede introducirse en cualquier punto de la demostración.
Regla T: Una proposición s puede introducirse si es lógicamente equivalente o bien, es implicada

lógicamente, por alguna o algunas proposiciones precedentes en la demostración.
Regla CP: (Regla de prueba condicional) Si se puede concluir que s es verdadera a partir de r y
de un conjunto de premisas, entonces se puede concluir, r s, a partir sólo del
conjunto de premisas.
En general la regla CP se usa si la conclusión es de la forma r s, en tales casos r se
toma como una premisa adicional y s se deduce de las premisas dadas y de r.
Hay varias formas de demostración, en este libro manejaremos la demostración directa y la

demostración por contradicción o reducción al absurdo.

99
Una demostración directa supone que las premisas son verdaderas y después, usando tanto
estas premisas, así como axiomas, definiciones y teoremas establecidos con anterioridad, se
prueba directamente que la conclusión es verdadera.
Ejemplo 1.2.13
a) Demuestre que r es una deducción válida de las premisas p q, q r y p.
Pasos Razones
(1) p Regla P
(2) p q Regla P
(3) q Regla T, (1) (2) Modus Ponens
(4) q r Regla P
(5) r Regla T, (3) (4) Modus Ponens
b) Pruebe que p se obtiene de q, p→q.

Pasos Razones
(1) p→q Premisa
(2) p→ p Regla T (1) Equivalencia
(3) q Premisa
(4) p Regla T (2) (3) Modus Ponens
c) Muestre que r (p q) es una conclusión válida de las premisas p q, q r, p my m.

Pasos Razones
(1) m Premisa.
(2) p m Premisa.
(3) p Regla T (1) (2) Modus Tollens.
(4) p q Premisa.
(5) q Regla T (3) (4) Silogismo Disyuntivo.
(6) q r Premisa.
(7) r Regla T (5) (6) Modus Ponens.
(8) r (p q) Regla T (7) (4) Amplificación Conjuntiva.
d) Pruebe que r s se obtiene lógicamente de las premisas

c d, (c d) h , h (a b ) y (a b ) (r s)
Pasos Razones
(1) c d Regla P.
(2) (c d) h Regla P.
(3) h Regla T, (1)(2) Modus Ponens.
(4) h (a b) Regla P.
(5) (a b ) Regla T, (3)(4) Modus Ponens.
(6) (a b ) (r s) Regla P.
(7) (r s) Regla T (5)(6) Modus Ponens.

100
Otra forma:
Pasos Razones
(1) (c d) h Regla P.
(2) h (a b) Regla P.
(3) (c d) (a b ) Regla T, (1)(2) Silogismo Hipotético.
(4) (a b ) (r s) Regla P.
(5) (c d) (r s) Regla T, (3)(4) Silogismo Hipotético.
(6) (c d) Regla P.
(7) r s Regla T (5)(6) Modus Ponens.
e) Pruebe que s r está implícita tautológicamente en (p q) (p r) (q s).

Esto es, tenemos 3 premisas.
Pasos Razones
(1) p q Premisa.
(2) p q Regla T (1) Equivalencia.
(3) p q Regla T (2) Equivalencia.
(4) q s Premisa.
(5) p s Regla T (3) (4) Silogismo Hipotético.
(6) s p Regla T (5) Equivalencia.
(7) s p Regla T (6) Equivalencia.
(8) p r Premisa.
(9) s r Regla T (7) (8) Silogismo Hipotético.
(10) s r Regla T (9) Equivalencia.
(11) s r Regla T (10) Equivalencia.
f) Muestre que r→s puede deducirse de las premisas p→(q→s), r p y q.

Como la conclusión es una condicional se incluirá r como premisa adicional y se concluirá
sólo s.
Pasos Razones
(1) r Premisa.
(2) r p Premisa.
(3) p Regla T (1) (2) Silogismo Disyuntivo.
(4) p→(q→s) Premisa.
(5) q→ s Regla T (3) (4) Modus Ponens.
(6) q Premisa.
(7) s Regla T (5) (6) Modus Ponens.
(8) r→s Regla CP.
Ejemplo 1.2.14
Determinar si los siguientes argumentos son válidos.
a)

101
p r
p q
q s
r s
Pasos Razones
(1) p q Premisa.
(2) q s Premisa.
(4) p r Premisa.
(5) r Premisa Adicional.
(6) p Regla T (4) (5) Modus Tollens.
(7) s Regla T (3) (6) Modus Ponens.
b)
q s
p q
p s p r
r t
p t
Pasos Razones
(1) q s Premisa.
(2) p q Premisa.
(4) p s p r Premisa.
(5) p r Regla T (3) (4) Modus Ponens.
(6) r t Premisa.
(7) p t Regla T (5) (6) Silogismo Hipotético.
c)
s r
p
p q r
s
Pasos Razones
(1) p Premisa.
(2) p q r Premisa.

102
(3) q r Regla T (1) (2) Modus Ponens.

(4) r Regla T (3) Simplificación Conjuntiva.
(5) s r Premisa.
(6) s Regla T (4) (5) Modus Tollens.
Ejemplo 1.2.15
Simbolice los enunciados dados y muestre que constituyen un argumento válido.
a) O aumentaron los impuestos o si aumentan los gastos se eleva la deuda. Si los impuestos
aumentaron entonces el costo de recaudar los impuestos crece. Si un aumento en los gastos
implica que el gobierno pide prestado más dinero, entonces si se eleva la deuda aumentan
las tasas de interés. Si no se aumentan los impuestos y el costo de recaudación de impuestos
no crece, entonces si la deuda se eleva entonces el gobierno pide prestado más dinero. El
costo de recaudación de impuestos no crece. O las tasas de interés no aumentan o el
gobierno no pide prestado más dinero. Por lo tanto, o la deuda no se eleva o los gastos no
aumentan.
Solución
p: Aumentan los impuestos.
q: Aumentan los gastos.
r: Se eleva la deuda.
s: El costo de recaudar impuestos crece.
t: El gobierno pide prestado más dinero.
u: Aumentan las tasas de interés.
Premisas: p (q r)
p s
(q t) (r u)
( p s ) (r t)
s
u t
Conclusión: r q
Pasos Razones
(1) s Premisa.
(2) p s Premisa.
(3) p Regla T, (1) (2) Modus tollens.
(4) p s Regla T, (1) (3) Equivalencia.
(5) ( p s ) (r t) Premisa.
(6) r t Regla T, (4) (5) Modus ponens.
(7) p (q r) Premisa.
(8) q r Regla T, (3) (7) Silogismo disyuntivo.
(9) q t Regla T, (6) (8) Silogismo hipotético.
(10) (q t) (r u) Premisa.
(11) r u Regla T, (9) (10) Modus ponens.

103
(12) u t Premisa.
(13) u t Regla T, (12) Equivalencia.
(14) r t Regla T, (11) (13) Silogismo hipotético.
(15) t q Regla T, (14) Equivalencia.
(16) r q Regla T, (11) (13) Silogismo hipotético.
(17) r q Regla T, (16) Equivalencia.
b) O Pedro asistió a la fiesta o Pedro no fue invitado a la fiesta. Si sus amigos deseaban la
presencia de Pedro en la fiesta entonces Pedro fue invitado a la fiesta. Pedro no asistió a la
fiesta. Si los amigos no deseaban la presencia de Pedro en la fiesta y Pedro no fue invitado
a la fiesta, entonces Pedro se va de la fiesta. Por lo tanto, Pedro se va de la fiesta.
Solución
p: Pedro asistió a la fiesta.
q: Pedro fue invitado a la fiesta.
r: Los amigos deseaban la presencia de Pedro en la fiesta.
s: Pedro se va de fiesta.
Premisas: p q
r q
p
(r q) s
Conclusión: s
Pasos Razones
(1) p Premisa.
(2) p q Premisa.
(3) q Regla T, (1) (2) Silogismo Disyuntivo.
(4) r q Premisa.
(5) r Regla T, (3) (4) Modus Tollens.

(6) r q Regla T, (3) (5) Amplificación Conjuntiva.
(7) (r q) s Premisa.
(8) s Regla T, (6) (7) Modus Ponens
c) Si se desarrolla una escasez de artículos de consumo hay alza de precios. Si hay un cambio
en el gobierno no seguirán los controles fiscales. Si la amenaza de inflación persiste
seguirán los controles fiscales. Si hay sobreproducción no hay alza de precios. O hay
sobreproducción o hay un cambio de gobierno. Por lo tanto, o no se desarrolla una escasez
de artículos de consumo o la amenaza de inflación no persiste.
Solución
p: Se desarrolla una escasez de artículos de consumo.

104
q: Hay alza de precios.

r: Hay un cambio en el gobierno.
s: Seguirán los controles fiscales.
t: La amenaza de inflación persiste.
u: Hay sobreproducción.
Premisas: p q
r s
t s
u q
u r
Conclusión: p t
Pasos Razones
(1) p q Premisa.
(2) u q Premisa.
(3) q u Regla T, (2) Equivalencia.
(4) p u Regla T, (1) (3) Silogismo Hipotético.
(5) u r Premisa.
(6) u r Regla T, (5) Equivalencia.
(7) p r Regla T, (4) (6) Silogismo Hipotético.
(8) r s Premisa.
(9) p s Regla T, (7) (8) Silogismo Hipotético.
(10) t s Premisa.
(11) s t Regla T, (10) Equivalencia.
(12) p t Regla T, (9) (11) Silogismo Hipotético.
(13) p t Regla T, (12) Equivalencia.
d) Si trabajo gano dinero, pero si estoy de ocioso gozo la vida. O trabajo o estoy de ocioso.
Sin embargo, si trabajo no gozo la vida mientras que si estoy de ocioso no gano dinero. Por
lo tanto, gozo la vida si y sólo si no gano dinero.
Solución
p: Trabajo.
q: Gano dinero.
r: Estoy de ocioso.
s: Gozo la vida.
Premisas: (p q) (r s)
p r
(p s ) (r q )
Conclusión: s q (s q ) ( q s)

105
Pasos Razones
(1) (p q) (r s) Premisa.
(2) p q Regla T, (1) Simplificación Conjuntiva.
(3) r s Regla T, (1) Simplificación Conjuntiva.
(4) (p s ) (r q ) Premisa.
(5) p s Regla T, (4) Simplificación Conjuntiva.
(6) r q Regla T, (4) Simplificación Conjuntiva.
(7) s p Regla T, (5) Equivalencia.
(8) p r Premisa.
(9) p r Regla T, (8) Equivalencia.
(10) s r Regla T, (7) (9) Silogismo Hipotético.
(11) s q Regla T, (6) (10) Silogismo Hipotético.
(12) q p Regla T, (2) Equivalencia.

(13) q r Regla T, (9) (12) Silogismo Hipotético.
(14) q s Regla T, (3) (13) Silogismo Hipotético.
(15) (s q ) ( q s) Regla T, (14) Amplificación conjuntiva.
(16) s q Regla T, (15) Equivalencia.
e) Andrés está jugando fútbol. Si Andrés está jugando fútbol, entonces no está estudiando. Si
Andrés no está estudiando, entonces su padre no le prestará el carro. Por lo tanto el padre
de Andrés no le prestará el carro.
Solución:
p: Andrés está jugando fútbol.
q: Andrés está estudiando.
r: Su papá le prestará el carro.
Premisas: p
p q
q r
Conclusión: r
Pasos Razones
(1) p q Premisa.
(2) q r Premisa.
(3) p r Regla T (1) (2) Silogismo Hipotético.
(4) p Premisa.
5) r Regla T (3) (4) Modus Ponens.

106
f) Si el payaso no pudiera estar en la fiesta o los bocadillos no llegaran a tiempo, entonces la

fiesta de cumpleaños tendría que cancelarse y Paty se enojaría. Si la fiesta se cancelara
habría que devolver el dinero. No se devolvió el dinero. Por lo tanto el payaso pudo estar en
la fiesta.
Solución:
p: El payaso pudo estar en la fiesta.
q: Los bocadillos llegan a tiempo.
r: La fiesta de cumpleaños tendría que cancelarse.
s: Paty se enojaría.
t: Se devolvería el dinero.
Premisas: p q r s
r t
t
Conclusión: p
Pasos Razones
(1) r t Premisa.
(2) t Premisa.
(3) r Regla T (1) (2) Modus Tollens.
(4) r s Regla T (3) Amplificación Disyuntiva.
(5) r s Regla T (4) Equivalencia De Morgan.
(6) p q r s Premisa.
(7) p q Regla T (5) (6) Modus Tollens.
(8) p q Regla T (7) Equivalencia De Morgan.
(9) p Regla T (8) Simplificación Conjuntiva.
1.4 FUNCIONES LÓGICAS Y CUANTIFICADORES
1.3.1 Funciones lógicas y conjunto de validez
Empecemos por considerar las proposiciones siguientes:
a) Este año no es bisiesto.

b) El Tigris es un río.
c) Juan es soltero.
Cada proposición se puede dividir en dos partes, la primera parte es el sujeto:

“este año”, “el Tigris” y “Juan”

107
y la segunda parte es el predicado:

“no es bisiesto”, “es un río” y “es soltero”
de cada proposición respectivamente.
Definición 1.3.1 (Sujeto de una oración)

El sujeto de una oración son personas, animales, ciudades, etc. a las cuales pueden
asignarse atributos.
Definición 1.3.2 (Predicado de una oración)

El predicado es una determinada propiedad o atributo referido al sujeto, designado por
adjetivos, nombres, adverbios y verbos.
Podemos tener las siguientes propiedades en donde se usa la misma palabra como verbo,
adjetivo y adverbio.
a) Elena es un encanto.
b) Elena encanta.
c) Elena es encantadora.
Notación: Al sujeto lo denotaremos con letras minúsculas como con las que acostumbramos
denotar a las variables en cálculo y al predicado con letras mayúsculas.
Sujetos Predicados
j=Juan S=soltero
p=Pedro
l=Luis
t=Tigris R=Río
En particular podemos formar tres proposiciones diferentes con el mismo predicado, estas
son:
Juan es soltero.
Pedro es soltero.
Luis es soltero.
Observamos que en estas tres proposiciones el sujeto varia y el predicado está fijo, De esta
manera es posible considerar al sujeto como una variable, de modo que, se puede considerar a las
tres proposiciones con un solo enunciado de la siguiente forma:
x es soltero
donde el papel de x lo representan: Juan, Pedro y Luis.
Si el sujeto está constituido de un solo elemento se le llama variable individual.

108
Definición 1.3.3 (función lógica o función proposicional)

Una función lógica o función proposicional, P(x) simple, de una variable, es una
expresión que consiste de una variable individual x, y de un predicado.
Ejemplo 1.3.1
a) x tiene cabello oscuro.
b) P(x)=x es un entero impar.
c) Q(x): x2 + 2x es un entero par
d) R(x): x2–x–6=0
Consideremos las funciones proposicionales:
A(x)=x es apuesto y S(x)=x es soltero.
Usando los conectivos lógicos podemos unir estas funciones lógicas simples, para formar
funciones lógicas compuestas, como por ejemplo:
a) x es apuesto y x es soltero.
b) x es apuesto o x es soltero.
c) Si x es apuesto entonces x es soltero.
Ejemplo 1.3.2
Sean P(x)=x es un gato y Q(x)=x tiene cola.
P(x) Q(x)= x es un gato y x tiene cola
P(x) Q(x)= Si x es un gato entonces x tiene cola.
En particular si se considera una variable diferente para cada función es posible tener
funciones lógicas de dos variables.
Ejemplo 1.3.3
a) Sean A(x)=x es apuesto y S(y)=y es soltero.
Podemos obtener funciones de dos variables como las siguientes:
P(x,y)=A(x) S(y)=x es apuesto y y es soltero.
Q(x, y)=A(x) S(y)=Si x es apuesto entonces y es soltero.
b) Sean P(x)=x es un gato y Q(y)=y tiene cola.

M(x,y)=P(x) Q(y)= x es un gato y y tiene cola.
N(x,y)=P(x) Q(x)= Si x es un gato entonces y tiene cola.
c) Sean R(x)=x es un planeta y S(y):y es una estrella.

B(x,y)=R(x) S(y)=x es un planeta y y es una estrella.

109
B(x,y)=R(x) S(y)=Si x es un planeta entonces y es una estrella.

B(x,y)=R(x) S(y)=x es una planeta o y es una estrella.
También es posible formar funciones lógicas de dos o más variables en las que se tiene un
solo predicado, algunos ejemplos de estos se presentan a continuación:
Ejemplos 1.3.4
a) M(x,y)=x es mayor que y.
Si tanto x como y se reemplazan por valores se obtiene una proposición.
Suponga que x=3yy=4.
M(3,4)=3 es mayor que 4. Proposición falsa.
Suponga que x=6 y y=4.
M(6,4)=6 es mayor que 4. Proposición verdadera.
b) H(x,y)=x es hermano de y.
H(maría, Ana) = María y Ana son hermanas.
c) U(x,y,z)=x está entre y y z.

U(1,2,3) = 1 está entre 2 y 3. Proposición falsa.
U(2,1,3) = 2 está entre 1 y 3, proposición verdadera.
Es importante el orden de los términos.
d) P(x,y,z): La suma de x y y es z.
P(2,3,5): La suma de 2 y 3 es 5, proposición verdadera.
P(1,3,6): La suma de 1 y 3 es 6, proposición falsa.
El predicado de la primera función es: “es mayor que”; de la segunda “es hermano de”, de
la tercera “está entre y “, y finalmente en la cuarta: “la suma de y es”
Notemos que en la primera función se realiza una comparación, en la segunda se hace

mención a un parentesco y en la tercera función se hace referencia a una ubicación, está puede ser
de calles, ciudades e incluso países, etc.
En general para obtener funciones de dos o tres variables con un solo predicado se trata de
establecer una relación entre las variables.
Consideremos ahora las funciones: A(x), B(y) y C(z), al combinarlas con los conectivos
lógicos obtenemos funciones de tres variables, como:
a) D(x,y,z)=A(x) (B(y) C(z))

b) E(x,y,z)=(A(x) B (y)) (A(x) C(z))
Continuando de ese modo podremos obtener funciones de n variables.
De lo anterior podemos concluir que se pueden formar funciones lógicas de una o má s

variables con uno o más predicados. Una función proposicional, por si misma no es verdadera ni

110
falsa. Sin embargo, al sustituir x por un valor se convierte en proposición y por tanto, puede ser
verdadera o falsa.
En álgebra, la variable x se sustituye por números reales, complejos, racionales enteros, etc.
Se plantea esta idea diciendo que el universo de la variable x es el conjunto de los números
reales, o de los complejos, o de los enteros etc., la selección de estos conjunto depende del
propósito del problema.
Considere las siguientes ecuaciones del álgebra elemental.
1. (x-2)=4
2. x2+1=0
3. 2x2-7x+6=0
4. x2+4x+4=(x+2)2
Cada una de estas ecuaciones son funciones proposicionales. En la ecuación 1) si x se

sustituye por un número real, se obtiene una proposición, esta proposición sólo es verdadera
cuando se reemplaza x por 6. En la ecuación 2) no hay ningún número real que al sustituir a x de
una proposición verdadera. Sin embargo si el universo de x incluye a los números complejos,
entonces hay dos valores que al sustituir a x dan enunciados verdaderos. En 3) hay dos valores
reales que al sustituir a x dan proposiciones verdaderas, sin embargo si el universo de x incluye
sólo los valores enteros hay un único valor de x que da una proposición verdadera. Finalmente en
la ecuación 5) cualquier número que sustituya a x, da proposiciones verdaderas, esto significa que
podemos reescribir la ecuación 4) diciendo que para cualquier x, x2+4x+4=(x+2)2. Observe que
4) es una proposición y no una función proposicional.
Las funciones proposicionales no siempre son expresiones matemáticas por lo que el valor
de la variable no siempre es numérico. Para saber como son los valores que toma la variable x se
especifica que los valores son miembros de una clase o conjunto particular. Esta clase se conoce
como el universo del discurso o dominio de la variable. Esto nos permitirá simbolizar las
funciones proposicionales.
1.3.2 Uso de cuantificadores: función de una, dos y tres variables
La palabra cuantificador hace referencia a cantidad, nos centraremos en dos cantidades, las
que se refieren a pocos elementos y a todos, dentro de un cierto universo.
Definición 1.3.4 ( Cuantificadores )

Los cuantificadores indican la frecuencia con la cual es verdadera una cierta frase.
Hay dos tipos de cuantificadores:
Universal: Indica que una frase siempre es verdadera.
Existencial: Indica que una frase es verdadera en algunas ocasiones.

111
Definición 1.3.5 (Cuantificador universal)

Sea A una expresión y x una variable . Si deseamos indicar que A es verdadero para todos
los posibles valores de x, escribimos xA. Aquí x se denomina cuantificador universal, y A se
denomina ámbito o alcance del cuantificador.
El cuantificador universal, simbolizado por y que se lee “para todo”, corresponde en el

lenguaje ordinario a expresiones como: “para todo”, “cada”, “para cada, “todo”, “cualquiera”,
etc.; todas aquellas frases que nos indiquen todos los elementos de un conjunto. Es posible usar el
cuantificador universal para indicar negación y este se presenta en expresiones como: “ninguno”,
“nadie”, “para ningún”, “nada” y “no”.
Ejemplo 1.3.5
Proposiciones que involucran el cuantificador universal.
a) Todos los comunistas son marxistas.
b) Ningún comunista es marxista.
c) No todos los comunistas son marxistas.
Definición 1.3.6 (Cuantificador existencial)

Sea A una expresión y sea x una variable. Si deseamos indicar que A es verdadero para
cuando menos un valor de x, escribiremos xA. Esta frase se lee “ existe un x tal que”. Aquí x se
denomina cuantificador existencial, y se dice que A es el ámbito o alcance del cuantificador
existencial.
El cuantificador existencial, simbolizado por y que se lee “existe”, corresponde en el

lenguaje ordinario a expresiones como: “existe algún”, “para algunos”, “para ciertos”, “algo”,
“algún”, “existe al menos uno”, etc.; todas aquellas frases que nos indiquen un número de
elementos distinto del total. No se asocia una frase de negación con el cuantificador existencial
ya que son algunos elementos los que cumplen la propiedad y también algunos los que no
cumplen la propiedad, así regularmente cuando se trata de negación esta se agrega en la
proposición.
Ejemplo 1.3.6
a) Algunos comunistas son marxistas.
b) No hay comunistas y marxistas.
c) Hay comunistas que no son marxistas.
Traducción del lenguaje ordinario a la lógica cuantificacional
El cuantificador universal se expresa por medio de una implicación.
Ejemplo 1.3.7
Considere las proposiciones dadas en el ejemplo 1.3.5y represente cada proposición como
una función con cuantificadores de manera enunciativa y simbólica.

112
a) Todos los comunistas son marxistas.

De forma enunciativa:
Para toda x, si x es comunista entonces x es marxista.
De forma simbólica:
C(x)= x es comunista.
M(x)= x es marxista.
x (C(x) M(x)).
b) Ningún comunista es marxista.

Para todo x, si x es comunista entonces x no es marxista.
x (C(x) M (x ) ).
c) No todos los comunistas son marxistas.

No para todo x, si x es comunista entonces x es marxista.
x (C(x) M(x)).
El cuantificador existencial se expresa en forma de conjunción.
Ejemplo 1.3.8
Considere las proposiciones del ejemplo 1.3.6 y represente cada proposición como una
función con cuantificadores de manera enunciativa y simbólica.
a) Algunos comunistas son marxistas.

Existe x, tal que x es comunista y x es marxista.
x (C(x) M(x)).
b) No hay comunistas y marxistas.

No existe x, tal que x sea comunista y x sea marxista.
x (C(x) M(x)).
c) Hay comunistas que no son marxistas.

De forma enunciativa.
De forma simbólica.
x (C(x) M (x ) ).
Ejemplo 1.3.9
Expresar de manera simbólica los siguientes enunciados.

113
a) Todos los gatos tienen cola.

Para todo x, si x es un gato, entonces x tiene cola.
G(x)=x es un gato.
C(x)=x tiene cola.
x(G(x) C(x))
Otra forma de expresar esta frase es:

y(G(y) C(y))
Aquí la variable ligada es y en lugar de x. En general el nombre de la variable
utilizada para la cuantificación es irrelevante.
b) No todo lo que brilla es oro.

No es cierto que, para todo x, si x brilla entonces x es oro.
O(x)=x es oro.
B(x)=x brilla.
Usando el cuantificador universal:
xBx Ox
Usando el cuantificador existencial
x(B(x) O x
c) Algunos elementos son radiactivos.

E(x): x es un elemento.
R(x): x es radiactivo.
Existe un x tal que, x es un elemento y x es radiactivo.
x (E(x) R(x))
d) Todo mundo tiene suerte de vez en cuando.

Para todo x, x tiene suerte de vez en cuando.
S(x): x tiene suerte de vez en cuando.
xS(x)
e) hay personas a las cuales les gusta la carne cruda.

Algunas personas les gusta la carne cruda.
Existe un x tal que , a x le gusta la carne cruda.
P(x): a x le gusta la carne cruda.
xP(x)
f) Existen objetos azules.

Existe al menos un x tal que, x es azul.
B(x): x es un objeto.
A(x): x es azul.
x (B(x) A(x))
Ejemplo 1.3.10
Cuantifique los siguientes enunciados:

114
a) Las siguientes oraciones quieren decir lo mismo.

Cada entero es par o impar.
Todo entero es par o impar.
Un entero es par o impar.
Sea x cualquier entero, Entonces x es par o impar.
Para toda x, si x es un entero, entonces x es par o impar.
b) Todos los hombres son mortales

Para toda x, si x es un hombre, entonces x es mortal
c) Todos los planetas tienen atmósfera

Para toda x, si x es un planeta, entonces x tiene atmósfera
d) Todos los gordos son simpáticos

Para toda x, si x es un gordo, entonces x es simpático.
e) Nadie es perfecto
Para toda x, Si x es una persona, entonces no es perfecto.
f) Ningún niño es malvado

Para toda x, si x es un niño, entonces no ocurre que x es malvado.
g) Ningún perro maúlla

Para toda x, si x es un perro, entonces x no maúlla
h) Ningún Guatemalteco es Europeo

Para toda x, si x es guatemalteco, entonces x no es Europeo.
i) Todos los Tabasqueños son Mexicanos

Para toda x, si x es tabasqueño, entonces x es mexicano.
j) Cualquier entero es real

Para toda x, si x es un entero, entonces x es real.
k) Todos los perros son mamíferos

Para toda x, si x es un perro, entonces x es mamífero.
También se pueden tener frases anidadas, es decir, que impliquen más de un

cuantificador.
Ejemplo 1.3.11
a) Hay alguien que conoce a todo mundo.

Esta expresión puede parafrasearse de la siguiente manera:
Existe un x tal que, x conoce a todo mundo.
x, x conoce a todo mudo

115
“x conoce a todo mundo”, puede reescribirse:

Para todo y, es cierto que x conoce a y.
La frase completa sería;

“Existe un x, tal que para todo y x conoce a y.
C(x,y): x conoce a y.
P(x): x es una persona.
x[P(x) y(P(y C(x,y))]

x yC(x,y)
b) Todo el mundo tiene alguien que es su madre.

M(x,y): x es madre de y.
Mu(x): x es una mujer.
“Alguien es madre de y”
x(Mu(x) M(x,y))
Lo anterior es cierto para todo y.
y [P(y) x(Mu(x) M(x,y))]
Ejemplo 1.3.12
Cuantifique los siguientes enunciados.
a) Dado cualquier enteo positivo, existe un entero positivo mayor.
Para toda x, si x es un entero positivo, entonces existe y tal que y es un entero positivo y es
mayor que x.
b) Alguien amo a todos.

Existe x, tal que x es una persona y para todo y, si y es una persona entonces x ama a y.
c) Todos aman a alguien.

Para toda x,, si x es una persona entonces existe y tal que y es una persona y x ama a y.
d) Alguien ama a alguien.

Existe x, tal que x es una persona y existe y tal que y es una persona y x ama a y.
e) Todos aman a todos.

Para toda x, si x es una persona entonces para toda y si y es una persona entonces x ama a y.
Ejemplo 1.3.13
a) Sean P(x): x 0.
Q(x): x2 0.
R(x): x2–3x –4 = 0.
S(x): x2 – 3 > 0.
Donde el universo de discurso son todos los números reales.
Determine si las siguientes proposiciones son falsas o verdaderas?
i. x[P(x) R(x)] Verdadera

116
ii. x[P(x) Q(x)] Verdadera

iii. x[Q(x) S(x)] Falsa
iv. x[R(x) S(x)] Falsa
b) Sea P(x,y): y-x=y–x2.

El universo de discurso de las variables x e y son los números enteros.
Determine el valor de verdad de las siguientes proposiciones.
i) P(0,0) Verdadera
ii) P(0,1) Verdadera
iii) y (P(0,y)) Verdadera
iv) xy P(x,y) Falsa
v) y xP(x,y) Falsa
vi) P(1,1) Verdadera
vii) P(0,3) Verdadera
viii) x yP(x,y) Falsa
ix) yP(1,y) Verdadera
x) y xP(x,y) Verdadera
Ejemplo 1.3.14
Exprese los siguiente en forma simbólica. El universo de discurso está formado por
los reales positivos.
a) No existe un número real positivo mínimo.
P(x): x es un # real positivo.
Q(x): x es mínimo.
x ( P(x) Q(x))
x (P(x) Qx )
b) Existe un número real positivo igual a su cuadrado.

P(x):x es un real positivo. Q(x):x es igual a su cuadrado.
x (P(x) Q(x))
Ejemplo 1.3.14
Sean los predicados diádicos:
P(x, y )=x es amigo de y, Q(x, y)=x da la mano a y y R(x, y)=x engaña a y.
Los monádicos:
A(x)=x pide armas, B(x)=x pide ayuda cultural y C(x)=x puede evadir los impuestos.
Y las constantes:
a:Carlos, b:Saúl, c:Nicolás, d:Bruno y e:César.
Simbolice los siguientes enunciados

a) Si Saúl pide armas, entonces César dará la mano a Nicolás, a menos que alguien pida ayuda
cultural.
Si Saúl pide armas entonces no existe x tal que si x pide ayuda cultural entonces César dará
la mano a Nicolás.

117
A(b) x (B(x) Q(e, c))
b) Si nadie pide armas entonces, o Carlos engaña a Saúl o Saúl no es amigo de Bruno.
Para toda x, si x no pide armas entonces Carlos engaña a Saúl o Saúl no es amigo de Bruno.
x ( A(x) R(a, b) P(b, d ))
c) Bruno pedirá armas sólo si algún amigo suyo le engaña.

Bruno pedirá armas sólo si existe x tal que x es amigo de Bruno y x engaña a Bruno.
A (d) x (P(x, d) R(x, d)
d) Carlos no engañara a nadie que sea amigo de Nicolás

Para toda x, si x es amigo de Nicolás entonces Carlos no engaña a x
x( P(x, c) R( a , x )
e) Aunque todo el mundo pide ayuda cultural, nadie dará la mano a nadie a menos que Carlos
pueda evadir los impuestos.
Para toda x, x pide ayuda cultural y si Carlos no puede evadir impuestos entonces para toda
x y para toda y, x no da la mano a y.
x B(x) ( C (a) x y Q x, y )
1.3.3 Uso de cuantificadores: función de una, dos y tres variables
La palabra cuantificador hace referencia a cantidad, nos centraremos en dos cantidades, las
que se refieren a pocos elementos y a todos, dentro de un cierto universo.
Definición 1.3.4 ( Cuantificadores )

Los cuantificadores indican la frecuencia con la cual es verdadera una cierta frase.
Hay dos tipos de cuantificadores:
Universal: Indica que una frase siempre es verdadera.
Existencial: Indica que una frase es verdadera en algunas ocasiones.
Definición 1.3.5 (Cuantificador universal)

Sea A una expresión y x una variable . Si deseamos indicar que A es verdadero para todos
los posibles valores de x, escribimos xA. Aquí x se denomina cuantificador universal, y A se
denomina ámbito o alcance del cuantificador.
El cuantificador universal, simbolizado por y que se lee “para todo”, corresponde en el

lenguaje ordinario a expresiones como: “para todo”, “cada”, “para cada, “todo”, “cualquiera”,

118
etc.; todas aquellas frases que nos indiquen todos los elementos de un conjunto. Es posible usar el
cuantificador universal para indicar negación y este se presenta en expresiones como: “ninguno”,
“nadie”, “para ningún”, “nada” y “no”.
Ejemplo 1.3.5
d) Todos los comunistas son marxistas.
e) Ningún comunista es marxista.
f) No todos los comunistas son marxistas.
Definición 1.3.6 (Cuantificador existencial)

Sea A una expresión y sea x una variable. Si deseamos indicar que A es verdadero para
cuando menos un valor de x, escribiremos xA. Esta frase se lee “ existe un x tal que”. Aquí x se
denomina cuantificador existencial, y se dice que A es el ámbito o alcance del cuantificador
existencial.
El cuantificador existencial, simbolizado por y que se lee “existe”, corresponde en el

lenguaje ordinario a expresiones como: “existe algún”, “para algunos”, “para ciertos”, “algo”,
“algún”, “existe al menos uno”, etc.; todas aquellas frases que nos indiquen un número de
elementos distinto del total. No se asocia una frase de negación con el cuantificador existencial
ya que son algunos elementos los que cumplen la propiedad y también algunos los que no
cumplen la propiedad, así regularmente cuando se trata de negación esta se agrega en la
proposición.
Ejemplo 1.3.6
d) Algunos comunistas son marxistas.
e) No hay comunistas y marxistas.
f) Hay comunistas que no son marxistas.
Traducción del lenguaje ordinario a la lógica cuantificacional
El cuantificador universal se expresa por medio de una implicación.
Ejemplo 1.3.7
Considere las proposiciones dadas en el ejemplo 1.3.5y represente cada proposición como
una función con cuantificadores de manera enunciativa y simbólica.
d) Todos los comunistas son marxistas.

Para toda x, si x es comunista entonces x es marxista.
C(x)= x es comunista.
M(x)= x es marxista.
x (C(x) M(x)).

119
e) Ningún comunista es marxista.

Para todo x, si x es comunista entonces x no es marxista.
x (C(x) M (x ) ).
f) No todos los comunistas son marxistas.

No para todo x, si x es comunista entonces x es marxista.
x (C(x) M(x)).
El cuantificador existencial se expresa en forma de conjunción.
Ejemplo 1.3.8
Considere las proposiciones del ejemplo 1.3.6 y represente cada proposición como una
función con cuantificadores de manera enunciativa y simbólica.
d) Algunos comunistas son marxistas.

x (C(x) M(x)).
e) No hay comunistas y marxistas.

No existe x, tal que x sea comunista y x sea marxista.
x (C(x) M(x)).
f) Hay comunistas que no son marxistas.

De forma enunciativa.
De forma simbólica.
x (C(x) M (x ) ).
Ejemplo 1.3.9
Expresar de manera simbólica los siguientes enunciados.
c) Todos los gatos tienen cola.

Para todo x, si x es un gato, entonces x tiene cola.
G(x)=x es un gato.
C(x)=x tiene cola.
x(G(x) C(x))

120
Otra forma de expresar esta frase es:

y(G(y) C(y))
Aquí la variable ligada es y en lugar de x. En general el nombre de la variable
utilizada para la cuantificación es irrelevante.
d) No todo lo que brilla es oro.

No es cierto que, para todo x, si x brilla entonces x es oro.
O(x)=x es oro.
B(x)=x brilla.
Usando el cuantificador universal:
xBx Ox
Usando el cuantificador existencial
x(B(x) O x
g) Algunos elementos son radiactivos.

E(x): x es un elemento.
R(x): x es radiactivo.
Existe un x tal que, x es un elemento y x es radiactivo.
x (E(x) R(x))
h) Todo mundo tiene suerte de vez en cuando.

Para todo x, x tiene suerte de vez en cuando.
S(x): x tiene suerte de vez en cuando.
xS(x)
i) hay personas a las cuales les gusta la carne cruda.

Algunas personas les gusta la carne cruda.
Existe un x tal que , a x le gusta la carne cruda.
P(x): a x le gusta la carne cruda.
xP(x)
j) Existen objetos azules.

Existe al menos un x tal que, x es azul.
B(x): x es un objeto.
A(x): x es azul.
x (B(x) A(x))
Ejemplo 1.3.10
Cuantifique los siguientes enunciados:
l) Las siguientes oraciones quieren decir lo mismo.

Cada entero es par o impar.
Todo entero es par o impar.
Un entero es par o impar.
Sea x cualquier entero, Entonces x es par o impar.
Para toda x, si x es un entero, entonces x es par o impar.

121
m) Todos los hombres son mortales

Para toda x, si x es un hombre, entonces x es mortal
n) Todos los planetas tienen atmósfera

Para toda x, si x es un planeta, entonces x tiene atmósfera
o) Todos los gordos son simpáticos

Para toda x, si x es un gordo, entonces x es simpático.
p) Nadie es perfecto
Para toda x, Si x es una persona, entonces no es perfecto.
q) Ningún niño es malvado

Para toda x, si x es un niño, entonces no ocurre que x es malvado.
r) Ningún perro maúlla

Para toda x, si x es un perro, entonces x no maúlla
s) Ningún Guatemalteco es Europeo

Para toda x, si x es guatemalteco, entonces x no es Europeo.
t) Todos los Tabasqueños son Mexicanos

Para toda x, si x es tabasqueño, entonces x es mexicano.
u) Cualquier entero es real

Para toda x, si x es un entero, entonces x es real.
v) Todos los perros son mamíferos

Para toda x, si x es un perro, entonces x es mamífero.
También se pueden tener frases anidadas, es decir, que impliquen más de un

cuantificador.
Ejemplo 1.3.11
c) Hay alguien que conoce a todo mundo.

Esta expresión puede parafrasearse de la siguiente manera:
Existe un x tal que, x conoce a todo mundo.
x, x conoce a todo mudo
“x conoce a todo mundo”, puede reescribirse:
Para todo y, es cierto que x conoce a y.
La frase completa sería;

“Existe un x, tal que para todo y x conoce a y.
C(x,y): x conoce a y.

122
x[P(x) y(P(y C(x,y))]

x yC(x,y)
d) Todo el mundo tiene alguien que es su madre.

M(x,y): x es madre de y.
Mu(x): x es una mujer.
“Alguien es madre de y”
x(Mu(x) M(x,y))
Lo anterior es cierto para todo y.
y [P(y) x(Mu(x) M(x,y))]
Ejemplo 1.3.12
Cuantifique los siguientes enunciados.
f) Dado cualquier enteo positivo, existe un entero positivo mayor.
Para toda x, si x es un entero positivo, entonces existe y tal que y es un entero positivo y es
mayor que x.
g) Alguien amo a todos.

Existe x, tal que x es una persona y para todo y, si y es una persona entonces x ama a y.
h) Todos aman a alguien.

Para toda x,, si x es una persona entonces existe y tal que y es una persona y x ama a y.
i) Alguien ama a alguien.

Existe x, tal que x es una persona y existe y tal que y es una persona y x ama a y.
j) Todos aman a todos.

Para toda x, si x es una persona entonces para toda y si y es una persona entonces x ama a y.
Ejemplo 1.3.13
b) Sean P(x): x 0.
Q(x): x2 0.
R(x): x2–3x –4 = 0.
S(x): x2 – 3 > 0.
Donde el universo de discurso son todos los números reales.
Determine si las siguientes proposiciones son falsas o verdaderas?
v. x[P(x) R(x)] Verdadera
vi. x[P(x) Q(x)] Verdadera
vii. x[Q(x) S(x)] Falsa
viii. x[R(x) S(x)] Falsa
b) Sea P(x,y): y-x=y–x2.

El universo de discurso de las variables x e y son los números enteros.
Determine el valor de verdad de las siguientes proposiciones.

123
xi) P(0,0) Verdadera

xii) P(0,1) Verdadera
xiii) y (P(0,y)) Verdadera
xiv) xy P(x,y) Falsa
xv) y xP(x,y) Falsa
xvi) P(1,1) Verdadera
xvii) P(0,3) Verdadera
xviii) x yP(x,y) Falsa
xix) yP(1,y) Verdadera
xx) y xP(x,y) Verdadera
Ejemplo 1.3.14
Exprese los siguiente en forma simbólica. El universo de discurso está formado por
los reales positivos.
c) No existe un número real positivo mínimo.
P(x): x es un # real positivo.
Q(x): x es mínimo.
x ( P(x) Q(x))
x (P(x) Qx )
d) Existe un número real positivo igual a su cuadrado.

P(x):x es un real positivo. Q(x):x es igual a su cuadrado.
x (P(x) Q(x))
Ejemplo 1.3.14
Sean los predicados diádicos:
P(x, y )=x es amigo de y, Q(x, y)=x da la mano a y y R(x, y)=x engaña a y.
Los monádicos:
A(x)=x pide armas, B(x)=x pide ayuda cultural y C(x)=x puede evadir los impuestos.
Y las constantes:
a:Carlos, b:Saúl, c:Nicolás, d:Bruno y e:César.
Simbolice los siguientes enunciados

f) Si Saúl pide armas, entonces César dará la mano a Nicolás, a menos que alguien pida ayuda
cultural.
Si Saúl pide armas entonces no existe x tal que si x pide ayuda cultural entonces César dará
la mano a Nicolás.
A(b) x (B(x) Q(e, c))
g) Si nadie pide armas entonces, o Carlos engaña a Saúl o Saúl no es amigo de Bruno.
Para toda x, si x no pide armas entonces Carlos engaña a Saúl o Saúl no es amigo de Bruno.
x ( A(x) R(a, b) P(b, d ))

124
h) Bruno pedirá armas sólo si algún amigo suyo le engaña.

Bruno pedirá armas sólo si existe x tal que x es amigo de Bruno y x engaña a Bruno.
A (d) x (P(x, d) R(x, d)
i) Carlos no engañara a nadie que sea amigo de Nicolás

Para toda x, si x es amigo de Nicolás entonces Carlos no engaña a x
x( P(x, c) R( a , x )
j) Aunque todo el mundo pide ayuda cultural, nadie dará la mano a nadie a menos que Carlos
pueda evadir los impuestos.
Para toda x, x pide ayuda cultural y si Carlos no puede evadir impuestos entonces para toda
x y para toda y, x no da la mano a y.
x B(x) ( C (a) x y Q x, y )
2.2 OPERACIONES ENTRE CONJUNTOS
Los conjuntos se pueden representar gráficamente por medio de Diagramas de Venn, en

estos diagramas, llamados así en honor de matemático británico Jhon Venn (1834–1923), el
conjunto universal se representa por un rectángulo, los subconjuntos del conjunto universal están
representados por círculos. El resultados de las operaciones entre subconjuntos se pueden ilustrar
mediante áreas sombreadas.
2.2.1 Unión
Definición 2.2.1 (Unión)

La unión (o reunión) de dos conjuntos A y B, denotada por A B (que se lee “A
unión B”) es un nuevo conjunto formado por los elementos que pertenecen a A o a
B o a ambos conjuntos.
A B={x | x A x B}.
A B={x | x A o x B}.
Si x A B entonces x A ó x B o x pertenece a ambos conjuntos.

x Ay x B
Lo cual se puede presentar como x Ay x B
x Ay x B
Representación gráfica

125
A B
Ejemplo 2.2.1
Considere los siguientes conjuntos: A={1,2,3,4}, B={2,4,6} y C={2,3,5,7}.
a) A B={1,2,3,4,6}.
b) A C={1,2,3,4,5,7}.
c) B C={2,3,4,5,6,7}.
2.2.2 Intersección
Definición 2.2.2 (Intersección)

La intersección de dos conjuntos A y B, denotada por A B (que se lee “ A intersección
B”), es un nuevo conjunto formado por los elementos que pertenecen a A y a B al mismo tiempo,
es decir, por los elementos comunes a ambos conjuntos.
A B={x | x A x B}.
A B={x | x A y x B}.
Definición 2.2.3 (Conjuntos ajenos o disjuntos)

Sean A y B dos conjuntos, decimos que A y B son ajenos o disjuntos si A y B no tienen
elementos comunes, esto si A B= .
A B A B=
Ejemplo 2.2.2
A={1,2,3,4} B={2,4,6} C={2,3,5,7}
a) A B={2,4}.
b) A C={2,3}.
c) B C={2}.
d) A B C={2}.
2.2.3 Complemento
Definición 2.2.4 (Complemento)

126
Sea A U un conjunto. El complemento de A denotado por A, A’, AC ó U–A, se define

como el conjunto de todos los elementos que están en U pero no están en A. Simbólicamente:
A={x | x U x A}.
A={x | x U y x A}.
Es decir, El complemento de A es el conjunto de los todos los elementos que no están en el

conjunto A. Simbólicamente: A={x | x A}.
Ejemplo 2.2.3
Sea U=conjunto de los números enteros y A={x | x es un entero y x 4}. El complemento de
A es: Ā={x | x es un entero y x<4}.
Ejemplo 2.2.4
Sean U={0,1,2,3,4,5,6,7,8}, A={1,2,3,4} y B={2,4,6}.
a) A ={0,5,6,7,8}
b) B = {0,1,3,5,7,8}
c) A B = {0,5,7,8}
d) A B = {0,1,3,5,6,7,8}
2.2.4 Diferencia
Definición 2.2.5.( Complemento relativo o diferencia de conjuntos )

Sean A y B conjuntos, definimos el complemento relativo de B en A o diferencia de A y B,
que se denota por A–B, (que se lee “A menos B”), como el conjunto de todos los elementos que
pertenecen a A pero no pertenecen a B. Simbólicamente:
A–B={x | x A x B}
A–B={x | x A y x B}
A-B
Ejemplo 2.2.5
a) Sean A={a,b,c} y B={c,d}.
A–B={a,b} B–A={d}.

127
b) A={3,4,5,6} B={4,5}.
A–B={3,6} B–A={}.
c) A={1,2,3} B={6,7}.
A–B={1,2,3} B–A={6,7}.
2.2.5 Diferencia simétrica
Definición 2.2.6 (Diferencia simétrica)

La diferencia simétrica de dos conjuntos A y B, que se denota por A B (que se lee “A
diferencia simétrica B”), es el conjunto formado por los elementos que están en A o en B, pero
que no pertenecen simultáneamente a ambos.
A B=(A B)–(A B)={x | x (AoB) y x (A B)}.
A B=(A-B) (B-A)={x | (x A y x B) ó (x B y x A)}.
A B
Ejemplo 2.2.6
Sean A={1,2,3,4}, B={2,4,6} y C={2,3,5,7}.
a) A B={1,3,6}.
b) A C={1,4,5,7}.
c) B C={3,4,5,6,7}.
Ejemplo 2.2.7
Podemos decir que los conjuntos A B C y (A B C)–(A B C) son iguales?
(A B C)–(A B C)={1,2,3,4,5,6,7}–{2}={1,3,4,5,6,7}.
(A B) C={1,2,5,6,7}.
A (B C)={1,2,5,6,7}.
Por lo tanto no son iguales.
2.2.6 Producto cartesiano
Definición 2.2.7 (Producto cartesiano)

Sean A y B conjuntos. Se llama producto cartesiano de A y B al conjunto de todos los pares
ordenados (x,y) tal que x A y y B y se denota por AxB. Simbólicamente:
AxB={(x,y) | x A y y B}
Ejemplo 2.2.8

128
Sean A={1,2,3} y B={2,4,6}.

AxB={(1,2),(1,4),(1,6),(2,2),(2,4),(2,6),(3,2),(3,4),(3,6)}.
Ejemplo 2.2.9
Sean U={a,b,c,d,e,f,g,h,k}, A={a,b,c,g}, B={d,e,f,g}, C={a,c,f} y D = {f, h, k}.
a) A B={a,b,c,d,e,f,g}.
b) A C={a,c}.
c) A–B={a,b,c}.
d) B–A={d,e,f}.
e) A ={d,e,f,h,k}.
f) A B={a,b,c,d,e,f}.
g) D C={h,k,a,c}.
h) CxD={(a,f),(a,h),(a,k),(c,f),(c,h),(c,k),(f,f),(f,h),(f,k)}.
Ejemplo 2.2.10
Sean A={1,2,3,4}, B={2,4,5,6}, C={3,4,6,7} y U={1,2,3,...,8}, Determinar:
a) AC  B 3,4  2,4,6,7 2,3,4,5,6
b) A  B 5,6,7,8  1,3,7,8 1,3,5,6,7,8
c) A B C 1,3,5,6  3,4,6,7 3,6

129
Ejemplo 2.2.11
Considere los conjuntos definidos en el ejemplo 2.2.10.
Comprobar si los siguientes enunciados son falsos o verdaderos.
a) A  A  B A {1,2,3,4}={1,2,3,4} Verdadero
b) A  C  B A {1,2,3,4,6}={1,2,3,4} Falso
c) A B A {1,3} {1,2,3,4} Verdadero
d) B  B  C B {2,4,5,6} {2,4,5,6} Falso
e) A  B A B A B {1,3,5,6} {1,2,3,4,5,6} Falso
Ejemplo 2.2.12
Representa simbólicamente el área iluminada en los siguientes diagramas
a)
b)
c)
d)

130
Ejemplo 2.2.13
Sabiendo que y m, n, t , x y m, n, p, q, r y x y p, q
Hallar:
a) x={m,n,p,q}.
b) y={r,p,q}
Demostración de propiedades
Haciendo uso de las definiciones de las operaciones de conjuntos y de algunas propiedades

básicas es posible mostrar otras propiedades como las siguientes.
Propiedad 2.2.1: A–B=A B

Demostración
Como se trata de una igualdad primero hay que mostrar
a) A–B A B
b) A B A–B
a) Mostraremos la contención mediante pertenencia, esto es tomemos un elemento en A–B y

veamos que este está en A B . Simbólicamente:
x A–B x A B .
Como x A–B entonces x A y x B, luego x A y x B , así x A B como se quería

mostrar.
b) x A B x A–B
Como x A B entonces x A y x B , de donde x A y x B, así x A–B como se quería
mostrar.
Propiedad 2.2.2: Si A C=B C y A–C=B–C entonces A=B.

Demostración
La propiedad planteada es una proposición condicional, por lo cual tenemos:
Hipótesis: A C=B C y A–C=B–C, y
Conclusión: A=B.
Debemos mostrar la igualdad de los conjuntos A y B que cumplen las condiciones
señaladas en la hipótesis.
a) A B.
b) B A.
a) x A x B.
Partimos de que x A, pero esto no nos lleva a algún resultado y además no es posible usar
la hipótesis dada, así que agregaremos una hipótesis adicional, esta es suponer que x está o no en
C, luego tenemos:
1. x A y x C.
2. x A y x C.

131
De (1) se tiene que x A C y por hipótesis A C=B C, así x B C de donde x B y x C,

el que x C ya se sabía, por lo que obtenemos que x B, y esto es lo que se quería mostrar, así
A B.
De (2) se tiene que x A–C y por hipótesis A–C=B–C, así x B–C de donde x B y x C, el
que x C ya se sabía, por lo que obtenemos que x B, y esto es lo que se quería mostrar, así A B.
b) La demostración es análoga al caso (a).
Propiedad 5:Si A,B U, las proposiciones siguientes son equivalentes.

a) A B.
b) A B=B.
c) A B=A.
d) B A .
Demostración
Para mostrar la equivalencia se necesita mostrar (a) (b), (b) (c), (c) (d) y (d) (a)
(a) (b) Si A B entonces A B=B.

Hipótesis: A B.
Conclusión: A B=B.
1. A B B.
2. B A B.
1. x A B x B.
x A y x B
Como x A B entonces x A ó x B, esto es x A y x B , en el primero y tercer
x A y x B
x B
caso se tiene que x B y en el segundo se tiene que x A, esto es x A
x B
Para llegar a la conclusión pedida hay que mostrar que x B para cualquier caso, así
falta de verificar que esto se cumple si x A.
Como x A y por hipótesis A B entonces x B.
Por lo tanto para toda x se cumple que x B.
2. x B x A B, como x B entonces x pertenece a B unido con cualquier conjunto, en

particular con A, esto es x A B, ya que es suficiente que x este en un conjunto para
pertenecer a la unión.
(b) (c) Si A B=B entonces A B=A.

Hipótesis: A B=B.
Conclusión: A B=A.

132
Hay que mostrar que:

1) A B A.
2) A A B.
1) x A B x A.
Como x A B entonces x A y x B, así encontramos que x A.
2) x A x A B.
Tenemos que x A y como hipótesis que A B=B, buscando relacionar la hipótesis
con lo que tenemos, sucede
Si x A entonces x A B=B, así x B.
Por lo tanto x A y x B, con lo cual x A B.
(c) (d) Si A B=A entonces B A .

Hipótesis: A B=A.
Conclusión: B A .
Hay que mostrar que si x B entonces x A .
Como x B entonces x B, luego x A B que por hipótesis es igual a A, luego x A, por lo
tanto x A .
(d) (a) Si B A entonces A B.

Hipótesis: B A
Conclusión: A B
Hay que mostrar que si x A x B.
Supongamos que la conclusión no es válida, esto es, que x B, así x B y por hipótesis
x A , con lo cual x A, lo cual no es cierto ya que partimos de considerar que x A, luego x B.
De este modo queda mostrado que las proposiciones dadas son equivalentes.
Propiedades del álgebra de conjuntos

A (B C)=(A B) (A C).
1) Idempotencia A (B C)=(A B) (A C).
A A=A. 5) dentidad
A A=A. A =A.
A U=A.
2) Conmutativa
A B=B A. 6) Dominación
A B=B A. A = .
A U=U.
3) Asociativa
(A B) C=A (B C).
7) Inversas
(A B) C=A (B C).
A A U.
4) Distributiva A A .

133
8) Complemento
A =A.
U= .
=U.
9) De Morgan
A B A B.
A B A B
10) Absorción
A (A B)=A.
A (A B)=A.

94
Unidad III: Relaciones Ejercicios
Ejemplo 2.3.1
Use las propiedades para simplificar el siguiente conjunto
(A B) C B
A B C B De Morgan
(A∪B) C) B Complemento
(A∪B) (C B) Asociativa
(A∪B) (B C) Conmutativa
((A∪B) B) C Asociativa
(B (B∪A)) C Conmutativa
B C Absorción
Una introducción a las matemáticas de la computación 132

Ejemplo 2.3.2
Si A B=(A B) A B Demuestre que A B A B.
A B = A B (A B) Definición
A B (A B) De Morgan
(A B) A B Complemento
A B A A B B Distributiva
A A) (A B (A B) (B B) Distributiva
U ( A B) ( A B) U ) Complemento
( A B) ( A B) Identidad
A B A B De morgan
A B Definición
Ejemplo 2.3.3
Demostrar que A  A  B A  B
A A  A B Distributiva
Ø  A B Inversa
A B Identidad
Ejemplo 2.3.4
Demuestre que P Q P Q P
P Q P Q De Morgan
P Q P Q Complemento
P Q Q Distributiva
P Ø Complemento
P Identidad
Ejemplo 2.3.5
Demuestre que A  B  A  B  C Ø
A A  B B C Conmutativa y asociativa
Ø  BC Complemento
Ø Identidad
Ejemplo 2.3.6
Demuestre que A  B  C  A  B  C U
 B 
A
 C   B 
A C
M M
M M Cambio de variable
U Complemento

Ejercicios: unidad II
2.1 Escribir el conjunto dado enlistando sus elementos.

a) El conjunto de todos los enteros positivos nones menores que 10.
b) {x | x y x2 <12}.
2.2 Escriba de la forma {x | P(x)}, donde P(x) es la propiedad que los elementos del conjunto
tienen en común.
a) {2,4,6,8,10}.
b) {1,4,9,16,25,36}.
c) {-2, -1, 0, 1, 2}.
2.3 Sea A={1,2,5,8,11}. Responda si lo siguiente es falso o verdadero.

a) {5,1}⊆A.
b) {8,1} A.
c) {1,6}⊈A.
d) {1,8,2,11,5}⊈A.
e) ∅⊆A.
f) {2}⊆A.
g) A⊆{11,2,5,1,8,4}.
h) {3}∉A.
2.4 Si un conjunto A tiene 63 conjuntos propios, ¿cuál es |A|?.
2.5 Si A={1,2,3,4,5,6,7}, determínese el número de:

a) Subconjuntos de A.
b) Subconjuntos no vacíos de A.
c) Subconjuntos propios de A.
d) subconjuntos propios no vacíos de A.
2.6 Si un conjunto A tiene 64 subconjuntos de cardinalidad impar, ¿cuál es |A|?.
2.7 Determinar el conjunto potencia de {{},0,{0}}.
2.8 Determinar el conjunto potencia de {0,1,{0,1}}.
2.9 Sean A={1,2,3,5}, B={0,3,5,6}, C={3,4,6,7} y U={0,1,2,3,...,8,9}, Determinar los

elementos de los conjuntos indicados y representar gráficamente la solución.
a) A B.
b) A C.
c) A–B.
d) B–A.
e) A.

f) A B.
g) B C.
h) AxC.
i) A B C
j) B C
k) B A C
2.10 Demuestra lo siguiente:

a) A A B.
b) A B A.
c) Si A B, B C entonces A C.
d) Si C A y C B entonces C A B.
e) Si A C y B C entonces A B C y A B C.
f) Si A B, C D entonces A C B D y A C B D.
g) A B si y solo si A B =∅.
h) A B si y solo si A B =U.
i) A–B C si y sólo si A–C B.
j) (A B) C=A (B C) si y sólo si C A.
k) A=A (A B).
l) A B=(A B) (A B ) ( A B).
m) A=(A B) (A ).
n) A B A B.
o) A B A B.
p) (A–B)–C=(A–C)–(B–C).
q) A B=(A B)–(A B).
r) Si A C=B C y A C=B C entonces A=B.
2.11 Simplifica los conjuntos siguientes usando las leyes del álgebra de conjuntos.
a) (A C ) [A (B C)] (A C)
b) [A (B C)] ( A B ) C
c) (A B) (B A)
d) [B ( C B)] [B (A C)]
e) [(A B ) (A C)] (A B)
f) A (B–A)
g) (A B) [{(A B) ( C D)} ( A B)]
h) (A–B) (A B)
i) ( A B) [(A B) C]
j) (A B) [B {(C D) (C D)}]
k) (A B ) [(A C) (A B)]
l) [(A B) C] [ A ( B C )]

m) (A B) ( A B)]
n) (A B ) (B C) (B C )
o) (A B) (A B ) ( A B) ( A B )
p) [A ( A B )] {[B (B C)] B}
q) (A B) ( A C )
Unidad III: Relaciones
3.1 Definiciones básicas.

3.1.1 Relaciones binarias.
3.1.2 Dominio e Imagen de una relación.
3.1.3 Representación de una relación.
3.1.4 Composición de relaciones.
3.2 Propiedades de las relaciones.

3.2.1 Propiedad Reflexiva.
3.2.2 Propiedad Irreflexiva.
3.2.3 Propiedad Simétrica.
3.2.4 Propiedad Antisimétrica.
3.2.5 Propiedad Transitiva.
3.3 Relaciones de orden.
3.4 Relaciones de equivalencia.

3.4.1 Clases de equivalencia.
3.4.2 El conjunto cociente.
3.5 Funciones.
3.1 DEFINCIONES BÁSICAS
3.1.1 Relaciones binarias
Definición 3.1.1 (Relación)

Una relación R de un conjunto X en un conjunto Y es un subconjunto del producto
cartesiano X Y, es decir, R XxY.

Si (x,y) R se escribe “xRy” y se dice que x está relacionado con y o que x está en relación
con y. En el caso que el conjunto X es igual al conjunto Y, afirmamos que R es una relación
binaria sobre X o sobre Y.
De este modo notamos que una relación queda determinada por cualquier subconjunto del
producto cartesiano.
Ejemplo 3.1.1
Sean los conjuntos X={1,2,3} y Y={1,2}.
El producto cartesiano de X y Y es: X Y={(1,1), (1,2), (2,1), (2,2), (3,1), (3,2)}.
Son relaciones de X en Y las siguientes:
R1={(1,1), (2,1), (3,1)}.
R2={(2,2)}.
R3={(1,1), (1,2), (2,1), (2,2), (3,1), (3,2)}= X Y.
R4= =relación vacía.
Aquí presentamos cuatro relaciones de X en Y, pero ¿cuantas relaciones se podrán

obtener?. En general ¿es posible determinar el número de relaciones que se pueden obtener a
partir de dos conjuntos X y Y?.
Recordando la definición de relación como un subconjunto del producto cartesiano, la

pregunta se puede replantear como ¿cuántos subconjuntos hay del conjunto producto cartesiano?.
Al conjunto de subconjuntos de un conjunto es lo que llamamos conjunto potencia, así hay

que determinar el número de elementos del conjunto potencia del producto cartesiano de X y Y,
esto es, la cardinalidad del conjunto potencia, lo cual nos dará el número de relaciones posibles
de X en Y.
En el ejemplo anterior notamos que la cardinalidad del conjunto producto cartesiano, es

|X Y|=6, luego el número de subconjuntos de X Y es 26=64=23x2=2|X||Y|, es igual a 2 elevado a la
cardinalidad de X por la cardinalidad de Y.
Así en este ejemplo es posible determinar 64 posibles relaciones de X en Y, incluyendo al

producto cartesiano, y la relación que llamamos vacía, determinada por el conjunto vacío 1.
Este resultado nos sugiere la propiedad siguiente.
Propiedad 3.1.1
Para conjuntos finitos X y Y con |X|=m y |Y|=n, existen 2mn relaciones de X en Y,
incluyendo la relación vacía y la propia relación X Y.
También existen 2 nm=2 mn relaciones de Y en X, una de las cuales es también la relación

vacía , y otra es Y X. Esto es porque de cualquier relación R 1 de Y en X puede obtenerse una
única relación R2 de X en Y, invirtiendo simplemente los componentes de cada par ordenado en
R1.
1
Recordemos que el conjunto vacío es subconjunto de cualquier conjunto.

3.1.2 Dominio e Imagen de una relación
Definición 3.1.2 (Dominio de una relación)

Sea R una relación de X en Y, el dominio de la relación R se denotas por DR y se define
como el conjunto de todas las x tales que (x,y) R, es decir:
DR={x | (x,y) R para algún y Y}
Definición 3.1.3 (Imagen de una relación)

Sea R una relación de X en Y, la imagen de la relación R se denota por I R y se define como
el conjunto de todas las y tales que (x,y) R, es decir:
IR={y | (x,y) R para algún x X}
Ejemplo 3.1.2
Sean A={1,2,3} y B={a,b,c}.
Determinar el dominio y la imagen de las relaciones dadas.
a) R1={(1,a), (1,b), (1,c)}.
b) R2={(1,a), (2,b), (3,c)}.
c) R3={(1,a), (2,a), (3,a)}.
Solución
a) DR1={1} IR1={a,b,c}
b) DR2={1,2,3} IR2={a,b,c}
c) DR3={1,2,3} IR3={a}
Para la relación R3, es posible considerar que el contradominio es {a,b,c}. Sin embargo
notemos que el concepto que estamos usando es el de imagen y no el de contradominio ya que
este último contiene a la imagen, tal y como se presenta en cálculo.
3.1.3 Representación de una relación
Una relación se puede representar de diferentes formas, estas son: con el uso de una
condición, un conjunto (tal y como lo presenta la definición), una tabla (idea intuitiva), un dígrafo
y una matriz. La que más usamos es la que se presenta en la definición, esto es como un conjunto.
1. Representación por medio de una condición
Es posible representar a la relación por medio de una condición, en este caso es necesario
conocer donde está definida. En la mayoría de las veces esta representación es, de donde se parte
para el uso de otras representaciones de la relación en donde ya es posible observar todos los
elementos que están en ella.
Ejemplos 3.1.3
a) Consideramos una relación R definida como sigue:

Decimos que x está en relación con y (xRy) si x cursa la asignatura y.

Este enunciado nos presenta la condición que deben cumplir todos los elementos de X y Y
para estar en la relación R.
b) Sean X={1,2,3,4} y Y={1,3,5}

Decimos que x está en relación con y (xRy) si x y y son números primos en XxY.
Los elementos de la relación deben cumplir la condición de que sean primos.
Observe que si la condición debe cumplirse en YxX la relación sería {(3,2), (3,3)}, la cual
es diferente a la que se obtiene en XxY, por eso es importante especificar donde está definida la
relación.
c) Sea X={1,2,3,}.
Decimos que x está en relación con y (xRy) si x + y es par en XxX.
Los elementos de la relación deben cumplir la condición de que su suma sea par.
2. Representación por medio de una tabla
En esta representación se especifican los elementos de x con su y correspondiente.
Ejemplos 3.1.4
Considere las relaciones definidas en el ejemplo 3.1.3.
a) Consideremos que los elementos que están en la relación se presentan en la tabla siguiente:
x cursa la asignatura y
x y El dominio de la relación es:
Benito Computación DR={Benito, María, Carmen, David}
María Matemáticas ={B,M,C,D}.
Benito Artes
Carmen Historia La imagen de la relación es:
Carmen Computación IR={Computación, Matemáticas, Artes,
David Matemáticas Historia}={C,M,A,H}.
Observe que si una relación se representa mediante una tabla, el dominio esta formado por
elementos de la primera columna, y la imagen por los miembros de la segunda.
b)
x y y son números primos
x y
2 3 El dominio de la relación es D R={2,3}.
2 5 La imagen de la relación es I R={3,5}.
3 3
3 5
c)

x + y es un número par
x y
1 1 El dominio de la relación es D R={1,2,3}.
1 3 La imagen de la relación es I R={1,2,3}.
2 2
3 1
3 3
3. Representación por medio de un conjunto
Esta representación queda determinada de la definición de relación, ya que se define a la

relación como un conjunto. Dado que un conjunto se puede representar por extensión o por
compresión, este puede obtenerse por medio de una condición en donde emplearemos la
representación de la relación como una condición y posteriormente como un conjunto, o puede
darse sólo el conjunto que representa a la relación únicamente como un subconjunto del producto
cartesiano.
Ejemplo 3.1.5
Consideremos las relaciones definidas en el ejemplo 3.1.3.
a) R={(B,C), (B,A), (M,M), (C,H), (C,C), (D,M)}.
b) R={(2,3), (2,5), (3,3), (3,5)}.
c) R={(1,1), (1,3), (2,2), (3,1), (3,3)}.
4. Representación por medio de un digrafo
El concepto de dígrafo se desarrollará en una unidad posterior por el momento daremos una
idea gráfica del concepto; un digrafo está formado por puntos y por arcos (líneas con dirección).
Así, un digrafo nos representa una relación si tomamos los elementos de los conjuntos
dominio e imagen como los puntos y la relación entre estos como arcos del digrafo.
Si los conjuntos donde está definida la relación son diferentes se presentan dos columnas de
puntos, estos puntos se unen por medio de líneas con dirección las cuales indican la relación entre
los mismos. Si los conjuntos son iguales (la relación está definida sobre un conjunto) sólo se
presentan una vez los puntos.
El siguiente ejemplo ilustra una relación representada por medio de un digrafo.
Ejemplo 3.1.6
Consideremos las relaciones definidas en el ejemplo 3.1.5.
a) Considere los conjuntos X={B,M,C,D},

Y={C,A,M,H}.
y la relación R definida como:

R={(B,C), (B,A), (M,M), (C,H), (C,C), (D,M)}.

El dígrafo que representa esta relación es:
b) Sean X={1,2,3,4},
Y={1,3,5} y
R={(2,3),(2,5)(3,3)(3,5)}
El digrafo que representa esta relación es
c) Sean X={1,2,3},
R={(1,1), (1,3), (2,2) (3,1), (3,3)}
El dígrafo que representa esta relación es:
Ejemplo 3.1.7.
Sea X={1,2,3} y
R={(1,2), (1,3), (2,2), (3,1)}.
El digrafo que representa la relación es:
5. Representación por medio de una matriz
Para dar la representación de una relación por medio de una matriz empecemos por definir
el concepto.
Definición 3.1.4 (Matriz cero-uno)

Una matriz cero-uno mxn, E=(eij) mxn es una disposición rectangular de números en m filas
y n columnas, donde cada eij, para 1 i m y 1 j n , denota la entrada de la i–ésima fila y la
j-ésima columna de E y cada una de dichas entradas es 0 o 1.
Una matriz es una forma conveniente de representar una relación R de X en Y. Etiquetamos

las filas con los elementos de X y las columnas con los elementos de Y. Entonces colocamos un 1
en el renglón x y la columna y si xRy, y un 0 en caso contrario.
Ejemplo 3.1.8
La matriz
1 0 0 1
E 0 1 0 1 es una matriz 3x4, donde por ejemplo e11=1, e23=0 y e31=1.
1 0 0 0
Ejemplo 3.1.9

Considere la relación definida en los incisos b) del ejemplo 3.1.3.

Sean A={1,2,3,4}, B={1,3,5} y R={(2,3),(2,5)(3,3)(3,5)}.
0 0 0
0 1 1
La matriz de relación es: R=
0 1 1
0 0 0
Ejemplo 3.1.10
a) Considere la relación definida en los incisos c) del ejemplo 3.2.
Sea A={1,2,3} y R={(1,1), (1,3), (2,2) (3,1), (3,3)}.
1 0 1
Matriz de relación, R= 0 1 0
1 0 1
b) Sea R={(1,b), (1,d), (2,c) (3,c), (3,b), (4,a)} de X={1,2,3,4} y Y={a, b, c, d}.
0 1 0 1
0 0 1 0
Matriz de relación, R=
0 1 1 0
1 0 0 0
Ejemplo 3.1.11
La matriz de relación de R={(a,a), (b,b), (c,c), (d,d), (b,c), (c,b)} sobre {a,b,c,d} es
1 0 0 0
0 1 1 0
R=
0 1 1 0
0 0 0 1
Observe que la matriz sobre un conjunto X siempre es una matriz cuadrada.
En el ejemplo siguiente consideraremos una relación y sus distintas formas de

representación.
Ejemplo 3.1.12
Sea X={1,2,3,4} y definimos la relación sobre X como:
1) Representación por condición.
xRy si x<y.
2) Representación por conjunto.

R={(1,2), (1,3), (1,4), (2,3), (2,4), (3,4)}.
3) Representación por Tabla.

X Y
1 2
1 3
1 4
2 3
2 4
3 4
4) Representación por Digrafo.
5) Representación por Matriz.

0 1 1 1
0 0 1 1
R
0 0 0 1
0 0 0 0
Finalmente notemos que el dominio de la relación es {1,2,3} y la imagen es {2,3,4}
Definición 3.1.5 (Relación inversa)

Sea R una relación definida en AxB. La inversa de R, denotada por R -1, es la relación de B
en A definida como
R-1={(y,x) | (x,y) R}
Ejemplo 3.1.13
a) Sean X={1,2,3,4}, Y={1,3,5} y R={(2,3),(2,5)(3,3)(3,5)} definida en XxY.
R-1={(3,2), (5,2), (3,3), (5,3)}.
b) Considere la relación definida en el ejemplo 3.1.12.

xRy si x<y definida en X={1,2,3,4}.
R={(1,2), (1,3), (1,4), (2,3), (2,4), (3,4)}.
R-1={(2,1), (3,1), (4,1), (3,2), (4,2), (4,3)}.
Definición 3.1.6 (Composición de relaciones)
Sea R 1 una relación de X a Y y R2 una relación de Y a Z. La composición de R 1 y R2 ,
denotada por R2  R1, es la relación de X a Z definida por

R2  R1={(x,z) | (x,y) R1 y (y,z) R2 para algún y Y}.
Propiedad 3.1.2
La composición de relaciones es asociativa, esto es
R3  R2  R1=R3  (R2  R1) = (R3  R2)  R1
Ejemplo 3.1.14
a) Sean R1 y R2 relaciones sobre X={1,2,3,4} dadas por:
R1={(1,1),(1,2),(3,4),(4,2)}.
R2={(1,1),(2,1),(3,1),(4,4),(2,2)}.
R2  R1 = {(1,1), (1,2), (3,4), (4,1), (4,2)}.
R1  R2 = {(1,1), (1,2), (2,1), (2,2), (3,1), (3,2), (4,2)}.
b) Sean X={1,2,3}, Y={2,4,6,8}, Z={u,s,t} y R1 , R2 relaciones definidas en XxY y YxZ

respectivamente como
R1={(1,2),(1,6),(2,4),(3,4),(3,6),(3,8)} y R 2={(2,u),(4,s),(4,t),(6,t),(8,u)}.
R2  R1={(1,u),(1,t),(2,s),(2,t),(3,s),(3,t),(3,u)} es una relación definida en XxZ.
Definición 3.1.7 (Potencia de una relación)

Dado un conjunto X una relación R sobre X, definimos la potencia de R de manera
recursiva como
1. R1=R
2. para n Z+, R n+1=R n  R
Es decir, R2=R  R, R 3=R2  R=R  R  R, R4=R3  R=R  R  R  R, etc.
Ejemplo 3.1.15
Considere las siguientes relaciones definidas sobre X={a,b,c}.
a) R1={(a,b), (a,c), (c,b)}.
R12 ={(a,b)}.
R13 R14 ...
b) R2={(a,b), (b,c), (c,a)}.

R22 ={(a,c), (b,a), (c,b)}.
R23 ={(a,a), (b,b), (c,c)}.

R24 R2 , R25 R24 , R26 R23 .
c) R3={(a,b), (b,c), (c,c)}.

R32 ={(a,c), (b,c), (c,c)}= R33 R34 R35 ...
d) R4={(a,b), (b,a), (c,c)}.
R42 ={(a,a), (b.b), (c,c)=.

R43 R4 , R44 R42 .
Es posible decir que cuando mucho hay n potencias distintas de R. R m, m>n, se puede
expresar con base en R, R2 ,…,R n.
Ahora bien podemos definir R + como R R R2 R3 ...
Ejemplo 3.1.16
Considere las relaciones definidas en el ejemplo 3.1.15.
a) R1 R1 R12 R13 ... R1 = {(a,b), (a,c), (c,b)}
b) R2 R2 R22 R23 ... R2 R22 R23 =
{(a,b),(b,c),(c,a),(a,c),(b,a),(c,b),(a,a),(b,b),(c,c)}
c) R3 R3 R32 R33 ... R3 R32 ={(a,b), (b,c), (c,c), (a,c)}
d) R4 R4 R42 R43 ... R4 R42 ={(a,b), (b,a), (c,c), (a,a), (b,b)}
Observe que R1 R1 , R2 R2 , R3 R3 y R4 R4 .
Ejemplo 3.1.17
Sean R = {(1,2),(3,4),(2,2) y S = {(4,2),(2,5),(3,1),(1,3)}
Encuentre: R°S, S°R, R°(S°R), (R°S)°R, R°R, S°S y R°R°R.
Solución
R°S={(1,5),(3,2),(2,5)}.
S°R={(4,2),(3,2),(1,4)}.
(R°S)°R={(3,2)}.
R°(S°R)={(3,2)}.
R°R={(1,2),(2,2)}.
S°S={(4,5),(3,3),(1,1)}.
R°R°R={(1,2), (2,2)}.
Como las relaciones son conjuntos, cumplen las mismas propiedades y definiciones que
estos. El siguiente teorema puede demostrarse basándose en las definiciones y propiedades de los
conjuntos.
Teorema 3.1.1
Supóngase que R y S son relaciones de A en B

a) Si R S R 1 S 1.
b) Si R S S R.
c) R S 1 R 1 S 1.
d) R S 1 R 1 S 1.
e) R S S R.
f) R S S R.
3.6 PROPIEDADES DE LAS RELACIONES
A partir de este tema nos centraremos en las relaciones definidas sobre un conjunto.
3.2.1 Propiedad Reflexiva
Definición 3.2.1 (Relación reflexiva)

Una relación R sobre un conjunto X, es reflexiva si (x,x) R para toda x X. Esto equivale
a decir: R es reflexiva si todo elemento de x esta relacionado con si mismo.
x X (x,x) R
Ejemplo 3.2.1
a) La relación de contención entre conjuntos es reflexiva por que todo conjunto esta contenido
en si mismo.
b) Si X es el conjunto de todas las rectas del plano, la relación de paralelismo entre rectas es
reflexiva por que toda recta es paralela a si misma.
3.2.2 Propiedad Irreflexiva.
Definición 3.2.2 (Relación irreflexiva)

Una relación R sobre un conjunto X, es irreflexiva si (x,x) R para toda x X. Esto equivale
a decir: R es irreflexiva si ningún elemento de x esta relacionado con si mismo.
x X (x,x) R
Ejemplo 3.2.2
Si X es el conjunto de todas las rectas del plano, la relación de perpendicularidad entre 2
rectas es irreflexiva, ya que no hay rectas que sean perpendiculares a sí mismas.
3.2.3 Propiedad simétrica
Definición 3.2.3 (Relación simétrica)

Una relación R sobre un conjunto X, es simétrica si para todo (x,y) R se tiene que (y,x) R.
Esto equivale a decir: R es simétrica si y sólo si para todo par de la relación, también se encuentra
el par conmutado en la relación.
x,y X (x,y) R (y,x) R
Ejemplo 3.2.3
a) Si X es el conjunto de todos los seres humanos, la relación: “ser hermano de” es simétrica.
b) Si X es el conjunto de todos los seres humanos, la relación “ser mas alto que” no es
simétrica.
c) Si X es el conjunto de todas las rectas del plano, las relaciones de paralelismo y

perpendicularidad entre 2 rectas son relaciones simétricas.
3.2.4 Propiedad antisimátrica
Definición 3.2.4 (Relación antisimétrica)

Una relación R sobre un conjunto X, es antisimétrica si para todo (x,y) R con x y se tiene
que (y,x) R. Esto equivale a decir: R es antisimétrica si y sólo si para todo par diferente de la
relación, el par conmutado no se encuentra en la relación.
x,y X (x,y) R con x y (y,x) R
Ejemplo 3.2.4
a) La relación de contención de conjuntos es antisimétrica por que dados dos conjuntos A, B
donde A B, si A B entonces B A.
b) En el conjunto de todos los seres humanos la relación “ser tío de” es antisimétrica.
3.2.5 Propiedad transitiva
Definición 3.2.5 (Relación transitiva)

Una relación R sobre un conjunto X, es transitiva si para todo (x,y) R y (y,z) R se tiene
que (x,z) R. Esto equivale a decir que R es transitiva, si y sólo si dados dos pares de la relación
tales que la segunda coordenada del primer par es igual a la primera coordenada del segundo par,
el par ordenado formado por la primera coordenada del primer par y la segunda coordenada del
segundo par está en la relación.
x,y,z X ((x,y) R y (y,z) R) (x,z) R.
Ejemplo 3.2.5
a) La contención de conjuntos es transitiva, esto es, para los conjuntos A, B y C, se cumple
que si A B y B C entonces A C.

b) Si A es el conjunto de todas las rectas del plano, la relación de perpendicularidad entre dos
rectas no es transitiva, porque si l1 l2 y l2 l3 entonces l1 l3.
c) Si A es el conjunto de todas las rectas del plano, la relación de paralelismo entre dos rectas
es transitiva, porque si l1 || l2 y l2 || l3 entonces l1 || l3 .
Estas propiedades pueden también identificarse con las representaciones de una relación como
digrafo o matriz, solo que estas no son muy precisas. Así, tenemos:
Propiedad Definición Matriz Digrafo

Reflexiva x X (x, x) R La diagonal principal está Todos los vértices tienen
formada sólo por unos. lazos
Irreflexiva x X (x, x) R La diagonal principal esta Ningún vértice tiene lazos.
formada sólo por ceros.
Simétrica x, y X Los elementos de la matriz Todos los vértices asociados
(x,y) R (y,x) R son “simétricos” con tienen dos flechas.
respecto a la diagonal
principal, esto es, se
reflejan.
Antisimétrica x, y X Ningún uno se refleja con Todos los vértices asociados
(x,y) R con x y respecto a la diagonal tienen solo una flecha.
(y, x) R principal.
Transitiva x, y, z X No es posible determinar No es posible determinar
((x,y) R y (y,z) R) fácilmente esta propiedad fácilmente esta propiedad
(x, z) R. con esta representación. con esta representación.
Ejemplo 3.2.6
a) Determinar las propiedades que cumple la relación definida sobre X={1,2,3,4} como xRy si
x<y.
Solución
La relación es R={(1,2), (1,3), (1,4), (2,3), (2,4), (3,4)}, las propiedades que cumple son:
1) No es reflexiva, porque 1 X y (1,1) X.
2) Es irreflexiva, porque 1 X y (1,1) X, 2 X y (2, 2) X, 3 X y (3,3) X, 4 X y (4,4) X
y 5 X y (5,5) X.
3) No es simétrica, porque (1,2) X y (2,1) X.
4) Es antisimétrica, porque (1,2) X y (2,1) X, (1,3) X y (3,1) X, (1,4) X y (4,1) X,
(2,3) X y (3,2) X, (2,4) X y (4,2) X y (3, 4) X y (4,3) X.
5) Es transitiva, porque (1,2) y (2,3) X y (1,3) X.
(1,2) y (2,4) X y (1,4) X
(1,3) y (3,4) X y (1,4) X
(1,3) y (3,4) X y (1,4) X

0 1 1 1
0 0 1 1
Usando la matriz R tenemos:
0 0 0 1
0 0 0 0
1) No es reflexiva, no hay sólo 1’s en la diagonal principal.

2) Es irreflexiva, hay solo 0’s en la diagonal principal.
3) No es simétrica no se refleja la matriz con respecto al a diagonal principal.
4) Es antisimétrica ningún elemento de la matriz se refleja con respecto a la diagonal

principal.
5) No se puede determinar la transitividad con esta representación.
Usando el dígrafo tenemos:

1) No es reflexiva, no hay lazos en todos los vértices.
2) Es irreflexiva, ningún vértice tiene lazo.
3) No es simétrica, no hay dos flechas asociadas a cada par de
vértices que están en relación.
4) Es antisimétrica, todos los vértices relacionados tiene
asociada solo una flecha.
5) No se puede determinar la transitividad con esta
representación.
Así, con cualquier representación que se use obtenemos que R no es reflexiva, es irreflexiva, no
es simétrica, es antisimétrica y es transitiva.
b) CASO ESPECIAL
La relación llamada identidad definida sobre X={1,2,3,4,5} definida por xRy si x=y.
Así R={(1,1), (2,2), (3,3), (4,4), (5,5)}.
Esta relación es reflexiva, simétrica, antisimétrica y transitiva.
Teorema 3.2.1
Sea R una relación sobre un conjunto A.
a) Si R es reflexiva entonces R-1 es reflexiva.
b) R es reflexiva si y sólo si R es irreflexiva.
(NOTA: Una relación R es irreflexiva si y sólo si R I= , donde I es la relación identidad).
c) R es simétrica si y sólo si R=R -1.
d) Si R es simétrica entonces R -1 es simétrica.
e) Si R es simétrica entonces R es simétrica.
f) R es antisimétrica si y sólo si R R-1 I.
g) R es asimétrica si y sólo si R R-1= .
h) Si R es antisimétrica entonces R -1 es antisimétrica.

Ejemplo 3.2.7
Demuestre que si R y S son relaciones simétricas entonces R S es simétrica.
Demostración 1:
Sea (x,y) (R S) Por lo que se tiene que (x,y) R (x,y) S
Como R y S son simétricas se tiene que
(y,x) R (y,x) S en consecuencia (x,y) (R S), por lo tanto R S es simétrica.
Demostración 2
Como R y S son simétricas, por el teorema 3.2.1 c), se tiene que R=R -1 y S=S-1.
R S=R -1 S-1=(R S)-1 por teorema 3.1.1 d).
En consecuencia R S es simétrica.
Ejemplo 3.2.8
Demuestre que si R y S son relaciones transitivas entonces R S es transitiva.
Demostración:
Por demostrar que si (x,y) (R S) y (y,z) (R S) entonces (x,z) (R S).
Sean (x,y) (R S) y (y,z) (R S) de esto se tiene que
((x,y) R (x,y) S) ((y,z) R (y,z) S) asociando se tiene que
((x,y) R (y,z) R) ((x,y) S (y,z) S), Dado que R y S son transitivas se tiene que
((x,z) R (x,z) S) es decir, (x,z) (R S), en consecuencia R S es transitiva.
3.3 RELACIÓN DE ORDEN
De acuerdo a las propiedades que cumplen las relaciones es posible clasificarlas en

relaciones de orden o de equivalencia, empezaremos considerando las relaciones de orden, las
cuales se definen a continuación.
Definición 3.3.1 (Relación de orden)

Sea A un conjunto y R una relación binaria definida en A. Diremos que la relación R es una
relación de orden si y sólo si R es
a) Antisimétrica y transitiva, ó
b) Irreflexiva, Antisimétrica y transitiva.
Definición 3.3.2 (Relación de orden parcial)

Sea A un conjunto y R una relación sobre A. Diremos que R es una relación de orden
parcial, si y sólo si R es de orden y reflexiva, esto es, R es reflexiva, transitiva y antisimétrica.
Definición 3.3.3 (Ley de tricotomía)

Sea A un conjunto y R una relación sobre A. Diremos que la relación R satisface en A la

Ley de Tricotomía si y sólo si de forma excluyente se tiene:
x=y ó (x,y) R ó (y,x) R
Observación: De acuerdo a las condiciones que se presentan para que se cumpla la ley de
tricotomía nos damos cuenta que:
1) Las relaciones simétricas no cumplen la ley de tricotomía.

2) Si la relación tienen pares ordenados con misma coordenada, esto es, (x,x) R; entonces la
relación no cumple la ley de tricotomía.
Definición 3.3.4 (Relación de orden total)

Sea A un conjunto y R una relación sobre A. Diremos que R es una relación de orden
total, si y sólo si R es de orden y satisface la ley de tricotomía, esto es, R es antisimétrica,
transitiva y tricotomía.
Definición 3.3.5 (Relación de cuasiorden)

Sea A un conjunto y R una relación sobre A. Diremos que R es una relación de cuasiorden,
si y sólo si R es reflexiva y transitiva.

Ejemplo 3.3.1
Consideremos el siguiente organigrama de una escuela:
Director a
b Subdirector Subdirector
Académico Administrativo c
Jefe Dpto 1 Jeje Dpto 2 Jefe Dpto 3 Jefe Dpto 4
d e f g
La relación R, definida por x depende de y, es
R={(b,a),(c,a),(d,b),(e,b),(d,a),(e,a),(f,c),(g,c),(f,a),(g,a)}
Determine las propiedades que cumple la relación.
Solución
R no es reflexiva, no hay pares de la forma (x,x) en R.
R es irreflexiva, no hay pares de la forma (x,x) en R.
R no es simétrica, (b,a) R y (a,b) R.
R es antisimétrica, (b,a) R y (a,b) R. (c,a) R y (a,c) R.
(d,b) R y (b,d) R. (e,b) R y (b,e) R.
(d,a) R y (a,d) R (e,a) R y (a,e) R.
(f,c) R y (c,f) R. (g,c) R y (c,g) R.
(f,a) R y (a,f) R. (g,a) R y (a,g) R.
R es transitiva (d,b) y (b,a) R (d,a) R (e,b) y (b,a) R (e,a) R

(f,c) y (c,a) R (f, a) R (g,c) y (c,a) R (g,a) R
Así, R es irreflexiva, antisimétrica y transitiva. Por lo tanto R es una relación de orden.
Ejemplo 3.3.2
a) Sea A={a,b,c} y R la relación definida sobre A, del modo siguiente:
R={(b,a), (c,b), (c,a)}
Determine las propiedades de la relación.
Solución
R no es reflexiva no hay pares de la forma (x,x) en R.
R es irreflexiva no hay pares de la forma (x,x) en R.
R no es simétrica (b,a) R y (a,b) R.
R es antisimétrica, (b,a) R y (a,b) R.
(c,b) R y (b,c) R.
(c,a) R y (a,c) R.

R es transitiva (c,b) y (b,a) R (c,a) R.
R cumple la ley Para a y b sólo se cumple (b,a) R, en la relación notamos que (b,a) R
de tricotomía y notamos que a b, este mismo análisis se tiene para los otros elementos.
Como R es antisimétrica,, transitiva y cumple la ley de tricotomía es una relación de orden

total.
Si la relación cumple irreflexiva y antisimétrica entonces es asimétrica, esta propiedad esta

implícita en las otras dos propiedades.
b) Sea A={a,b,c} y R la relación definida sobre A del modo siguiente

R={(a,a), (b,b),(c,c), (a,c), (b,c), (c,b), (a,b)}
Determinemos las propiedades que cumple la relación.
Solución
R es reflexiva, (a,a), (b,b) y (c,c) R.
R no es irreflexiva (a,a) R.
R no es simétrica (a,c) R y (c,a) R.
R no es antisimétrica (b,c) R y (c,b) R.
R es transitiva (a,c) y (c,b) R (a,b) R.
(b,c) y (c,b) R (b,b) R.
(c,b) y (b,c) R (c,c) R.
(a,b) y (b,c) R (a,c) R.
Como R es una relación reflexiva y transitiva es una relación de cuasiorden.
c) Sea A={a,b,c} y R la relación definida sobre A tal que

R={(a,a), (b,b), (c,c), (a,c), (c,b), (a,b)}
Solución
R es reflexiva, (a,a), (b,b) y (c,c) R.
R no es irreflexiva (a,a) R.
R no es simétrica (a,c) R y (c,a) R.
R es antisimétrica (a,c) R y (c,a) R.
(c,b) R y (b,c) R.
(a,b) R y (b,a) R.
R es transitiva (a,c) y (c,b) R (a,b) R.
Como R es reflexiva, antisimétrica y transitiva., R es una relación de orden parcial.

3.4 RELACIONES DE EQUIVALENCIA
Definición 3.4.1 (Relación de equivalencia)

Sea A un conjunto y R una relación definida sobre A. Diremos que R es una relación de
equivalencia si y sólo si R es reflexiva, simétrica y transitiva; es decir, si R cumple las
condiciones.siguientes:
i) (x,x) R x A.
ii) Si (x,y) R entonces (y,x) R.
iii) Si (x,y) R y (y,z) R, entonces (x,z) R.
Ejemplo 3.4.1
a) Sea A=conjunto de todos los triángulos y R la relación en A determinada por la semejanza
de triángulos, esto es, si t1 y t2 son triángulos en A, entonces (t1, t2) R si y sólo si t1 es
semejante a t2. Determine las propiedades que cumple la relación.
Solución
Recordemos que dos triángulos son semejantes, si:
Los 3 lados son proporcionales.
Dos lados son proporcionales y el ángulo que sustentan igual.
Los tres ángulos son iguales.
R es reflexiva, por que los ángulos de t 1 son iguales a los ángulos de t1.
R no es ireflexiva, porque los ángulos de t1 son iguales a los ángulos de t1 .
R es simétrica, por que si los ángulos del triángulo t1 son iguales a los ángulos del
triángulo t2 , entonces los ángulos del triángulo t2 son iguales a los
ángulos del triángulo t1.
R no es antisimétrica, por que si los ángulos del triángulo t1 son iguales a los ángulos del
triángulo t2 , entonces los ángulos del triángulo t2 son iguales a los
ángulos del triángulo t1.
R es transitiva, porque si los ángulos del triángulo t1 son iguales a los ángulos del
triángulo t2, y si los ángulos del triángulo t2 son iguales a los
ángulos del triángulo t3, entonces los ángulos del triángulo t1 son
iguales a los ángulos del triángulo t3 .
Como R es reflexiva, simétrica y transitiva, R es una relación es de equivalencia.
b) Sea R={(1,1), (1,3), (1,5), (2,2), (2,4), (3,1), (3,3), (3,5), (4,2), (4,4), (5,1), (5,3), (5,5)}
definida sobre X={1,2,3,4,5}.
Solución
R es reflexiva, por que (1,1), (2,2), (3,3), (4,4), (5,5) R.
R no es irreflexiva, porque (1,1) R.
R es simétrica, porque (1,3) R y (3,1) R, (1,5) R y (5,1) R.
(2,4) R y (4,2) R (3,1) R y (1,3) R.
(3,5) R y (5,3) R (4,2) R y (2,4) R.
(5,1) R y (1, 5) R (5,3) R y (3,5) R.

R no es simétrica, por que (1,3) R y (3,1) R.

R es transitiva, porque (1,3) R y (3,1) R (1,1) R.
(1,3) R y (3,5) R (1,5) R.
(1,5) R y (5,1) R (1,1) R.
(1,5) R y (5,3) R (1,3) R.
(2,4) R y (4,2) R (2,2) R.
(3,1) R y (1,3) R (3,3) R.
(3,1) R y (1,5) R (3,5) R.
(3,5) R y (5,1) R (3,1) R.
(3,5) R y (5,3) R (3,3) R.
(4,2) R y (2,4) R (4,4) R.
(5,1) R y (1,3) R (5,3) R.
(5,1) R y (1,5) R (5,5) R.
(5,3) R y (3,1) R (5,1) R.
(5,3) R y (3,5) R (5,5) R.
Como la relación es reflexiva, simétrica y transitiva, R es una relación de equivalencia.
Ejemplo 3.4.2
a) Sea el conjunto A={a,b,c,d,e} y R=Ax(A-{a}), Determinar si R es: reflexiva, simétrica,
asimétrica, antisimétrica, transitiva, de equivalencia, de orden parcial o de orden total.
Solución
R no es reflexiva, a A y (a,a) R.
R no es simétrica, (a,b) R y (b,a) R.
R no es asimétrica, (b,c) R y (c,b) R.
R no es antisimétrica, (b,c) R y (c,b) R pero b c.
R es transitiva, si (a,b) R y (b,c) se tiene que (a,c) R.
R no es de equivalencia, R no es reflexiva ni es simétrica.
R no es de orden parcial, R no es reflexiva.
La relación no es de orden parcial R no es reflexiva ni antisimétrica.
b) Sea el conjunto A={1,2,3,4,5,6,7,8,9}, P(a) el conjunto potencia de A, y R la relación

definida en P(A)xP(A) dada por R={(x,y)| x y }. Determine si R es reflexiva, simétrica,
asimétrica, antisimétrica, transitiva, de equivalencia, de orden parcial o de orden total.
Solución
R no es reflexiva, P(A) y = .
R es simétrica, la intersección de conjuntos es conmutativa así, si x y entonces,
y x .
R no es asimétrica, por que es simétrica.
R no es antisimétrica, por que si x y se tiene que y x y x y.
R no es transitiva, por que si x y yy z no implica que x z .
Contraejemplo: sean x={1,2,3}, y={2,3,4,5} y z={5,6,7}
x y={2,3} , y z={5} pero x z , de lo anterior se concluye

que (x,y) R, (x,z) R pero (x,z) R.

De lo anterior concluimos que:

R no es de equivalencia por que no es reflexiva ni transitiva.
R no es de orden parcial por que R no es transitiva, no es reflexiva y no es antisimétrica.
R no es de orden total por que no es reflexiva ni transitiva.
R no es de cuasiorden por que no es reflexiva ni transitiva.
Ejemplo 3.4.3
a) Determinar las propiedades que cumple la relación.
R={(x,y)|3 divide a x–y}
Definida sobre el conjunto de los enteros.
Solución
Reflexiva.
La relación es reflexiva, si para todo x entero se cumple que (x,x) R.
Por la definición de la relación (x,x) R, si 3 divide a x–x.
Por la definición de divisibilidad 3|x–x si existe q Z tal que x–x=3q.
Como x–x=0, entonces 0=3q y el entero que cumple con esta condición es 0.
Así 3|x–x y (x,x) R.
Por lo tanto, la relación R es reflexiva.
Irreflexiva
La relación es irreflexiva, si se cumple que (x,x) R.
Sin embargo mostramos que (x,x) R para todo número entero.
Por lo tanto, la relación no es irreflexiva.
Simétrica
La relación es simétrica, si para todo (x,y) R se cumple (y,x) R.
Lo que nos señala que hay que mostrar que la proposición condicional es válida.
Por hipótesis se tiene que (x,y) R, lo que implica que 3|x–y, esto es, que existe un entero q1
tal que x–y=3q1.
Hay que mostrar que (y,x) R, esto es, que existe un entero q tal que y–x=3q.
Ahora bien y–x=–(x–y)=–3q1=3(–q1)
Así es posible representar a y–x como el producto de 3 y de –q1 , y este es el entero que se
buscaba.
Por lo tanto, la relación es simétrica.
Antisimétrica
La relación es antisimétrica, si para todo (x,y) R con x≠y se cumple que (y,x) R.
La proposición condicional, tiene por hipótesis (x,y) R, lo que implica que 3|x–y, esto es,
existe un entero q1 ≠0 tal que x–y=3q1.
Hay que mostrar (y,x) R, esto es, que no existe un entero q tal que y–x=3q o, de manera
equivalente que y–x=3q donde q Z.
Se tiene que, y–x=–(x–y)=–3q1=3(–q1) y –q1 Z, por lo tanto no se cumple la proposición

condicional y la relación no es antisimétrica.

Transitiva
La relación es transitiva, si para todo (x,y) R y para todo (y,z) R se cumple (x,z) R.
Por hipótesis se tiene que (x,y) R y (y,z) R lo que implica que 3|x–y,3|y–z esto es, que
existen enteros q1 y q2 tales que x–y=3q1 y y–z =3q2 .
Se debe mostrar que (x,z) R, esto es, que existe un entero q tal que x–z=3q.
Sumando las dos igualdades de la hipótesis, se tiene:
(x–y)+(y–z)=3q1 + 3q2
x–z=3(q1+q2)
así, es posible representar a x–z como el producto de 3 y de un número entero q=q1+q2,
(q1+q2 es entero porque tanto q1 como q2 lo son)
Por lo tanto, la relación es transitiva.
Ley de Tricotomía
La relación no cumple la ley de tricotomía, porque para x y x en Z, se tiene que x=x y que
(x,x) R; cumpliéndose más de una de las condiciones para la ley de tricotomía.

R es de equivalencia por que es reflexiva, simétrica y transitiva.
R no es de orden por que no es antisimétrica.
R no es de orden parcial por que no es antisimétrica.
R no es de orden total no cumple la ley de tricotomia.
R es de cuasiorden por que es reflexiva y transitiva.
b) Determinar las propiedades que cumple la relación R={(x,y)|x y}, definida sobre el
conjunto de los enteros.
Solución
Reflexiva.
Por la definición de la relación (x,x) R, si x x, como x=x, se cumple la igualdad y (x,x) R.
Irreflexiva
Simétrica
Lo que nos señala que hay que mostrar que la proposición condicional es válida.
Tiene por hipótesis (x,y) R, lo que implica que x y.
Hay que mostrar (y,x) R, esto es, que y x.
Por hipótesis x y, así x no es mayor que y y (y,x) R

Por lo tanto, la relación no es simétrica.

Antisimétrica
La relación es antisimétrica, si para todo (x,y) R con x≠y se cumple que (y,x) R
Tiene por hipótesis (x,y) R, lo que implica que x<y.
Hay que mostrar (y,x) R, esto es, que y<x.
Por hipótesis x<y, así x no es mayor que y y (y, x) R.
Por lo tanto, la relación es antisimétrica.
Transitiva
La relación es transitiva, si para todo (x,y) R y para todo (y,z) R se cumple (x,z) R.
Por hipótesis se tiene que Hipótesis (x,y) R y (y,z) R lo que implica que x y y y z.
Se debe mostrar que (x,z) R, esto es, x z.
Se tiene que x y z por lo tanto x z.
Por lo tanto la relación es transitiva.
Ley de Tricotomía
La relación no cumple la ley de tricotomía, porque para x y x en Z, se tiene que x=x y

R no es de equivalencia por que no es simétrica.
R es de orden por que es transitiva y antisimétrica.
R es de orden parcial por que es reflexiva, transitiva y antisimétrica.
R no es de orden total no cumple la ley de tricotomía.
R es de cuasiorden por que es reflexiva y transitiva.
c) Determinar las propiedades que cumple la relación

R={(x,y)| x y 2 }
Definida sobre el conjunto de los enteros.
Solución
Reflexiva.
Por la definición de la relación (x,x) R, si x y 2 .
x x 0 2 , así (x,x) R.
Irreflexiva
Simétrica
Hipótesis (x,y) R, lo que implica que x y 2

Hay que mostrar (y,x) R, esto es y x 2.

y x x y ( 1)( x y) 1x y x y 2.
luego (y,x) R. or lo tanto, la relación es simétrica.
Antisimétrica
La relación es antisimétrica, si para todo (x,y) R con x≠y se cumple que (y,x) R.
Hipótesis (x,y) R, lo que implica que x y 2
Hay que mostrar (y,x) R, esto es, que y x 2 o, de manera equivalente que y x 2,
sin embargo encontramos que y x 2 ; por lo que (y, x) R.
Por lo tanto, la relación no es antisimétrica.
Transitiva
La relación es transitiva, si para todo (x, y) R y para todo (y, z) R se cumple (x, z) R.
Hipótesis (x,y) R y (y, z) R, lo que implica que x y 2 y y z 2
Hay que mostrar que (x, z) R, esto es, que x z 2.
x z x y y z ( x y) ( y z ) x y y z 2 2 4.
Luego, x z 4 y (x, z) R.
Por lo tanto, la relación no es transitiva.
Ley de Tricotomía
La relación no cumple la ley de tricotomía, porque para x y x en Z, se tiene que x=x y que

R no es de equivalencia por que no es transitiva.
R no es de orden por que no es ni transitiva ni antisimétrica.
R no es de orden total por que no es transitiva y no cumple la ley de tricotomía.
R no es de cuasiorden por que no es transitiva.
Partición de un conjunto
De alguna manera estamos familiarizados con el concepto de partición. En anatomía por

ejemplo se puede hacer una partición del cuerpo humano en: cabeza, tronco y extremidades. La
división de un país en estados, etc. En matemáticas se usa también este concepto asociado con las
relaciones de equivalencia.
Para introducir el concepto consideremos la partición de una casa, está se puede dividir en:
sala, comedor, cocina, recamara y baño; cada una de las partes de la casa no es vacía no vamos a
decir que se considera un cuarto que no exista, ninguna de las partes de la casa tiene un fin
diferente lo que señala que no son iguales; y finalmente si juntamos todas las partes de la casa lo

que se obtiene es precisamente una casa, no algo menos o más. Este ejemplo nos muestra las
condiciones que se debe tener el conjunto para poder tener lo que llamamos partición, veamos la
definición del concepto.
Definición 3.4.2 (Partición de un conjunto)

Sea X un conjunto y L(X) un conjunto de subconjuntos de X (que no es el conjunto
potencia de X). Diremos que L(X) es una partición del conjunto X si y sólo si se cumple las
siguientes propiedades:
i) El conjunto vacío no pertenece a L(X); simbólicamente L(X).
ii) Todos los elementos de L(X) son ajenos entre sí; en forma simbólica Ai Aj= , para i≠j y
Ai, Aj L(X).
iii) La unión de todos los elementos de L(A) es igual a A; simbólicamente A= Ai.
Ejemplo 3.4.4
a) Sea X={1,2,3,4,5,6,7,8,9,10}.
Una partición de X es L(X)={A1,A2} donde A1={1,3,5,7,9} y A2={2,4,6,8,10}
Puede verse que:
i) A1 ≠ ; A2 ≠ .
ii)A1 A2= .
iii)A1 A2=A.
Otra partición de X es
L2(X)={A1,A2 ,A3,A4}.
Donde A1={2,3}, A2={3,4,5}, A3={6,7,8,9}, y A4={10}.
Es posible verificar que se cumplen las condiciones de la definición.
Finalmente otra partición de X la constituye el mismo conjunto X, esto es:

L3(X)={X}.
b) Dado el conjunto X={1,2,3,4,5,6}, se tiene la partición L(X)={A1,A2,A3}

donde A1={1,3,5}, A2={2,6} y A3={4}. Es una partición porque:
i) A1={1,3,5}≠ .
A2={2,6}≠ .
A3={4}≠ .
ii)A1 A2= , A1 A3= y A2 A3= .
iii)A1 A2 A3={1,2,3,4,5,6}=X.
El siguiente teorema muestra como utilizar una partición para definir una relación de
equivalencia.
Teorema 3.4.1
Sea L(X) una partición del conjunto X. Defínase xRy si x y y pertenecen a Ai para algún
Ai L(X). Entonces R es reflexiva, simétrica y transitiva.

Demostración
Reflexiva
Sea x X. Como X= Ai, x Ai para algún Ai L(X). Entonces xRx y R es reflexiva.
Simétrica
Supóngase que xRy. Entonces x y y pertenecen a algún conjunto Ai L(X). Como x y y
pertenecen a Ai, yRx y R es simétrica.
Transitiva
Supóngase que xRy y yRz. Entonces x y y pertenecen a un conjunto Ai L(X); asimismo, y
y z pertenecen a un conjunto Aj L(X). Si Ai Aj, se tiene que y pertenecería a Ai y a Al;
pero como L(X) es una familia disjunta por pares, esto es imposible. Entonces A i=Ajy tanto
x como z pertenecen a Ai. Por lo tanto xRz y R es transitiva.
Ejemplo 3.4.5
a) Considérese la partición L={{1,3,5},{2,6},{4}} de X={1,2,3,4,5,6}.
Determine la relación R sobre X.
Solución
R={(1,1),(1,3),(1,5),(3,1),(3,3),(3,5),(5,1),(5,3),(5,5),(2,2),(2,6),(6,2),(6,6),(4,4)}.
b) Dado el conjunto X={1,3,5,7,9} y la partición L(X)={{1,3}, {5}, {7,9}}, determine la

relación de equivalencia que corresponda a esta partición.
Solución
R={(1,1),(1,3),(3,1),(3,3),(5,5),(7,7),(7,9)(9,7),(9,9)}.
Sean L(X) y R como en el teorema anterior. Si Ai L(X) es posible considerar los

elementos de Ai como equivalentes en el sentido de la relación R. Por esta razón, las relaciones
que son reflexivas, simétricas y transitivas se llaman relaciones de equivalencia.
3.4.3 Clases de equivalencia
Definición 3.4.3 (Clases de equivalencia)

Sea R una relación de equivalencia en un conjunto X. Los conjuntos
[a]={x X│xRa o (x,a) R} se denominan clases de equivalencia de X inducidas por la relación
R.
Ejemplo 3.4.6
a) Consideremos la relación de equivalencia
R (1,1),(1,3),(1,5),(2, 2),(2,6),(3,1),(3,3),(3,5),(4, 4),(5,1),(5,3),(5,5),(6, 2),(6,6)

definida sobre X={1,2,3,4,5,6}
Las clases de equivalencia son:
[1]={1,3,5}.
[2]={2,6}.
[3]={1,3,5}.
[4]={4}.
[5]={1,3,5}.

[6]={2,6}.
Observemos que hay clases de equivalencia iguales
[1]=[3]=[5]
[2]=[6]
y que precisamente son iguales las clases de los elementos que la conforman. Así
observamos que [1]={1, 3, 5} y [1]=[3] =[5].
b) Consideremos la relación de equivalencia

R={(1,1), (1,3), (1,5), (2,2), (2,4), (3,1), (3,3), (3,5), (4,2), (4,4), (5,1), (5,3), (5,5)}
Sobre X={1,2,3,4,5}
Las clases de equivalencias son:
[1]={1,3,5}.
[2]={2,4}.
[3]={1,3,5}.
[4]={2,4}.
[5]={1,3,5}.
c) Sea X={1,2,3,4,5,6,7,8,9,10}. Defínase xRy si 3 divide a 3–y. Esta es una relación de

equivalencia, (puede verificarse).
Clase de equivalencia:
[1] esta formada por todos los x tales que xR1, así
[1]={x X|3 divide a x–1}={1,4,7,10}.
[2]={x X|3 divide a x–2}={2,5,8}.
[3]={x X|3 divide a x–3}={3,6,9}.
[4]={x X|3 divide a x–4}={1,4,7,10}.
[5]={x X|3 divide a x–5}={2,5,8}.
[6]={x X|3 divide a x–6}={3,6,9}.
[7]={x X|3 divide a x–7}={1,4,7,10}.
[8]={x X|3 divide x–8}={2,5,8}.
[9]={x X|3 divide a x–9}={3,6,9}.
[10]={x X|3 divide a x–10}={1,4,7,10}.
En donde se tiene que:
[1]=[4]=[7]=[10].
[2]=[5]=[8].
[3]=[6]=[9].
La relación de equivalencia que consideramos es semejante a plantear, están en la relación

las diferencias que tienen el mismo residuo cuando se divide entre 3.
Ejemplo 3.4.7
Sea A un conjunto cualquiera y sea R la relación de igualdad definida en A. Para cualquier
x A la clase de equivalencia de x es simplemente {x}, esto es [x]={x}.

Ejemplo 3.4.8
Sea X = {1,2,3,...10}. Defínase xRy si 3 divide a x-y. Puede verificarse que la relación R es
reflexiva, simétrica y transitiva. Esto es, que R es una relación de equivalencia sobre X.
Determinar los elementos de las clases de equivalencia.
Solución
La clase de equivalencia de [1] está formada por todos los x con xR1. Es decir
[1]={x X|3 divide a x-1}={1,4,7,10}.
[2]={2,5,8}.
[3]={3,6,9}.
Estos tres conjuntos forman una partición de X. Obsérvese que
[1]=[4]=[7]=[10].
[2]=[5]=[8].
[3]=[6]=[9].
Esta relación equivalencia quiere decir “se tiene el mismo residuo cuando se divide entre
3”.
Ejemplo 3.4.9
Sea R={(x,y)|x y (mod d), x,y,d Z y d 0}= {(x,y)|x– es divisible por d}, una relación de
equivalencia.
Si R={(x,y)|x y (mod 4) }.
[0]={...,-16,-12,-8,-4,0,4,8,12,16,...}={4n|n Z}.
[1]={...–15,-11,-7,-4,1,5,9,13,17,...}={4n+1|n Z}.
[2]={ ...–14,-10,-6,-2, 2,6,10,14,18,...}={4n+2|n Z}.
[n]={ 4n+n|n Z}.
Teorema 3.4.2
Sea R una relación de equivalencia sobre un conjunto X, para cada a X, sea
[a]={x X|xRa}
Entonces
L(X)={[a]|a X}
Es una partición de X.
De mostración
Hay dos hechos que deben verificarse con el fin de probar que es una partición de X.
i) X= Ai para todo Ai L(X).
ii) L(X) es una familia disjunta por pares.
Sea a X. Puesto que aRa, a [a]. En consecuencia X= Ai lo que verifica i).
Debe demostrarse que L(X) es una familia disjunta por pares. Supóngase que [a] y
[b] L(X) con [a] [b]. Se probará que [a] [b]= . Supóngase por reducción al absurdo, que
para algún x se tienen que x [a] [b]. Entonces xRa y xRb. El resultado anterior muestra que
[x]=[a] y [x]=[b]. Consecuentemente, [a]=[b], lo cual es una contradicción. Por lo tanto,
[a] [b]= y L(X) es una familia disjunta por pares.

3.4.4 El conjunto cociente
Definición 3.4.4 (Conjunto cociente)

La colección de las clases de equivalencia, [x], [y], [z]..., de un conjunto X se denomina
conjunto cociente o conjunto factor de X por R y se escribe simbólicamente como:
X ={[x], [y], [z]...}
R
Teorema 3.4.3
Toda relación de equivalencia R definida sobre un conjunto X, induce en X una partición.
Esta es X , así el conjunto cociente es una partición del conjunto A.
R
Ejemplo 3.4.10
Sea R={(1,1), (1,3), (1,5), (2,2), (2,4), (3,1), (3,3), (3,5), (4,2), (4,4), (5,1), (5,3), (5,5)}
definida sobre X={1,2,3,4,5}.
Las clases de equivalencia son:
[1]={1,3,5}.
[2]={2, 4}.
[3]={1,3,5}.
[4]={2,4}.
[5]={1,3,5}.
Así el conjunto cociente de R es
X [1],[2],[3],[4],[5] [1],[2] 1,3,5 , 2, 4
R
Observe que el conjunto cociente es una partición del conjunto X.
i) [1]={1,3,5} y [2]={2,4} .
ii) [1] [2]= .
iii) [1] [2]={1,3,5,2,4}={1,2,3,4,5}=X.
Con esto verificamos que el conjunto cociente es una partición de X.
Ejemplo 3.4.11
Sea A={-4,-3,-2,-1,0,1,2,3,4,} y R={(x,y)|x(x+1)=y(y+1)}. Determinar si R es una relación
de equivalencia, si la relación es de equivalencia encontrar el conjunto cociente de la relación.
Solución
Reflexiva
R es reflexiva puesto que x(x+1)=x(x+1), por lo que se tiene que (x,x) R.
Simétrica
La relación es simétrica ya que si (x,y) R se tiene que x(x+1)=y(y+1) y como
y(y+1)=x(x+1) se tiene que (y,x) R.
Transitiva
La relación es transitiva, ya que si x(x+1)=y(y+1) y y(y+1)=z(z+1) se tiene que
x(x+1)=z(z+1).
Como la relación es reflexiva, simétrica y transitiva la relación es de equivalencia.
La relación es:

R={(0,0), (0,-1), (1,0), (-1,-1), (1,1), (1,-2), (-2,2), (2,2), (2,-3), (-3,2), (-3,-3), (3,3), (3,-4),
(-4,3), (-4,4), (4,4)}.
Las clases de equivalencia son [0]={0,-1}, [1]={1,-2}, [2]={2,-3}, [3]={3,-4} y [4]={4}.
El conjunto cociente es A R {[ 0], [1], [2], [3], [4]}.
3.5 FUNCIONES
La teoría de funciones es muy amplia, aquí solo nos centraremos en considerar las
funciones como una relación especial.
Definición 3.5.1 (Función)

Una función f de X en Y es una relación de X en Y con las siguientes propiedades:
i) El dominio de f es X.
ii) Si (x,y) f y (x,y’) f entonces y=y’.
La función f de X en Y se denota como f: X→Y
Ejemplo 3.5.1
a) Sean X={3,5}, Y={2,4,6}.
R={(x,y)|x>y} definida en XxY.
R={(3,2), (5,4)}, R es una función por que D R={3,5}=X y los elementos del conjunto X
aparecen sólo una vez. f={(3,2), (5,4}.
b) Sea X={1,2,3}.
R={(x,y)|x=y} definida en XxX.
R={(1,1), (2,2), (3,3)}, R es una función por que D R={1,2,3}=X y los elementos del
conjunto X aparecen sólo una vez. f={(1,1), (2,2), (3,3)}.
c) Sea X={1,2,3}.
R={(1,2), (2,1), (2,3),(3,2)}, R no es una función por que los elementos del conjunto X
aparecen más de una vez.
d) Sea X={1,2,3}.
R={(1,2), (2,1), (2,2),(1,1}, R no es una función por que no aparecen todos los elementos
del conjunto X y además re repiten.
Definición 3.5.2 (Dominio e imagen de una función)

Sea f una función, el conjunto de los primeros elementos posibles en los pares ordenados en
f se denomina dominio de f y se denota por D f ; el conjunto de los segundos elementos posibles
en los pares ordenados se denomina imagen de f y se denota por If., es decir:
Df={x|(x,y) f}
If={y|(x,y) f}

Ejemplo 3.5.2
Considere las funciones de los incisos a) y b) del ejemplo 3.5.1
a) Sean X={3,5}, Y={2,4,6} y f={(3,2), (5,4}.
El dominio de f es Df = {3,5}, la imagen de f es I f = {2,4}.
b) Sea X={1,2,3} y f={(1,1), (2,2), (3,3)}.

El dominio de f es Df = {1,2,3}, la imagen de f es I f = {1,2,3}.
Definición 3.5.3 (Función uno a uno)

Una función f:X→Y es uno a uno si para cada y Y existe a lo más una x X tal que
(x,y) f. De manera equivalente si (x,y) f y (z,y) f entonces x=y.
Ejemplo 3.5.3
a) Sean X={3,5}, Y={2,4,6} y f={(3,2), (5,4}, f es uno a uno.
b) Sean X={1,2,3} y f={(1,1), (2,2), (3,3)}, f es uno a uno
c) f={(1,b), (3,a), (2,c)}, X={1,2,3} y Y={a,b,c,d}, f es uno a uno.
d) Sea X={1,2,3} y f={(1,1),(2,1)(3,1)} definida en XxX, f no es uno a uno por que para y=1
hay más de una X. En particular esta función se llama función constante.
Nota: Observe que para que una relación sea función no se debe repetir la primera coordenada y
para que sea uno a uno no se repite la segunda coordenada, luego para tener una función uno a
uno no se debe de repetir ni la primera ni la segunda coordenada.
Definición3.5.4 (Función sobre)

Si f es una función de X en Y, se dice que f es sobre Y siempre y cuando para toda y Y
exista una x X tal que (x,y) f. En otras palabras la imagen de f es Y.
Ejemplo 3.5.4
a) Sean X={3,5}, Y={2,4,6} y f={(3,2), (5,4}, f no es sobre por que If={2,4} Y.
b) Sean X={1,2,3} y f={(1,1), (2,2), (3,3)}, f es sobre.
c) Sean X={1,2,3}, Y={a,b,c} y f={(1,a), (2,c), (3,b)}, f es sobre.
Definición 3.5.5 (Función biyectiva)

Una función f de X en Y es biyectiva si es uno a uno y sobre.
Ejemplo 3.5.5
a) La función definida en el inciso b) del ejemplo 3.5.1 es biyectiva.
b) Sean X={1,2,3}, Y={a,b,c} y f={(1,a), (2,c), (3,b)}, f es una función biyectiva.
Definición 3.5.6 (Función inversa)

Supongamos que f es una función uno a uno y sobre de X en Y. La relación inversa de f se
denota por f-1 y se define como: f-1(x)={(y,x)│(x,y) f} definida en YxX.
Ejemplo 3.5.6

Sean X={1,2,3}, Y={a,b,c} y f={(1,a), (2,c), (3,b)}.

Como f es uno a uno y sobre es biyectiva y por lo tanto tiene inversa, su inversa es:
f –1={(a,1), (2,c),(3.b)}.
Ejercicios: unidad III
3.1 Expresar las siguientes relaciones definidas en X={1,2,3,4}.

a) R1={(x,y) | x=y}.
b) R2={(x,y) | 3x=y}.
c) R3={(x,y) | x=y}.
d) R4={(x,y) | 2x =y+1}.
e) R5={(x,y) | x y}.
f) R6={(x,y) | x es múltiplo de y}.
g) R7={(x,y) | y es múltiplo de x}.
h) R8={(x,y) | (x-y) es un múltiplo no nulo de 2}.
i) R9={(x,y) | x es divisible por y}.
j) R10={(x,y) | x2 y}.
3.2 Expresar la relación R={(x,y) | x Z, y N, x2+y2<10}.
3.3 Trazar el digrafo de las siguientes relaciones.

a) R={(1,2), (2,1), (3,3), (1,1), (2,2)} sobre X={1,2,3}.
b) R={(1,2), (2,3), (3,4), (4,1)} sobre X={1,2,3,4}.
c) R={(x,y)|x=y} sobre X={1,2,3,4}.
d) R={(x,y)|3x=y} sobre X={1,2,3,4}.
e) R={(x,y)|x=5y} sobre X={1,2,3,4}.
f) R={(x,y)|2x=y+1} sobre X={1,2,3,4}.
g) R={(x,y)|x y} sobre X={1,2,3,4}.
h) R={(x,y)|x2 y} sobre X={1,2,3,4}.
3.4 Sea R sobre {1,2,3,4,5} definida por R={(x,y) | 3 divide a x-y}.

a) Enumere los elementos de R.
b) Determine el dominio de R.
c) Determine la imagen de R.
3.5 Sea R sobre {1,2,3,4,5} definida por R={(x,y) | x+y≤6}

a) Enumere los elementos de R
b) Determine el dominio de R
c) Determine la imagen de R
3.6 Sea R sobre {1,2,3,4,5} definida por R={(x,y) | x=y–1}.

a) Enumere los elementos de R.
b) Determine el dominio de R.
c) Determine la imagen de R.

3.7 Determina si cada una de las relaciones es reflexiva, irreflexiva, simétrica, antisimétrica y
transitiva.
a) R={(x,y) | x=y} sobre X={1,2,3,4}.
b) R={(x,y) | 3x =y} sobre X={1,2,3,4}.
c) R={(x,y) | x =5y} sobre X={1,2,3,4}.

d) R={(x,y) | 2x =y+1} sobre X={1,2,3,4}.
e) R={(x,y) | x y} sobre X={1,2,3,4}.
f) R={(x,y) | x2 y} sobre X={1,2,3,4}.
g) R={(x,y) | 3 divide a x-y} X={1,2,3,4,5}.
h) R={(x,y) | x+y≤6} X={1,2,3,4,5}.
i) R={(x,y) | x=y–1} X={1,2,3,4,5}.
3.8 Determinar si cada relación definida sobre el conjunto de los enteros positivos es reflexiva,
irreflexiva, simétrica, antisimétrica o transitiva.
a) (x,y) R si x=y2.
b) (x,y) R si x>y.
c) (x,y) R si x y.
d) (x,y) R si el m.c.d. de x y y es 1.
e) (x,y) R si 3 divide a x–y.
3.9 Dado S={1,2,3,4} y una relación R sobre S, definida por:

R={(1,2),(4,3),(2,2),(2,1),(3,1)}Demuestre que R no es transitiva. Encuentre una relación
R1 R de modo que R1 sea transitiva ¿Puede encontrar otra relación R2 R que sea también
transitiva?.
3.10 Sea X un conjunto no vacío. Se define una relación sobre P(X), el conjunto potencia de X
como (A,B) R si A B. ¿Es esta una relación reflexiva, irreflexiva, simétrica, antisimétrica
o transitiva?.
3.11 Sea A y P(A) el conjunto potencia de A, la relación definida por P(x,y): x y= , ¿qué
propiedades cumple?.
3.12 Dar ejemplos de relaciones sobre X={1,2,3,4} que posea las propiedades indicadas.
a) Reflexiva, simétrica, no transitiva .
b) Reflexiva, no simétrica, no transitiva.
c) Reflexiva, antisimétrica, no transitiva.
d) No reflexiva, simétrica, no antisimétrica, transitiva.
e) No reflexiva, no simétrica, transitiva.
f) No reflexiva, simétrica, transitiva.
g) Simétrica, antisimétrica.
3.13 Sean R y S relaciones sobre X. Determine si cada una de las proposiciones es verdadera o
falsa. Si es falsa, de un ejemplo.
a) Si R y S son transitivas, entonces R S es transitiva.

b) Si R y S son transitivas, entonces R  S es transitiva.

c) Si R y S son reflexivas, entonces R S es reflexiva.
d) Si R y S son reflexivas, entonces R S es reflexiva.
e) Si R y S son reflexivas, entonces R  S es reflexiva.
f) Si R y S son simétricas, entonces R S es simétrica.

g) Si R y S son simétricas, entonces R  S es simétrica.
h) Si R y S son antisimétricas, entonces R S es antisimétrica.
i) Si R y S son antisimétricas, entonces R S es antisimétrica.
j) Si R y S son antisimétricas, entonces R  S es antisimétrica.
3.14 ¿Cuál es el error en el siguiente razonamiento que pretende demostrar que si una relación
en X es simétrica y transitiva, entonces también es reflexiva?
Sea x X. Usando simetría tenemos que (x,y) y (y,x) están en R. Como (x,y), (y,x) por la
propiedad transitiva (x,x) R. Por consiguiente R es reflexiva.
3.15 Determine si las siguientes relaciones son transitivas.

a) R1={(1,1)}.
b) R2={(1,2),(2,2)}.
c) R3={(1,2),(2,3),(1,3),(2,1)}.
3.16 Sean R={(1,2), (1,3), (2,2), (2,1), (4,4)} y S={(1,1), (1,3 ), (2,3), (3,1)}
Calcular
a) R°S.
b) S°R.
c) R°(S°R).
d) (R°S)°R.
e) R°R.
f) S°S.
g) R°R°R

Unidad V. Teoría de Grafos Caminos y circuitos
3.17 Determinar las propiedades que satisfacen las relaciones siguientes, definidas sobre el
conjunto de los enteros positivos; así como el tipo de relación.
a) R={(x,y) | x divide a y (x|y)}.
b) R={(x,y) | x+y es par}.
c) R={(x,y) | x–y es par}.
d) R={(x,y) | x3+y2 es par}.
e) R={(x,y) | x+y es múltiplo de 2}.
f) R={(x,y) | x=y}.
g) R={(x,y) | 7 divide a x–y (7|x–y)}.
h) R={(x,y) | x2 y2}.
i) R={(x,y) | x>y}.
j) R={(x,y) | x y 3 }.
k) R={(x,y) | x–y es múltiplo de 2}.
l) R={(x,y) | 2 divide a–y}.
m) R={(x,y) | 5 divide a x–y}.
n) R={(x,y) | x+y es impar}.
o) R={(x,y) | 3 divide a x2–y2}.
3.18 Determine si la relación dada es una relación de equivalencia sobre {1,2,3,4,5}. Si la

relación es de equivalencia, dar las clases de equivalencia, el conjunto cociente y mostrar
que es una partición.
a) {(1,1), (2,2), (3,3), (4,4), (5,5), (1,3), (3,1)}.
b) {(1,1),(2,2),(3,3),(4,4),(1,3), (3,1), (3,4), (4,3)}.
c) {(1,1), (2,2), (3,3), (4,4)}.
d) {(1,1), (2,2), (3,3), (4,4), (5,5), (1,5), (5,1), (3,5), (5,3), (1,3), (3,1)}.
e) {(x,y)│1≤x≤5, 1≤y≤5}.
f) {(x,y)│4 divide a x–y}.
g) {(x,y)│3 divide a x+y}.
h) {(x,y)│x divide a 2–y}.
3.19 Sea P una partición del conjunto X={1,2,3,4}. Defínase xRy si x y y pertenecen al mismo
conjunto de la partición. Dar la relación de equivalencia y las clases de equivalencia de X
inducidas por R.
a) {{1,2}, {3,4}.
b) {{1}, {2}, {3,4}}.
c) {{1}, {2}, {3}, {4}}.
d) {{1,2,3}, {4}}.
e) {{1,2,3, 4}}.
f) {{1}, {2,4}, {3}}.
3.20 Sea X={Montemorelos, Monterrey, Veracruz, Xalapa, Orizaba, Córdoba, Guadalajara}

a) Definir una relación R sobre X, como xRy si x y y están en el mismo estado.
b) Demostrar que R es una relación de equivalencia.

c) Expresar las clases de equivalencia de X inducidas por R.
3.21 Proporcionar un ejemplo, mediante una lista de pares ordenados, de una relación de
equivalencia sobre {1,2,3,4,5,6,7} que tenga exactamente 4 clases de equivalencia.
3.22 Sea X={1,2,3,4,5,6,7,8,9,10}. Se define una relación R sobre X X por (a,b)R(c,d) si

a+d=b+c.
a) Demostrar que R es una relación de equivalencia sobre X X.
b) Escribir un elemento de cada una de las clases de equivalencia de X X.
3.23 Sea X = {1,2,3,4,5,6,7,8,9,10} se define una relación R sobre X X por (a,b)R(c,d) si

ad=bc.
a) Pruebe que R es una relación de equivalencia sobre X X.
b) Enuncie un elemento de cada una de las clases de equivalencia de X X.
3.24 Sean R1 y R2 dos relaciones de equivalencia sobre X.

a) Probar que R1 R2 es una relación de equivalencia sobre X .
b) Señalar las clases de equivalencia de R1 R2 en términos de las clases de equivalencia de
R1 y las clases de equivalencia de R 2.
3.25 Sea Z el conjunto de los números enteros. Determinar si la relación definida sobre Z es una
relación de equivalencia.
a) R={(a,b)│a Z, b Z y a+b es múltiplo de 2}.
a
b) R={(a,b)│a Z, b Z y Z }.
b
c) R={(a,b)│a Z, b Z y a=3b}.
23. ¿Cuántas relaciones de equivalencia hay en el conjunto {1,2,3}?
24. Sea R una relación reflexiva y transitiva sobre X. Demuestre que R R-1 es una
relación de equivalencia sobre X.
3.26 Determine si cada relación es una función de X={1,2,3,4} en Y={a,b,c,d}. Si es una

función, determine su dominio y rango y determine si es uno a uno o sobre. Si es uno a uno
o sobre, proporcione una descripción de la función inversa como un conjunto de pares
ordenados y proporcione el dominio y rango de la función inversa.
¿Deben aparecer todos los elementos?
a) {(1,a), (2,a), (3,c), (4,b)}.
b) {(1,c), (2,a), (3,b), (4,c), (2,d)}.
c) {(1,c), (2,d), (3,a), (4,b)}.
d) {(1,d), (2,d), (4,a)}.
e) {(1,b), (2,b), (3,b), (4,b)}.
3.27 Sea f={(x,x2)│x X} una función de X={-5,-4,... ,4,5} al conjunto de enteros, escriba f
como un conjunto de pares ordenados. ¿Es uno a uno o sobre?.

3.28 Determine si cada una de las siguientes relaciones es una función. Si una relación es una
función, determine su imagen.
a) {(x,y)│x, y Z, y =x2+7}, una relación de Z en Z.
b) {(x,y)│x, y R, y2=x}, una relación de R en R.
c) {(x,y)│x, y R, y=3x+1}, una relación de R en R.
d) {(x,y)│x, y R, x2+y2=1} , una relación de R en R.
3.29 Determine si las siguientes funciones son uno a uno y determine también su imagen.
a) f: Z→Z, f(x)=2x+1.
b) f: Q→Q, f(x)=2x+1.
c) f: Z→Z, f(x)=x3 -x.
d) f: R→R, f(x)=ex.
e) f: , →R, f(x)=senx.
2 2
f) f: [0, ]→R, f(x)=sen x.
Unidad IV. Los Números Reales
4.1 El principio de inducción matemática.
4.2 Los números enteros

4.2.1 Descripción y operaciones.
4.2.2 Propiedades.
4.2.3 La congruencia módulo n.
4.2.4 Expansión en base b de un número entero.
4.3 Los números racionales

4.3.1 Descripción y operaciones
4.3.2 Propiedades
4.4 Los números reales

4.4.2 Propiedades
4.4.3 Expansión en base b de un número real.
4.1 EL PRINCIPIO DE INDUCCIÓN MATEMÁTICA
En el lenguaje cotidiano, la palabra inducción indica sacar conclusiones generales

examinando algunos casos particulares.
Principio de inducción matemática: supóngase que se tiene una proposición S(n) para cada
entero positivo n, la cual es verdadera o falsa, consideremos que:

a) S(1) es verdadera
b) S(i) es verdadera para todo i<n+1, entonces S(n+1) es verdadera.
De modo que S(n) es verdadera para todo entero positivo.
A la consideración a) se le llama paso básico y a la consideración b) se le llama paso

inductivo.
Para verificar el paso inductivo se supondrá que S(i) es verdadera para toda i<n+1 y se
probará que S(n+1) es verdadera.
Esta manera de formular la inducción matemática recibe el nombre de forma fuerte de

inducción matemática.
De esta manera para resolver problemas usando inducción matemática se realizan los
siguientes pasos.
a) Se prueba que S(1) es verdadera.
b) Se supone que S(n) es verdadera.
c) Se demuestra que S(n+1) es verdadera.
El principio de inducción matemática se usa para probar que un grupo de enunciados se

pueden poner en correspondencia uno a uno con el conjunto de los números naturales.
En la formulación del principio de inducción se empezó con el elemento 1, sin embargo,

esto no es necesario, ya que es posible empezar con cualquier número natural n 0, incluso es
posible iniciar con 0 o con un número negativo. En este caso la condición es cierta para toda
n n 0.
Ejemplo 4.1.1
Demuestre que:
n(n 1)
1+2+…+n= para toda n 1
2
Lo anterior también podría expresarse como:
n
n(n 1)
i .
i 1 2
Demostración
b) Paso básico: se demuestra que S(1) es verdadera, esto es, la expresión se cumple para n=1.
1(1 1) 2
1= 1
2 2
c) Paso inductivo: supóngase que S(n) es verdadero.
n(n 1)
1+2+…+n=
2
d) Demuéstrese que S(n+1) es verdadera, esto es, se quiere demostrar que
(n 1)[( n 1) 1] (n 1)( n 2)
S(n+1)=1+2+…n+(n+1)=
2 2
Para demostrar que S(n+1) se cumple se usa el paso inductivo de la siguiente manera:

La expresión 1+2+…n+(n+1) se divide en dos partes: Primera parte 1+2+…n, segunda

parte n+1.
se sustituye
n(n 1) n(n 1)
1+2+…n por , es decir, S(n+1)=1+ 2+…n+(n+1) = (n 1) .
2 2
n(n 1)
Posteriormente se manipula la expresión (n 1) de la siguiente forma:
2
n(n 1) n(n 1) 2(n 1) (n 1)( n 2) (n 1)[( n 1) 1]
(n 1) = = = .
2 2 2 2
Con esto queda demostrado que S(n+1) es verdadera, Por lo tanto se concluye que la
propiedad es válida para todos los enteros positivos.

Ejemplo 4.1.2
Demostrar que
n
5n(n 1)
5i es válida para todos los enteros positivos.
i 1 2
Expandiendo la expresión se tiene
5n(n 1)
5+10+15+20+…+5n= .
2
Demostración
a) Paso básico: para n=1, se tiene que:
5(1) (1) 1 10
S(1)=5= 5 se cumple.
2 2
b) Paso inductivo: se supone que la expresión se S(n) se cumple.
5n(n 1)
5+10+15+20+...+5n=
2
c) Demuéstrese que S(n+1) es verdadera, esto es, se quiere demostrar que
5(n 1)(( n 1) 1) 5(n 1)(n 2)
5 10 15 20 ... 5k 5(n 1)
2 2
5n(n 1) 5n(n 1) 10(n 1)
5
10
15
20
...
5n 5(n 1) +5(n+1)= =
2 2
5 n(n 1) 2(n 1) 5(n 1)(n 2)
.
2 2
Luego la propiedad es válida para todos los en teros positivos.
Ejemplo 4.1.3
n
Demostrar que la propiedad 2i 2n 1
2 es válida para todos los enteros positivos
i 1
2+22+23+...+2n=2n+1–2.
Demostración
c) Verificar que S(1) es verdadera.
S(1)=2=21+1–2=4–2=2.
d) Hipótesis de inducción: Suponga que se cumple S(n).
2+22+23+...+2n=2n+1–2.
e) Demostrar que se cumple S(n+1).
2 22 23 ... 2 n 2n 1
2 (n 1) 1
2 2n 2
2
2 3 n
22 2...
2 2n 1= 2n 1
2 +2n+1=22n+1–2=2(n+1)+1–2=2(n+2)–2.
Así, la propiedad es válida para todos los enteros positivos.

Ejemplo 4.1.4
n
1 n
Mostrar que la propiedad se cumple para todos los enteros positivos.
i 1 i (i 1) n 1
n
1 1 1 1 1 n
...
i 1
i (i 1) (1)( 2) (2)(3) (3)( 4) n(n 1) n 1
Demostración:
a) Paso básico: para n=1, se tiene que:
1 1 1 1
S(1)=
2 (1)( 2) 1 1 2
b) Hipótesis de inducción; suponemos que S(n) se cumple.
1 1 1 1 n
...
(1)( 2) (2)(3) (3)( 4) n(n 1) n 1
c) Demostrar que se cumple S(n+1).
1 1 1 1 1 n 1 n 1
...
(1)( 2) (2)(3) (3)( 4) n(n 1) (n 1)(( n 1) 1) (n 1) 1 n 2
1 1 1 1 1 n 1
...
(1)( 2) (2)(3) (3)( 49 n(n 1) (n 1)(( n 1) 1) n 1 (n 1)( n 2)
  
n(n 2) 1 n 2 2n 1 (n 1) 2 n 1
(n 1)( n 2) (n 1)( n 2) (n 1)( n 2) n 2
Así, la propiedad es válida.
Ejemplo 4.1.5
Mostrar que la propiedad n<2 n para n=0,1,2,…es válida.
Demostración
a) Paso básico: se demuestra que S(0) es verdadera, esto es, la expresión se cumple para n=0.
S(0)=0<2 0 1 y 0 si es menor que 1.
b) Paso inductivo: supóngase que S(n) es verdadero.
n<2n.
c) Demuéstrese que S(n+1) se cumple, esto es, se quiere demostrar que
(n+1)<2n+1
Por b) sabemos que n<2n se cumple, sumando 1 en ambos lados de la desigualdad se tiene:
n+1<2n+1<2n+2 4.1.1
n n+1
Ahora bien el problema se reduce a demostrar que 2 +2<2 , para n>1.
Se aplica el proceso de inducción nuevamente.
b) Paso básico verificar que S(2) se cumple
S(2)=22+2=6<22+1=8.
c) Paso inductivo, Supóngase que S(n) se cumple

2n+2<2n+1.

d) Demuéstrese que S(n+1) se cumple.

2n+1+2<2(n+1)+1 o bien 2n+1+2<2n+2
Sabemos por b) que 2 n+2<2n+1, multiplicando ambos lados de la desigualdad por 2 se

tiene 2(2n+2)<2(2n+1) o bien
22n+4<2(n+1)+1, es decir 2n+1+4<2n+2, 2n+1+2<2n+2 -2<2n+2.
Por lo tanto 2n+2<2n+1 se cumple para n>1.
Usando el resultado anterior en la ecuación 4.1.1 se tiene

n+1<2n+1<2n +2<2n+1.
Luego n+1<2n+1, como se quería mostrar.
Por lo tanto n<2n para toda n=0,1,2,3,…
Ejemplo 4.1.6
Mostrar que 5n–1 es divisible entre 4 para n=1,2,…
Demostración
a) Paso básico verificar que S(1) se cumple
S(1)=5 1 1 4 y 4 si es divisible entre 4
b) Paso inductivo, Supóngase que S(n) se cumple
S(n)=5n–1 es divisible entre 4
c) Demuéstrese que S(n+1) se cumple.
Por demostrar que 5n+1–1 es divisible entre 4.
Por el paso inductivo sabemos que
5n-1 es divisible entre 4, esto significa que, al dividir 5 n -1 entre 4 el resultado es un número
entero, esto es,
5n 1
R(entero) , en consecuencia 5n–1=4R.
4
Multiplicando por 5 ambos lados se tiene
5(5n–1)=5(4R).
5n+1–5=5(4R).
5n+1–1–4=5(4R).
5n+1–1=5(4R)+4=4(5R+1).
Como R es un entero, se tiene que R1=(5R+1) es un entero por lo que 4R1 es un número
divisible entre 4, por lo tanto 5 n+1–1 es divisible por 4.
Así, la propiedad es válida para todo n 1.
4.3 LOS NÚMEROS ENTEROS
4.2.5 Descripción y operaciones.
Definición 4.2.1 (Número entero)

Número entero es cualquier elemento del conjunto formado por los números naturales, sus
opuestos y por el cero. Son una extensión de los números naturales y surgen de la necesidad de
solucionar problemas como: resolver la operación 6-8, en el conjunto de los números naturales no

tiene solución, ya que no existe ningún número que sumado a 8 dé por resultado 6. Esta
diferencia si tiene solución en los enteros, el número negativo –2.
En la matemática moderna el conjunto de los números enteros, que se designan con la letra
Z, llegan hasta el infinito hacia ambos lados de una recta numérica, por tanto, en rigor no existe
un comienzo, salvo que como tal se considere el CERO. Los números negativos permiten contar
nuevos tipos de cantidades (como los saldos deudores) y ordenar por encima o por debajo de un
cierto elemento de referencia (las temperaturas superiores o inferiores a 0 grados, los pisos de un
edificio por encima o por debajo de la entrada al mismo, etc.).
4.2.6 Propiedades.
En los enteros se definen dos operaciones: la adición y la multiplicación, las cuales

cumplen los axiomas y propiedades siguientes.
Axioma 1.2.1. La suma de números enteros es conmutativa, es decir, si a,b Z entonces

a+b=b+a.
Axioma 1.2.2. La suma de enteros es asociativa, es decir, si a,b,c Z entonces

(a+b)+c=a+(b+c).
Axioma 1.2.3. Existe en Z un elemento neutro para la suma, el 0. Es decir, si a Z,

a+0=0+a=a.
Axioma 1.2.4. Para cada a en Z existe en Z su inverso aditivo que se denota por –a, esto es,
a+(–a)=(–a)+a=0.
Axioma 1.2.5. El producto de números enteros es conmutativo, es decir, si a, b Z entonces

ab=ba.
Axioma 1.2.6. El producto en Z es asociativo, es decir, si a,b,c Z entonces (ab)c=a(bc).
Axioma 1.2.7. Existe en Z un elemento neutro para la multiplicación, el 1. Es decir, si a Z

a(1)=(1)a=a.
Axioma 4.2.8. En Z el producto distribuye a la suma, es decir, si a,b,c Z entonces

a(b+c)=ab+ac
(a+b)c=ac+bc.
Propiedad 4.2.1: (Ley de cancelación) Si a,b y c son enteros y a+b=a+c, entonces b=c.
Propiedad 4.2.2: (Ley de cancelación por la derecha) Si a, b y c son enteros y a+c=b+c,

entonces a=b.
Propiedad 4.2.3: Para todo entero a, se tiene 0a=0.

Propiedad 4.2.4. Si a, b son enteros, entonces

(–a)b=–(ab).
(–a)(–b)=ab.
Definición 4.2.2 (diferencia de dos enteros)

Si a,b Z la diferencia a–b se define en términos de la suma de la siguiente forma:
a–b=a+(–b).
Proposición 4.2.1
Si a,b,c Z, entonces a(b–c)=ab–ac.
4.2.7 La congruencia módulo n.
a
Si a y b son números enteros con b 0, al formar el cociente este puede o no ser un
b
número entero; cuando el cociente es un número entero decimos que b divide a a. Este concepto
es la base para la divisibilidad.
Definición 4.2.3(divisibilidad)
Si a y b son números enteros, decimos que b divide a a, si existe un entero q tal que,
a=bq. Si restringimos el valor de b a b 0, la definición es equivalente a considerar que el cociente
a
q . Para simbolizar que b divide a a utilizamos la notación b|a, el símbolo b | a indica que b
b
no divide a a.
Propiedad 4.2.5 (Propiedad reflexiva): Para todo número entero a, se tiene que a divide a a.
Propiedad 4.2.6 (Propiedad transitiva): Si a, b y c son números enteros tales que a divide a b y
b divide a c, entonces a divide a c. Simbólicamente Si a|b y b|c entonces a|c.
Corolario 4.2.1: Si a y b son enteros, las condiciones siguientes son equivalentes:
(i) a divide a b (a|b)
(ii) |a| divide a |b| (|a|||b|)
Proposición 4.2.2 (Propiedad de simetría): Si a y b son dos enteros distintos de cero tales que
a|b yb|a entonces a=b.
Proposición 4.2.3:Si a|b y a|c entonces a|(b+c)
Proposición 4.2.4: Si a|b y c es un entero arbitrario, entonces a|bc.
Corolario 4.2.2: Si a, b y c son enteros tales que c|a y c|b, entonces c|(ar+bs)
Definición 4.2.4 (Combinación lineal)

Si a, b, r y s son enteros, a la expresión ar+bs se le denomina combinación lineal de a y b.
Corolario 4.2.3: Un entero c divide a los enteros a y b si y sólo si c divide a cualquier

combinación lineal de a y b.
Definición 4.2.5 (Máximo común divisor)

Sean a y b enteros, el conjunto de los divisores comunes de a y b, es igual a la intersección

del conjunto de los divisores de a y el conjunto de los divisores de b. Así, el máximo común
divisor de a y b, denotado por mcd(a,b) es el mayor de los elementos del conjunto de los
divisores comunes de a y b.
Ejemplo 4.2.1
Determinar mcd(18,24)
Los divisores de 18 son 1, 2, 3, 6, 9
Los divisores de 24 son 1, 2, 3, 4, 6, 8, 12, 24
Divisores comunes de 18 y 24 son
{ 1, 2, 3, 6, 9} { 1, 2, 3, 4, 6, 8, 12, 24}={ 1, 2, 3, 6}
Así, mcd(18,24)=6.
Para determinar el máximo común divisor de dos números enteros a y b, es posible

considerar sólo los divisores positivos, ya que mcd(a,b)=mcd(|a|,|b|).
Definición 4.2.6 (Primos relativos)

Se dice que dos enteros a y b son primos entre sí (o primos relativos) si su máximo común
divisor es 1.
Ejemplo 4.2.2
Determinar si los números12 y 25 son primos relativos.
Los divisores de 12 son: 1, 2, 3, 4, 6 y 12.
Los divisores de 25 son: 1, 5 y 25.
Luego mcd(12, 25) = 1, por consiguiente 12 y 25 son primos relativos.
Definición 4.2.7 (Mínimo común múltiplo)

Sean a y b dos enteros distintos de cero. El conjunto de los múltiplos comunes de a y b, es
igual a la intersección del conjunto de los múltiplos de a y el conjunto de los múltiplos de b. El
conjunto de múltiplos comunes positivos de a y b tiene al menos un elemento, este es ab. Y por
el axioma del buen orden este tiene un elemento mínimo, el cual se denomina mínimo común
múltiplo de a y b, que se denota por mcm(a,b).
Ejemplo 4.2.3
Determinar el mcm(6, 10).
Los múltiplos positivos de 6 son: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, …
Los múltiplos positivos de 10 son: 10, 20, 30, 40, 50, 60, 70,…
Así el conjunto de múltiplos comunes de 6 y 10 es {30, 60, 90,…}.
El mcm(6,10)=30.
Definición 4.2.8 (congruencia)

Se dice que dos enteros a y b son congruentes, módulo m, si m divide a la diferencia a–b,
simbólicamente
a b (mod m) si y solo si m| (a–b)
a b
Recordemos que m|(a–b) significa que existe un k Z tal que k o bien a=b+km.
m

Ejemplo 4.2.4
17 2 (mod 5) por que 5 divide a 17-2=15.
–7 –49 (mod 6) por que 6 divide a -7–(-49)=-7+49=42.
Teorema 4.2.1: La congruencia módulo m es compatible con la suma de los números enteros,
esto es:
a b (mod m) y c d (mod m) entonces (a+c) (b+d) (mod m).
Demostración
Hipótesis a b (mod m)
c d (mod m)
Conclusión a+c b+d (mod m)
Como a b (mod m) entonces m|(a–b) y como c d (mod m) entonces m|(c–d)

Por las propiedades de divisibilidad se tiene
m|[(a–b)+(c–d)]
m|(a–b+c–d)
m|[(a+c)–(b+d)]
a+c b+d (mod m). Así, el teorema es válido.
Proposición 4.2.5: Para a, b, c en Z se tiene que

i) a b (mod m) entonces a+c b+c (mod m)
ii) a b (mod m) entonces ac bc (mod m)
Demostración
i) Hipótesis a b (mod m)
Conclusión a+c b+c (mod m)
Por hipótesis a b (mod m) entonces m|(a–b)

Por otro lado, a–b=a+c–c–b=(a+c)–(b+c).
Luego, m|[(a+c)–(b+c)]
Por lo tanto a+c b+c (mod m)
Así, i) es válido.
Una demostración semejante se realiza para demostrar ii).
Propiedad 4.2.7: Si a=mq1+r1 0 r1 m con a y b enteros

b=mq2+r2 0 r2 m
a b (mod m) si y sólo si r1=r2.
Esta propiedad nos dice que son congruentes todos aquellos números enteros que tengan el
mismo residuo.
El entero m, determina el conjunto, que denotamos con Z m, de las clases residuales módulo
m, esto es, en el conjunto se encuentran todos aquellos elementos que son los residuos obtenidos

de dividir cualquier entero entre m. Por ejemplo si m=6, Zm={0,1,2,3,4,5} porque al dividir
cualquier entero entre 6 encontramos como residuos a 0, 1, 2, 3, 4, ó 5.
4.4.4 Expansión en base B de un número entero
Existen varios sistemas de numeración, cada uno de ellos determina una base para la
representación de cualquier número entero, inclusive de un número real. Consideremos, entonces,
algunos sistemas de numeración.
Sistema de numeración decimal

El sistema de numeración decimal es aquel en el que se combinan de una manera
sistemática diez símbolos: 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9 para representar las cantidades y ejecutar con
ellos las operaciones de la aritmética.
En este sistema un número entero se representa como S5 S4 S3 S2 S1 S0. en el que Si es uno

de los símbolos que usamos en este sistema de numeración, también es posible representar el
número en términos de la base, en este caso en términos de la base 10.
Ejemplo 4.2.5
El número 4 679 321 es un número entero.
Considerando la notación de un número entero se tiene que S 0=1, S1=2, S2 =3, S3=9, S4=7,
S5=6 y S6=4.
Este número puede representarse como una suma, de la siguiente forma:

4 679 321=4 000 000+600 000+70 000+9 000+300+20+1
=4 1 000 000+6 100 000+7 10 000+9 1000+3 100+2 10+1 1
=4 106+6 105+7 104+9 103+3 102+2 101+1 100
Esta última es la representación del número entero en base 10.
La representación de un número entero en base 10 es:

N10=...+S4 104+S3 103+S2 102+S1 101+S0 100.
Donde cada Si es un símbolo cualquiera de los 10 que se consideran en este sistema y

donde el subíndice de S coincide con el exponente del 10. Esta representación se denomina
expansión en base 10 de un número entero.
Otros sistemas de numeración

Otros sistemas de numeración son: binario, ternario, cuaternario, etc. Estos se presentan a
continuación, indicando su base, su nombre y sus símbolos.
BASE NOMBRE SIMBOLOS DE LA BASE

2 Binario 0, 1
3 Ternario 0, 1, 2
4 Cuaternario 0, 1, 2, 3
5 Quinario 0, 1, 2, 3, 4

6 Hexal 0, 1, 2, 3, 4, 5
7 Septal 0, 1, 2, 3, 4, 5, 6
8 Octal 0, 1, 2, 3, 4, 5, 6, 7
9 Nonario 0, 1, 2, 3, 4, 5, 6, 7, 8
10 Decimal 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
11 Undecimal 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A
12 Duodecimal 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B
13 Tridecimal 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C
14 Tetradecimal 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D
15 Pentadecimal 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E
16 Hexadecimal 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
De estos sistemas, los más usados son: binario, octal, decimal y hexadecimal.
La forma general, para representar un número entero en cualquier base, es:
NB=…+S4 B4+S3 B3+S2 B2+S1 B1+S0 B0
Donde B es la base del sistema y los Si son símbolos del sistema considerado.
Esta representación de cualquier número entero, se denomina expansión en base B de un
número entero.
Conversión del sistema decimal a otro sistema numérico

El proceso de conversión de un número en sistema decimal a otro sistema de numeración,
se basa en la realización de divisiones sucesivas. Iniciamos dividiendo el número entero entre la
base, el residuo es S0; luego, el cociente se divide entre la base, el residuo es S 1; así continuamos
hasta obtener un cociente menor que la base, este cociente es el último Si. El número en base b se
forma con los residuos y el último cociente, es decir, …S 4S3 S2 S1S0 .
Ejemplo 4.2.6
Representar el número 45 en base 4.
11 2
4 45 4 11 (S2) 4510=2314
1 3
S0 S1
Expresaremos la operación de división de dos números a y b como:

a=b (q)+r donde q representa al cociente y r al residuo.
Usando esta notación en el ejemplo anterior se tiene:

45=4(11)+1 S0=1
11=4(2)+3 S1=3 y como r=3<4, entonces S2=2.
El número en base cuatro es S2S1 S0=231.
Ejemplo 4.2.7
Representar el número 37 en base 2.

37=2(18)+1 S0=1.
18=2(9)+0 S1=0.
9=2(4)+1 S2=1.
4=2(2)+0 S3=0.
2=2(1)+0 S4=0 y S5=1.
Así, el 37 se representa por S5S4 S3 S2S1 S0, luego 3710=1001012.
Conversión de otro sistema numérico al sistema decimal

Para realizar la conversión de un número en cualquier base (diferente de 10), a la base 10,
se representa el número con la expansión en la base B y se simplifica usando la aritmética
decimal.
Ejemplo 4.2.8
Convertir el número 4534231 6 a base decimal.
Expresamos el número 4534231 6 en expansión de la base 6.
4 534 2316=4 66+5 65+3 64+4 63+2 62+3 61+1 60
=4 46 656+5 7 776+3 1296+4 216+2 36+3 6+1 1
=186 624+38880+3888+ 432+72+18+1
=229 915.
4.5 LOS NUMEROS RACIONALES
Los números racionales se denominan también números fraccionarios, y están formados

por el cociente de números enteros. Surgen ante la necesidad de solucionar problemas como:
resolver operaciones, como la división de 9 entre 5, la cual no tiene solución en Z, porque no
existe un número entero que multiplicado por 5 sea igual a 9. Esta operación tiene solución en los
9
racionales donde existe el número racional , que al multiplicar por 5 es igual a 9. El conjunto
5
de los números racionales se designan con la letra Q.
Llamamos fracción a todo par de números enteros, dados en un cierto orden, de tal modo
que el primero no sea múltiplo del segundo y éste sea distinto de cero; esto es:
a
(a,b) Z (Z–{0}) a Z y b (Z–{0})
b
Decimos que b pertenece al conjunto de los enteros, excluido el cero, porque el divisor
nunca puede tomar el valor de cero. El número a se denomina numerador de la fracción y al
número b el denominador, ambos se llaman términos de la fracción.
Operaciones
Simplificación: Simplificar una fracción es hallar otra equivalente que sea irreducible.

Reducción de fracciones a común denominador: Reducir varias fracciones a común

denominador es hallar otras fracciones equivalentes a ellas, cuyos denominadores son
iguales. Si este denominador común es el menor de todos los posibles, se dice que es el
mínimo común denominador. Para reducir varias fracciones a común denominador basta
con multiplicar los dos términos de cada una por los denominadores de los demás.
Si se desea reducir a mínimo común denominador bastará con hallar el mcm (mínimo
común múltiplo) de los denominadores, que será el denominador común, para hallar los
numeradores se divide el mcm por cada uno de los denominadores y se multiplica el cociente por
el numerador correspondiente.
Suma: En la suma de los números racionales pueden darse los casos:

3 7
a) Sumar números racionales del mismo denominador:
5 5
3 7
b) Sumar fracciones con denominadores que sean números primos entre sí. para ello se
5 11
deben reducir a común denominador y luego se efectúa la suma.
3 7 13
c) Sumar fracciones cuyos denominadores no sean primos.
6 2 12
Diferencia: Se llama diferencia de números racionales a la suma del minuendo con el

opuesto del sustraendo. Si decimos restar números racionales de distinto denominador,
bastará con hallar su mínimo común denominador. Si los números racionales tienen el
mismo denominador, su resta se efectúa sumando al minuendo el opuesto del sustraendo y
se deja el mismo denominador.
Multiplicación: La multiplicación de dos números racionales es otro número racional, cuyo

numerador es el producto de los numeradores y cuyo denominador es el producto de los
denominadores. Siempre que sea posible, conviene simplificar antes de multiplicar. Si hay
racionales negativos en la multiplicación, es necesario multiplicar sus signos, aplicando las
leyes de los signos.
Cociente: Para dividir dos números racionales, bastará con multiplicar el primero por el
inverso del segundo.
Potencia: Para hallar la potencia de un número racional se elevan a dicha potencia los dos
términos.
a) También se verifica que la potencia cero de un número racional distinto de cero es 1.

b) La potencia primera de un número racional es el mismo racional.
c) Puede ocurrir que el número racional esté elevado a un exponente negativo. Este caso no se
había presentado nunca porque siempre elevábamos a exponentes naturales. Y para
resolverla, se eleva el inverso de dicho número racional a una potencia de igual valor
absoluto a la dada, pero con exponente positivo.

4.3.4 Propiedades
El conjunto de números racionales está integrado por parejas de números enteros cuyos
elementos se dividen entre sí. A este conjunto también pertenece el 0 (cero), que está definido por
todas aquellas fracciones que tienen al 0 por numerador.
Los racionales serán positivos o negativos según sea el signo de cada uno de los integrantes
de las parejas que los definen. Así será que parejas de enteros de igual signo definirán un racional
positivo; y parejas de enteros de distinto signo definirán un racional negativo.
No existen racionales cuyo denominador sea 0.
Propiedades generales.
1) Si los dos términos de una fracción se multiplican por un mismo número entero, la fracción
resultante es equivalente a la primera y representa, por lo tanto, el mismo número natural.
Consecuencia: siempre es posible representar un número racional por una fracción de

denominador positivo, ya que si fuera negativa, bastaría con multiplicar por –1 los dos
términos de la fracción.
2) Si los dos términos de una fracción tienen un divisor común y se dividen por él, la fracción
resultante es equivalente a la primera.
Consecuencia: Un número natural puede representarse por una fracción cuyos dos términos
son primos entre sí (basta con dividirlos por su máximo divisor común). Una fracción de
este tipo se llama irreducible y es representante canónico del número racional.
3) Densidad del orden: Dados dos números racionales distintos, a<b, siempre existe otro
número racional c tal que a<c<b.
u p u p
Para ello, si a y a , con v y q positivos, basta con tomar c .
v q v q
Propiedades de la suma
La suma de números racionales goza de las mismas propiedades que la suma de números
naturales y enteros. Es decir, cumplen las propiedades de cerradura, conmutativa, asociativa,
tiene el elemento neutro, existe el opuesto de todo elemento, esto es, el inverso y cumple además
la propiedad uniforme.
a) Cerradura: La suma de números racionales es un número racional.
b) Conmutativa: El orden de los sumandos no altera el valor de la suma.
c) Asociativa: En una suma de números racionales pueden sustituirse dos o más sumandos por
su suma ya efectuada, no variando la suma total.

d) Elemento neutro: El conjunto de los números racionales existe un número que, sumando a
cualquier otro, da siempre este otro. A este número se le llama elemento neutro de la suma
3 0 9 3
y es el cero. Por ejemplo:
4 6 12 4
e) Existencia del inverso: El inverso u opuesto de un número racional es su negativo. La suma

de un número y su opuesto es cero.
f) Uniforme: La suma de números racionales no depende de las fracciones elegidas para

representarlos.
Propiedades de la multiplicación o producto

El producto de números racionales cumple las propiedades enunciadas para los números
enteros, estas son: cerradura, conmutativa, asociativa, elemento neutro, elemento inverso y la
propiedad uniforme.
a) Cerradura: El producto de números racionales es un número racional.
b) Conmutativa: El orden de los factores no altera el producto.
c) Asociativa: En un producto de números racionales pueden sustituirse dos o más factores

por el producto efectuado.
d) Elemento neutro: En el conjunto de los números racionales existe un número que,

multiplicado por cualquier otro, da siempre este otro. A tal número se le llama elemento
a
neutro respecto del producto. Es el representado por las fracciones de tipo (numerador y
a
denominador iguales).
e) Elemento inverso: Es aquél que, multiplicado por un número racional, hace que su
2 5
producto sea el elemento neutro. Por ejemplo, para , su inverso es . Dos números
5 2
racionales que tienen numerador y denominador respectivamente iguales al numerador y
denominador del otro se dicen inversos. Convenimos en no escribir el denominador 1. El 0
no tiene inverso.
f) Distributiva: Para aplicarla, se procede así: el factor se multiplica por cada término de la
suma algebraica, aplicando la regla de los signos; por último se efectúa la suma algebraica
indicada.
g) Uniforme: El producto de números racionales no depende de las fracciones elegidas para

representarlo.

4.6 LOS NUMEROS REALES
Los números reales comprenden los números naturales, los números enteros, los números
racionales y los números irracionales, son más amplios que los números racionales ya que
incluye también números que no están formados por parejas de enteros. Surgen ante la necesidad
de solucionar problemas como: determinar, en Q, la solución de la ecuación x2–2=0, la cual no
existe en este conjunto, porque no existe un número racional cuyo cuadrado sea igual a 2. El
conjunto de los números reales se designan con la letra R.
Operaciones
Con los números reales, sumamos, restamos, multiplicamos, dividimos, determinamos la
potencia de un número y determinamos la raíz de un número; estas constituyen las operaciones
principales en los números reales.
Suma: La suma de números reales, también llamada adición, es una operación que se
efectúa entre dos números, pero se pueden considerar también más de dos sumandos.
Siempre que se tengan dos números reales, se pueden sumar entre sí.
Resta: La resta es la operación inversa de la suma, es una operación entre dos números: el
minuendo y el sustraendo. Siempre que se tengan dos números reales, se pueden restar. Al
efectuar restas hay que tener cuidado con los signos de los números. Las siguientes reglas
pueden recordarle cómo es esto:
a) Si el minuendo y el sustraendo son positivos, y el minuendo es mayor que el sustraendo, se

efectúa la resta y el resultado es positivo. Por ejemplo: 28.7–11.2=17.5.
b) Si el minuendo y el sustraendo son positivos, y el minuendo es menor que el sustraendo, se
efectúa la resta y el resultado es negativo. Por ejemplo: 11.2–28.7=–17.5
c) Si el minuendo es negativo y el sustraendo es positivo, se efectúa la suma de ambos
números y al resultado se le pone el signo menos. Por ejemplo: –28.1–11.2=–39.3.
d) Restar un número positivo es lo mismo que sumar un número negativo.
Por ejemplo: 28.7–11.2=28.7+(–11.2)=17.5.
e) Restar un número negativo es lo mismo que sumar un número positivo.
Por ejemplo: 28.7–(–11.2)=28.7+11.2=39.3.
Multiplicación o producto: La multiplicación de números reales es una operación que se

efectúa entre dos números, pero se pueden considerar también más de dos factores. Siempre
que se tengan dos números reales, se pueden multiplicar entre sí. Al efectuar
multiplicaciones hay que tener cuidado con los signos:
a) La multiplicación de dos números de igual signo siempre es positivo.
b) La multiplicación de dos números de distinto signo siempre es negativo.
División: La división es la operación inversa de la multiplicación, es una operación entre

dos números: el dividendo y el divisor. Con una excepción, siempre que se tengan dos

números reales, se pueden dividir. La excepción es que el divisor no puede ser cero. Esto
es, no se puede dividir entre cero. Observe que el dividendo sí puede ser cero, y cuando
esto ocurre el resultado o cociente siempre es cero.
Las reglas de los signos en el caso de la división son las mismas que para la multiplicación:
a) La división de dos números de igual signo siempre es positivo.
b) La división de dos números de distinto signo siempre es negativo.
Potencias y raíces: Elevar un número real a una potencia equivale a multiplicarlo por sí
mismo tantas veces como indica el exponente.
La operación inversa es la raíz, que puede ser cuadrada, raíz tercera, cuarta o quinta, etc.
La raíz más utilizada es la raíz cuadrada. La raíz cuadrada de un número a es el número que
elevado al cuadrado da a. Cuando se usa raíz cuadrada no se suele poner el 2 arriba del
símbolo. No todos los números reales tienen raíz cuadrada. Todos los números reales
positivos y el cero tienen raíz cuadrada, pero no se puede calcular la raíz cuadrada de un
número negativo
4.4.6 Propiedades
Propiedades de la suma
a) Conmutativa: La expresión usual de esta propiedad es: "el orden de los sumandos no altera
la suma". Si a y b son dos números reales, la conmutatividad se puede expresarse a+b=b+a.
b) Asociativa: Si se tienen más de dos sumandos, da igual cuál de las sumas se efectúe
primero. Si a, b y c son tres números reales, la asociatividad dice que: a+(b+c)=(a+b)+c.
Como da igual en qué orden se efectúen las sumas, lo usual es prescindir de los paréntesis,
y marcar sólo a+b+c.
c) Elemento neutro. El número real 0 sumado a cualquier número lo deja sin cambio: si a es
un número real, entonces a+0=a.
d) Elemento inverso. Todo número real tiene un inverso aditivo, lo que quiere decir que si se
suman el número y su inverso, el resultado es 0: si a es un número real, entonces a+(–a)=0.
Propiedades de la resta
Aunque la resta está muy emparentada con la suma, no tiene todas las propiedades de la
suma. Por ejemplo, la resta no es una operación conmutativa. Consideramos que la resta tiene las
mismas propiedades que la suma, excepto la conmutativa.
Propiedades de la multiplicación o producto

La multiplicación tiene las siguientes propiedades:
a) Conmutativa. La expresión usual de esta propiedad es: "el orden de los factores no altera el
producto". Si a y b son dos números reales, la conmutatividad se puede expresarse como
a b=b a.

b) Asociativa. Si se tienen más de dos factores, da igual cuál de las multiplicaciones se efectúe
primero. Si a, b y c son tres números reales, la asociatividad dice que: a (b c)=(a b) c.
Como en el caso de las sumas, da igual en qué orden se efectúen las multiplicaciones, y por
eso lo usual es prescindir de los paréntesis. Cuando se usan letras, se marca sólo a b c, o
bien, para evitar que el signo se confunda con la letra x, se marca abc, o bien se usa un
punto en vez de la cruz: a·b·c. Es también común prescindir del signo cuando se señalan
productos con los números entre paréntesis: por ejemplo, en vez de escribir (–5) (–3),
podemos escribir (–5)(–3), y en vez de escribir 3 4 podemos escribir 3(4). Es decir, cuando
no se señala ninguna operación entre dos números, se efectúa una multiplicación.
c) Elemento neutro. El número real 1 (uno), multiplicado a cualquier número lo deja sin
cambio: si a es un número real, entonces: a 1 = a.
d) Elemento inverso. Todo número real distinto de cero tiene un inverso multiplicativo, lo que
quiere decir que si se multiplican el número y su inverso, el resultado es 1: si a es un
1
número real distinto de cero, entonces a 1
a
Propiedades de la división
Al ser la división la operación inversa de la multiplicación, cumple las propiedades de
ésta, pero no todas, por ejemplo, la división no es una operación conmutativa.
4.4.7 EXPANSION EN BASE B DE UN NÚMERO REAL
Cuando consideramos los números enteros, se presento la expansión en base b de un

número entero, así como las diferentes bases, la conversión del sistema decimal a otro sistema y
la conversión de otro sistema numérico al sistema decimal.
Para la expansión en base b de un número real, primero consideraremos la representación

decimal del número y posteriormente realizaremos la expansión en base b. Así cuando nos
refiramos a un número real, consideraremos su representación como número decimal.
Sistema de numeración decimal

En este sistema un número real se representa como …S 5 S4 S3 S2 S1 S0.S– 1 S – 2 S– 3 S– 4… ,
en el que Si es uno de los símbolos que usamos en este sistema de numeración, también es
posible representar el número en términos de la base, en este caso en términos de la base 10.
Ejemplo 4.4.1
El número 523.245 es un número real.
En base 10 se representa
523.245=5 102+2 101+3 100+2 10–1+4 10–2+5 10– 3.
La representación de un número real en base 10 es:

N10=..+S4 104+S3 103+S2 102+S1 101+S0 100+S–1 10–1+S–2 10–2+S–3 10 –3+S–4 10–4+…

Donde cada Si es un símbolo cualquiera de los 10 que se consideran en este sistema y

donde el subíndice de S coincide con el exponente del 10. Esta representación se denomina
expansión en base 10 de un número real.
Otros sistemas de numeración

La forma común general, para representar cualquier número real en todas las bases, es:
NB=...+ S4 B4+S3 B3+S2 B2+S1 B1+S0 B0+S–1 B–1+S–2 B–2+ S– 3 B–3+S–4 B– 4+…
Donde B es la base del sistema y los Si son símbolos del sistema considerado.
Esta representación de cualquier número real (con su representación en decimal), se

denomina expansión en base B de un número real.
Conversión de un sistema decimal a otro sistema numérico

El proceso de conversión de un número real en sistema decimal a otro sistema de
numeración, se realiza de la siguiente forma:
1) Se separa la parte entera de la parte decimal o fraccionaria.
2) La conversión de la parte entera es igual a la conversión de un número entero en base

decimal a otra base, esto es, se basa en la realización de divisiones sucesivas; dividiendo
primero el número entero entre la base, el residuo es S0 ; luego, el cociente se divide entre la
base, el residuo es S1; así continuamos hasta obtener un cociente menor que la base, este
cociente es el último Si.
3) La parte fraccionaria se multiplica por la base del número deseado. Se separa la parte entera
del número del producto y se designa con S–1 . Seguidamente, la parte fraccionaria del
nuevo producto se multiplica por la base y la parte entera de este producto es la segunda
cifra del a fracción en la base deseada. Se repite este proceso de multiplicación de las partes
fraccionarias de los sucesivos productos por la base deseada; después de realizar cada
multiplicación, se separa la parte entera del producto para que sirva de nuevo dígito S, hasta
que ocurra una de dos cosas: (a) la parte fraccionaria del producto es exactamente igual a
cero, o (b) los dígitos de la fracción comienzan a repetirse, todos a partir de alguno, en
grupos iguales llamados períodos.
Ejemplo 4.4.2
Representar el número 45.65 en base 4.
Primero consideramos la parte entera, esta es 45 y la representamos en base 4
11 2
4 45 4 11 (S2) 4510 = 2314
1 3
S0 S1
4510=2314
La parte fraccionaria es 0.65
0.65 4=2.6 parte entera=2 y parte fraccionaria=0.6 S–1=2.


0.4 4=1.6 parte entera = 1 y parte fraccionaria=0.6 S–7=1.
Así, 0.6510=22121214= 221 , donde la barra sobre el número 21 nos indica el período, es
decir que este se repite.
Luego 45.6510=231. 221 4.
Conversión de otro sistema numérico al sistema decimal

Para realizar la conversión de un número real en cualquier base (diferente de 10), a la base
10, se representa el número con la expansión en la base b y se simplifica usando la aritmética
decimal.
Ejemplo 4.4.3
Convertir el número 7412.653 8 a base decimal.
Expresamos el número 7412.653 8 en expansión de la base 8.
7412.6538=7 83+4 82+1 81+2 80+6 8–1+5 8–2+3 8–3.

=7 512+4 64+1 8+2 1+6 0.125+5 0.015625+3 0.001953125.
=3584+256+8+2+0.75+0.078125+0.005859375.
=3850.833984375.
Ejercicios: Unidad IV
4.1 Mostrar que las propiedades siguientes son válidas para los enteros positivos.
n
a) 4i 2n(n 1)
i 1
10n(n 1)
b) 10+20+30+...+10n=
2
n
n(2n 1)( 2n 1)
c) (2i 1)2
i 1 3
n n 1
a 1
d) ai para a 1
a 0 a 1
n
n(n 1)( 2n 1)
e) i2
i 1 6
n
n(n 1)( n 2)
f) i(i 1)
i 1 3
n 2
3 n(n 1)
g) i
i 1 2

n
h) i(i!) (n 1)! 1
i 1
n
[( 1) n 1 n(n 1)]
i) ( 1) i 1 i 2
i 1
2
n
1 n
j)
i 1 ( 2i 1)( 2i 1) 2n 1
n
n(3n 1)
k) (3i 2)
i 1 2
n
l) 9 10 i 1
10 n 1
i 1
n
m) (2i 1) n2
i 1
n
1 3 1 1
n) 2
i 1 (i 1) 1 4 2(n 1) 2(n 2)
n
n(3n 1)
o) (3i 1)
i 1 2
4.2 Demostrar las siguientes desigualdades

1 1 3 5 ... (2n 1)
a) para n=1,2,…
2n 2 4 6 ... (2n)
b) 2n+1 2 n para n=3,5,…
c) 2 n n 2 para n=4,5,…
d) 2 n n! para n 4
e) 2 n 2n 1
2n 1
1 para n=1,2,…
1 1 1 1 1 1
f) 1 1 1 ... 1 para n=1,2,…
2 4 8 2n 4 2 n 1
g) 2(n+2) (n 2) 2 para n=1,2,…
h) 2n+1 2n para n 3
i) n!>2 n 1
para n 3
j) n n 2n n ! para n 3

k) n2 2n+1 para n=3,4,5,…
l) (1+x)n 1+nx para n=1,2,3,…y x≠–1.
4.3 Demostrar las siguientes proposiciones
a) 7 n 2n es divisible por 5 para n=1,2,…
b) 7 n 1 es divisible por 6 para n=1,2,…
c) 11 n 6 es divisible por 5 para n=1,2,…
d) 6 7n–2 3n es divisible por 4 para n=1,2,…
e) 3 n 7 n 2 es divisible por 8 para n=1,2,…
f) n7–n es divisible por 7 para n=1,2,…
g) 4 n +15n–1 es divisible por 9 para n=1,2,…
h) 11 n 2 +12 2n 1 es divisible por 133 para n=1,2,…
4.4 Demostrar que a b (mod m) si y sólo si m|a.
4.5 Demostrar que para a, b, c en Z se tiene que
a) Si a b (mod m) entonces ac bc (mod m).

b) Si a+c b+c (mod m), entonces a b (mod m).
c) Si ac bc (mod m) y si m y c son primos entre sí, entonces a b (mod m).
4.6 Convertir a binario los números decimales.

a) 49
b) 0.375
c) 75.125
4.7 Realizar las conversiones indicadas

a) 1010001 de base 2 a base 10
b) 1398 de base 10 a base 8
c) FAB de base 16 a base 10
d) 18.287 de base 10 a base 16
e) 100100010100 de base 2 a base 10
f) 96 de base 16 a base 10
g) 26419 de base 10 a base 16

4.8 Convertir los siguientes números decimales a la base indicada.

a) 12.345 a base 2
b) 45.897 a base 3
c) 89076.985 a base 6
d) 123456. 9876 a base 8
e) 12340987. 4588929 a base 16
Unidad V: Teoría de grafos
5.1. Definiciones básicas de grafos.

5.1.1 Grafos y digrafos.
5.1.2 Grado interior y exterior de un vértice.
5.1.3 Representación de un grafo.
5.2 Caminos y circuitos.

5.2.1 Definiciones básicas.
5.2.2 Grafos conexos.
5.2.3 Circuitos Eulerianos.
5.2.4 Ciclos Hamiltonianos.
5.3 Árboles.
5.3.1 Árboles enraizados.
5.3.2 Árboles binarios y n-arios.
5.4. Un algoritmo del camino más corto.
5.5 Isomorfismos de grafos.
5.6 Grafos planos.
5.1 DEFINICONES BÁSICAS DE GRAFOS
5.1.1 Grafos y digrafos
Consideremos el siguiente problema.
En la siguiente figura se muestra el mapa de un sistema eléctrico, este sistema debe ser
inspeccionado por un electricista, el electricista debe analizar cada uno de los cables y
proporcionar un informe sobre las condiciones de los mismos. La manera más rápida de
inspeccionar todo el sistema será comenzar en una conexión, recorrer todos los cables
exactamente una vez y terminar en el punto de inicio. ¿Es esto posible?

Fig 5.1.1 Sistema eléctrico
Este problema se soluciona haciendo uso del concepto matemático que llamamos grafo o
gráfica. Veamos las nociones básicas de este concepto y luego podremos regresar al problema
planteado.
Definición 5.1.1 (Grafo)

Un grafo o grafo no dirigido (llamado también gráfica) consta de un conjunto V de vértices
o nodos y de un conjunto E de aristas, arcos o lados, tales que cada arista e E 2queda asociada a
un par no ordenado de vértices. Si existe una única arista e asociada con los vértices v y w,
escribimos e=(v,w) o e=(w,v). En este contexto (v,w) denota una arista entre v y w en un grafo no
dirigido y no un par ordenado. Denotamos al grafo G de vértices V y arista E como: G=(V,E).
De la definición dada notamos que un grafo queda determinado por un conjunto de vértices
y por un conjunto de aristas así, gráficamente un grafo queda determinado también en función de
estos dos conjuntos; el conjunto de vértices lo representamos por puntos y el conjunto de aristas
lo representamos por líneas (arcos). El siguiente ejemplo nos muestra un grafo representado
tanto analíticamente como gráficamente.
Ejemplo 5.1.1
a) Sea G un grafo determinado por los siguientes conjuntos
V={a,b,c,d,e} y E={(a,b), (a,e), (b,c), (c,a), (c,e), (d,a), (d,b), (e,b)}
El grafo G se muestra de manera gráfica en la siguiente figura.
Fig. 5.1.2
b) Otro ejemplo de un grafo no dirigido es el mapa de la ciudad que muestra sólo las calles de
doble sentido, donde
 Los nodos (o vértices) son las intersecciones de las calles.
2
Denotada por e debido a su nombre en ingles edge.

 Las aristas (o lados) son las calles de doble sentido.
Otro concepto básico en teoría de grafos es el de digrafo, el cual se define a continuación.
Definición 5.1.2 (digrafo)

Un grafo dirigido o digrafo G, está formado por un conjunto V de vértices y un conjunto E
de aristas, tales que cada arista e E se asocia con un par ordenado de vértices.
Si existe una única arista e asociada con el par ordenado (v,w) de vértices escribimos
e=(v,w), lo cual denota la arista de v a w. El digrafo G de vértices V y aristas E se denota de la
misma manera que el grafo G de vértices V y aristas E, esto es G=(V,E).
Gráficamente se representa a un digrafo de un modo semejante a un grafo, la diferencia

entre el grafo y el digrafo está en que en el digrafo se agregan dirección a los arcos, esto es, serán
flechas. Un digrafo se muestra en el siguiente ejemplo:
Ejemplo 5.1.2
Sea G un digrafo determinado por los conjuntos
V={1,2,3,4,5} y E={(1,2), (1,3), (1,5), (2,3), (3,1), (3, 4), (4,1), (4,3), (5,2)}
Con la siguiente representación gráfica.
Fig. 5.1.3
Examinando los ejemplos dados para un grafo y un digrafo vemos que la diferencia entre
ellos se presenta en la dirección de las aristas, notando también que en la representación analítica
de un grafo no aparecen dos parejas ordenadas con los mismos elementos mientras que el digrafo
si las hay y nos representan aristas diferentes.
En lo siguiente cuando nos refiramos a un grafo no dirigido usaremos el término grafo y

para referirnos al grafo dirigido usaremos el término digrafo.
Hay algunos conceptos que se destacan en las definiciones de grafos y digrafos.

Presentamos estos conceptos en la siguiente definición.
Definición 5.1.3
Sea G=(V,E) un digrafo.
a) (Vértices adyacentes o vecinos)

Decimos que los vértices v y w son adyacentes o vecinos si existe una arista e asociada con
el par de vértices v y w. Decimos además que e es incidente en v y w o bien que los vértices
v y w son incidentes en e.
b) (Aristas paralelas)
Las aristas e1 y e2 son paralelas si están asociadas al mismo par de vértices, esto es, las
arista e1 y e2 son incidentes a los vértices v y w.
c) (Lazo)
La arista e se denomina lazo si es incidente en un único vértice.
d) (Vértice aislado)
Es un vértice que no es incidente a ninguna arista.
e) (Grafo simple)
Si G no tiene aristas paralelas y no tiene lazos se denomina grafo simple.
Ejemplo 5.1.3
Considere el siguiente digrafo.
Fig. 5.1.4
a) Los pares de vértices a b; a,c; a,e; b,c; c,e; c,d; d,d; e,c y e,d; determinan una arista, así
decimos que cada pareja de vértices son incidentes, son adyacentes o son vecinos.
b) Las aristas e1=(c,e) y e2=(e,c) son aristas paralelas ya que los mismos vértices determinan
aristas diferentes.
c) La arista e3=(d,d) representa un lazo ya que es incidente en un solo vértice. Y,
d) f representa un vértice aislado ya que no tiene vértices incidentes en él.
Estos conceptos también se aplican a los grafos, salvo el de aristas paralelas ya que en un
grafo no hay aristas diferentes asociadas a un mismo par de vértices.
Ejemplo 5.1.4
La figura muestra un grafo simple, observemos que no tiene aristas paralelas ni lazos.

Fig. 5.1.5
Definición 5.1.4 (Grafo completo de n vértices)

El grafo que tiene n vértices y cada vértice es adyacente a todos los demás (sin lazos ni
lados paralelos), se denomina grafo completo de n vértices y se denota por K n.
Ejemplo 5.1.5
Los siguientes grafos representan a K3 y K4 .
Fig. 5.1 6 K3 Fig 5.1.7 K4
Definición 5.1.5 (Grafo bipartido)

Se dice que G es un grafo bipartido si G=(V,E) es un grafo tal que V=V1 V2 y V1 V2= ,
y además todo lado e E es incidente a un vértice de V1 y a uno de V2.
Definición 5.1.6 (Grafo bipartido completo de m+n vértices)

Km,n es un grafo bipartido completo de m + n vértices si es bipartido (sin lados paralelos)
tal que |V1 |=m, |V2 |=n y todo vértice de V1 es adyacente a todo vértice de V2 .
Ejemplo 5.1.6
Considere el siguiente grafo.
Fig. 5.1.8 K2,2

Sean V={a,b,c,d} y E={e1,e2 ,e3,e4}

Si V1={a,b} y V2={c,d) se tiene que V=V1 V2 y V1 V2= .
e1 es incidente en a y c.
e2 es incidente en a y d.
e3 es incidente en b y d.
e4 es incidente en b y c en consecuencia todo lado e E es incidente a un vértice de V1 y a
uno de V2 . Por lo tanto el grafo es bipartido.
Además observe que |V1 |=2, |V2 |=2 y todo vértice de V1 es adyacente a todo vértice de V2 ,
por lo tanto, es un grafo bipartido completo de 4 vértices, K2,2.
5.1.2 Grado interior y exterior de un vértice
Definición 5.1.7 (grado de un vértice)

Sea G=(V,E) un grafo o un digrafo, el grado de un vértice v V es igual al número de
aristas incidentes en v, y se denota por grad (v).
En particular para un lazo consideramos que se tienen dos aristas incidentes, por lo que el
grado de un lazo es de dos, y que un vértice aislado no tiene aristas incidentes por lo que el grado
de un vértice aislado es cero.
Otros conceptos relacionados con el grado de un vértice se presentan en la definición

siguiente:
Definición 5.1.8
Sea G = (V, E) un digrafo.
a) (grado de entrada de un vértice)
El grado de entrada o grado interior de un vértice v es el número de aristas de G que llegan
a v y se denota por ge (v).
b) (grado de salida de un vértice)
El grado de salida o grado exterior de un vértice v es el número de aristas de G que parten
de v y se denota por gs (v).
Ejemplo 5.1.7
Consideremos el siguiente digrafo

Fig. 5.1.9
Grados de entrada grados de salida grados del vértice

ge(a)=0 gs(a)=4 grad(a)=4
ge(b)=3 gs(b)=0 grad(b)=3
ge(c)=0 gs(c)=4 grad(c)=4
ge(d)=3 gs(d)=2 grad(d)=5
ge(e)=1 gs(e)=2 grad(e)=3
ge(f)=6 gs(f)=1 grad(f)=7
ge(g)=2 gs(g)=2 grad(g)=4
Observe que un lazo tiene un grado de salida y un grado de entrada, hay vértices que solo
tienen grado de entrada o bien de salida, y algo más importante que la suma de los grados de
entrada y de salida es el grado del vértice. En general en grafos sólo se considera el grado de
vértice y los grados de entrada y de salida se usan para los digrafos.
5.1.3 Representación de un grafo
Un grafo se ha representado por medio de un diagrama. Sin embargo cuando se quiere

analizar un grafo por medio de una computadora, esta representación no es muy útil. Otras
formas de representar un grafo es por medio de la matriz de adyacencia y la matriz de incidencia.
Representación de un grafo por medio de la matriz de adyacencia
Para representar un grafo por medio de una matriz de adyacencia se pueden seguir los
siguientes pasos:
1) Se selecciona un orden arbitrario para los vértices.

2) Se le asigna a las filas y a las columnas el mismo orden dado a los vértices.
3) Un elemento de la matriz es 1 si los vértices correspondientes a la fila y a la columna de
dicho elemento están unidos por una arista y 0 en otro caso.
Ejemplo 5.1.8
Considere el siguiente grafo
Fig. 5.1.10

Se selecciona un orden arbitrario para los vértices, por ejemplo a, b, c, d, e, y f. La matriz

de adyacencia que representa este grafo es:
a b c d e f
a 0 1 0 0 0 0
b 1 0 1 0 1 1
c 0 1 1 0 0 1
d 0 0 0 0 1 0
e 0 1 0 1 0 0
f 0 1 1 0 0 0
Observe que la matriz de adyacencia permite representar los lazos pero no permite
representar las aristas paralelas.
Ejemplo 5.1.9
Considere el siguiente grafo
Fig. 5.1.11
Se selecciona un orden arbitrario para los vértices, por ejemplo a, b, c, d, e, y f. La matriz

de adyacencia que representa este grafo es:
a b c d e
a 0 1 0 1 0
b 1 0 1 0 1
c 0 1 0 1 1
d 1 0 1 0 1
e 0 1 1 1 0
Observe que este grafo no tiene lazos y se puede obtener el grado de un vértice sumando
la fila o la columna correspondiente, por ejemplo el gr(a)=2, gr(b)= , etc.
Representación de un grafo por medio de la matriz de incidencia

Para representar un grafo por medio de una matriz de incidencia se pueden seguir los
siguientes pasos:
1) Se asignan a las filas las marcas correspondientes a los vértices.

2) Se asignan a las columnas las marcas correspondientes a las aristas.
3) El elemento correspondiente a la fila v y a la columna e es 1 si e es incidente en v, y es 0 en
cualquier otro caso.
Ejemplo 5.1.10
Considere el grafo de la figura 5.1.6.
Fig. 5.1.12
La matriz de incidencia que representa este grafo es:

e1 e2 e3 e4 e5 e6 e7
a 1 0 0 0 0 0 0
b 1 1 0 1 1 0 0
c 0 1 1 0 0 1 0
d 0 0 0 0 0 0 1
e 0 0 0 1 0 0 1
f 0 0 0 0 1 1 0
Una columna con un solo uno como la de e3, representa a un lazo.
Ejemplo 5.1.11
Fig. 5.1.13
La matriz de incidencia que representa este grafo es:

e1 e2 e3 e4 e5 e6 e7
a 1 1 0 0 0 0 0
b 1 0 1 0 0 1 0
c 0 0 1 1 1 0 0
d 0 1 0 1 0 0 1
e 0 0 0 0 1 1 1
Observe que la matriz de incidencia permite representar tanto lados paralelos como lazos.
Nótese que en un grafo sin lazos cada columna tiene dos unos y que la suma de cada fila da el
grado del vértice correspondiente, por ejemplo en el caso de la figura 5.1.9, el grado del vértice c
es tres y la suma de las cifras de la fila correspondiente a c también es 3.
5.3 CAMINOS Y CIRCUITOS
5.3.1. Definiciones básicas.
Otro concepto básico en teoría de grafos es el de camino, el cual se define a continuación.
Definición 5.2.1 (Camino)

Sean v y w dos vértices no necesariamente distintos de un grafo no dirigido G=(V,E). Un
camino v–w en G es una sucesión alternada 3 finita (sin lazos)
v=v1, e1, v2, e2 , v3, e3 , . . . , en-1, v n-1, en, v n=w
de vértices y aristas de G que comienza en el vértice v y que termina en el vértice w, que contiene
además n aristas ei={vi,vi+1} donde 1 i n.
Con frecuencia en un grafo la sucesión de lados, v=v1, e1, v2, e2, v3 , e3, . . . , en-1 , v n-1, en,
vn=w, se puede escribir como:
{(v1,v2), (v2,v3), (v3,v4) ,…, (v n-1 ,v n)}, y se puede abreviar como (v1 , v2, v3, … , v n-1 , v n), o bien
(e0 , e1 , e2 ,...en ) .
Definición 5.2.2
a) La longitud de un camino es igual al número de aristas que integran el camino.
b) Si n=0, no existe arista, v=w, el camino se llama trivial.
c) Cualquier camino v–w donde v=w(y n>1) se llama camino cerrado; en caso contrario
decimos que el camino es abierto.
Obsérvese que en el camino se pueden repetir vértices y aristas.
Ejemplo 5.2.1
3
Consideramos una sucesión alternada a una lista que con elementos que se presentan de un modo alternado

Considere los caminos del siguiente grafo
Fig. 5.2.1
a) (a,b,d,c,e,d,b), es un camino abierto desde a hasta b de longitud n=6, en este camino se

repiten los vértices b y d y la arista e4=(b,d)=(d,b).
b) (b,c,d,e,c,f), es un camino abierto desde b hasta f de longitud n=5, en este camino se repite
el vértice c y no se repite ninguna arista.
c) (f,c,e,d,a), es un camino abierto desde f hasta a de longitud n=4, en este camino no se

repiten vértices ni aristas.
d) (b,c,d,b), es un camino cerrado desde b hasta b de longitud n=3, en este camino no se

repiten vértices ni aristas.
Ejemplo 5.2.2
Sea G el grafo determinado por el conjunto V de vértices y el conjunto E de aristas.
V={1,2,3,4,5,6,7} y E={(1,2), (2,3), (2,4), (2,5), (3,4), (5,6), (2,6), (6,7)}
encontrar un camino de 1 a 7.
Fig. 5.2.2
Los siguientes son caminos desde el vértice 1 hasta el vértice 7.

a) (1,2,6,7).
b) (1,2,5,6,7).
c) (1,2,3,4,2,5,6,7).
Todos ellos nos dan una solución al problema planteado pero observamos que tienen
diferente longitud, el primero de ellos tiene longitud 3, el segundo 4 y el tercero 7. Con lo cual
notamos que la determinación de un camino v–w no es única.

Hay algunos otros conceptos para grafos referidos a un camino, estos se presentan en la
siguiente definición:
Definición 5.2.3: Consideremos un camino de x a y (x–y) en un grafo no dirigido G=(V, E).

a) Un recorrido es un camino abierto de x a y en el cual no se repite ninguna arista.
b) Un circuito es un camino cerrado de x a x en el cual no se repite ninguna arista.
c) Un camino simple es un camino abierto de x a y en el cual no se repite ningún vértice.
d) Un ciclo es un camino cerrado de x a x en el cual sólo se repite el vértice x.
Ejemplo 5.2.3
Determine como se llaman los caminos del ejemplo 5.2.1.
a) ninguno
b) recorrido
c) recorrido, camino simple
d) circuito, ciclo.
5.2.5 Grafos conexos
Definición 5.2.4 (Grafo conexo)

Un grafo G es conexo si dados cualesquiera dos vértices v y w en G, existe un camino de v
a w. Un grafo es conexo si no tiene vértices aislados.
Ejemplo 5.2.4
a) Sea G=(V,E) como el grafo de la figura 5.2.2. El grafo es conexo, ya que es posible
determinar uno (o varios) camino entre 1 y 7 y de la misma manera sucede con cualquier
par de vértices.
b) El grafo representado en la figura
Fig. 5.2.3
No es conexo, ya que no es posible determinar un camino entre el vértice V4 y el vértice V6

y entre algunos otros vértices.
Con este ejemplo notamos que para que un grafo sea conexo no puede tener vértices
aislados además que, podríamos decir que debe ser de una sola pieza. Si tenemos un grafo que no
es conexo con varias “piezas” podemos decir que cada una de ellas es conexa como sucede aquí
con el triángulo formado por los vértices V1, V2 y V3 y el segmento formado por V5 y V6.

Con todos estos conceptos considerados de teoría de gráficas nos es posible volver al
problema inicial. Recordemos que en él se pregunta si es posible que el electricista inicie en una
conexión, por ejemplo a, recorra todos los cables una sola vez y regrese al punto a. Para
responder a esta pregunta empecemos por considerar el grafo asociado a la situación planteada,
para ello se considera a las conexiones como vértices y los cables como aristas.
Fig. 5.1.4
Al trazar una gráfica la única información importante es saber cuales vértices están unidos
por cuales aristas.
El problema planteado se puede parafrasear de la siguiente forma:

¿Existe un camino cerrado en a que recorra cada arista sólo una vez?
Si intentamos formar caminos cerrados con esta característica veremos que no es posible, lo
más cercano es el repetir una sola arista pero esto no es lo que se pide. Es importante que se
intente encontrar una solución para apreciar que efectivamente no es posible.
5.2.6 Circuitos Eulerianos
Este problema nos introduce en el concepto de camino Euleriano el cual da una razón del
porqué no se puede determinar el camino pedido.
Definición5.2.5 (Circuito Euleriano)

Sea G=(V, E) un grafo conexo. G tiene un circuito Euleriano si existe un circuito en G
que recorra cada arista del grafo exactamente una vez.
Observe que en la definición no se hace referencia a los vértices, esto indica que no importa
si estos se repiten o no.
Ejemplo 5.2.5
Los siguientes grafos tienen un circuito Euleriano.
a)
Circuito Euleriano:
a, e1, b, e3, c, e5,d, e4, b, e6, e, e7, c, e2, a.

Fig. 5.2.5
b)
Circuito Euleriano:
a, e1, b, e4, d, e9, e, e5, b, e2, c, e6, f, e10, e, e14,
j, e15, f, e11, g, e7, c, e8, h, e12, g, e18, l, e20, h,
e19, k, e23, l, e17, f, e16, k, e22, j, e21, i, e13, d,
e3, a.
Fig. 5.2.6
Nota: Observe que cada vértice tiene grado par y se puede construir el circuito desde cualquier
vértice.
¿Si uno o más vértices tienen grado impar se puede construir un circuito Euleriano?
No, porque cada vértice debe tener una entrada y una salida.
Teorema 5.2.1
Un grafo tiene un Circuito Euleriano si y sólo si todos sus vértices tienen grado par.
Este teorema nos da una razón del porque el problema del electricista no tiene solución. En
el grafo que representa el sistema eléctrico dado al inicio de la unidad (ver fig 5.2.4) se tienen dos
aristas de grado impar, por lo tanto el electricista no puede analizar el sistema eléctrico
comenzando en un vértice y terminar en el mismo vértice.
Definición5.2.6 (Recorrido Euleriano)

Sea G=(V,E) un grafo no dirigido conexo. G tiene un recorrido Euleriano, si existe un
recorrido en G que pase por cada arista de V exactamente una vez.
Ejemplo 5.2.6
Los siguientes grafos tienen un recorrido Euleriano.
a)
Recorrido Euleruiano:
e, e4, b, e1, a, e3, d, e11, e, e9, g, e10, f, e7, d, e8, g, e6, c, e2,
b, e5 g.
Fig. 5.2.7

b)
Recorrido Euleriano:
g, e9, d, e5, b, e1, a, e4, g, e11, f, e8, d, e6, c, e7, e, e2, a, e3, f, e10, e.
Fig. 5.2.8
Nota: Observe que sólo dos vértices tienen grado impar.

Teorema 5.2.2
Un grafo tiene un recorrido Euleriano si y sólo si G es un conexo y tiene exactamente dos
vértices de grado impar. Para construir el recorrido Euleriano se debe empezar en un el vértice de
grado impar y se termina en el otro vértice.
Construyendo un recorrido en el sistema eléctrico del problema introductorio a esta unidad

se resuelve el problema del electricista.
5.2.7 Ciclos Hamiltonianos
Definición 5.2.7 (Ciclo Hamiltoniano)

Si G=(V,E) es un grafo con |V| 3, decimos que G tiene un ciclo Hamiltoniano si existe un
ciclo en G que contenga cada vértice de V.
Observe que en la definición no se hace referencia a las aristas, esto indica que no importa
si se pasa o no por todas ellas.
Ejemplo 5.2.7
El siguiente grafo tiene un ciclo hamiltoniano.
Fig. 5.2.9
Ciclos Hamiltonianos:
Fig. 5.2.10
Como puede observar, si un grafo tiene ciclo Hamiltoniano, se pueden construir muchos.
Definición 5.2.8: (Camino Hamiltoniano)

Un camino hamiltoniano es un camino simple de G que contiene todos los vértices.

Ejemplo 5.2.8
El siguiente grafo tiene un camino
Hamiltoniano.
Fig. 5.2.11
Caminos Hamiltonianos:
Fig.5.2.12

Unidad VI: Álgebra booleana y circuitos Propiedades del álgebra booleana
Sugerencias para determinar si un grafo tiene un ciclo Hamiltoniano.

a) Si G tiene un ciclo hamiltoniano, entonces para v V, grad(v) 2.
b) Si a V y grad(a)=2, entonces los dos aristas incidentes en el vértice a deben aparecer en
cualquier ciclo hamiltoniano de G.
c) Si a V y grad(a)>2, cuando tratamos de construir un ciclo hamiltoniano, una vez que
hemos pasado por el vértice a, dejamos de tener en cuenta las aristas no utilizadas
incidentes con a.
d) Si se puede construir un ciclo hamiltoniano se debe cumplir que
|E| - número de aristas no utilizadas=|V|
Ejemplo 5.2.9
Determinar si el siguiente grafo tiene un ciclo hamiltoniano o un camino hamiltoniano.
Fig. 5.2.13
Número de vértices=|V|=11.
Número de aristas=|E|=19.
Observe que los vértices, a, c y k sólo tienen dos aristas, por lo que las dos deben aparecer
en el ciclo Hamiltoniano.
Comenzamos a construir el ciclo partiendo del vértice a.
Vértices a b c g k j f e i h d a
Aristas eliminadas 0 4 0 1 0 1 1 1 0 0 0 0
Total de aristas eliminadas=8
|E|=Número de vértices – total de aristas eliminadas=19–8=11.

Por lo tanto el grafo tiene ciclo hamiltoniano.

Fig. 5.2.14
5.3 ÁRBOLES
Los árboles son una clase especial de grafos. Una de las aplicaciones importantes de los
árboles se da en las ciencias de la computación, en particular, para la organización y ordenación
de datos y las relaciones entre los mismos en una base de datos.
5.3.3 Árboles enraizados.
De manera intuitiva un árbol es una gráfica que se parece a un árbol con sus ramificaciones
hacia abajo.
Definición5.3.1 (Árbol)
Sea G=(V,E) un grafo no dirigido sin lazos. El grafo G es un árbol si G es conexo y no
contiene ciclos.
Un árbol T es un grafo simple que satisface: si v, w son vértices de T, entonces existe un
único camino simple de v a w.
Fig. 5.3.1 Árbol libre
Definición 5.3.2 (Árbol con raíz o radicado)

Si G es un grafo dirigido, entonces T es un árbol dirigido si el grafo no dirigido asociado
con G es un árbol. Si G es un árbol no dirigido, G es un árbol con raíz si existe un único vértice r
en G, llamado la raíz, tal que el grado interior de r es cero, esto es gi(r)=0 y para todos los demás
vértices, el grado interior es 1, esto es, si v es un vértice diferente de r entonces gi(v)=1.
Fig. 5.3.2 Árbol con raíz

El árbol de la figura 5.3.2 se origina del árbol de la figura 5.3.1 al elegir al vértice g como
raíz.

Dado que el camino que va de la raíz a cada uno de los vértices es único, a cada vértice le
corresponde un nivel único. El nivel cero le corresponde a la raíz. A los vértices que están debajo
de la raíz le corresponde el nivel uno, y así sucesivamente. En consecuencia, a la longitud del
camino que va desde la raíz hasta el vértice v se le denomina nivel del vértice v.
Para dibujar un árbol con raíz primero se coloca la raíz en la parte superior. Debajo de la
raíz y en el mismo nivel, se sitúan los vértices que están unidos a la raíz mediante un camino de
longitud 1. Debajo de cada uno de los vértices y en el mismo nivel, se sitúan los vértices que
están unidos a la raíz mediante un camino de longitud 2. Se continúa de esta manera hasta
obtener el dibujo completo del árbol.
Definición 5.3.3 (Altura o peso del árbol)

La altura o peso de un árbol con raíz es el valor de su nivel máximo.
Ejemplo 5.3.1
Considere el árbol de la figura 5.3.2. Los vértices a, b, c, d, e, f, g, h, i y j tienen niveles 3,
3, 2, 1, 2, 2, 0, 1, 2 y 2 respectivamente. El árbol tiene altura 3.
Definición 5.3.4 (Hojas de un árbol)

Las hojas de un árbol son los vértices terminales distintos de r.
Definición 5.3.5 (Vértices internos de un árbol)

Sea T un árbol, los vértices internos de T son los que no son ni hojas ni la raíz del árbol.
Definición 5.3.6 (Vértices adyacentes)

Cada vértice del nivel i es adyacente a exactamente un vértice del nivel i–1 y todos sus
demás vecinos están en el nivel i+1.
Definición 5.3.7
Sea T un árbol con raíz Vo. Supóngase que x, y, z son vértices en T y que (V0 , V1, ..., Vn)
es un camino en T. Entonces:
a) Vn-1 es el padre de Vn.

b) V0 , V1, ..., Vn-1 son los antepasados de Vn.
c) Vn es el hijo de Vn-1
d) Si x es un antepasado de y, entonces y es descendiente de x.
e) Si x y y son los hijos de x entonces x y y son hermanos.
f) Si x no tiene hijos, entonces x es una hoja.
g) Si x no es un vértice terminal entonces x es un vértice interno (o de rama).
h) El subgrafo de T que consiste en x y todos sus descendientes, con x como raíz, es un
subárbol de T radicado en x.
Ejemplo 5.3.2
Considere el árbol con raíz de la figura 5.3.2

a) El padre de c es d.
b) Los antepasados de b son c, d y g.

c) Los hijos de h son i y j.
d) Los descendientes de d son e, f, c, b y a.
e) e, f y c son hermanos.
f) Los vértices terminales son j, i<, e, f, b y a.
g) Los vértices internos son g, h, d y c.
h) El subárbol con raíz en d se muestra en la figura 5.2.3
Fig. 5.3.3
Un árbol con raíz se puede utilizar para especificar relaciones de jerarquía. En este caso, si
un vértice a está en un nivel superior al que corresponde a un vértice adyacente b, entonces a está
“justo arriba” de b y la relación lógica existente entre a y b es: a domina a b, esto es, b es un
subordinado de a. Así por ejemplo el organigrama de la Escuela Superior de Cómputo es un árbol
de jerarquía.
5.3.4 Árboles binarios y n-arios.
Definición 5.3.8 (Árbol binario)

Un árbol binario es un árbol con raíz en el cual cada vértice tiene un hijo a la izquierda o un
hijo a la derecha, o bien ningún hijo.
Definición 5.3.9. (Árbol binario completo)

Es un árbol binario en el cual cada vértice tiene un hijo a la izquierda y un hijo a la derecha,
o bien, ningún hijo.
Ejemplo 5.3.3
a) El grafo de un torneo de eliminación simple es un árbol binario completo. Los equipos
concursantes están a la izquierda y los ganadores siguen a la derecha. Al final hay un
equipo ganador como raíz. Si el número de concursantes no es potencia de 2,
alguno de ellos pasa directamente a la próxima ronda. Las siguientes figuras ilustran un torneo
de eliminación simple con 7 y 8 equipos concursantes.

Fig. 5.3.4 Fig. 5.3.5
b) Si se lanza 3 veces una moneda el número de posibles soluciones se puede representar por
medio de un árbol binario completo, ver figura 5.2.6.
Fig. 5.3.6
Teorema 5.3.1
Si T es un árbol binario completo con i vértices internos, entonces T tiene i+1 vértices
terminales y 2i +1 vértices en total.
Demostración:
Los vértices de T están formados por los vértices hijos de algún padre y por los vértices que
no son hijos de padre alguno. Hay un vértice que no tiene padre, el vértice raíz. Dado que hay i
vértices internos y cada vértice tiene dos hijos, hay 2i hijos. En consecuencia el número total de
vértices de T es 2i + 1, y el número de vértices terminales es el número total de vértices menos el
número de vértices internos, esto es, (2i+1)–i=i–1.
Ejemplo 5.3.4
Si hay 20 equipos concursantes en un torneo de eliminación simple, ¿cuántos partidos
habrá?
Solución
Como este tipo de torneo se puede representar como un árbol binario completo, el número
de participantes es el de vértices terminales, en este caso 20, y el número de partidos i es el
número de vértices internos. Por el teorema 5.3.1 se tiene que el número de vértices terminales es
i+1=20, o bien, i=19.
Definición 5.3.10 (árbol n-ario)

Un árbol con raíz se llama n–ario cuando todos los padres tienen el mismo número de hijos
que es n.
Ejemplo 5.3.5
Si se lanza un dado n veces el número de posibles soluciones puede verse como un árbol
n–ario en este caso n=6.
Definición 5.3.11 (Árbol binario de búsqueda)

Un árbol binario de búsqueda es un árbol binario T en donde se han asociado datos a los
vértices. Los datos se colocan de tal manera que, para cualquier vértice v en T, cada dato en el
subárbol a la izquierda (derecha, respectivamente) de v es menor que (mayor que,
respectivamente) el dato correspondiente a v. Para las palabras comunes se aplica el orden
alfabético.
Ejemplo 5.3.6
Las palabras de la frase “Sólo con el corazón se puede ver bien” se puede colocar en un
árbol binario de de búsqueda como en la figura 5.3.7.
Fig. 5.3.7
La representación de un árbol binario de búsqueda no es única. La frase del ejemplo 5.2.7

también se puede representar como
Fig. 5.3.8
Para localizar un dato en un árbol binario de búsqueda se puede usar el siguiente algoritmo.
Algoritmo 5.3.1 (Localización de un árbol binario de búsqueda)

Sea T un árbol binario de búsqueda con raíz r. Si v es un vértice en T, I(v) indica el hijo a la
izquierda de v y D(v) indica el hijo a la derecha de v. Valor(v) representa al dato asociado al
vértice v.

Para un dato W, el siguiente algoritmo proporciona el vértice v que contiene a W o # si W

no está en el árbol.
Paso 1 Inicialización
P=r.
Paso 2 ¿Dato encontrado?
Si P=#
Terminar “Fracaso: dato no encontrado”
En caso contrario
Si Valor(P)=W
Terminar “Éxito: P es el vértice que contiene el dato W”
Paso 3 Continuar
Si W>Valor(P)
P=D(P)
En caso contrario
P=I(P)
Ir al paso 2.
5.4 ALGORITMO DEL CAMINO MÁS CORTO
En el ejemplo 5.2.2 se muestra que, en un grafo se pueden tener varios caminos entre dos
vértices, y la pregunta que surge es ¿cuál de todos los caminos es la ruta más corta?
Para responder esta pregunta, estudiaremos el algoritmo del camino más corto. Para ello
veamos primero algunas definiciones importantes.
Definición 5.4.1 (Grafo ponderado o con peso)

Un grafo ponderado es un grafo en el cual hay datos asociados a sus lados. Al lado (i, j) se
le asocia el valor w(i, j) el cual representa el peso del lado (i, j).
Por ejemplo, si en un sistema eléctrico se interpretan las conexiones como vértices y los
cables conectados como lados, al asignarle longitud a los cables se tiene un grafo ponderado. Con
frecuencia los pesos se usan para representar costos, en el ejemplo anterior los pesos podrían
representar el costo del cable entre dos conexiones.
Definición 5.4.2 (Peso o ponderación de un grafo)

La ponderación de un grafo es la suma de los pesos de los lados.
El peso de un camino se conoce como longitud del camino. Con frecuencia, el objetivo es
encontrar, en grafos ponderados, el camino más corto entre dos vértices dados, es decir, un
camino cuya longitud sea mínima.
El siguiente algoritmo permite encontrar la longitud del camino más corto.

El algoritmo de Dijkstra supone que se le han asignado marcas a los vértices del grafo
dado. Sea L(v) la marca del vértice v. Inicialmente todos los vértices tienen marcas temporales.
Cada iteración del algoritmo cambia el estado de una marca de temporal a permanente. Para
ilustrar el algoritmo se encierra en un círculo cada vértice que tenga marca permanente.
Algoritmo 5.4.1 (Algoritmo del camino más corto)

Este algoritmo determina la longitud del camino más corto de un vértice v a un vértice w en
un grafo conexo y ponderado. El peso de un lado (i,j) es w(i,j)>0 y la marca del vértice x es L(x).
Al terminar L(w) es la longitud del camino más corto de v a w.
1) Inicialización:
L(v)=0
Para cada vértice x a, L(x)=
T=conjunto de vértices.
2) ¿Terminó?
Si w T
Ha terminado (“L(w) es la longitud del camino más corto de v a w”)
3) Continuar
Escoja y T, en donde L(y) tiene el valor mínimo
T=T–{y}
4) Revisar marcas
Para cada vértice x T, adyacente a y, L(x)=mín{L(x),L(y)+w(y,x)}
Ir al paso 2).
Ejemplo 5.4.1
Considere la fig. 5.4.1. Determin la longitud del camino más corto del vértice a al vértice e.
Fig. 5.4.1
Paso 1: Inicialización:
L(a)=0, Para cada vértice x a, L(x)=
T={a,b,c,d,e,f,g}
Fig. 5.4.2

Paso 2: ¿Terminó?
No, por que e T
Paso 3: Seguir
Se elige el vértice a, en donde L(a) tiene el valor mínimo.
T=T–{a}={a,b,c,d,e,f,g}–{a)={b,c,d,e,f,g}
Paso 4: Revisar marcas
Los vértices adyacentes al vértice a son: b y f.
L(b)=mín{L(b),L(a)+W(a,b)}=mín{ ,0+2}=2
L(f)=mín{L(f),L(a)+W(a,f)}=mín{ ,0+3}=3
Ir al paso 2)
Fig. 5.4.3
Paso 2: ¿Terminó?
No, por que e T
Paso 3: Seguir
Se elige el vértice b, en donde L(b) tiene el valor mínimo.
T=T–{b}={b,c,d,e,f,g}–{b)={c,d,e,f,g}
Los vértices adyacentes al vértice b son: c, d y e
L(c)=mín{L(c),L(b)+W(b,c)}=mín{ ,2+2}=4
L(d)=mín{L(d),L(b)+W(b,d)}=mín{ ,2+1}=3
L(e)=mín{L(e),L(b)+W(b,e)}=mín{ ,2+4}= 6
Ir al paso 2)
Fig. 5.4.4
Paso 2: ¿Terminó?
No, por que e T
Paso 3: Seguir
Se puede elegir el vértice d o el vértice f por que tienen el mismo valor, elegimos d
en donde L(d) tiene el valor mínimo.
T=T–{d}={c,d,e,f,g}–{f)={c,e,f,g}


Los vértices adyacentes al vértice d son c, g y e
L(c)=mín{L(c),L(d)+W(d,c)}=mín{4,3+1}=4.
L(g)=mín{L(g),L(d)+W(d,g)}=mín{ ,3+1}=4
L(e)=mín{L(e),L(d)+W(d,e)}=mín{6,3+3}=6
Ir al paso 2)
Fig. 5.4.5
Continuando con este proceso se tiene la siguiente secuencia de graficas:
Fig. 5.4.6 Fig. 5.4.7 Fig. 5.4.8
Cuando se ha terminado el proceso, el valor del vértice final del camino representa la
longitud del camino más corto. Para formar el camino se parte del vértice final y se leen los
vértices de donde provienen, en este caso, la longitud del camino más corto es 6; y el camino es:
(a,b,d,e) o bien (a,b,e).
Otra forma de determinar la longitud del camino más corto, este se presenta en el ejemplo
siguiente.
Ejemplo 5.4.2
Determinar la longitud del camino más corto del vértice a al vértice e del grafo de la figura
5.4.1. Este es el mismo grafo del ejemplo anterior, pero ilustraremos la determinación del camino
más corto con otro procedimiento.

1. Se construye una tabla en donde:

a) La primera columna representa el vértice inicial del camino o de la arista.
b) Las siguientes columnas representan los vértices del grafo.
c) Otra columna representa el vértice final de la arista o del camino.
d) La siguiente columna representa la arista de longitud mínima.
e) La última columna señala la longitud del camino que se va construyendo, esta coincide
con la longitud mínima.
Así el número de columnas es igual al número de vértices más 4.
El grafo tiene 7 vértices, luego la tabla tiene 7+4=11 columnas.
p a b c d e f g q pq Longitud
vértice vértice Arista de mínima
inicial final longitud mínima
2. En la segunda fila consideramos el vértice inicial del camino y su longitud hacia los otros
vértices, si no hay una arista entre el vértice inicial y el vértice considerado indicamos que
hay una longitud desconocida L.
a 2 L L L 3 L
Como el vértice inicial es a y no hay una arista de a hacia a (no se consideran los lazos), no
hay una longitud asociada hacia este vértice. Como los únicos vértices adyacentes a a son b y f
estos son los únicos que tiene una longitud asociada y en los otros vértices se tiene una cantidad
desconocida.
3. Elegimos la longitud más corta y agregamos en la columna de vértice final, el vértice con el
que se obtiene la longitud más corta.
4. En la columna de arista de longitud mínima se agrega la arista que nos da la longitud
mínima.
5. En la última columna consideramos la longitud elegida como mínima.

La longitud mínima (entre 2 y 3), es 2 por lo tanto: b constituye el vértice final, ab es la

arista de longitud mínima y la longitud mínima es 2, así la tabla queda.
P a b c d e f g q pq Longitud
a / 2 L L L 3 L b ab 2
6. En la segundas fila se pone como vértice inicial el vértice final de la primera fila y se
vuelve a aplicar el procedimiento (pasos 2–5), hasta obtener que, el vértice de la longitud
mínima de la arista coincide con el vértice final del camino solicitado.
7. Al determinar la longitud desde el nuevo vértice inicial hacia los otros vértices:
b) Ya no se toma el vértice que marca el inicio del camino, este ya se uso y desde el paso
anterior no se consideró.
c) La longitud desde el nuevo vértice inicial hacia él mismo no se considera porque no hay
una arista entre él mismo (lazo).
d) Al determinar la longitud hacia los otros vértices se considera una longitud inicial, esta
es la de la arista mínima y se suma a ella la longitud de la nueva arista considerada; si la
nueva cantidad es mayor a la anterior, esta se desprecia y se mantiene la anterior.
e) Si el nuevo vértice inicial y otro vértice no son adyacentes, entonces se conserva la
cantidad anterior, si no se tenía una cantidad anterior se presenta la misma longitud
desconocida L.
En el ejemplo, iniciamos ahora con el vértice b y examinamos la longitud hacia los demás
vértices; hacia c la arista vale 2, pero ya teníamos una longitud acumulada de 2, así el valor es 4;
hacia d la arista vale 1, con la acumulada el valor es de 3; hacia e vale 4 lo que da 6; hacia f no
hay arista por lo que se conserva la cantidad anterior; y hacia g no hay arista y no se tenía una
cantidad antes por lo que es una longitud desconocida L.
P a b c d e f g q pq Longitud
a / 2 L L L 3 L b ab 2
b / / 4 3 6 3 L
La longitud mínima es 3 y esta se presenta en d y en f, en este caso tomamos cualquiera de

ellas y continuamos con el procedimiento, generalmente se toma en orden alfabético. Así,
tomamos como vértice final a d. Esta longitud mínima se obtuvo de la cantidad acumulada y de la
arista bd por lo tanto la arista que da la longitud mínima es ésta.

a / 2 L L L 3 L b ab 2
b / / 4 3 6 3 L d bd 3
El nuevo vértice inicial es d, repitamos el procedimiento.
a / 2 L L L 3 L b ab 2
b / / 4 3 6 3 L d bd 3
d / / 4 / 6 3 4
La longitud mínima es 3 se obtiene en el vértice f, sin embargo la arista no es la df porque

no existe, entonces regresamos sobre el vértice inicial hasta obtener la arista que nos dio esa
longitud; bf no es porque n o existe la arista, luego la única posibilidad es af la cual si es una
arista y tiene asociada una longitud de 3.
a / 2 L L L 3 L b ab 2
b / / 4 3 6 3 L d bd 3
d / / 4 / 6 3 4 f af 3
Ahora el nuevo vértice es f
a / 2 L L L 3 L b ab 2
b / / 4 3 6 3 L d bd 3
d / / 4 / 6 3 4 f af 3
5
f / / 4 / 6 / 4
Al determinar la longitud hacia los vértices que quedan, notamos que si hay una arista de f
a g, sin embargo al considerar la cantidad acumulada, aquí obtenemos un 5 que es mayor que el 4
del paso anterior, así esta se desprecia y se considera el mismo 4.
La longitud mínima es 4 y esta se presenta en c y en g, tomemos el vértice c; la arista fc no

existe por lo que no es la de longitud mínima, tomemos entonces la arista dc la cual si nos
produce un 4 por lo tanto esta es la arista de longitud mínima.

a / 2 L L L 3 L b ab 2
b / / 4 3 6 3 L d bd 3
d / / 4 / 6 3 4 f af 3
5
f / / 4 / 6 / 4 c dc 4
Iniciemos con el vértice c
a / 2 L L L 3 L b ab 2
b / / 4 3 6 3 L d bd 3
d / / 4 / 6 3 4 f af 3
5
f / / 4 / 6 / 4 c dc 4
6
c / / / / 6 / 4
La arista de longitud mínima no es cg ya que marcamos que esta llevaba a un 6, tampoco lo

es fg esta lleva a 5, luego la arista es dg.

a / 2 L L L 3 L b ab 2
b / / 4 3 6 3 L d bd 3
d / / 4 / 6 3 4 f af 3
5
f / / 4 / 6 / 4 c dc 4
6
c / / / / 6 / 4 g dg 4
El nuevo vértice inicial es g.
a / 2 L L L 3 L b ab 2
b / / 4 3 6 3 L d bd 3
d / / 4 / 6 3 4 f af 3
5
f / / 4 / 6 / 4 c dc 4
6
c / / / / 6 / 4 g dg 4
8
g / / / / 6 / /
La longitud mínima se obtiene en e, que era el vértice señalado como final, cuando se
encuentra este en el procedimiento se finaliza el proceso se hayan considerado todos los vértice
como aquí o no.
La arista de longitud mínima no es ge, vale 8; no es ce, no hay una arista; no es fe no hay
una arista; con de si hay una arista y esta vale 6; luego la arista de longitud mínima es de.
a / 2 L L L 3 L b ab 2
b / / 4 3 6 3 L d bd 3
d / / 4 / 6 3 4 f af 3
5
f / / 4 / 6 / 4 c dc 4
6
c / / / / 6 / 4 g dg 4
8
g / / / / 6 / / e de 6
8) Para determinar el camino de longitud mínima, representamos el árbol con raíz a y con las
aristas dadas en la columna de longitud mínima.

9) El camino de longitud mínima queda determinado por el camino en el árbol que va desde el
vértice inicial al vértice final.
El camino más corto es: (a,b,d,e) y su longitud es 6 (resultado del procedimiento o suma de
las aristas)
5.1. Isomorfismos de grafos
Definición 5.5.1 (Grafos Isomorfos)

Los grafos G 1 y G 2 son isomorfos si existe una función biyectiva f entre los vértices de
G 1 y G 2 y una función biyectiva g entre los lados de G 1 y G 2 , tales que un lado e es incidente a
v y w en G 1 si y sólo si el lado g(e) es incidente a los vértices f(v) y f(w) en G 2 . al par de
funciones f y g se les denominan isomorfismos.
Ejemplo 5.5.1
Determine si los grafos G 1 y G 2 son isomorfos.
Fig. 5.5.1
Solución
Sean f(a)=A, f(b)=B, f(c)=C, f(d)=D, f(e)=E y g(xi)=yi para i=1, …, 5.

La función f asocia a los vértices de G 1 y G 2 .

La función g asocia a los lados de G 1 y G 2 de manera que se preserve la incidencia.
Por lo tanto los grafos son isomorfos.
Teorema 5.5.1
Los grafos G1 y G2 son isomorfos si y sólo si para alguna ordenación de los vértices y
aristas sus matrices incidencia son iguales.
Ejemplo 5.5.2
Considere los grafos del ejemplo 5.5.1. Sus matrices de incidencia son:
x1 x2 x3 x4 x5 y1 y2 y3 y4 y5
a 1 1 0 0 0 A 1 1 0 0 0
b 0 1 1 0 0 B 0 1 1 0 0
c 0 0 1 1 0 C 0 0 1 1 0
d 0 0 0 1 1 D 0 0 0 1 1
e 1 0 0 0 1 E 1 0 0 0 1
Matriz de incidencia de G1 Matriz de incidencia de G2 .
Por lo tanto, de acuerdo al teorema anterior los grafos G 1 y G2 son isomorfos.
Ejemplo 5.5.3
Determine si los siguientes grafos son isomorfos.
Fig. 5.5.2
Solución
No son isomorfos por que el grafo G 1 tiene 6 vértices y el grafo G2 tiene 5 vértices.
Ejemplo 5.5.4
Fig. 5.5.3

Solución
No son isomorfos por que el grafo G 1 tiene 10 lados y el grafo G2 tiene 8 lados.
Una forma de mostrar que dos grafos G 1 y G 2 no son isomorfos es encontrar una
propiedad que se preserve en grafos isomorfos, pero no entre G 1 y G 2 . Una propiedad que se
preserva entre grafos isomorfos se llama invariante.
Invariantes
a) Igual números de vértices.
b) Igual número de lados.
c) Si G1 tiene m vértices de grado k, G2 también debe de tener m vértices de grado k.
d) Si en G1 hay un ciclo de longitud n, también debe de haberlo en G2.
Ejemplo 5.5.5
Fig. 5.5.4
Solución
a) G1 tiene 6 vértices y G2 tiene 6 vértices.
b) G1 tiene 9 lados y G2 tiene 9 lados.
c) G1 tiene 2 vértices de grado 2 y G 2 tiene 3 vértices de grado 2.
Por lo tanto los grafos G1 y G2 no son isomorfos.
Ejemplo 5.5.6
Fig. 5.5.5
Solución
c) G1 tiene 8 vértices de grado 4 y G 2 tiene 8 vértices de grado 4.
d) G2 tiene un circuito de longitud 3, y todos los circuitos de G 1 tienen, por lo menos, longitud
4.
Por lo tanto los grafos G1 y G2 no son isomorfos.

Ejemplo 5.5.7
Fig. 5.5.6
Solución
c) G1 tiene 2 vértices de grado 2, y tres vértices de grafo 3; G 2 tiene 2 vértices de grado 2 y
tres vértices de grado 3.
d) G1 tienen tres circuitos de longitud 3, 2 circuitos de longitud 4 y circuito de longitud 5 y G 2
tiene los mismos circuitos.
Esto sugiere que los grafos pueden ser isomorfos y para verificarlo es necesario encontrar
las funciones f y g biyectivas.
Designemos por E1 a las aristas de grafo G1 y por E2 las aristas del grafo G2.
E1={ab,ad,be,bd,bc,ce,cd}
E2={AB,AD,AE,BE,CE,CD,DE}
Sea f: V1 V2 definida como sigue:

f(a)=C, f(b)=E, f(c)=A, f(d)=D, f(e)=B.
ab E1 y f(a)f(b)=CE E2.
ad E1 y f(a)f(d)=CD E 2.
be E1 y f(b)f(e)=EB E2.
bd E1 y f(b)f(d)=ED E2.
bc E1 y f(b)f(c)=EA E2.
ce E1 y f(c)f(e)=AB E2.
cd E1 y f(c)f(d)=AD E 2.
Por lo tanto los grafos G1 y G2 son isomorfos.
5.6 Grafos planos
Definición 5.6.1 (Grafos planos)

Un grafo es plano si puede trazarse en un plano sin que se crucen sus aristas.
Ejemplo 5.6.1
El grafo de la figura 5.6.1 es plano por que puede reescribirse sin que se crucen sus lados,
ver fig. 5.6.2.
Fig. 5.6.1 Fig. 5.6.2
Si un grafo plano y conexo se representa en un plano, este queda dividido en regiones

contiguas llamadas caras. Una cara se puede representar por el circuito que forma su frontera.
Para el grafo de la figura 5.6.2, el circuito (1,2,4,1) representa la cara A, el circuito

(1,3,5,4,1) representa la cara B, el circuito ( 2,4,5,6,2) representa la cara C y el circuito
(1,2,6,5,3,1) representa la frontera de la cara D.
En 1752 Euler probó que para cualquier grafo plano y conexo, hay una relación entre el
número de caras, vértices y aristas, esto es, si f representa el número de caras, e el número de
lados y v el número de vértices se satisfacen la ecuación
f=e–v+2 (5.6.1)
Para el grafo de la figura 5.6.2, se tiene que f=4, e=8, v=6 y 4=8–6+2.
Ejemplo 5.6.2
Demostrar que el grafo K3,3 (ver fig. 5.6.3) no es plano.
Fig. 5.6.3 K3,3
Demostración
Supóngase que el grafo K3,3 es plano, esto implica que debe satisfacer la fórmula de Euler,
f=e–v+2.
Como cada circuito tiene, por lo menos, cuatro lados, cada cara está limitada, al menos, por
cuatro aristas, esto significa que, el número de aristas que limitan las caras es, al menos, 4f. En un
grafo plano cada arista es frontera de, a lo más, dos circuitos. En consecuencia,

2e 4f o bien 2e 4(e–v+2) (5.6.2)
Para el grafo de la figura 5.6.3, se tiene que e=9 y v=6, sustituyendo estos valores en la
expresión (5.6.2) se tiene que 18 4(9–6+2)=20.
Esto es una contradicción, esta contradicción se tiene por el hecho de haber supuesto que el
grafo K3,3 era plano. Por lo tanto que concluye que el grafo K3,3 no es plano.
Una demostración semejante se realiza para demostrar que el grafo K5 no es plano.
Definición 5.6.2 (Aristas en serie)

Si un grafo G tiene un vértice de grado 2 y aristas (a,b) y (a,c), con b c, se dice que los
lados (a,b) y (a,c) están en serie.
La reducción de una serie consiste en eliminar el vértice a del grafo y remplazar las aristas
(a,b) y (a,c) por (b,c). El grafo resultante G’ se dice que se ha obtenido de G mediante reducción
de serie.
Ejemplo 5.6.3
En el grafo G de la figura 5.6.5, los lados (e,d) y (e,c) están en serie. El grafo G’ de la
figura 5.6.6 se obtiene de G mediante reducción de serie.
Fig. 5.6.4 Fig. 5.6.5
Definición 5.6.3 (grafos homeomorfos)

Dos grafos G1 y G2 son homeomorfos, si G 1 y G2 se pueden reducir a grafos isomorfos
después de una sucesión de reducciones de serie, o bien, G 1 y G2 son homeomorfos si G 1 se
puede reducir a G2 mediante una sucesión de reducciones de serie y viceversa.
Ejemplo 5.6.4
Los grafos G1 y G2 de la figura 5.6.7 son homeomorfos, dado que los dos se pueden reducir
al grafo G’ mediante una sucesión de reducciones de serie.

Fig. 5.6.6
Ejemplo 6.5.5
Los grafos G 1 y G 2 son homeomorfos por que el grafo G 1 se puede reducir al grafo G2
mediante una sucesión de reducciones de serie.
Fig. 5.6.7
El siguiente teorema proporciona una condición suficiente y necesaria para que un grafo
sea plano.
Teorema 5.6.1 (Teorema de Kuratowski)

Un grafo G es plano si y sólo si G no contiene un subgrafo homeomorfo a K 3,3 o bien a K5.
Ejemplo 5.6.6
Fig. 5.6.8
Demostrar usando el teorema de Kuratowski, que el grafo no es plano.
Solución
Observe que los vértices a, d y e tienen grado 4. En K3,3, todos los vértices tienen grado 3,
así que se eliminan los lados (a,d) y (e,c) de modo que todos los vértices tengan grado 3 (ver fig.
5.6.9).

Fig. 5.6.9
Observe que si se elimina un lado más, se originarán dos vértices de grafo 2 y podrán
realizarse dos reducciones en serie.
Empleando el método de ensayo y error, vemos que si se elimina el lado (c,f) y se realizan
las reducciones de serie correspondientes, se tiene una copia isomorfa a K 3,3 (ver fig. 5.6.10. Por
lo tanto el grafo de la fig. 5.6.8 no es plano, pues contiene un subgrafo homeomofo a K 3,3 y este
no es plano.
Fig. 5.6.10
Ejercicios: Unidad V
5.1 Sean V={a,b,c,d,e} y E={(a,a), (a,e), (b,a), (c,d), (c,e), (d,a), (d,b), (e,b)}.
Represente el grafo que determinan.
5.2 Sean V={1,2,3,4,5} y E={(1,2), (1,3), (1,5), (2,3), (3,1), (3,4), (4,1), (4,3), (5,2)}.
Represente el dgrafo que determinan.
5.3 Dibuje, si es posible, un grafo conexo con 5 aristas y 7 vértices o explique por que no existe
tal grafo.
5.4 Trace K5 y K6.
5.5 Trace
a) K2, 4
b) K3, 3
5.6 Determine el grado de entrada y de salida de cada vértice el grafo representado en el

ejercicio 5.2.
5.7 Escriba la matriz de adyacencia y de incidencia de los siguientes grafos.

a) b)

5.8 Esquematice el grafo representado por cada una de las matrices de adyacencia.
a) b)
a b c d e f a b c d e f
a 0 1 0 0 0 1 a 1 0 0 0 0 0
b 1 0 0 0 1 1 b 0 0 1 1 1 1
c 0 0 1 0 0 0 c 0 1 0 0 0 1
d 0 0 0 1 1 0 d 0 1 0 0 1 0
e 0 1 0 1 0 1 e 0 1 0 1 1 0
f 1 1 0 0 1 0 f 0 1 1 0 0 0
5.9 Esquematice el grafo representado por cada una de las matrices de incidencia.
a) b)
e1 e2 e3 e4 e5 e6 e7
e1 e2 e3 e4 e5 e6 e7
a 1 0 0 0 0 0 1
a 0 0 0 1 1 0 0
b 1 1 0 1 1 0 0
b 0 1 0 0 0 1 1
c 0 0 1 0 0 0 0
c 1 0 0 0 0 0 0
d 0 1 0 0 0 0 0
d 0 1 1 0 0 0 0
e 0 0 1 0 0 0 1
e 1 0 0 1 1 1 1
f 0 0 0 0 1 1 0
5.10 Determine el grado de cada vértice de los grafos representados en el ejercicio 5.7.
5.11 Escriba la matriz de incidencia y de adyacencia del grafo completo de 5 vértices, K 5.
5.12 Esquematice el grafo representado por una matriz de 7 7 tal que su ij–esimo elemento es
1 si i+1 divide a j+1, o si j+1 divide a i+1, en otro caso, su ij–ésimo elemento es 0.

5.13 Esquematice el grafo representado por una matriz de adyacencia de 7 7 tal que su ij–ésimo
elemento es 1 si i+1 divide a j+1, o si j+1 divide a i+1, en otro caso, su ij–ésimo elemento
es 0.
5.14 ¿Cómo debe ser el grafo si alguna fila de su matriz de incidencia está constituida sólo por
ceros.
5.15 ¿Cómo debe ser el grafo si alguna fila de su matriz de adyacencia está constituida sólo por
unos.
5.16 Para cada uno de los siguientes grafos responda las siguientes preguntas
a) ¿Es posible trazar el grafo comenzando y terminando en el mismo punto, sin levantar el
lápiz del papel, y sin pasar dos veces por el mismo lado? Justifique su respuesta.
b) ¿Es posible trazar el grafo sin levantar el lápiz del papel y sin pasar dos veces por el mismo
lado? Justifique su respuesta.
a) b)
c) d)
5.17 ¿Para qué valores de n el grafo k n tiene un circuito de Euler?
5.18 ¿Para qué valores de m y n Km,n tiene un circuito de Euler?
5.19 Determine cuales de los siguientes grafos contienen ciclos de Hamilton. Describa cada uno
de los ciclos hamiltonianos encontrados. Si algunos de los grafos no tienen tales ciclos,
justifíquelo.
a) b)

c) d)
5.20 Dé un ejemplo de un grafo que tenga un circuito de Euler pero no un ciclo Hamiltoniano.
5.21 Dé un ejemplo de un grafo que tenga un circuito de Euler que sea también un ciclo
hamiltoniano.
5.22 Dé un ejemplo de un circuito que de Euler y un ciclo hamiltoniano, diferentes entre sí.
5.23 Trace todos la árboles binarios completos distintos.

c) Con 3 vértices.
d) Con 4 vértices.
e) Con 7 vértices.

5.24 Considere el siguiente grafo
Los vértices representan oficinas.

Una arista une dos oficinas si éstas se comunican
directamente entre sí.
Nótese que dos oficinas se pueden comunicar
directamente o a través de las demás.
a) ¿Las oficinas se pueden comunicar entre sí aunque se eliminen algunas de las

comunicaciones directas?
b) ¿Cuál es el máximo número de comunicaciones directas que se pueden eliminar sin que se
interrumpa la comunicación entre todas las oficinas?
c) Muestre como seria el grafo si se elimina el máximo número de comunicaciones directas
sin que se interrumpa la comunicación entre todas las oficinas?
5.25 Considere el siguiente árbol
a) Encuentre los padres de i y de k.

b) Halle los hijos de b y j.
c) Obtenga los antepasados del y m
d) Encuentre los descendientes de c y de
d.
e) Determine los hermanos de d y de p.
f) Halle los vértices internos.
g) Encuentre los vértices internos.
h) Dibuje el subárbol con raíz en j.
i) Dibuje el árbol dado con raíz en j.
5.26 Dibuje, si es posible, el árbol que cumpla las propiedades dadas, o explique por qué no
existe tal árbol.
a) El grado de todos los vértices es 2.
b) Con 5 vértices que tengan grado 1, 1, 2, 2 y 4.
c) Con 4 vértices internos y 6 vértices terminales.
d) Binario Completo; con 4 vértices internos y 5 vértices terminales.
e) De altura 3 y nueve vértices terminales.
f) De altura 4 y nueve vértices terminales.
5.27 Coloque las palabras de la frase “Sólo los niños saben lo que quieren” en un árbol binario
de búsqueda de altura mínima.
5.28 Coloque las palabras de la frase “Todos los alumnos pueden aprender si se lo proponen” en
un árbol binario de búsqueda de altura mínima.

5.29 En el siguiente grafo determina el camino más corto entre:
a) ayf
b) ayh
c) aye
d) cyg
e) bei
5.30 En el siguiente grafo determina el camino más corto entre:
a) ayh
b) aei
c) ayj
d) bei
e) dyg
f) cei
5.31 Hallar la longitud más corta y el camino que determina ésta longitud entre los vértices
indicados.
a) f y c.
b) a y c
5.32 Hallar la longitud más corta y el camino que determina ésta longitud entre a y todos los
demás vértices.
5.33 Un grafo plano y conexo tiene nueve vértices que tienen grado 2, 2, 2, 3, 3, 3, 4, 4 y 5.
¿Cuántas artistas hay? ¿Cuántas caras hay?.
5.34 Determine si los grafos G1 y G2 son isomorfos. Si son isomorfos, halle las funciones
biyectivas f y g; en caso contrario, establezca una invariante, que los grafos no tengan en
común.

a) b)
c) d)
e) f)
g) h)

5.35 Cada uno de los grafos es plano. Vuélvalas a dibujar de manera que los lados no se crucen.
a) b) c)
5.36 Pruebe que cada uno de los grafos no es plano, encontrando un subgrafo homeomorfo a K 5
o bien a K3,3.
a) b)
5.37 Determine si los siguientes grafos son planos. En caso de serlo, trácelo de nuevo de modo
que sus lados no se crucen; en caso contrario halle un subgrafo homeomorfo a K 5 o bien a
K3,3.
a) b)
c) d)

Unidad VI: Álgebra booleana y circuitos combinatorios
6.1 Compuertas lógicas.

6.1.1 Compuerta AND.
6.1.2 Compuerta OR.
6.1.3 Compuerta NOT.
6.1.4 Compuerta NAND.
6.1.5 Compuerta NOR.
6.2 Álgebra Booleana.

6.2.1 Definición.
6.2.2 Álgebra de Boole bivalente.
6.2.3 Propiedades del álgebra booleana.
6.3 Funciones Booleanas.

6.3.1 Simplificación de Funciones Boleanas usando Álgebra Booleana.
6.3.2 Simplificación de funciones Booleanas usando mapas de Karnaugh.
6.1 COMPUERTAS LÓGICAS
En los sistemas digitales4 la información que se procesa por lo general se presenta en forma
binaria. Las cantidades binarias sólo utilizan dos dígitos y pueden representarse por medio de
cualquier dispositivo que solamente tenga dos estados de operación o posibles condiciones.
Por ejemplo, un interruptor sólo tiene dos estados: abierto o cerrado. Podemos hacer que un
interruptor abierto represente un cero binario (0) y que uno cerrado represente el uno binario (1).
Con esta asignación se puede representar cualquier número binario y los estados de los diversos
interruptores.
Fig. 6.1.1
Otro ejemplo es donde se utilizan perforaciones en papel para representar números binarios.
Una perforación es un 1 binario y la ausencia de una perforación es un 0 binario.
4
Los sistemas digitales son una combinación de dispositivos diseñados para manipular cantidades físicas o
información que estén presente en forma digital; esto es, que sólo puedan tomar valores discretos, por ejemplo las
computadoras y calculadoras digitales, los relojes digitales, los controladores de señales de tráfico, las máquinas de
escribir, etc.

Fig. 6.1.2
Hay muchos dispositivos que solamente tienen dos estados de operación o que pueden
operarse en dos condiciones extremas. Como por ejemplo: la bombilla eléctrica (encendido o
apagado), la cinta magnética (magnetizada o desmagnetizada), el diodo (conductor o no
conductor), el termostato (abierto o cerrado), la fotocelda (iluminada u oscura), etc.
En los sistemas electrónicos digitales, la información se representa por medio de voltajes (o

corrientes) que están presentes en las entradas o salidas de los diversos circuitos. Por lo general,
el 0 y el 1 binarios se representan con dos niveles de voltaje, debido a las variaciones del circuito,
el 0 y el 1 se representa por medio de intervalos de voltaje. Cuando este nivel de voltaje es bajo
(entre 0 y 0.8 voltios) representa un 0 y cuando el nivel de voltaje es alto ( entre 4 y 5 voltios)
representa un 1.
Cada carácter binario, cero o uno, recibe el nombre de bit, nombre que deriva de las dos
primeras y de la última letra de la expresión inglesa “binary digit”, que significa precisamente
dígito binario.
La forma en que un circuito digital responde a una entrada se conoce como lógica del
circuito. Cada tipo de circuito digital obedece a cierto conjunto de reglas lógicas.
El 0 lógico representa a: falso, desactivado, bajo, no, interruptor abierto, etc.

El 1 lógico representa a: verdadero, activado, alto, sí, interruptor cerrado, etc.
Circuitos combinatorios.
Los circuitos pueden ser combinatorios o secuenciales. Un circuito combinatorio no tiene
memoria, esto es, las salidas se determinan directamente de forma única en cualquier momento
de las combinaciones presentes de entrada sin tener en cuenta las entradas anteriores y el estado
del sistema.
Los circuitos para los cuales la salida es una función que depende de las entradas y del
estado del sistema, se llaman circuitos secuenciales.
Los circuitos combinatorios pueden construirse usando dispositivos de estado sólido,

llamados compuertas, que son capaces de hacer cambios de nivel en el voltaje (bits).
Las compuertas son circuitos que se emplean para combinar niveles lógicos digitales (unos y
ceros) en formas específicas. Las compuertas básicas son: AND, OR, NOT, NAND Y NOR.

6.1.1 Compuerta AND
Definición 6.1.1 (Compuerta AND)

En un circuito digital la compuerta AND es un circuito que tiene dos o más entradas donde
cada una de las entradas son bits. Si se tienen dos entradas x1 y x2, la compuerta AND de x1 y x2
que se denota por x1 x2 , tiene una salida ALTA (nivel lógico 1) si la entrada x1 y x2 están en un
nivel lógico 1. La salida de la compuerta AND será BAJA (nivel lógico 0) si alguna de sus
entradas está en nivel lógico 0, esto es
1 si x1 1 y x2 1
x1 x2
0 en otro caso.
Esta compuerta también puede darse a través de la siguiente tabla lógica.
x y x y
0 0 0
0 1 0
1 0 0
1 1 1
La compuerta AND se representa por
Fig. 6.1.3
Una compuerta AND de tres entradas produce una salida de lógica 1 si las tres señales de
entrada son de lógica 1. La salida produce una señal de lógica 0 si cualquier entrada es de lógica
0.
Los aspectos importantes que deben recordarse en relación a las compuertas AND son:
a) La compuerta AND se ejecuta exactamente igual que la multiplicación ordinaria de unos y

ceros.
b) Una salida igual a 1 ocurre sólo en el caso de que todas las entradas sean 1.
c) La salida es cero en cualquier caso donde una o más entradas sean 0.

6.1.2 Compuerta OR
Definición 6.1.2 (Compuerta OR)

En un circuito digital la compuerta OR es un circuito que tiene dos o más entradas donde
cada una de las entradas son bits. Si se tienen dos entradas x1 y x2, la compuerta OR de x1 y x2 que
se denota por x1 x2 , tiene una salida ALTA (nivel lógico 1) si la entrada x1, x2 o ambos están en
un nivel lógico 1. La salida de la compuerta OR será BAJA (nivel lógico 0) si todas sus entadas
están en nivel lógico 0, esto es
0 si x1 0 y x2 0
x1 x2
1 en otro caso.
x y x y
0 0 0
0 1 1
1 0 1
1 1 1
La compuerta OR se representa por
Fig. 6.1.4
Esta misma idea puede ampliarse a más de dos entradas. Por ejemplo una compuerta OR
de cuatro entradas produce una salida con lógica 1 cuando cualquier entrada es de lógica 1. Su
salida será de lógica 0 si todas las señales de entrada son de lógica 0.
Los aspectos importantes que deben recordarse en relación a las compuertas OR son:
a) La compuerta OR produce un resultado de 1 cuando cualquiera de las variables de entrada

es 1.
b) La compuerta OR genera un resultado de 0 solamente cuando todas las variables de

entrada son 0.
c) En la compuerta OR, 1 1 = 1, 1 1 1 = 1, etc.
En este libro sólo se usarán compuertas de dos entradas.

6.1.3 Compuerta NOT.
Definición 6.1.3 (Compuerta NOT o inversor)

En un circuito digital la compuerta NOT acepta una sola variable de entrada, su nivel lógico
de salida siempre es contrario al nivel lógico de esta entrada. por ejemplo, si se tiene la variable x,
NOT x, se denota por x , donde
1 si x 0
x
0 si x 1
x x
0 1
1 0
La compuerta NOT se representa por
Fig. 6.1.5
Ejemplo 6.1.1
Señales de entrada-salida para las compuertas AND, OR y NOT (BAJA indica lógica cero
y ALTA indica lógica 1).
Fig. 6.1.6

6.1.4 Compuerta NAND.
Definición6.1.4 (Compuerta NAND)

La compuerta NAND es un circuito que produce una salida BAJA (nivel lógico 0) sólo
cuando todas sus entradas son ALTAS (nivel lógico 1). NAND es la contracción de las palabras
inglesas “NOT” y “AND” y se define como :
x NAND y = x y
La tabla de verdad es:
x y x NAND y
0 0 1
0 1 1
1 0 1
1 1 0
La compuerta NAND se representa por
Fig. 6.1.7
6.1.5 Compuerta NOR
Definición 6.1.5 (Compuerta NOR)

La compuerta NOR es un circuito que produce una salida ALTA (nivel lógico 1) sólo cuando
todas sus entradas son BAJAS (nivel lógico 0). NOR es la contracción de las palabras inglesas
“NOT” y “OR” y se define como:
x NOR y = x y
La tabla de verdad es:
x y x NOR y
0 0 1
0 1 0
1 0 0
1 1 0
La compuerta NOR se representa por
Fig. 6.1.8

Ejemplo 6.1.2
Determinar la salida de cada circuito combinatorio
a)
Z A B A
b)
Z A (B C)
c)
Z A B A C
d)
Z A B C D B D

Propiedades de los circuitos combinatorios
Los operadores , , y definidos en Z2 = {0, 1,}cumplen las siguientes propiedades.
Propiedades asociativas:
A B C A B C
A B C A B C A, B, C Z2
Propiedades conmutativas:
A B B A
A B B A A, B Z2
Propiedades distributivas:
A B C A B A C
A B C A B A C A, B, C Z2
Propiedades de identidad:
A 0 A
A 1 A A Z2
Propiedades de complemento:
A A 1,
A A 0 A Z2
Propiedades de D´Morgan:
A B A B
A B A B A, B Z2
Las demostraciones de estas propiedades son considerando las tablas y todas las combinaciones
de 0 y 1.
Definición 6.1.6 (circuitos combinatorios equivalentes)

Decimos que dos circuitos combinatorios, cada uno con entradas x1 , ..., xn y una única
salida, son equivalentes, si, cada vez que los circuitos reciben las mismas entradas, producen las
mismas salidas.
Para determinar si dos circuitos son equivalentes se pueden usar dos métodos:
Método 1: Elaborar la tabla de verdad de los dos circuitos.
Método 2: Usar las propiedades de los circuitos.

Ejemplo 6.1.3
Determinar si los siguientes circuitos son equivalentes.
B C A A B C
Método 1:
A B C A B B C B C A
0 0 0 1 1 1 1
0 0 1 1 1 1 1
0 1 0 1 0 0 1
0 1 1 1 0 1 1
1 0 0 0 1 1 1
1 0 1 0 1 1 1
1 1 0 0 0 0 0
1 1 1 0 0 1 1
A B C A B A B A B C
0 0 0 0 1 1
0 0 1 0 1 1
0 1 0 0 1 1
0 1 1 0 1 1
1 0 0 0 1 1
1 0 1 0 1 1
1 1 0 1 0 0
1 1 1 1 0 1
Como las salidas de las tablas de verdad son iguales, los circuitos son equivalentes.
Método II:
B C A
B C A Propiedad asociativa.
B A C Propiedad conmutativa.
B A C Propiedad asociativa.
A B C Propiedad conmutativa.
A B C Propiedad de De Morgan.
Por lo tanto los circuitos son equivalentes.

6.4 ÁLGEBRA BOOLEANA
6.2.4 Definición.
El concepto de variable lógica fue introducido en 1850 a través del uso del álgebra
booleana. El álgebra booleana permite expresar situaciones, en forma de lenguaje matemático. La
lógica digital adquiere su dimensión práctica a través de las compuertas y se consolida como una
ciencia estructurada mediante el álgebra booleana. El método booleano permite fácilmente
representar, analizar y diseñar circuitos digitales. Sus principios teóricos fueron desarrollados por
el matemático ingles George Boole en su obra “Análisis matemático de la lógica" publicada en
1847. Sin embargo, sólo hasta 1938 se descubrió su real utilidad.
Con el advenimiento de los tubos de vacío, los transistores y los circuitos integrados y la
fabricación de compuertas, circuitos y sistemas digitales con estas tecnologías, el álgebra
booleana adquirió un papel determinante en el desarrollo de la electrónica digital moderna y sus
aplicaciones.
En 1954 George Boole introdujo un tratamiento sistemático de lógica y para ello desarrolló
un sistema algebraico que hoy en día llamamos álgebra de Boole. En 1904 E. V. Huntington
formuló los postulados para la definición formal del álgebra de Boole.
Definición6.2.1 (Álgebra Booleana)

Un álgebra Booleana es un sistema matemático formada por:
1) Un conjunto B, con al menos dos elementos.
2) Dos operaciones binarias, la suma (+) y el producto ( ), y una operación unaria, la
complementación, definidas para todos los elementos de B.
3) Un conjunto de axiomas o postulados.
4)
Postulados:
1) Cerradura
a) El conjunto B es cerrado bajo el operador +.
b) El conjunto B es cerrado bajo el operador .
2) Identidad
a) Existe un elemento de identidad con respecto a +, designado por 0.
x+0=0+x=x.
b) Existe un elemento de identidad con respecto a , designado por 1.
x 1=1 x=x.
3) Conmutativo
a) Conmutativo con respecto a +: x+y=y+x.
b) Conmutativo con respecto a : x y=y x.

4) Distributivo
a) es distributivo sobre +: x (y+z)=(x y)+(x z).
b) + es distributivo sobre : x+(y z)=(x+y) (x+z).
5) Complemento
Para todo x B, existe un elemento x B llamado el complemento de x o la negación de x,
tal que:
a) x+ x =1.
b) x x =0.
La definición de álgebra booleana no incluye el axioma de asociatividad de las operaciones

suma y producto, porque éste es deducible de los últimos cuatro postulados.
Por lo tanto, para todo x,y z B se cumple:

6) Asociativa
a) Asociativo con respecto a +: x+(y+z)=(x+y)+z=x+y+z.
b) Asociativo con respecto a : x (y z)=(x y) z=x y z.
Se pueden formar muchas álgebras de Boole dependiendo de la forma en que se elijan los
elementos de B y las reglas de operación.
Ejemplo 6.2.1
Verificar que el conjunto dado con las operaciones definidas es un álgebra booleana. Sea U
un conjunto Universal y sea S=P(U), el conjunto potencia de U, para el cual se define lo
siguiente:
a. Operación binaria suma, definida por X+Y=X Y.

b. Operación binaria multiplicación, definida por X Y = X Y.
c. Operación unaria complementación, definida por X X .
d. El conjunto vacío, , desempeña el papel de 0.
e. Y el conjunto universal U el de 1.
Solución
Para que esta estructura sea un álgebra booleana se debe cumplir:
Identidad Conmutativa
X =X. X Y=Y X.
X U=X. X Y=Y X.
Distributiva Inversas
X (Y Z)=(X Y) (X Z). X X =U.
X (Y Z)=(X Y) (X Z). X X= .
Como los elementos de S son conjuntos y estos cumplen con las propiedades de los
conjuntos que son las mismas que las propiedades del álgebra booleana, se tiene que
(S, , , , ,U) es un álgebra booleana.

Ejemplo 6.2.2
Sea S={1,2,4,8}. Definimos
x+y=mcm(x,y);
x y=mcd(x,y);
8
x
x
para x, y S. (Aquí mcm es el mínimo común múltiplo y mcd es el máximo común
divisor). Demostrar que (S,+, , ,1,8) no es un álgebra booleana. (1 representa el elemento
identidad respecto a la suma y 8 representa el elemento identidad respecto a la multiplicación).
Solución:
Sean x=2k, y=2 m y z=2 n, donde 0 k,m,n 3.
Para que sea un álgebra booleana debe cumplir
Cerradura
El conjunto S es cerrado bajo el operador +.
mcm(x,y)=mcm(2k,2s).
El mcm(2k,2 m) es el mímino de los múltiplos de 2 k y 2 m.
Múltiplos de 2k=2k, 22k, 32k,...
Múltiplos de 2 m=2m, 22 m, 32 m,...
Observe que el mínimo debe ser un elemento con potencia 2, así es mínimo es de la forma:
mcm(2k,2 m)=2t donde t=máx{k,m} por tanto, x+y S.
El conjunto S es cerrado bajo el operador .

ahora bien mcd((x,y) es el máximo de los divisores comunes de x=2k y y=2 m.
Divisores de 2k: 1,2,22, ...,2k donde 0 m 3.
Divisores de 2 m: 1,2,22 , ...,2 m donde 0 n 3.
Así el mcd es el máximo de los divisores comunes, el cual es de la forma:
mcd(2k ,2 m)=2s donde s=mín{k,m}, por tanto x y S.
De lo anterior podemos ver que.

mcm(2a,2b)=2c donde c=máx{a,b}
mcd(2a,2b)=2c donde c=mín{a,b}
Identidad conmutativa
mcm(x,1)=x. x+y=mcm(x,y)=mcm(x,y)=y+x.
mcd(x,8) =x. x y=mcd(x,y)=mcd(x,y)=y x.
Distributiva
x+(y z)=(x+y) (x+z), es decir,
mcm(x,mcd(y,z))=mcd(mcm(x,y),mcm(x+y)).
Analicemos la primera parte de la igualdad

mcm(x,mcd(y,z))
Ahora bien mcd((y,z) es el máximo de los divisores comunes de y=2m y z=2n.
Divisores de 2 m: 1,2,22 , ...,2 m donde 0 m 3.

Divisores de 2 n: 1,2,22, ...,2 n donde 0 n 3.
Así el mcd es el máximo de los divisores comunes, el cual es de la forma
2s donde s=mín{n,m}. Así mcd(2 m,2 n) = 2s.
mcm(x,mcd(y,z)=mcm(x,2s)=mcm(2k,2s).
El mcm(2k,2s) es el mímino de los múltiplos de 2 k y 2s.
Múltiplos de 2k=2k, 22k, 32k,...
Múltiplos de 2s=2s, 22s, 32s,...
Observe que el mínimo debe ser un elemento con potencia 2, así es mínimo es de la
forma: mcm(2k,2s)=2t donde t=máx{k,s}=máx{k,mín{m,n}}.
De lo anterior podemos ver que.

mcm(2a,2b)=2c donde c=máx{a,b}
mcd(2a,2b)=2c donde c=mín{a,b}
Analicemos la segunda parte de la igualdad

mcd(mcm(x,y),mcm(x+y))=mcd(mcm(2k,2 m),mcm(2k,2 n))
mcm(2k,2 m)=2p donde p=máx{k,m}
mcm(2k,2 n)=2q donde q=máx{k,n}
Ahora bien, mcd(mcm(2k,2 m),mcm(2k,2 n))=mcd(2p,2q) = 2s donde

s=mín{p,q}=mín{máx(k,m},máx{k,n}}.
Por último falta demostrar que 2t=2s, esto se cumple si y sólo si t=s.
Analicemos por casos, proponiendo valores para k.
Si k = 0, se tiene t=máx{0,mín{m,n}=mín{m,n} y
s=mín{máx{0,m},máx{0,n}}=mín{m,n} y de esto se tiene que t=s.
Si k=1 y m=0, t=máx{1,mín{0,n}=máx{1,0}=1, para toda n.
s=mín{máx{1,0},máx{1,n}}=mín{1,n}, se tienen dos casos
caso1: n 1, s=mín{1,n}=1,
caso 2: n<1 s=mín{1,1}=1 de esto se tiene que t=s.
Si k=1 y m=1,t=máx{1,mín{1,n} se tienen dos casos
Caso 1: n 1, t=máx{1,1}=1
Caso 2: n<1, t=máx{1,0}=1
s=mín{máx{1,1},máx{1,n}}=
caso1: n 1, s=mín{1,n}=1
caso 2: n<1 s=mín{1,1}=1

Continuando con este proceso probamos que s=t, por lo tanto la primera propiedad
distributiva se cumple. El procedimiento para demostrar la otra propiedad distributiva es similar,
y se deja como ejercicio.
Complemento
8
Debe cumplir que x+ x =1. Sin embargo, para x=4 tenemos x+ x =mcm(4, )=4. Por
4
lo tanto, (S, +, , , 1, 8) no es un álgebra booleana.
Cada axioma de la definición de álgebra booleana está dada en parejas. Cada una
puede obtenerse de la otra intercambiando + por y 0 por 1.
Definición 6.2.2 (Expresión dual)

Llamamos expresión dual de una expresión, aquella que se obtiene de expresión original
cambiando el + por , el por +, el 0 por 1 y el 1 por 0.
Ejemplo 6.2.3
Escribir la expresión dual de x+(y z)+ y
Solución
Expresión dual: x (y+z) y
El álgebra booleana se parece mucho al álgebra ordinaria en algunos aspectos, por lo que la
manipulación de ésta podría resultar fácil, sin embargo, se debe tener cuidado de no sustituir las
reglas del álgebra ordinaria donde no sean aplicables.
6.2.5 Álgebra de Boole bivalente
En particular se analizará un álgebra de Boole bivalente , es decir, una con dos elementos.
El álgebra de Boole bivalente tiene aplicaciones en la lógica de proposiciones. El interés de
estudiar álgebra booleana bivalente es su aplicación a los circuitos con compuertas.
Una álgebra de Boole bivalente se define:

1. Sobre un conjunto de dos elementos B={0,1}.
2. Dos operadores binarios definidos como:
a) Adición o suma lógica: también llamada operación OR. Esta operación corresponde a la
disyunción de proposiciones en lógica y a la unión de conjuntos, su símbolo es (+) y se
define como:

x y x+y
0 0 0
0 1 1
1 0 1
1 1 1
b) Multiplicación o producto lógico: Llamada también operación AND. Esta operación

corresponde a la conjunción de proposiciones en lógica y a la intersección de conjuntos;
su símbolo es ( ) y se define como:
X y xy
0 0 0
0 1 0
1 0 0
1 1 1
Un operador unario definido como:

Complementación o inversión lógica: Denominada también operación NOT. Este
operador corresponde a la negación de proposiciones en lógica y a la operación de
complementación en conjuntos. Se simboliza con apóstrofo o con una raya en la parte
superior de la variable complementada y se define como:
x x
0 1
1 0
3. Los postulados de Huntington son válidos para el conjuntos B={0,1} y para los operadores
definidos anteriormente. Como se muestra a continuación.
1. A partir de las tablas se observa que el conjunto es cerrado ya que el resultado de cada
operación es 1 ó 0 y 1, 0 B.
2. De las tablas se observa que:

a) 0+0=0 0+1=1+0=1.
b) 1 1=1 1 0=0 1=0.
Lo cual establece los dos elementos de identidad 0 para + y 1 para .
3. Las leyes conmutativas se observan en la simetría de las tablas de los operadores

binarios
4. La ley distributiva x (y+z)=(x y)+(x z), puede demostrase que es verdadera con la
siguiente tabla de verdad.
x y z y+z x (y+z) xy xz (x y)+(x z)

0 0 0 0 0 0 0 0

0 0 1 1 0 0 0 0
0 1 0 1 0 0 0 0
0 1 1 1 0 0 0 0
1 0 0 0 0 0 0 0
1 0 1 1 1 0 1 1
1 1 0 1 1 1 0 1
1 1 1 1 1 1 1 1
La ley distributiva de + sobre se demuestra de la misma forma.
5. De la tabla de complementos se demuestra que:

a) x+ x =1 ya que 0+ 0 =0+1=1 y 1+1 =1+0=1.
b) x x =0, ya que 0 0 =0 1=0 y 1 1 =1 0=0.
Nota: para representar x y se usará la notación xy.
Teorema 6.2.1
En un álgebra booleana el complemento de la variable x, x es único, es decir que si x+y=1
y x y=0 entonces y= x .
Demostración:
y=y(1)
=y(x+ x )
=yx+y x =0+y x =x x +y x = x (x+y)= x 1= x
El álgebra booleana se utiliza para describir los efectos que producen las entradas lógicas
sobre los diversos circuitos digitales (circuitos lógicos). También se usa para manipular variables
lógicas en la determinación del método de ejecución de una cierta función de circuito.
6.2.6 Propiedades del álgebra booleana.
1) Idempotencia 4) Complemento o involución

a) x+x=x b) x =x
b) x x=x
5) De Morgan
2) Dominación o acotación a) x y x y
b) x+1=1
c) x 0=0 b) x y x y
3) Absorción 6) Asociativa
a) x+x y=x a) x+(y+z)=(x+y)+z=x+y+z.
b) x (x+y)=x b) x (y z)=(x y) z=x y z.

Unidad I: Introducción a la lógica Cálculo proposicional
Demostración de propiedades
Propiedad de idempotencia
a) Demuestre que x+x=x
x+x=(x+x) 1 Identidad
=(x+x)(x+ x ) Inversos
=x+x x Distributiva
=x+0 Inversos
=x Identidad
b) Demuestre que x x=x

x=xx+0 Identidad
=xx+x x Inversos
=x(x+ x ) Distributiva
=x 1 Inversos
=x Identidad
Propiedad de dominación
a) Demuestre que x+1=1
x+1=1 (x+1) Identidad
=(x+ x )(x+1) Inversos
=x+( x 1) Distributiva
=x+ x Identidad
=1 Complemento
b) Demuestre que x 0=0

x 0=x 0+0 Identidad
=x 0+x x Inversos
=x(0+ x ) Distributiva
=x x Identidad
0 Inverso
Propiedad distributiva
a) Demuestre que x+xy=x
x+xy=x 1+xy
=x (1+y)
=x(y+1)
=x 1=x
b) Demuestre que x(x+y)=x

x(x+y)=(x+0)(x+y)
=x+(0 y)
=x+0=x

Propiedad de involución o complemento

Demostrar que x x
Sabemos por el postulado 5 que x+ x =1 y x x =0 lo cual define el complemento de x. Por
lo que el complemento de x es x y es también x . Dado que el complemento es único se tiene
que x x.
Propiedad de De Morgan
a) Demuestre que x y x y
Sabemos que x y (x y) =0 y si x y x y se debe cumplir que:
( x y)( x y) 0 y (x y) ( x y) 1.
( x y)( x y) ( x y) x ( x y) y
= ( xx ) y x( y y )
=0 y x 0
=0+0
=0
(x y) ( x y) = ( x y) x x y y
= x x y x y y
= (1 y )( x 1)
=(1)(1)
=1
b) La demostración de x y x y se tiene por dualidad.
Las propiedades del álgebra de Boole pueden demostrarse también por tablas de verdad. En
estas tablas, ambos lados de la relación tienen resultados idénticos para todos los valores posibles
de las variables integrantes.
Para evaluar las expresiones de Boole se deben tener en cuenta las siguientes prioridades:
1. Paréntesis.
2. Operador NOT.
3. Operador AND.
4. Operador OR.
Esto es, los paréntesis deben ser evaluados antes que otras operaciones, después el
complemento, luego la AND y por último la OR.
Ejemplo 6.2.4
Dado que A=1, B=0 y C=1, evalúe las siguientes expresiones:

a) (A+B) (C+ A )=(1+0)(1+0)=(1) (1)=1

b) ( B AC A) C ) = (1+ 1(0) 1 0 ) = (1+ 0 1 0 )=1+0+0=1
6.5 FUNCIONES BOOLEANAS
6.3.3 Simplificación de Funciones Booleanas usando Álgebra Booleana.
Una expresión para un circuito lógico, puede reducirse a una forma más simple que
contenga menos términos o variables en uno o más términos. La nueva expresión puede utilizarse
para implantar un circuito que sea equivalente al original pero que contenga menos compuertas y
conexiones.
Ejemplo 6.3.1
considere los siguientes circuitos:
Fig. 6.3.1
La tabla de verdad de cada circuito se describen a continuación:
A B C A B A B AC A B AC (B + C) A( B C )
0 0 0 1 1 0 0 0 0 0
0 0 1 1 1 0 1 1 1 1
0 1 0 1 0 1 0 1 1 1
0 1 1 1 0 1 1 1 1 1
1 0 0 0 1 0 0 0 0 0
1 0 1 0 1 0 0 0 1 0
1 1 0 0 0 0 0 0 1 0
1 1 1 0 0 0 0 0 1 0
Observe que las columnas 8 y 10 son iguales esto significa que los circuitos producen la
misma salida, cuando esto sucede se dice que los circuitos son equivalentes, ya que ambos
circuitos ejecutan la misma lógica, debe ser obvio que el circuito más simple resultará más viable
debido a que contiene menos compuertas y, por tanto, será más pequeño y menos costoso que el
original.
Además la confiabilidad del circuito mejorará por que hay menos interconexiones que
puedan llevar a fallas potenciales del circuito.

Definición 6.3.1 (Función booleana)

Es un conjunto finito de símbolos, cada uno representa una constante o una variable,
combinados mediante las operaciones de suma, producto o complementación. Por ejemplo, la
expresión x x , se puede representar como una función de una variable de la siguiente manera:
f ( x) x x y la expresión xy x y se puede representar como una función de dos variables
f ( x, y ) xy x y .
Para simplificar funciones usando álgebra booleana no hay una metodología que nos
indique que ley se debe aplicar en primer lugar, por lo que hay diversas formas para simplificar.
Ejemplo 6.3.2
Simplifique las siguientes expresiones usando el álgebra booleana.
a) f(x,y)=x+xy
Solución 1
El alumno puede observar que puede aplicar directamente la propiedad de absorción y
simplificar a x+xy=x.
Solución 2
El alumno puede aplicar la propiedad distributiva
x+xy=x(1+y) distributiva
=x 1 dominación o acotación
=x Identidad
b) f(x,y)=x( x y )
Solución
x ( x y ) =x x +xy Distributiva
=0+xy Complemento
=xy Identidad
c) f(x,y)=x+( x y)
Solución
x+( x y)=(x+ x )(x+y) Distributiva
=1(x+y) Complemento
=x+y Identidad
d) f(x,y,z)= x y z x yz
Solución
= x( y z yz ) Distributiva
= x z( y y) Distributiva
= x z.1= x.z Complemento e identidad.

e) f(A,B,C)= ABC AB A C
Solución
ABC A B A C = ABC AB A C De Morgan.
= ABC AB A C Involución.
= ABC A B A A BC Distributiva.
= ABC A B A BC Conmutativa e idempotencia.
= AC B B AB Conmutativa y distributiva.
AC (1) AB Complemento.
AC A B Identidad.
= A(C B) Distributiva.
f) f(A,B,C)= ABC ABC ABC

Solución 1
ABC ABC A BC = AB(C C ) ABC Distributiva.
= AB(1) ABC Complemento.
= AB A BC Identidad.
= A( B BC ) Distributiva.
= A( B C ) Por c).
Solución 2
Los dos primeros términos tienen a las variables AB en común. El primero y el último
tienen a las variables AC en común. ¿Cómo saber si debemos factorizar AB de los dos primeros
términos o bien AC del primero y el último?.
Se pueden hacer ambas cosas utilizando el término ABC dos veces. Esto es, se puede
reescribir la expresión agregando el término ABC. Esto es válido ya que ABC+ABC=ABC.
ABC ABC A BC = ABC ABC ABC ABC

= AB(C C ) AC ( B B)
= AB(1) AC (1) AB AC
g) f(x,y,z)=xy+ x z yz
Solución
xy+ x z yz =xy+ x z yz ( x x) =xy+ x z yzx yz x
= xy+(1+z)+ x z (1 z )
= xy.1+ x z.1
= xy+ x z

SIMPLIFICACIÓN DE CIRCUITOS
El álgebra de circuitos es un álgebra booleana, por tanto todos los resultados obtenidos
anteriormente serán válidos. En particular las reglas relativas a simplificación de funciones
booleanas se aplican en el álgebra de circuitos.
Un método general para simplificar un circuito consiste en encontrar primero la función

booleana que representa el circuito, luego simplificar la función y finalmente dibujar el circuito
de la función simplificada.
El álgebra booleana proporciona el método más compacto y conveniente de representar,

analizar y diseñar circuitos lógicos. Cuando se diseña un circuito por métodos booleanos, el
primer paso consiste generalmente en obtener su tabla de verdad de acuerdo con las condiciones
de entrada y de salida. A partir de esta tabla se deriva entonces una función booleana que se
simplifica y conduce al circuito lógico deseado El circuito obtenido por este método es el óptimo
porque requiere de un numero mínimo de compuertas para su realización. Esto reduce el costo, el
tamaño físico y el consumo de potencia del mismo y mejora su confiabilidad y velocidad. Todas
estas consideraciones son importantes cuando se diseñan circuitos digitales.
Una tabla de verdad es una manera conveniente de representar simbólicamente una función
lógica. Todas las posibles combinaciones de los valores de la variable de entrada se presentan en
una tabla y, para cada combinación única de entradas, los valores de la variable de salida se listan
en una columna separada asignada a cada una de las variables. De este modo, la tabla de verdad
constituye una especificación completa de la lógica combinacional que se va a diseñar. En
muchos casos, la construcción de una tabla de verdad a partir de la especificación del problema
puede ser muy difícil, por lo tanto, el proceso que se implante en lógica debe ser estudiado en
detalle, hasta que se comprendan sus características.
FORMA NORMAL DISYUNTIVA

Una expresión está escrita en Forma Normal Disyuntiva FND (suma de productos) si:
a) Está formada por dos o más términos AND (productos).
b) Cada término AND se opera con OR.
c) Cada variable aparece en forma complementada o no complementada.
d) Cada término consta de todas las variables y se llaman términos minimales o
mintérminos.
Ejemplo 6.3.3
Las expresiones dadas constan de variables A, B, y C.
a) La expresión ABC ABC está escrita en forma normal disyuntiva por que consta de dos
términos AND (productos) que se operan con OR. Cada término AND consta de todas las
variables que aparecen en forma complementada o no complementada.

b) La expresión AB ABC consta de dos términos AND (productos) que se operan con OR.
Cada término AND consta de variables que aparecen en forma complementada o no
complementada , pero el primer término no consta de todas las variables.
Cuando esto sucede dicho término se multiplica por 1 donde ese uno se expresa en términos
de la variable que falta, por ejemplo, en este caso, al primer término le falta la variable C,
entonces
AB=AB(1)=AB(C+ C )=ABC+AB C
Y ahora si, la expresión ABC+AB C + A BC está escrita en forma normal disyuntiva.
Pasos para llegar a la forma normal disyuntiva de una expresión booleana

1. Aplicar las leyes de De Morgan hasta que los complementos aparezcan aplicados a
variables individuales.
2. Aplicar la ley distributiva del producto sobre la suma para que la función este dada en
sumas de productos.
3. Si en algún término falta una variable, entonces puede ser multiplicada por 1, expresando el
uno en términos de la variable que falta, como por ejemplo x+ x =1.
4. Distribuir el producto sobre la suma y, simplificar usando idempotencia.
Ejemplo 6.3.4
Escribir x y xz x en FND.
Solución:
x y xz x x y xz x De Morgan
=( x + y )( x + z )+ x De Morgan
=( x +y)( x + z )+ x Complemento
=( x +y) x +( x +y) z + x Distributiva
= x  x + x y+ x z +y z + x Distributiva
= x + x y+ x z +y z + x Idempotencia
= x +y z Absorción e idempotencia.
= x (y+ y )(z+ z )+y z (x+ x ) Se multiplica por 1 cada término.
= x y z+ x y z + x y z+ x y z + xy z Distributiva.
Cualquier función booleana puede colocarse en forma normal disyuntiva en más de una
forma. Basta cambiar el número de variables.
Ejemplo 6.3.5
f(x,y)=xy es una función booleana en dos variables en FND. Si la multiplicamos por z+ z
(que es 1), obtenemos f(x,y)=xyz+xy z la cual es una función booleana en tres variables escrita en
FND.

Se considerará, a menos que se diga otra cosa, que la FND se refiere a aquella forma que
contiene el menor número posible de variables. Con esta excepción, se puede demostrar que la
FND de una función está determinada unívocamente por la función.

FORMA NORMAL CONJUNTIVA

Una expresión está escrita en Forma Normal Conjuntiva FNC (producto de sumas) si:
a) Está formada por dos o más términos OR (sumas).
b) Cada término OR se opera con AND.
c) Cada variable aparece en forma complementada o no complementada.
d) Cada término consta de todas las variables, los términos se llaman términos maximales o
maxtérminos.
Ejemplo 6.3.6
Las expresiones dadas constan de variables A, B, y C.
a) La expresión ( A B C )( A B C ) está escrita en forma normal conjuntiva completa por
que consta de dos OR (sumas) que se operan con AND. Cada término OR consta de todas
las variables que aparecen en forma complementada o no complementada.
b) La expresión ( A B)( A B C ) no está escrita en forma normal conjuntiva por que

aunque consta de dos términos OR (sumas) que se operan con AND y cada término OR
consta de variables que aparecen en forma complementada o no complementada, el primer
término no consta de todas las variables.
Cuando esto sucede a dicho término se le suma 0, donde ese cero se expresa en términos de la
variable que falta, por ejemplo, en este caso, al primer término le falta la variable C, entonces
A+B=(A+B)+0 =(A+B)+C C =(A+B+C)(A+B+ C )
Y ahora si, la expresión (A+B+C)(A+B+ C )( A +B+C) está escrita en forma normal
disyuntiva completa.
Pasos para llegar a la forma normal conjuntiva de una expresión booleana

1. Aplicar las leyes de De Morgan hasta que los complementos aparezcan aplicados a
variables individuales.
2. Aplicar la ley distributiva de la suma sobre el producto para que la función este dada en
productos de sumas.
3. Si en algún término falta una variable, entonces se le suma cero expresando el cero en
términos de la variable que falta, como por ejemplo x x =0.
4. Distribuir el producto sobre la suma y, simplificar usando idempotencia.
Ejemplo 6.3.7
Escribir x y xz x en FNC.
Solución
x y xz x = x y )( xz x De Morgan
=( x + y )( x + z )+ x De Morgan
=( x + y)( x + z )+ x Complemento
=( x + x +y)( x + x + z ) Distributiva
=( x +y)( x + z ) Idempotencia (simplificación)
=( x +y+ z z )( x + z +y y ) Sumar cero.

=( x +y+z)( x +y+ z )( x + y +z)( x + y + z ) Distributiva
DE LA FNC A LA FND
Para pasar de la forma normal conjuntiva a la disyuntiva o viceversa se aplican las
propiedades distributivas.
Ejemplo 6.3.8
a) Escribe la expresión (A+B)( A + B ) en forma normal disyuntiva.
(A+B)( A + B )=A( A + B )+B( A + B ) Distributiva
=A A +A B +B A +B B Distributiva
=0+A B +B A +0
=A B + A B FND
b) Escribe la expresión (A+B)(A+ B ) en forma normal disyuntiva.

(A+B)(A+ B )=A+(B B ) Distributiva
=A+0=A=A1=A(B+ B )=
AB+A B FND
Teorema 6.3.1
Dos expresiones booleanas son iguales si y sólo si sus respectivas FND (FNC) son iguales.
Teorema 6.3.2
Para establecer cualquier Identidad en álgebra booleana, es suficiente verificar el valor de
cada función para todas las combinaciones de 0 y 1 que pueden asignarse a las variables.
Deducción de funciones booleanas a partir de tablas de verdad
Para determinar la función en forma normal disyuntiva usando tablas de verdad se pueden
seguir los siguientes pasos:
1) Se eligen los renglones para los cuales la función vale 1.

2) Si a1, a2,... a n, representan los valores asignados a x1, x2,... xn, en ese orden, donde cada ai es
0 o 1, use xi , si ai=0, y xi, si ai=1 para cada xi, i=1,2,...,n.
3) Multiplique las variables correspondientes en cada renglón y después sume los términos de
los renglones elegidos.
El término así escogido es un producto de n unos, y por lo tanto, es 1. Todos los otros
términos contendrán por lo menos un factor 0, y en consecuencia, serán 0.
En el diseño de circuitos, esta es precisamente la manera como las funciones booleanas son
construidas. Si tal tabla ha sido dada, entonces la expresión booleana en FND puede escribirse
por inspección. A cada conjunto de condiciones para los cuales la expresión booleana sea 1,
corresponderá un término en la FND escogida. La suma de estos términos da la función aunque
no necesariamente en la forma más simple.

Ejemplo 6.3.9
Considere la siguiente tabla de verdad:
A B C D Y
0 0 0 0 0 0
1 0 0 0 1 0
2 0 0 1 0 0
3 0 0 1 1 0
4 0 1 0 0 0
5 0 1 0 1 0
6 0 1 1 0 0
7 0 1 1 1 1 Mintérmino Y7
8 1 0 0 0 0
9 1 0 0 1 0
10 1 0 1 0 0
12 1 1 0 0 0
15 1 1 1 1 0
A continuación se detallará la forma de obtener la ecuación lógica (función lógica) que la

describe o sintetiza. El primer paso es identificar las filas o combinaciones de entrada que
producen como resultado un 1 a la salida. En nuestro caso, esto es aplicable a las filas 7, 11, 13 y
14. A continuación, observamos en cada fila los valores que toma cada variable de entrada. Si
una variable determinada vale 0, la reemplazamos mentalmente por su complemento ( A, B, C, D )
Si la variable vale 1, la dejamos tal como estaba, es decir, sin negar (A, B, C, D). En la siguiente
figura se ilustra este paso:
A B C D Y
7 0 1 1 1 1
11 1 0 1 1 1
13 1 1 0 1 1
14 1 1 1 0 1
A B C D Y
7 A B C D 1
11 A B C D 1

13 A B C D 1
14 A B C D 1
Seguidamente, asignamos a la salida de cada fila una expresión booleana equivalente a la

operación AND de las variables de entrada representadas de esta forma. En la siguiente figura se
ilustra este paso:
A B C D Y=Y7+Y11+Y13+Y14
7 0 1 1 1 1
11 1 0 1 1 1
13 1 1 0 1 1
14 1 1 1 0 1
Cada una de estas ecuaciones es un mintérmino. por ejemplo, el mintérmino asociado a la
fila 13 es: Y13 = AB C D.
La ecuación final se obtiene realizando la operación OR de todos los mintérminos. En

nuestro caso: Y = Y7 + Y11+ Y13 + Y14.
Reemplazando cada mintérmino por su expresión booleana correspondiente, se obtiene la

ecuación solicitada:
Y= A BCD+A B CD+AB C D+ABC D .
Una de las propiedades de las operaciones booleanas es que hay más de una combinación
de ellas que da lugar al mismo resultado. En otras palabras, la misma operación lógica puede
implementarse mediante más de un circuito lógico. El objetivo principal de la simplificación de
los circuios lógicos es el de determinar la combinación de puertas lógicas que producirá el
resultado deseado empleando el mínimo número de puertas lógicas, esto permite que las
compuertas ocupen poco espacio sobre una pastilla (chip) de silicio. Esto reduce el costo y el
consumo de potencia eléctrica de los circuios lógicos, se incrementa la velocidad. Un segundo
objetivo que se persigue en ocasiones es el de realizar un circuito lógico empleando sólo
determinados tipos de puertas lógicas. La simplificación algebraica efectiva requiere habilidad y
experiencia y, para diseños lógicos complicado, la reducción óptima es tanto un arte como una
ciencia y a menudo se requiere de la utilización de un software poderoso para diseño asistido por
computador.
Ejemplo 6.3.10
Exprese en FND la función booleana especificada por la siguiente tabla.
RENGLÓN x y z f(x,y,z)
1 0 0 0 0
2 0 0 1 0
3 0 1 0 0

4 0 1 1 0
5 1 0 0 1
6 1 0 1 0
7 1 1 0 1
8 1 1 1 0
Solución
La función booleana escrita en FND tendrá dos términos, los cuales se obtienen de las filas
5 y 7 que es donde la función booleana vale 1.
f(x,y,z)=x y z +xy z Simplificando la función se tiene:

f(x,y,z)=x z (y+ y )=x z
Para determinar la función en forma normal conjuntiva usando tablas de verdad se pueden
seguir los siguientes pasos:
1) Se eligen los renglones para los cuales la función vale 0.

2) Si a1, a2,... a n, representan los valores asignados a x1, x2,... xn, en ese orden, donde cada ai es
0 o 1, use xi , si ai=1, y xi, si ai=0 para cada xi, i=1,2,...,n.
3) Sume las variables correspondientes en los renglones y después multiplique los términos de
los renglones elegidos.
El término así escogido es una suma de n ceros, y por lo tanto, es 0. Todos los otros
términos contendrán por lo menos un factor 1, y en consecuencia, serán 1.
Ejemplo 6.3.11
Exprese en FNC la función booleana especificada por la siguiente tabla.
x y z f (x,y,z)
0 0 0 1
0 0 1 0
0 1 0 1
0 1 1 1
1 0 0 1
1 0 1 0
1 1 0 1
1 1 1 1
Solución

La FNC tendrá 2 términos o factores y serán los correspondientes a las filas segunda y
sexta en las cuales la función es 0.
Esto es: f(x,y,z)=(x+y+ z ’)( x +y+ z ), simplificando se tiene f(x,y,z)=y+ z .
Ejemplo 6.3.12
Considere la función definida en el ejemplo 6.3.11
Exprese la función booleana en FNC
RENGLÓN x y z f(x,y,z)
1 0 0 0 0
2 0 0 1 0
3 0 1 0 0
4 0 1 1 0
5 1 0 0 1
6 1 0 1 0
7 1 1 0 1
8 1 1 1 0
La función booleana escrita en FNC tendrá seis términos, los cuales se obtienen de las filas
1,2,3,4 y 6 que es donde la función booleana vale 0.
f(x,y,z)=(x+y+z)(x+y+ z )(x+ y +z)(x+ y + z )( x +y+ z )( x + y + z )
Si en la tabla de verdad se tienen sólo unos se obtiene la forma normal disyuntiva

completa (FNDC).
Por ejemplo considere la tabla de verdad de dos variables

x y f
0 0 1
0 1 1
1 0 1
1 1 1
La FNDC es x y + x y+x y +xy.
La FNCC es (x+y)(x+ y )( x +y)( x + y )
El complemento de cualquier función booleana en la FND (FNC) contiene los términos de

la forma normal disyuntiva (conjuntiva) completa que faltan en la función dada.
Ejemplo 6.3.13
x Y f
0 0 1
0 1 0
1 0 0

1 1 1
El complemento de(x+ y )( x +y) es (x+y)( x + y ).
Ejemplo 6.3.14
Hallar el complemento de la función booleana dada en el ejemplo 6.3.10
a) En FND.
b) En FNC.
Solución
a) El complemento será entonces los términos que faltan, así
Si se considera la FND sin simplificar se tiene una función de tres variables dada por
f ( x, y, z ) xyz xyz x y z x yz x y z x yz x yz xyz .
Si se considera la FND simplificada se tiene una función de dos variables dada por
f ( x, y, z ) xz xz xz x z , simplificando se tiene
f ( x, y, z ) xz xz+ x (z+ z )=xz+ x =(x+ x )(z+ x )= x + z.
Observe que f ( x, y, z ) x +z es el resultado obtenido si hubiéramos utilizado las leyes de
De Morgan en la función f ( x, y, z ) xz .
b) f ( x, y, z ) (x y z )( x y z )( x y z )( x y z )( x y z )( x y z) =
(x y z )( x y z)
Generalmente la FNC es usada cuando el número de ceros es menor que el número de unos
en la columna f; y la FND es usada cuando el número de unos es menor que el número de ceros
en la columna f
6.3.4 Simplificación de funciones Booleanas usando mapas de Karnaugh.
Para la simplificación de funciones booleanas, además del álgebra booleana, usamos los
mapas de karnaugh.
Un mapa de Karnaugh o mapa K es una tabla de verdad modificada que se utiliza para
simplificar ecuaciones Booleanas y diseñar circuítos lógicos de manera sistemática. Los mapas K
aprovechan la capacidad del cerebro humano de trabajar mejor con patrones gráficos que con
ecuaciones y otras formas de expresión analítica.
Los mapas de Karnaugh son diagramas rectangulares que tienen 2 n compartimentos, donde
n es el número de variables y cada compartimento representa una fila de la tabla de verdad. En
los mapas de Karnaugh se usa la FND como representación principal de una función. Cada
compartimento tiene un cero o un uno según corresponda al valor de la función.
Mapa K de dos variables.

Fig 6.3.2
En la figura siguiente (a), por ejemplo, se muestra una tabla de verdad de dos variables y en
las figuras (b) y (c) dos mapas de Karnaugh equivalentes. En los márgenes del mapa se señalizan
las coordenadas de cada uno de los cuadrados con respecto a la tabla de verdad.
Fig. 6.3.3
En el sistema de señalización de la figura (b) se utilizan las letras que identifican cada
variable para demarcar las zonas del mapa donde cada combinación vale 1 ó 0. En la figura (c),
las márgenes del mapa se señalizan con 0's y 1's, de tal forma que generan las coordenadas
exactas de cada una de las combinaciones de la tabla de verdad.
Llevar una tabla de verdad al mapa de Karnaugh es muy simple: se transcribe el valor de la
función lógica, para cada combinación de la tabla, a su correspondiente cuadrado, en el mapa,
según las coordenadas escogidas. Si se usa la convención de la figura (b), la tabla de la figura (a)
se lleva al mapa aplicando el siguiente razonamiento: la función lógica F, en la tabla, vale 1
cuando x=0 y y=0, o lo que es lo mismo, cuando x =1 y y =1. Este 1 lógico se ubicará, en el
mapa de Karnaugh, en el cuadrado situado en la intersección de las columnas x y y. Los otros tres
cuadrados deben estar ocupados por 0's, como lo indica la tabla de verdad.
Si se emplea el sistema de señalización de la figura (c), basta con ubicar las coordenadas
que correspondan a las combinaciones de la tabla de verdad y colocar, en los cuadrados, el valor
de la función lógica (0 ó 1). En este caso la función F(x,y)= x y .
Mapa K de tres variables.

Para tres variables (A, B y C) se requiere una tabla de verdad de ocho combinaciones. Por
tanto, el mapa de Karnaugh respectivo debe tener ocho compartimentos, como se muestra en la
figura siguiente.
Fig. 6.3.4

Mapa K de cuatro variables.

Un sistema lógico de 4 variables tiene 16 combinaciones posibles. Por esta razón, la tabla
de verdad debe tener 16 renglones y el mapa de Karnaugh 16 compartimentos, como se indica en
la figura siguiente.
Fig. 6.3.5
Mapa K de cinco variables.
Fig. 6.3.6
De la misma forma que una tabla de verdad, se lleva al mapa de Karnaugh una expresión
booleana se lleva a un mapa de Karnaugh. Se colocan 1's en los cuadrados donde los términos de
la ecuación valgan 1: el resto de los cuadrados se llenan con 0's o se dejan vacíos, que es lo más
usual. En la figura siguiente se muestran dos ejemplos ilustrativos.
Fig. 6.3.7

La figura (a) corresponde a una expresión booleana de tres variables que se lleva a un mapa
de Karnaugh. Con fines didácticos, se ha resaltado, con un bucle, el "grupo" de 1's que coloca, en
el mapa, cada uno de los términos de la expresión. Observe que el primer término de la función
representada en a) tiene una variable y esta corresponde a cuatro cuadros del mapa, esto es debido
a que cuando se representa la función en FND este término se transforma en cuatro términos. La
figura (b) presenta la misma situación usando una expresión booleana de cuatro variables (A, B,
C y D).
Los ejemplos de la figura anterior nos ofrecen una conclusión muy importante: el numero
de 1's que coloca, en una mapa de Karnaugh, cada uno de los términos que componen una
expresión booleana de N variables es igual a 2 N-n, siendo n el número de variables que utiliza el
término.
Por ejemplo, cuando se trabaja con tres variables (N=3) un término de una variable (n=1,
por ejemplo A o B).coloca en el mapa K 2 3-1=22=4 (cuatro) 1's, un término de dos variables (n=2,
por ejemplo AB o AC) coloca 2 3-2=21=2 (dos) 1's y un término de tres variables coloca un 1.
En este punto, es conveniente que nos preguntemos por que el mapa de Karnaugh facilita la
simplificación de expresiones booleanas. Responderemos esta inquietud usando un ejemplo.
Supongamos que se trata de simplificar la siguiente función lógica:
F ( A, B, C ) ABC ABC ABC ABC
La implementación directa de la expresión anterior requiere una compuerta OR de cuatro

entradas para sumar los 4 términos, 4 compuertas AND de tres entradas para producir cada
término y dos inversores para generar los complementos de B y C.
Utilizando las reglas del álgebra Booleana anteriormente estudiadas es posible simplificar
esta ecuación y minimizar el número de compuertas requeridas para su realización.
De a cuerdo a la ley distributiva

F ( A, B, C ) ABC ABC AB(C C ) AB(C C ) AB AB A( B B) A
Este resultado (F(A,B,C)=A) revela que la función original no requiere de compuerta

alguna para su realización: la salida es siempre igual a la entrada A, sin importar el estado de las
entradas B y C. En otras palabras, basta un cable conectado entre la entrada A y el punto al cual
va dirigida la función F.
La simplificación anterior es simple y sistemática por una sola razón: cada uno de los
términos de la expresión difiere del siguiente en el valor de una sola variable. Los términos que
difieren en una variable se pueden combinar y rechazar el término diferente. EI mapa de
Karnaugh nos permite visualizar este hecho con gran facilidad.
A los cuadrados o subrectángulos de un mapa de Karnaugh que difieren en una sola

variable o en un solo bit se les llama adyacentes, por ejemplo 001 y 011 son adyacentes por que

sólo hay un cambio de bit. Las reglas prácticas que se deben seguir para identificar adyacencias
en un mapa de Karnaugh son:
Cada subrectángulo del mapa de Karnaugh difiere de uno adyacente en una variable.
Para mapas de Karnaugh de dos variables, los subrectángulos cuyos lados horizontales o
verticales se tocan son adyacentes. Ver la siguiente figura.
Fig. 6.3.8
Para mapas de Karnaugh de 3 y 4 variables:

a) Los subrectángulos cuyos lados horizontales o verticales se tocan son adyacentes.
b) Los subrectángulos superiores e inferiores de una columna son adyacentes.
c) Los subrectángulos de los extremos derecho e izquierdo de una fila son adyacentes.
Fig. 6.3.9
El procedimiento sistemático que debe emplearse para simplificar una expresión Booleana
o una tabla de verdad mediante el mapa de Karnaugh se puede resumir en los siguientes pasos:
1) Llevar la tabla de verdad o la expresión Booleana a un mapa de Karnaugh.
2) Agrupar adyacencias de unos así:
a) Se hacen grupos de 1, 2, 4, 8, etc, compartimentos, esto es, el número de

compartimentos de un grupo debe ser de potencia de dos.
b) La agrupación de compartimentos (mintérminos) debe hacerse de forma tal que cada

uno esté incluido como mínimo una vez. Sin embargo, un compartimento puede
aparecer en distintas agrupaciones.
c) Las agrupaciones individuales deben seleccionarse de forma que comprendan el mayor

número de compartimentos con el fin de incluirlos en el mínimo de agrupaciones
posibles.

Para escribir la función simplificada la cual se va a expresar como una suma de términos, se
analizan los grupos para formar los términos. Estos términos se forman con la multiplicación de
las variables que no cambian en el grupo.
Ejemplo 6.3.15
Simplifique las siguientes funciones de Boole usando mapas K, exprese la solución usando
sólo compuertas NAN o NOR y dibuje el circuito de la función simplificada.
a) F ( x, y, z ) x yz x y z xyz xy z
Solución
La función está escrita en forma normal disyuntiva.
Fig. 6.3.10
F ( x, y, z ) yz xz
Para expresar la solución usando sólo compuertas NAND o NOR se toma el doble complemento
de la función la cual no se altera.
F( x, y , z ) yz xz yz x z

Circuito de la función simplificada
b) F ( A, B, C ) AC AB ABC BC
Solución
La función no está escrita en forma normal disyuntiva, por lo que en primer lugar debe
expresarse en esta forma.
F ( A, B, C ) AC ( B B) AB(C C ) ABC BC ( A A)
Fig. 6.3.11
F ( A, B, C ) C AB
F( A, B,C ) C AB C AB

Ejemplo 6.3.16
Simplifique las siguientes funciones de Boole usando mapas K.
a) F ( A, B, C ) 0,2,4,5,6
Solución
En este ejemplo se dan los mintérminos, que son los lugares del mapa donde la función vale
uno.
Fig. 6.3.12
F ( A, B, C ) 0,2,4,5,6 Z XY
b) F ( A, B, C, D) 0,1,2,4,5,6,8,9,12,13,14
Fig. 6.3.13
F ( A, B, C, D) 0,1,2,4,5,6,8,9,12,13,14 C AD B D
c) F ( A, B, C ) ABC BC D ABC D A BC
Solución
Fig. 6.3.14
F ( A, B, C ) ABC BC D ABC D ABC BD BC AC D

d) F ( A, B, C, D, E ) 0,2,4,6,9,11,13,15,17,21,25,27,29,31
Fig. 6.3.15
F ( A, B, C , D, E ) BE ADE AB E
Simplificación de un producto de sumas
Las funciones de Boole minimizadas, fueron expresadas en la forma de suma de productos,

los unos colocados en los cuadrados del mapa representan los términos mínimos de la función.
Los términos mínimos no incluidos en la función denotan el complemento de una función y se
representan en un mapa por cuadros no marcados por unos. Si se marcan los cuadros vacíos con
ceros y se combinan en cuadros adyacentes válidos, se obtiene una expresión simplificada del
complemento de la función, es decir F . El complemento de F dará de nuevo la función F.
Ejemplo 6.3.16
Simplificar la siguiente función F ( A, B; C, D) (0,1,2,5,8,9,10) en
a) Suma de productos.
b) Productos de sumas.
Los unos marcados en el mapa representan todos los términos mínimos (mintérminos) de la
función. Los cuadros marcados con ceros representan los términos mínimos no incluidos en F y
por tanto denotan el complemento de F.
Combinando los cuadrados con unos se obtendrá una función simplificada en suma de
productos: F ( A, B, C , D) B D BC ACD .
Si se agrupan los cuadrados marcados con ceros, se obtiene la siguiente función simplificada
F ( A, B, C , D) AB CD B D .
tomando el complemento de F , se obtiene una función simplificada en producto de sumas:
F ( A, B, C , D) ( A B)(C D) ( B D) .
Ejercicios: Unidad VI

6.1 Sea S={1,2,3,6}. Definimos

6
x+y=mcm(x, y); x y=mcd(x,y); x , para x, y S.
x
Aquí mcm es el mínimo común múltiplo y mcd es el máximo común divisor.
Demostrar que (S,+, , ,1, 6) es un álgebra booleana.
6.2 Para los siguientes enunciados expresar el enunciado dual correspondiente.

a. (x+y)(x+1)=x+xy+y.
b. x y =xy.
c. si x+y=x+z y x +y= x +z, entonces y=z.
d. x y =0 si y sólo si xy=x.
e. si x+y=0, entonces x=0=y.
f. x=0 si y sólo si y=x y + x y, para todo y.
g. x+x(y+1)=x.
6.3 Verificar los enunciados del ejercicio 6.2.
6.4 Dar el dual de A+ A B=A+B.
6.5 Demostrar los enunciados duales del ejercicio anterior 6.2.
6.6 Simplificar las siguientes funciones usando el álgebra booleana.

a) f(A,B,C)= AC ABD ABC D ABC
b) f(A,B,C) A B A B D D .
6.7 Diseñe un circuito lógico que tenga entradas A, B y C , y cuya salida sea alta cuando la
mayoría de las entradas sea alta.
6.8 Diseñar un circuito lógico de tres entradas, L, M y N, cuya salida sea alta cuando L=M=1 o
N=0.
6.9 Diseñar un circuito de 4 entradas que representan números binarios de 4 bits el cual
produce un salida alta sólo cuando el número binario es mayor que 0110 2=610.
6.10 Escribir la expresión en forma normal disyuntiva para un circuito con cuatro entradas y
cuya salida sea alta sólo cuando la primera entrada sea baja al mismo tiempo que la
segunda y tercer entrada sean bajas.
6.11 Realice el ejercicio anterior usando sólo compuertas NAND.
6.12 Multiplicar los siguientes términos suma para obtener una expresión suma de productos en
cada caso. Simplificar cuando sea posible.

a) (A+C)(B+D)
b) (A+C+D)(B+D+C)
c) (AB+C+DC)(AB+BC+D)
6.13 Escribir una expresión de Boole (en forma de suma de productos) para un circuito lógico
que tenga salida igual a 1 cuando A=1, B=0, C=0; A=1, B=1, C=0; A=1, B=1, C=1. La
salida debe ser 0 para cualquier otro caso. Simplificar la expresión obtenida y dibujar el
circuito.
6.14 Deducir la expresión booleana para un circuito lógico de compuertas que tiene una salida
igual a 0 sólo en los siguientes casos: A=1, B=1, C=1; A=0, B=0, C=0; A=1, B=0, C=0. La
salida será 1 en los demás casos.
6.15 Escribir las funciones F1, F2 y F3 en FND y FNC dadas en la siguiente tabla.
ENTRADAS SALIDAS
A B C F1 F2 F3
0 0 0 0 0 1
0 0 1 0 1 1
0 1 0 1 1 1
0 1 1 1 1 0
1 0 0 1 0 0
1 0 1 0 1 0
1 1 0 1 1 1
1 1 1 1 0 1
6.16 Escribir las funciones F1, F2 y F3 en FND y FNC dadas en la siguiente tabla. Dibujar el
circuito para las expresiones simplificadas.
ENTRADAS SALIDA
A B C Z
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 0
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 0

6.17 Escribir la expresión de Boole para F1, F2 y F3 de la siguiente tabla, en FNC y en FND,
simplificar cada expresión y dibujar el circuito lógico.
ENTRADAS SALIDAS
A B C F1 F2 F3
0 0 0 0 1 1
0 0 1 1 0 1
0 1 0 1 0 1
0 1 1 0 1 1
1 0 0 1 1 1
1 0 1 1 0 0
1 1 0 0 0 0
1 1 1 0 1 0
6.18 Expresar cada una de las siguientes funciones en FNDC en el menor número posible de
variables.
(u+v+w) uv uw
(x+y)(x+ y )( x + z )
xyz+(x+y)(xz)
6.19 Escribir la función de tres variables x, y, z en FND. Si la función vale 1 cuando x=1 ,
y=z=0.
6.20 Escribir la función de las tres variables x, y, z que vale 1 si x=y=1 y z=0 o si x=z=1 y=0 y
que vale 0 para los demás casos en FND y FNC.
6.21 A partir de la siguiente tabla de verificación, encuentra la expresión booleana

correspondiente en FND y en FNC.
x y z F(x,y,z)
0 0 0 1
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 0
1 1 1 1
6.22 Hallar el complemento de la FND del ejemplo anterior. Y simplificar si es posible.
6.23 Expresar en FND y FNC en el menor número de variables xyz+ x y u v +uv.

6.24 Encontrar el complemento de las siguientes funciones.

a) (x+y+z)( x + y + z ).
b) xy+ x y+ x y .
c) x z+x z xy+ x y+ x y .
6.25 Simplificar las siguientes expresiones usando los teoremas del álgebra booleana.
a) xy+(x+y) z +y.
b) x+y+ x y z .
c) yz+wx+z+wz(xy+wz).
d) xyz+ x yz+ x y z + x y z+x y z+x y z .
6.26 Hallar los complementos de las expresiones booleanas del ejercicio 6.25.
6.27 Hacer la tabla de verdad para las siguientes expresiones booleanas.

a) ABC A BC .
b) ABC A BC A BC .
c) A( BC BC ) .
d) ( A B)( A C )( A B) .
6.28 Usar el álgebra booleana para simplificar las siguientes expresiones y dibujar el circuito
para cada expresión, usando compuertas AND y OR.
a) A BC ABC ABC ABC .
b) ABC ABC ABC ABC ABC ABC ABC .
c) A( A B C )( A B C )( A B C )( A B C ) .
d) ( A B C )( A B C )( A B C )( A B C ) .
6.29 Usar el álgebra booleana para simplificar las expresiones dadas y dibujar el circuito lógico
de compuertas para las expresiones simplificadas, usando compuertas OR, AND y NOT.
a) ABC(AB C +A B C+ A BC).
b) AB+A B + A C+ A C .
c) AB+ABC+AB C +ACB.
d) AB( A B C +A B C + A B C ).
6.30 Expresar la solución del ejercicio 6.29 usando sólo compuertas NAND y NOR y hacer el
circuito combinatorio.
6.31 Simplificar las expresiones siguientes y dibujar el circuito lógico de compuertas de la

expresión simplificada usando compuertas AND, OR Y NOT.
a) A B C +AC+AB.
b) AC+AB+ A C .

6.32 Expresar la solución del ejercicio 6.31 usando sólo compuertas NAND y NOR y hacer el
circuito combinatorio.
6.33 Obtener el complemento de las siguientes expresiones. Por ejemplo, el complemento de

(AB+AC) es igual a AB AC =( A + B )( A + C )= A + B C .
a) (A+BC+AB).
b) (A+B)(B+C)(A+C).
c) AB+ B C+CD.
d) AB( C D+ B C).
e) A(B+C)( C + D ).
6.34 Complementar las siguientes expresiones.

a) A B +A B .
b) A B C+ A B .
c) A (B+ C ).
d) A(B C + B C ).
e) AB( B C+A C ).
f) AB+ A B (BC+ A B ).
6.35 Convertir las siguientes expresiones a la forma Normal Disyuntiva.

a) (A+B)( B +C)( A +C).
b) ( A +C)( A + B + C )(A+ B ).
c) (A+C)(A B +AC)( A C + B ).
6.36 Convertir las siguientes expresiones a la forma Normal Disyuntiva.

a) ( A + B )( C + B ).
b) A B( B C+ B C).
c) (A+B C )( A B + A B ).
d) AB(A B C + A C).
e) ( A + B)(A C + (B + C )).
f) ( A +C)(AB+AB+AC).
6.37 Multiplicar los siguientes términos suma para obtener una expresión suma de productos en
cada caso. Simplificar cuando sea posible.
a) (A+C)(B+D).
b) (A+C+D)(B+D+C).
c) (AB+C+DC)(AB+BC+D).
6.38 Escribir una expresión de Boole en FND para un circuito lógico que tenga salida igual a 1
cuando A=1, B=0, C=0; A=1, B=1, C=0; A=1, B=1, C=1. La salida debe ser 0 para cualquier
otro caso. Simplificar la expresión obtenida y dibujar el circuito.

6.39 Deducir la expresión booleana para un circuito lógico de compuertas que tiene una salida
igual a 0 sólo en los siguientes casos: A=1, B=1, C=1, A=0, B=0, C=0; A=1, B=0, C=0. La
salida será 1 en los demás casos.
6.40 En los siguientes ejercicios escribir las expresiones booleanas que representan los circuitos,
la tabla lógica y, simbólicamente, los datos de salida de cada compuerta.
a) b)
c) d)
6.41 Demostrar que los circuitos siguientes son equivalentes:

a)
b)
c)

d)
6.42 Simplificar las siguientes funciones usando mapas de Karnaugh. Expresar la solución en
FNC, en FND y Dibujar el circuito combinatorio de la función original y de la función
simplificada.
a) F ( A, B, C , D) D( A B) B(C AD) .
b) F ( K , L, M , N ) K LM K MN KLM N LM N .
c) F (W , X , Y , Z ) XZ W XY ( XY XY).
d) F ( w, x, y, z ) wx y x y z wxy z wx y .
e) F (w, x, y, z ) x yz x y z x y z x yz .
f) F ( A, B, C, D) ABC D AC D BC D ABCD BCD .
g) F ( A, B, C ) AC AB ABC BC .
h) F ( A, B, C, D) ABD AC D AB AC D AB D .
i) F (w, x, y, z ) xz wx y w( x y x y) .
j) F ( A, B, C, D) ( A B D)( A B D)(C D)(C D) .
k) F ( A, B, C, D) ( A C D) ( A B C )( A B D)( B C D) .
l) F ( x, y ) x y x y xy .
m) F ( x, y, z) x yz x y z x y z x yz .
n) F (w, x, y, z ) wx y x y z wxy z wx y .
o) F (w, x, y, z ) wx y w yz wx y z xy z .
6.43 Simplificar las siguientes funciones usando mapas de Karnaugh. Expresar la solución
usando sólo compuertas NAND o compuertas NOR y Dibujar el circuito combinatorio de la
función simplificada.
a) F ( A, B, C ) AC AB ABC BC .
b) F ( A, B, C, D) ABC BC D ABC D ABC .
c) F ( A, B, C, D) ABC D AC D BC D ABCD BCD .
d) F ( A, B, C, D) ( A B D)( A D)( A B D)( A B C D) .
e) F ( A, B, C, D) ( B D)( A C D)( A B C D)( A B C D) .
f) F (w, x, y, z ) (wz xyz )( y x yz) .

g) F ( w, x, y, z ) wx( yz y z ) wyz .
h) F ( w, x, y, z ) wx y yz wy z x y z .
i) F ( w, x, y, z ) ( w x y z )(( x y z )( w y z) .
FNC, en FND y Dibujar el circuito de la función simplificada.
a) F ( A, B, C) 0,2,4,5,6 .
b) F (w, x, y, z) 4,5,7,8,9,11 .
c) F (w, x, y, z) 0,1,2,3,8,9,10 .
d) F (w, x, y, z) 9,10,11,12,13 .
e) F (w, x, y, z) 3,4,5,7,9,13,14,15 .
f) F (w, x, y, z) 0,2,5,7,8,10,13,15 .
g) F (w, x, y, z) 5,6,8,11,12,13,14,15 .
h) F (w, x, y, z) 7,9,10,11,14,15 .
i) F ( A, B, C, D, E) 0,1,5,10,17,21,25,29 .
FNC, en FND y Dibujar el circuito combinatorio de la función simplificada.
a) F ( x, y, z ) 0,1,4,5 .
b) F ( w, x, y, z ) 1,3,5,7,13,15 .
c) F ( A, B, C , D) 0,1,2,3,4,10,11,15 .
d) F ( A, B, C , D) 3,4,6,7,9,10,11,15 .

Todo de Discretas

Uploaded by

Document Information

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

Todo de Discretas

Uploaded by

Copyright:

Available Formats

Unidad I: Introducción a la lógica Álgebra de proposiciones

LAS MATEMÁTICAS DE LA COMPUTACIÓN

UNIDAD I: INTRODUCCIÓN A LA LÓGICA

1.1 Conceptos y definiciones

1.2. Inferencia Lógica

1.3 Funciones lógicas y cuantificadores

1.1 CONCEPTOS Y DEFINICIONES

1.1.1 Cálculo proposicional

En el desarrollo de cualquier teoría, se hacen afirmaciones en forma de oraciones. Tales

Definición 1.1.1 (Proposición)

Una introducción a las matemáticas de la computación

Definición 1.1.2 (Valor de verdad)

b) Oraciones que no son proposiciones.

Una introducción a las matemáticas de la computación

como falsa o verdadera.

Oración Proposición (Si/No) Valor de verdad

1.1.2 Conectores lógicos

Las proposiciones pueden ser:

Definición 1.1.3 (Proposición simple)

Definición 1.1.4 (Proposición compuesta)

Una introducción a las matemáticas de la computación

La forma de las proposiciones compuestas depende del término de enlace utilizado, y no

Definición 1.1.5 (Conectivos lógicos)

Los valores de verdad de las proposiciones compuestas, pueden describirse mediante

Definición 1.1.6 (Tabla de verdad)

Definición 1.1.7 (Negación)

precediendo esta frase a la proposición p, o si es posible insertando en p la palabra no. La

Si el valor de verdad de una proposición p es verdadero (1), entonces el valor de verdad

Una introducción a las matemáticas de la computación

Como el valor de verdad de la proposición p es verdadero, p es falsa. En el lenguaje

Definición 1.1.8 (Conjunción)

Una introducción a las matemáticas de la computación

Si se conjuntan dos proposiciones que efectivamente sean verdaderas – ambas- se

Resumimos el valor de verdad de la conjunción de dos proposiciones en la siguiente

b) r: El basic es un lenguaje de programación

m n :Está lloviendo y hace sol.

Una introducción a las matemáticas de la computación

La disyunción puede ser inclusiva o exclusiva.

Definición 1.1.9 (Disyunción inclusiva)

En la siguiente tabla se resume el valor de verdad de la disyunción inclusiva de dos

Una introducción a las matemáticas de la computación

j l : Es falso que, 4 es par y 4 es primo. Verdadera

Definición 1.1.10 (Disyunción exclusiva)

La disyunción exclusiva de dos proposiciones es la relación que se establece entre dos

Nota 1.1.1: Usaremos la o acentuada (ó) para diferenciar la disyunción exclusiva de la

Una introducción a las matemáticas de la computación

Definición 1.1.11 (Implicación o condicional)

La proposición p también se llama hipótesis, antecedente o condición suficiente, y la

Consideremos un ejemplo de proposición condicional, y examinemos su valor de

Asignemos valor de verdad a las proposiciones.

1) Consideremos que p es falsa y q es falsa, y consideremos la proposición condicional con

2) Consideremos que p es falsa y q es verdadera, y consideremos la proposición

Una introducción a las matemáticas de la computación

En este caso no se ve claro el determinar un único valor de verdad a la proposición ya

3) Consideremos que p es verdadera y q es falsa, y consideremos la proposición

Si estudio, entonces no aprobaré.

4) Consideremos que p es verdadera y q es verdadera, y consideremos la proposición

En la siguiente tabla se resume el valor de verdad de la implicación entre dos

Para comprender el valor de verdad de la proposición condicional examinemos el

Asignemos valor de verdad a las proposiciones.

Una introducción a las matemáticas de la computación

La proposición p q es falsa ya que no se cumplió con la promesa de ir al cine si se

La proposición p q es verdadera ya que no se dijo ninguna mentira, no se tenía dinero

En el lenguaje común, lo usual es que la hipótesis y la conclusión de una proposición