II.

Conformal Mappings

Conformal Mappings
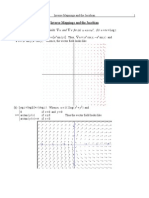
1. Sketch the families of level curves of u and v for the following functions f = u + iv. (a) f (z) = 1/z, (b) f z =1/ z 2 (c) f z =z 6 . Determine where f (z) is conformal and where it is not conformal. (a) First, 1/ z = respectively are
x y x y i 2 , so u= 2 2 and v= 2 . Thus, the contour maps for u and v 2 2 2 x y x y x y x y
2

Now, 1/z is analytic for all points in its domain. Since f ' z =1/ z 20 for any point in its domain, f is conformal on its domain. (b) First, 1/ z =
2

x 2 y 2 2 xy x 2 y 2 2 xy i 4 , so u= 4 and v= 4 . Thus, 4 2 2 4 2 2 4 2 2 4 x 2 x y y x 2 x y y x 2 x y y x 2 x 2 y 2 y 4

the contour maps are Again, 1/ z 2 is analytic and its derivative is non-zero on its domain, so 1/ z 2 is a conformal mapping on its domain.

II.6

Conformal Mappings

(c) We know that this function raises the modulus of each point to the sixth power and 6-tuples its argument. The contour maps are therefore a bunch of parallel lines. As above, the function is analytic and its derivative is equal to zero only at zero, so this function is conformal on {0}. 2. Sketch the families of level curves of u and v for f z =Log z=uiv. Relate your sketch to a figure in Section I.6. We see Log z=1/2 log x 2 y 2 i /2tan 1 x / y . Hence, the contour maps are

This looks similar to the figure on p. 23. 3. Sketch the families of level curves of u and v for the functions f =uiv given by (a) f z =e z , (b) f z =e z , where is complex. Determine where f (z) is conformal and where it is not conformal. (a) First, e z=e x cos yie x sin y . Thus, the contour maps are

Now, e z is analytic and its derivative is everywhere non-zero so it is a conformal mapping on .

II.6

Conformal Mappings

(b) First, e z=e aib xiy =cos bxay e axby i sin bxay eax by . Thus, the contour maps are

Since e z is analytic, it is conformal except if =0. 4. Find a conformal map of the horizontal strip {AIm z A} onto the right half-plane Re w0 . Adding A to each element of the set gives the new set {0<Im z <2 A}. There is a real B such that AB= i . Multiplying every element of the previous set by B gives {0<Im z <2 i}. The image of z e under this set gives the upper half-plane. Multiplying every element of the upper half-plane by i gives the right half-plane. Thus, sends {A<Im z< A} to the right half-plane. 5. Find a conformal map of the wedge {Barg z B} onto the right half-plane. Assume 0B . There is a real number A such that AB= /2 . Raising each element of {B<Arg z< B} to the Ath power gives the right half-plane. Thus, z A is the desired map. 6. Determine where the function f z =z 1/ z is conformal and where it is not conformal. Show that for each w, there are at most two values of z for which f z =w. Show that if r1 , f z maps the circle {z=r } onto an ellipse, and that f ( z ) maps the circle {z=1/r } to the same ellipse. Show that f z is one-to-one on the exterior domain D={z1}. Determine the image of D under f z . Sketch the images under f z of the circles {z=r } for r 1 , and sketch also the images of the parts of the rays {arg z= } lying in D. We see that f is differentiable on its domain {0}. Since f ' z =11/ z 2 , we see that f is conformal on {1} Suppose w= z1/ z . Then, z w=z 21 . This is a quadratic and has two solutions in the complex plane. Let z =r [cos +i sin ]. Then, f ( r [cos +i sin ])=r cos +ri sin +1/r cos 1/r sin =( r+1/ r) cos +i(r 1/r )sin which is the parametric equation of an ellipse with center at 0, major axis length 2(r + 1/r) coinciding with the real-axis, and minor axis length 2(r 1/r) coinciding with the imaginary axis. By the same token, f (1/ r [cos +i sin ])=(1/r +r )cos +i( 1/rr )sin =(1/ r+r )cos i( r1/ r)sin . This amounts to a reflection about the real axis, and so this set maps to the same ellipse.

II.6

Conformal Mappings

We have already determined that each circle of radius r centered at the origin gets mapped to the (unique) ellipse centered at 0 with major axis length 2(r +1/r) and minor axis length 2(r 1/r). Thus, the only possibility of a many-to-one mapping would be on a circle in the z-plane. Since each z in the domain is associated with a unique principal argument, we know that the function is 1-1 on the exterior of D. The image of D is the outside of the unit circle cos +i sin . (The ellipse centered at the origin with major axis length 2 and minor axis length 2.) To find the image of a ray, simply hold =const. and allow r to vary. The equation is then a hyperbola with the foci at . 7. For the function f ( z )= z+1/ z =u+iv , sketch the families of level curves of u and v. Determine the images under f (z) of the top half of the unit disk, the bottom half of the unit disk the part of the upper half-plane outside the unit disk, and the part of the lower half-plane below the unit disk. We see that f ( x+iy)=x+ that the level curves are: x y x y +i y 2 2 . Thus, u= x+ 2 2 and v = y 2 2 . We see 2 x +y x +y x +y x +y
2

for u and v respectively. We have already determined that circles of radius 1/r inside the unit circle get mapped to ellipses centered at the origin with foci (r + 1/r). The only new observation to note is that the top-half of the unit circle gets mapped to ellipses on the bottom half-plane and vice-versa. The outside behaves in the opposite way (that is, circles of radius r in the top-half of the unit circle get mapped to the upper half-plane).

II.6

Conformal Mappings

8. Consider f (z )= z+e i / z , where 0<< . Determine where f is conformal and where it is not conformal. Sketch the images under f (z) of the unit circle {z=1} and the intervals ( ,1 ] and [+1 , ) on the real axis. Show that w= f ( z) maps {z>1} conformally onto the complement of a slit in the w-plane. Sketch roughly the images of the segments of rays outside the unit circle {arg z= ,z1} under f (z). At what angles do they meet the slit, and what angles do they approach ? We see f ' ( z )=1ei / z 2 and so f is conformal except for when z 2=e i z =ei /2 . We see f (z )=ei / 2 (e i / 2 z+1/ei / 2 z ) . Thus, f is the composition of the function in Q7 and Q8 with a rotation of / 2. Now, the image of the unit circle is the limiting case of the family of circles {z=r | r>1}. Thus, the unit circle gets mapped to a degenerate ellipse of major axis length 4 and minor axis length 0. In other words, the unit circle gets mapped to the line segment [-2,2]. The function f (x )=x +1/ x is continuous on intervals not containing 0 in the sense of real variables, so f enjoys the intermediate value property. Thus, f [ 1, )=[ 2, ) and f ( ,1 ]=(,2 ] . Thus, the image of such sets under f (z) are the line segments above, rotated at an angle of / 2 about the origin. 9*. Let f = u + iv be a continuously differentiable complex-valued function on a domain D such that the Jacobian matrix of f does not vanish on any point of D. Show that if f maps orthogonal curves to orthogonal curves, then either f or f is analytic, with nonvanishing derivative. The back of the book has an explanation that I am not quite satisfied with, but I cannot as of yet supply my own solution.