JOMAR FAJARDO RABAJANTE MATH

235
2002-96301

1. The compartmental model that satisfies the system of differential equation is

βY r
bN

b b b

dYdtt=0=βX0Y0-b+rY0=Y0βX0-b+r>0 if X0>b+rβ (epidemic may happen)<0 if X0<b+rβ

no epidemic
Hence, the threshold population size is Nc=b+rβ .

If X0<Nc, then Y→0, i.e. the parasite cannot maintain itself in the population. So
based from the compartment model above if Y→0, then eventually there will be no
addition to [Z] so Z→0, i.e. infectives and the immune class will eventually die out.

It follows that the reciprocal of Nc, which we denote by σ=βb+r is the infection’s
contact rate. If X0=N, then the basic reproduction rate of infection R0= σN=βNb+r .

4. The given system of differential equation is consistent to the following

compartmental model which depicts the given situation:
v(t)
Since x and y are fractions of the whole hemophiliac population, then x+y=1. Since
all hemophiliacs were given infected blood at t=0, then this justifies the following
initial condition: x(0)=1 and y(0)=0.

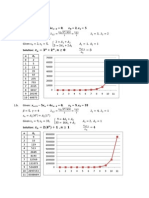
We can see in the following graphs that as v(t) increases faster than linearly, then
the fraction who are HIV positive but do not yet have AIDS, x, decreases faster
(converging to 0), and the fraction who have AIDS, y, increases faster (converging
to 1).

5. dTdt=s+pT1-TTmax-dTT-kVIT=0dT*dt=1-nrtkVIT-δT*=0dVIdt=1-npNδT*-
cVI=0dVNIdt=npNδT*-cVNI=0
VI=s+pT1-TTmax-dTTkT=skT+1kp1-TTmax-dTT=δT*1-nrtkVIT*=cVI1-npNδVNI=npNδT*c

VI=s+pT1-TTmax-dTTkT=skT+1kp1-TTmax-dTT=δcVI1-npNδ1-nrtkVI=c1-nrt1-
npNkT*=cVI1-npNδVNI=npNδcVI1-npNδc=npVI1-np